基于改进CORDIC算法的数字预失真实现

王 顶，刘太君，叶 焱

（宁波大学信息科学与工程学院，浙江宁波315211）

0 引言

在移动通信系统中，射频功率放大器（PA）作为移动通信系统中的重要组成部分，其效率和线性度影响着整个系统的性能。在4G系统中，提高功放效率的一种有效手段是采用Doherty技术，同时为了提高频谱利用率，广泛地采用了线性调制技术和多载波调制技术（如OFDM和CDMA），这样一来传输信号具有高宽带、高峰均值比（PAPR）和非恒定包络等特性，这些都需要PA具有高的线性度。数字预失真技术（DPD）的出现解决了功放的非线性失真问题，目前DPD大多采用基于QR分解的RLS算法的脉动阵列结构来实现。

QR分解有多种实现方式，其中Givens旋转由于具有并行性的优点应用于脉动阵列的设计中。然而传统的脉动阵列结构存在诸多问题:①Givens旋转单元存在平方根运算，在硬件实现时，平方根运算需要消耗大量的资源，且时间周期长;②对于通常采用多项式模型的功放来说，由于采用了N抽头和M阶的多项式，如果采用脉动阵列结构，其输入就有N×（M+1）项，这对于FPGA的资源是一个极大的挑战[1－4]。解决以上2个问题现有的方法是采用CORDIC算法，但正如文献[5]指出的，传统的CORDIC算法存在多余的角度旋转和角度扩展等问题，对于一般的乘除运算影响不大，对于脉动阵列来说，由于CORDIC计算存在误差通过脉动阵列逐级的积累而放大，甚至导致错误的输出结果。因此，传统的CORDIC不适合用于实现数字预失真的脉动阵列结构。因此，提出一种改进CORDIC算法来实现数字预失真，该方法易于FPGA实现、资源消耗少且计算速度和精度方面都有所提高。

1 CORDIC基本原理

坐标旋转数字计算机（Coordinate Rotation Digital Computer CORDIC），是由Jack Volder[6]于1959年提出的，广泛应用于基本函数的计算。为了扩展可解决的基本函数个数，之后又相继提出了统一的CORDIC算法和并行的CODIC算法，大大提高了CORDIC算法的迭代速度和精度。随着可编程逻辑器件（FPGA）规模的增大，使得利用硬件电路实现该算法成为可能。

下面来描述CORDIC算法的基本原理，如图1所示，假设平面直角坐标系一矢量（x0，y0），将其顺时针旋转角度θ，得到新的矢量坐标（x1，y1）如式（1）所示:

图1 CORDIC算法向量旋转原理图

进一步推导得:

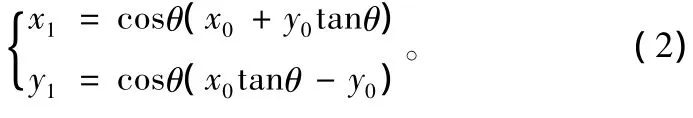
任意角度都可以表示成一系列的基本角度的线性之和，则旋转角度θ可表示为[5]:

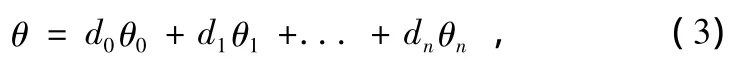
式中，di表示旋转的方向是顺时针还是逆时针di={+1，－1}。为了便于硬件实现，令θi=tan－1（2－i），这里引入一个方程:zi+1=zi+diθi，表示迭代过程旋转的角度之和。则式（2）可重写为:

向量经过一系列的基本旋转后可逐渐逼近目标向量，此时有:

式中，cosθi表示旋转校正因子，令Kn=cosθi为经过n步迭代后总的旋转校正因子，则有:

当n足够大时，Kn近似取值为一常数0.607 253，可以将这个常数作为系统的增益来处理。

2 CORDIC的改进

2.1 多余旋转角度问题

如旋转角度θ=arctan（20）时，理论上经过第一次旋转后已经得到了目标向量，而传统CORDIC需要经过N次旋转，这就导致旋转误差。在每一级旋转增加控制信号来判断是否进入下一级的旋转，避免一些不必要的旋转。

2.2 角度扩展问题

由于θi=tan－1（2－i），根据推导CORDIC算法的旋转角度范围为（－99.9°，+99.9°），不能覆盖整个坐标平面。为了确保算法的收敛，文献[5]中采用增加2个45°的迭代来达到收敛，这种方法对于单输入信号较为实用，然而对于预失真来说，由于预失真训练器采用了多项式模型，增加迭代次数的同时增加了算法的复杂度，为此对输入（x0，y0）进行了预处理，具体操作步骤如下:预先判断向量的象限，将其搬移到第一和第四象限。最后利用一个符号标志位sign判断旋转角度和输出。即当x＜0时，sign=1;当x＞0时，sign=0。这样将信号的旋转角度限制在了第一和第四象限，从而降低了额外的迭代带来的复杂度。

2.3 校正因子分解

由式（6）可知，直接在旋转之后增加一个乘法器来补偿旋转模长，这种方法使得原本由移位器加减实现的流水线结构变得复杂，乘法器的速度限制了整体的流水线吞吐量，同时还增加了硬件资源消耗。为了解决乘法运算所带来的资源消耗和运算速度的降低得问题，每一级旋转所对应得伸缩因子Ki的理论值和近似值，可通过简单地移位和加减来实现长度补偿如表1所示。

表1 第i次旋转对应的校正因子值

2.4 改进CORDIC流水线结构分析

以开根号运算为例，采用Verilog HDL语言描述改进CORDIC算法的向量模式，数据位宽为14bit，角度位宽为16bit，流水线级数为13级，Quartus II仿真分析和综合结果如图2所示。

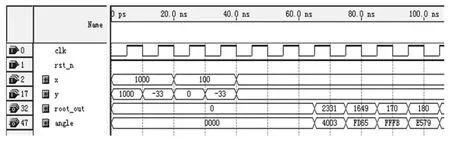
图2 改进CORDIC算法Quartus II仿真图

表2和表3分别列出了CORDIC算法改进前后的资源和精度对比。

表2 改进前后运算速率及资源对比

表3 改进前后计算精度对比

从表2和表3中可以看出，由于加入了控制信号和符号标志位，逻辑资源消耗有所增加，但改进后的CORDIC算法的运算速率和计算精度都有提高，且没有乘法器和ROM存储单元。同时对于特殊的角度值，运算结果与理论之间没有误差，极大地减少了迭代的次数。这对于预失真这种数据处理量大的应用，可以节约许多时间。

3 数字预失真实现

基于改进CORDIC算法的四通道QR-RLS脉动阵列实现结构如图3所示，图中三角阵列有2种运算单元，圆形表示边界单元，工作在向量模式;方形表示内部单元，工作在旋转模式[7－10]。阵列边界单元工作在向量旋转模式，此时φ－CPE单元将输入数据xin旋转到x轴，输出向量为，同时给出旋转角度φ，此时的2个θ－CPE单元仅有左边的工作，它输出将消去的旋转角度θ，同时储存相关矩阵R值。内部单元工作在旋转模式，如图4所示。根据边界单元的φ和θ实施旋转，并将旋转角度值传递给下一个单元。CPE单元设计采用高速流水线结构，采用这种结构能够获得较高的数据速率，在单元执行第i次旋转时，数据能够同时从顶部输入，采用N级相似的算法单元在同一个时钟周期内并行工作，平均完成一次计算只需一个时钟周期，这极大地节约了运算时间。

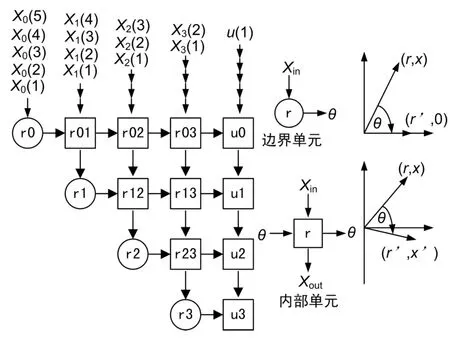
图3 四通道QR-RLS算法的脉动阵列结构

图4 基于改进CODRDIC算法的CPE单元

4 实验结果

将2种算法实现的脉动阵列在FPGA上实现，对比结果如表4所示。

表4 两算法实现脉动整列的对比

由表4可以看出，在资源消耗方面，脉动阵列采用了3阶5抽头的多项式，由于传统的CORDIC算法使用了ROM表和乘法器单元，总的资源消耗就相当的大。在运算速度上，传统的CORDIC算法使用了乘法器，限制了脉动阵列的整体速度，改进算法的IP CLK相对传统的提高了100MHz，因此参数提取的时间将近节约一半的时间。

预失真实验测试平台如图5所示，频谱分析仪观测功放输出频谱如图6所示。从图中可以看出，传统的CORDIC算法实现的参数提取算法预失真效果不明显，甚至有些地方失真更为严重，这是由于传统CORDIC本身存旋转误差以及多余的角度旋转造成的误差，这些误差经过脉动阵列逐级传递，误差积累导致最终的参数提取不正确。然而改进CORDIC算法有效地避免了多余迭代带来的误差，获得了较好的预失真效果。

图5 硬件测试平台

图6 2种算法实现DPD输出频谱比较图

5 结束语

对传统CORDIC算法的原理及其存在的问题进行了深入的分析，从多余角度旋转、旋转角度扩展和模校正因子分解3个方面对算法进行改进，采用跳跃旋转、象限搬移以及移位加减来实现CORDIC算法。与传统的CORDIC算法相比较，节省了大量的硬件资源，提高了运算速度和精度，易于FPGA实现。最后，采用改进的CORDIC算法实现了预失真参数提取算法，实验结果显示预失真效果改善了18dB左右，满足功率放大器的实时性和高线性度要求。

[1]LIU Tai-jun，SLIM B，FADHE M，et al.Augmented Hammerstein Predistorter for Linearization of Broad-Band Wireless Transmitters[J].IEEE transactions on Microwave Theory and Techniques，2006，54（6）:1340－1349.

[2]MORGAN D R，MA Z KIM J，ZIERDT M G，et al.A Generalized Memory Polynomial Model for Digital Predistortion of RF Power Amplifiers[J].IEEE Transactions on Signal Processing，2006，54（10）:3852－3860.

[3]CAVERS J.Amplifier Linearization Using A Digital Predistorter with Fast Adaptation and Low Memory Requirements[J].IEEE Trans.Veh.Technol，1990，39（4）:374－382.

[4]艾渤.高功率放大器线性化技术研究[J].微波学报，2007，23（1）:62－69.

[5]WU Cheng-shing，AN Y W.Modified Vector Rotational CORDIC（MVR-CORDIC）Algorithm and Architecture[J].IEEE Transactions On Circuits and Systems-II:Analog and Digital Processing，2001，48（6）:548－561.

[6]VOLDER J E.The CORDIC Trigonometric Computing Technique[J].IRE Trans.Electron.Computers，1959，（C－8）:330－334.

[7]HAYKIN S.Adaptive Filter Theory[M].2nd ed.Englewood Cliffs，NJ Prentice-Hall，1991:210－254.

[8]WARD C R，ROBSON A J，HARGRAVE P J.Application of A Systolic Array to Adaptive Beam Forming[J].IEEE Proceedings of Communications，Radar and Signal Processing，1984，131（6）:638－645.

[9]MA J，DEORETTERE E F，PARHI K K.Pipelined CORDIC based QRD-RLS Adaptive Filtering Using Matrix Look-Ahead[J]IEEE Workshop on Signal Processing Systems，1997，35（2）:131－140.

[10]CHANG L W，LEE S W.Systolic Arrays for the Discrete Hartley Transform [J].IEEE Trans.Signal Processing，1991（29）:2411–2418.