一道竞赛练习题的思维拓展

王 勇

(浙江省浦江中学,浙江 浦江 322202)

在竞赛培训中,对习题的思维拓展是非常重要的,笔者在训练学生思维拓展方面特别注重这方面的培养.对于同一个问题,如果从不同的角度,不同的知识去理解它,会有不同的认识和观点.

一题多解对拓展学生的思维边界,提升学生的思维能力对竞赛的学生尤为重要.在这里针对运动学的一道习题,给出了多种解法和大家交流.

例题.设湖岸MN为一直线,有一小船自岸边的A点沿与湖岸成15°角方向匀速向湖中驶去,有一人自A点同时出发,他先沿岸走一段再入水中游泳去追船.已知人在岸上走的速度为v1＝4m/s,在水中游泳的速度v2＝2m/s.试求船速至多为多少,此人才能追上船？

图1

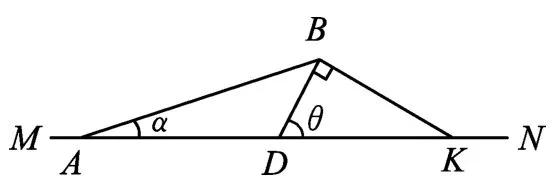
图2

解法1:(微元法)如图1所示,设人在B点刚好能追上船且以自D点处入水所用时间最短.则自D左、右侧附近C、E点入水刚好追到船所用的总时间相等.在BC段上取BF＝BE,则应有人走CE段和游CF段用时相等,即当C点无限靠近D点时,E必同时靠近D,由图近似有故求得θ＝60°.由于此时C点是无限靠近D点,故BC与BD接近重合,即∠BDN＝θ＝60°.由上得出,当人自D点入水沿与岸成θ＝60°方向游泳刚好追到船,对应船速最大设其为v,如图2所示.过相遇点B作BK⊥BD交MN于K,因θ＝60°所以DK＝2DB,又v1＝2v2则人游DB段与走DK段所用时间相等.故人自出发到在B点追上船的时间等于他由A点走到K点的时间,即在△ABK中由正弦定理有

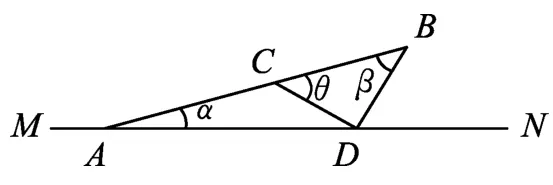
图3

解法2:(极值法)如图3所示,设人沿岸走到D点时,船已航行至C点,此时人入水游泳追船且刚好在B点追上船.在△ACD中由正弦定理有又设船速为v,人由A点走到D点所用时间t,则

代入上式有

在△CDB中,由正弦定理有

设人游过DB段的时间为t′,则BD＝v2t′,CB＝vt′.同样代入上式得

联立(1)、(2)式且v1＝2v2,则

又由△ACD可见,要v尽可能大,即需尽可能大,而θ越大则AC越大,需θ尽可能大.又由于α为一常数,易判断θ－α＝∠ADC为锐角.故sin(θ－α)最大时θ最大.由(3)式可见,当sin(θ＋β)＝1时,sin(θ－α)有最大值,此时对应为θ＝45°,由此β＝45°,则△CDB为等腰直角三角形.由(2)式可得

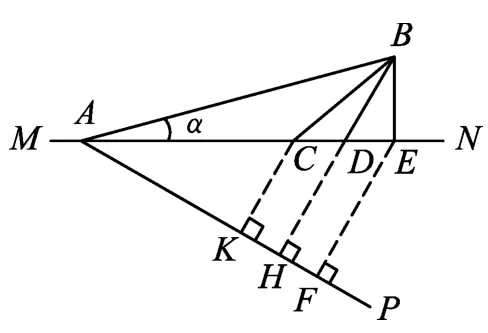
图4

解法3:(等效法)如图4所示,设人在B点刚好追上船,则人可能走多条路径如A→C→B、A→D→B…等.在这些路径中费时最少对应着允许的最大船速.如图在湖岸这边作∠NAP＝30°,自C、D、E各点分别向AP引垂线CK、DH(设B、D、H刚好在一直线上)和EF.设想图中MN的下侧也变成了湖水区域,则人由K点游泳至C点的时间与人在岸上由A走至C点的时间是相等的(因v1＝2v2,而AC＝2KC),故人按题给情况经A→C→B所用的时间和假想人全部在水中游过路径K→C→B相等.同理,与上述的另两条实际路径等时的假想路径是H→D→B和F→E→B.由于在这些假想路径中速度大小都一样,故通过路径最短费时少,显然是通过直线HDB费时最少.

由以上分析可知,人沿等效路径HDB刚好在B点追上船时,对应允许船速的最大值.设其速度为v则有由于△AHB为等腰直角三角形,则,故

解法4:(图像法)如图5所示,设人自开始运动历时t.若人自一开始就跳入水中游泳,则他可以达到以A为圆心、以v2t为半径的半圆形水面上的任何一点.若他一直在岸上走,则可走到AF＝v1t的F点.若他先在岸上走一段再入水中游,如在C、D、E各点入水,则可分别达到以C、D、E为圆心的较小的半圆形水面范围内的任何一点.可见,只要选择恰当的入水点和入水后恰当的游向,人在时间t内可达到图5中PQF水面区域内的任何一点,而此区域外的任何一点,都不可达到.可见在时刻t时,若船还在此区域内,则人总可以追到船,否则人将追不到船.临界情况是船刚好在时刻t时到达此区域的边界线上,如图中的B处,此情况对应允许的船速最大值.在直角ΔAKF中,由于AF＝2AK,所以∠AFK＝30°.

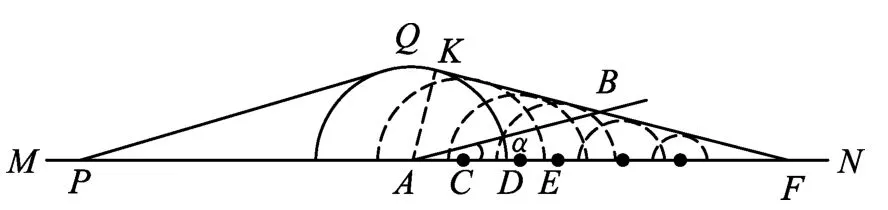
图5

而∠ABF＝180°－(∠AFK＋α)＝135°.

在△ABF中有

又有

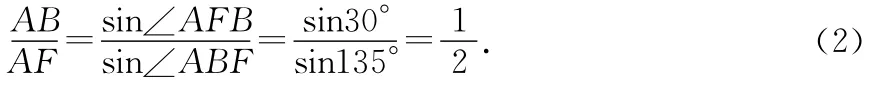
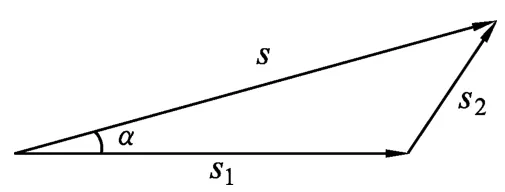
图6

解法5:(演绎法),设船出发后历时t被人追上,则船在t内的位移为s＝vt,又设人在岸上走的时间为kt(0＜k＜1),位移为s1＝kv1t,则人在水中游泳时间为(1－k)t,对应的位移为s2＝(1－k)tv2.上述3段位移构成如图6所示的封闭三角形.由余弦定理有

将s、s1、s2的函数式及v1、v2、α的值代入并整理有

将上式看作是关于k的二次方程,结合本题的实际可知它必有实数解,故应有Δ≥0即解此不等式得由本题的条件可知,只能取即若要人能追上船,最大船速

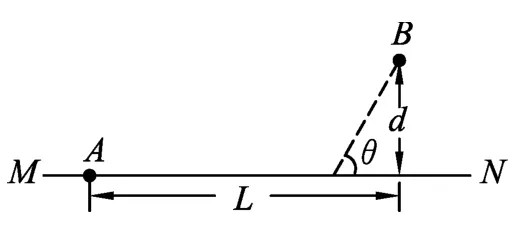
图7

解法6:(演绎法)如图7所示,设人自岸上某处沿与岸成θ角的方向游去,恰与船相遇于B点,设B点与岸相距为d,BA在岸上的投影长为L,则人由A至B所历的总时间为

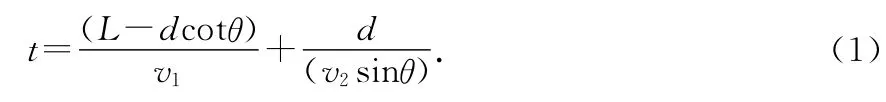
上式说明t与θ有关,且在d、L、v1、v2一定时由θ决定.现研究函数

有

将(3)式展开并整理有

将上式看成是关于cosθ的二次方程,则对应每一个实际可能的过程,都应有实数解,故

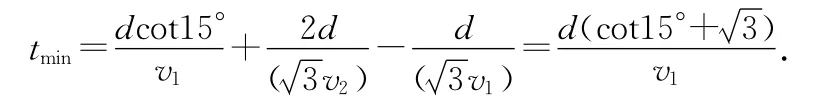
图8

解法7:(矢量法)设人先在岸上走一段时间,在入水游泳追船.以船为参照物,由于人和船是同时由A出发,则人在岸上走时,船看到人正在由船所在位置逐渐“离去”,离去的相对速度为u1.人在水中游时,船则看人正逐渐“返回”,其返回的相对速度为u2.要人“返回”到船上,则u1与u2必方向相反.

由速度合成的矢量三角形法则可知,u2矢量末端必终止在图8所示的u1的反向延长线上.为使v尽可能大,即要尽可能大(因v2的大小是恒定的),故图中v2应尽可能短,这对应于v2与图中虚线垂直的情况.同时由于v1＝2v2,可见图中v2与v1的夹角为60°,则由－v、v2、u23个矢量组成一等腰直角三角形,故有

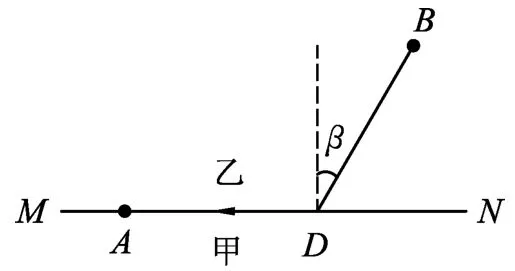
图9

解法8:(比较法)如图9所示设想MN为光的甲、乙两介质的分界面,光在甲介质中的速度为v1,在乙介质中的速度为v2,则当乙介质中的B点发出的光以临界角入射到分界面上时,将产生有折射光在甲介质中沿界面由D至A的“掠射”现象.由费马原理,可知B→D→A是光线由B传至A费时最少的路径.将此结论类比于本题中人由A点至B点的情况,即人应取A→D→B的途径费时最少.(下同解法1,略)