立足例题拓展提升学习能力
刘傲艳
同学们在本章的学习中,运用概率知识去分析问题和解决问题时,一定会感到困难,这就需要同学们学会将例题进行变式和拓展,来提升自己解决问题的能力,这里给出几个例子供同学们参考.
例1 在一个不透明的口袋中,装着10个大小和外形完全相同的小球,其中有5个红球,3个蓝球,2个白球,把它们搅匀以后,请问:下列哪些事件是必然事件?哪些是不可能事件?哪些是随机事件?
(1) 从口袋中任意取出一个球,它刚好是白球. ( )
(2) 从口袋中一次取出3个球,它们恰好全是蓝球. ( )
(3) 从口袋中一次取出9个球,恰好红、蓝、白三种颜色全齐. ( )
(4) 从口袋中一次取出6个球,它们恰好是1个红球,2个蓝球,3个白球. ( )
【解答】(1) 随机事件;(2) 随机事件;(3) 必然事件;(4) 不可能事件,因为白球一共只有2个.
变式拓展1:现有5个红球,3个蓝球,2个白球,这10个球除颜色外,其余特征完全相同,请你在盒子里放入若干个球,设计一个游戏方案,使得从盒子里一次摸出三个球,可能是两个红球,一个白球.
【解答】从盒子里一次摸出三个球,可能是两个红球,一个白球这个事件是随机事件,因此在设计游戏方案时,只要保证盒子里至少有4个球,其中必须有两个红球,一个白球.
变式拓展2:现在有5个红球,3个蓝球,2个白球,这10个球除颜色不同外,其余完全相同,请你在盒子里放入若干个球,设计一个必然事件.
【解答】答案不唯一,比如:盒子里只放红球,任意摸一个球,摸到的球是红球;比如盒子里放10个球,一次性取出9个球,红、蓝、白三个颜色全齐等.
【说明】本例及变式拓展主要是对随机事件、必然事件和不可能事件进行理解. 随机事件即在一定条件下,我们事先无法确定它会不会发生的事情;必然事件即在一定条件下,事先能肯定它一定会发生的事情;不可能事件即在一定条件下,事先能肯定它一定不会发生的事情. 理解这三个概念应从两个方面入手,即要注意:①在一定条件下;②事先能不能确定事件发生. 本例主要是已知在一定的条件下,并且给出某个事件,判断其是什么事件;变式拓展1则是条件未知,要求同学们根据事件来设计条件;变式拓展2则更为开放,条件和事件都未知,要求同学们既要设计条件又要设计问题. 这样设计的目的旨在引导同学们深入理解剖析必然事件、不可能事件和随机事件的概念,并知道这三种事件是在一定的条件下才成立的,一旦条件发生变化,这三种事件也有可能互相转化,培养思维的灵活性和深刻性.
例2 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,某同学说,摸出的球不是白球就是红球,所以摸出白球和摸出红球这两个事件可能性大小相等,你认为他的说法正确吗?如果不正确,哪一种可能性大?为什么?
【解答】一只不透明的盒子装有2个红球和1个白球,由于这3个球除颜色外都相同,所以搅匀后从中任意摸出1个球,摸到每一个球的可能性是相同的. 红球有2个,把它们编号为红球1、红球2;那么,搅匀后从中任意摸出1个球有3种可能的结果:红球1、红球2、白球,因此任意摸出1个球,摸到红球的可能性大.
【说明】本例首先要理解每次摸到的球的颜色是不确定的,摸到每一个球的可能性是相同的,因为红球的数量与白球的数量不等,可以把两个红球编上号码为红球1、红球2,因而摸到红球与摸到白球机会不均等,即摸到红球的可能性大于摸到白球的可能性. 通过本例同学们要理解:①事件发生的可能性大小是由发生事件的条件来决定的;②可能性的大小与数量的多少有关:数量多则可能性大,数量少则可能性小.
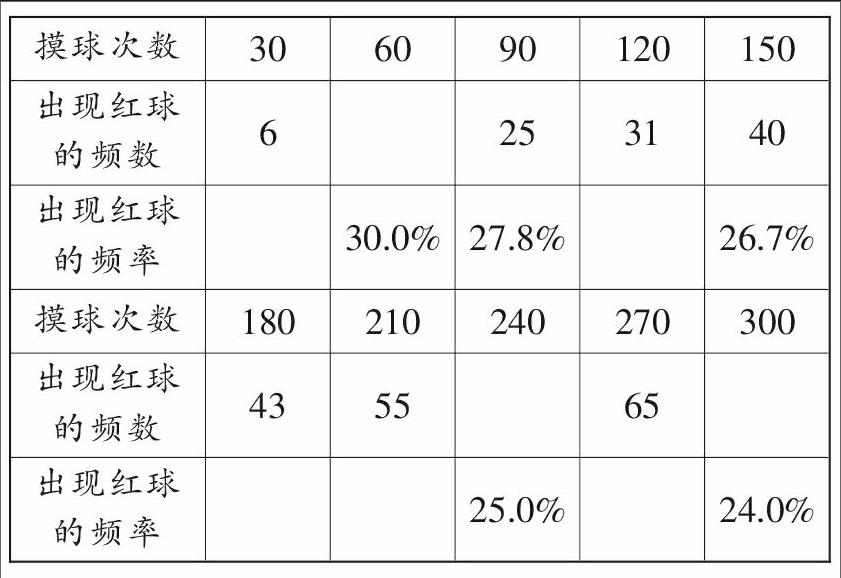
例3 在一个不透明的袋中有大小相同的4个小球,其中2个为白球,1个为红球,1个为蓝球,每次从袋中摸出一球,然后放回搅匀再摸,小刚在摸球实验中得到下列表中部分数据.
(1) 请将数据表补充完整;
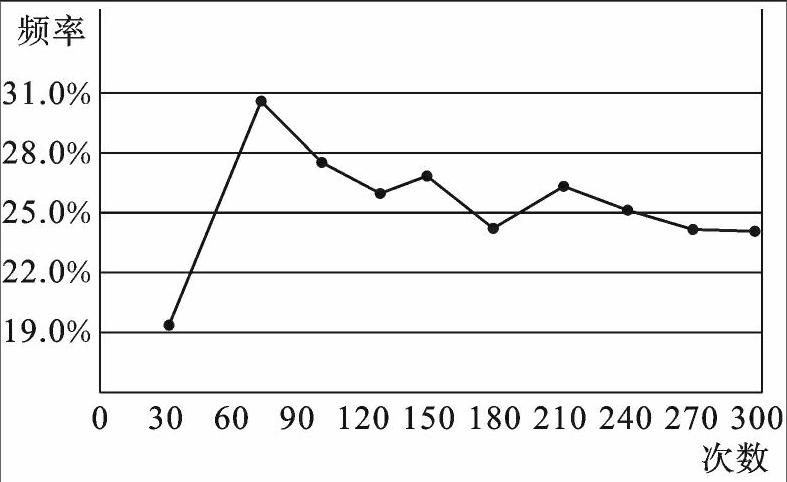
(2) 画出折线图;
(3) 观察上面的图表可以发现:随着实验次数的增大,出现红色小球的频率______.
(4) 如果按此题中的方法再摸球300次,并将这300次实验获得的数据也绘成折线图,那么这两幅图会一模一样吗?为什么?
(5) 请估计,当实验次数很大时,出现红色小球的频率将会接近多少?
(6) 假如你去从袋中摸出一球,你摸得红球的成功率约是多少?
【解答】(1) 上排(频数)答案分别为:18,60,72,下列(频率)答案分别为:20%,25.8%,23.9%,26.2%,24.1%.
(2) 折线图如图所示.
(3) 逐渐稳定.
(4) 不太可能一模一样,因为出现红色小球的频率是随机的.
(5) 约25%.
(6) 约25%.
【说明】本例复习了频率的定义、折线图画法;运用了在实验中寻找规律的方法,只有正确理解“每次摸出的结果是随机的、无法预测的,但随着实验次数的增加,隐含的规律逐渐显现,事件出现的频率逐渐稳定到某一数值”才能准确理解此题. 对于类似的题目要注意两点:第一,对象出现的次数与总次数的比值(或者百分比)叫频率;第二,在一定条件下,大量重复进行同一实验时,随机事件发生的频率会在某一个常数附近摆动. 在实际生活中,人们常把实验次数很大时,事件发生的频率作为其概率的估计值.
(作者单位:江苏省常州市清潭中学)

