滑坡监测中监测精度及复测周期的合理确定

李 雷

(中铁第四勘察设计院集团有限公司，湖北武汉 430063)

通常情况下，滑坡监测的具体目有以下两个方面:(1)了解滑坡发生以及演变的过程，为边坡稳定性分析和预测、预报提供准确可靠的数据;(2)检测防治工程的效果。综合说来，其根本监测对象是坡体的位移变化。近年来，已有人对滑坡监测精度以及监测周期的确定方法进行研究，认为监测精度以及周期的确定应从以下三个方面进行考虑:①监测体的实际情况;②现有监测规范的要求;③国内外滑坡监测的经验。

以上提出的方法没有充分考虑滑坡监测精度、复测周期和斜坡位移之间的关系以及斜坡变形的特点，在参照滑坡变形监测规范的时候存在很大的盲目性，如果确定的监测精度过低，或者复测的周期不合理，位移的变化往往被测量的误差所掩盖，监测结果不能反映斜坡变形的真实情况。因此，有必要研究滑坡监测精度、复测周期和斜坡位移之间的关系，在此基础之上，结合斜坡变形的特点，提出合理确定滑坡监测精度和复测周期的方法。

1 监测精度、复测周期与斜坡位移之间的关系

设t时刻斜坡体上监测点P的三维坐标为xt、yt、zt，经过时间 Δtx、Δty、Δtz(Δtx、Δty、Δtz分别为三个方向的观测周期，测得其三维坐标分别为 xt+Δt、yt+Δt、zt+Δt，则P点两期监测的位移量为

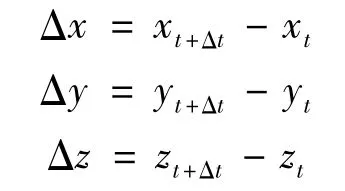
水平和垂直位移速度分别为

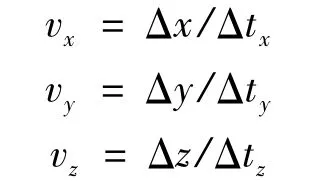
根据概率统计基本原理，假定k为由误差分布类型和置信水平所决定的系数，Δx、Δy、Δz的中误差分别为 σΔx、σΔy、σΔz，则只有当下列三式

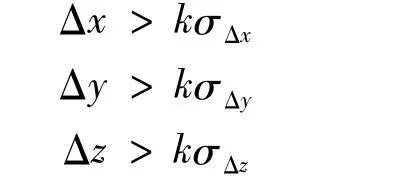
中至少有一个成立时，才可以认为监测点在两次监测期间产生了位移变化;如果上述三式均不成立，则可以认为监测点坐标的变化是由于观测误差引起，不能精确地反映监测点的位移变化。

假如监测点在复测周期内未产生位移，则两期监测的坐标差Δx、Δy、Δz可视为均值为零而方差分别为的正态随机分布，故系数k可由下式确定

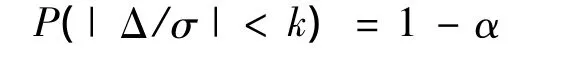
式中 Δ——相邻两期监测的坐标差(Δx或 Δy或Δz);

σ——坐标差的中误差(σΔx或 σΔy或 σΔz);

α——显著水平。

根据以上的分析以及公式，解算可以得到如下公式

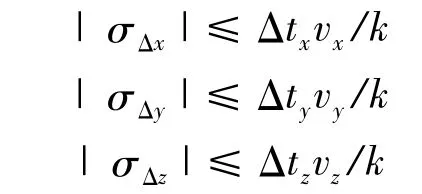
由以上三式又可以求得

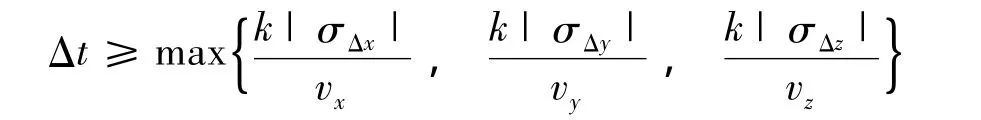
上述公式揭示了监测精度、监测周期和坡体位移三者之间的关系，为合理确定滑坡变形监测的精度以及复测周期提供了理论依据。为了定量地观察和分析滑坡位移速度、观测精度以及观测周期三者之间的关系，现选取三者中的几组数值，见表1。

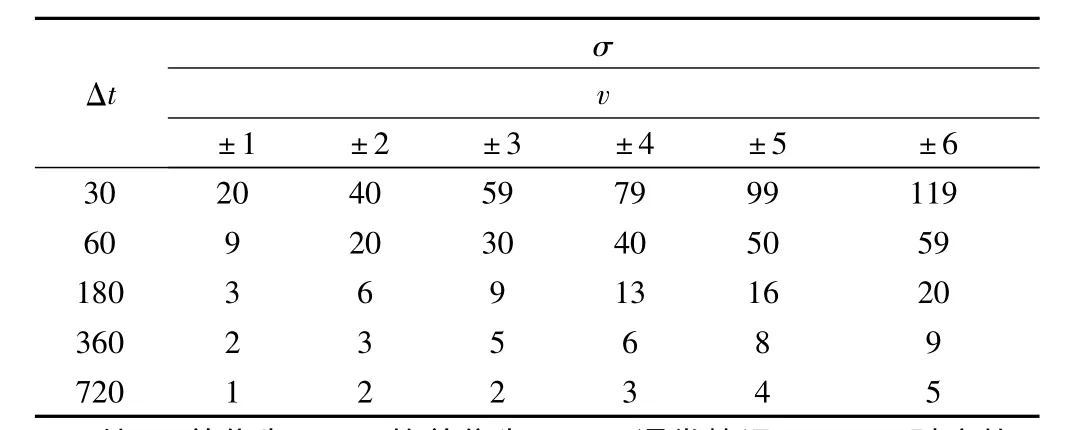
表1 监测精度监测周期和位移之间关系

2 合理确定监测精度以及精测周期的方法

2.1 确定合理的观测精度

分析上表中的数据，不难得出如下结论:

①当位移速度很小时，要求有很高的监测精度;

②当位移速度较大时，可以相应的降低监测精度;

③当位移速度一定时，监测周期越短，监测的精度越高;

④随着位移速度的增大，必须缩短相应的监测周期，同时适当降低观测精度。

2.2 确定合理的观测周期

如上面所述，滑坡的位移速度与滑坡变形监测的精度以及复测周期之间存在一定的关系，如果已知位移速度和观测周期，可以确定必要的监测精度;如果已知位移速度和监测精度，可以确定合理的监测周期。目前滑坡变形监测主要采用常规大地测量与GPS方法相结合，其位移的大小主要由监测点的三维坐标决定，复测周期可由下述方法初步确定:

①当vx≥max{vy，vz}时，说明 x的方向为位移的主要方向，则取Δt=Δtx;

②当vy≥max{vx，vz}时，说明y的方向为位移的主要方向，则取Δt=Δty;

③当vz≥max{vx，vy}时，说明z的方向为位移的主要方向，则取Δt=Δtz;

④当 vx≈vy≈vz时，取 Δt=min{Δtx，Δty，Δtz}。

如果水平位移与垂直位移不是同时监测，垂直方向上的监测精度以及周期也可以通过前面位移与两者之间的关系来确定，具体方法是要确定出竖直方向上位移的速度，此时平面上的监测周期可以按如下方法来确定:

①当 vx≥vy时，Δt=Δtx;

②当 vx≤vy时，Δt=Δty;

③当 vx≈vy时，Δt=min{Δtx，Δty}。

以下通过具体实例加以说明。某单位曾在1996年～1998年连续两年对四川某市某峡口进行变形监测，主要监测方法采用的是GPS静态监测，监测期间滑坡体正处于变形加剧阶段，监测周期由专家组确定为每月一次，该坡体的位移主方向为平面内的y坐标方向，由实际监测得到的数据求得的部分监测点月平均位移速度如表2。

表2 四川某市某峡口部分GPS监测点点位以及位移平均速度

由于观测周期已经确定，位移速度也已经计算得出，我们可以根据上文的内容确定出各监测点必要的观测精度，如表3。

表3 四川某市某峡口部分GPS监测点必要监测精度

从表3可以看出，各监测点的必要监测精度不同，其中最高的必要精测精度和最低的必要监测精度相差约在100倍左右。由此可见，滑坡体上位置不同监测点，其位移速度往往不一样，因此不同的监测点对监测精度的要求也会不一样。

据资料显示，通过双频GPS接收机进行静态监测，若要求监测精度达到±2.4 mm，观测1 h即可;如果要求监测精度达到1.0 mm，则至少连续进行6 h的观测，由此可见，随着监测精度的降低，可以大大缩短监测的时间。以上的实例如果按照精度1.0 m进行变形监测，则只有50号点才有必要，而对于其他点来说这样的精测精度过高，会造成人力、物力以及时间的大量浪费，因此这个监测精度的确定就是不合理的。可以采用如下的方法解决这个问题:在每期监测结束之后，可以根据当期的监测周期以及计算得出的监测点位移速度分别求得各监测点的必要监测精度，在接下来一期的监测过程中，根据求得的各点的监测精度，不同的点采用不同的监测精度，监测精度相差不大的点同时进行监测，既可以满足滑坡变形监测的要求，又可以节省大量的时间以及人力和物力，取得预期的效果。

3 结束语

在斜坡变形过程的缓慢变形和变形发展阶段，由于坡体位移的速度不是很大，需要有较高的监测精度，可以适当采取较长的复测周期。在这个阶段应该根据监测所采用的仪器和方法，分析和确定出在各方面条件可行的情况下所能达到的最高监测精度，按照此监测精度进行监测，可以通过这个监测精度以及求得的坡体位移速度确定合理的监测周期。

在滑坡体变形加剧和急剧变形两个阶段，坡体位移速度大，此时监测工作的关键问题是怎样根据位移量的大小和必要监测精度确定最恰当的监测周期，从而及时地捕捉到滑坡体的变形信息，为滑坡体的变形提供及时准确的预报。因此，在这两个阶段应该首先确定出监测周期，再根据求得的坡体位移速度算出合理的必要监测精度。

［1］ 晏同珍，杨顺安，方云．滑坡学［M］．武汉:中国地质大学出版社，2000

［2］ 陶本藻．自由网平差与变形分析［M］．武汉:武汉测绘科技大学出版社，2000

［3］ 黄声享．监测网的稳定性分析［J］．测绘信息与工程，2001(3)

［4］ 盛骤，谢式千，潘乘毅．概率论与数理统计［M］．北京:高等教育出版社，1999

［5］ 陶本藻．测量数据统计分析［M］．北京:测绘出版社，1993

［6］ 杨叔子，吴雅，等．时间序列分析的工程应用［M］．武汉:华中理工大学出版社，1991

［7］ 陈永奇，吴子安，吴中如．变形监测分析和预报［M］．北京:测绘出版社，1992

［8］ 施闯．大规模、高精度GPS网平差处理与分析理论及其应用［D］．武汉:武汉测绘科技大学，1999

［9］ 乔建平，陈永波．用GPS观测滑坡变形的结果分析［J］．水土保持学报，2000，14(1)

［10］胡小军，赵子俊．砂坝滑坡变形监测与分析［J］．铁道勘察，2007，24(2):55-58

［11］阎继峰．曹家坡滑坡工程地质特征研究［J］．铁道勘察，2009，24(3):46-48