金属颗粒的光散射模拟

邓志宏，彭柯铭，夏湘芳，刘 归，王国友，陈光伟

（湖南工业大学 理学院，湖南 株洲 412007）

金属颗粒的光散射模拟

邓志宏，彭柯铭，夏湘芳，刘 归，王国友，陈光伟

（湖南工业大学 理学院，湖南 株洲 412007）

以Mie理论为基础，用数值计算方法分析了金属球型颗粒的光散射特性，给出了金属颗粒对平行入射光的散射强度函数和散射偏振度的数值计算方法。利用Matlab软件模拟得到了散射光强度函数和偏振度随散射角和尺度参量变化的三维图。模拟结果表明：偏振峰个数随尺度参量的增大而增多，偏振峰之间的距离随尺度参量的增大而缩小。这种变化趋势可以作为检测金属颗粒粒径的理论依据。

Mie理论；散射光强度函数；偏振度

随着科学技术的发展，研究和制备的颗粒尺度已达到了纳米级，各科研领域都出现了与纳米和微米级颗粒相关的技术问题[1-2]。如对煤电企业排放烟尘的检测，生命科学领域中细胞大小、浓度的测量，溶液中悬浮颗粒、城市中空气污染物PM2.5的测量等[3-4]。描叙微小颗粒光散射的Mie理论是检测微小颗粒尺度和浓度的理论依据，其应用领域非常广泛，如利用该理论研制的尘埃粒子计数器，可以测量城市中尘埃粒子的粒度和密度。在采用不同方法制造的各种粒度测量仪器中，唯有根据光散射法制造的设备因具有实时无损等优点而成为主要的测量设备。因此，完善和应用Mie理论具有重要的理论意义和现实意义。本文根据Mie理论，利用数值模拟软件Matlab仿真得到散射相关物理量随2个参量（散射角和尺度）变化的图像，并对某些尺度参量下散射光的偏振度随散射角变化的规律进行分析。

1 Mie散射理论

Mie 散射理论的数学推导过程较繁琐，如何实现 Mie 散射有关物理量的精准、快捷运算，来满足实际应用的需要，是人们多年来研究的课题。在实际运用过程中，必须先得到各种微粒在不同折射率下散射场分布的理论数据及图像，然后与微粒对光的散射场的实际测量数据对比分析，进而得出相应结论。以下是Mie 散射理论的数学表达[5-6]：

S1和S2是散射振幅函数；

Ii是入射光强度；

r是颗粒到观测点的距离；

P是散射光的偏振度；

m是球与介质之间的相对复折射率；

an(x, m)和bn(x, m)是Mie系数；

τn和πn是散射相关函数，πn的运算初始数值为πn=0，π1=1；

p1是一阶Legendre函数；

2 数值模拟

在利用Matlab编程实现理论数值化时，运用三维矩阵变量可缩短数值运算时间。运算时间还与选取的散射角和尺度参量的取值间隔有关，取值间隔越大运算时间越短，但作出的图形精度降低。本文中散射角度取值间隔为每步0.5°，尺度参量取值间隔为0.2。选取复折射率m=3-2.5i的金属颗粒作为模拟对象[7]，其中复折射率的虚数部分表示金属颗粒的吸收系数。

垂直散射光的强度分布如图1所示。从图中可以看出，随散射颗粒尺度参量增大，散射光强分布更集中在小散射角上。

图1 垂直散射强度Fig.1 The vertical scattering intensity

平行散射光的强度分布如图2所示。从图中可以看出，平行散射光强的整体分布是，随散射角的增大先减小后缓慢增大。

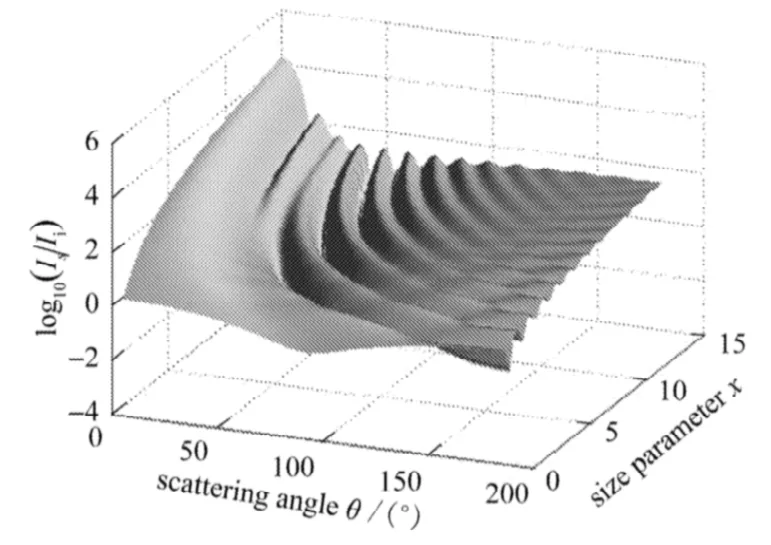
图2 平行散射强度Fig.2 The parallel scattering intensity

从图1和图2可以看出，垂直散射强度和平行散射强度的相同变化趋势是，随着尺度参量的增大波浪起伏增多。这是因为尺度参量是颗粒直径与散射波波长的比值，尺度参量越大在某个角度出现同向光强相消的可能性越大。

图3是散射光的偏振度变化情况。从图中可以看出，偏振度与光强分布一样有起伏，但偏振度图形的起伏更剧烈；光强主要分布在前向散射角，而偏振度的最高峰值并不出现在前向散射角。

图4和图5是对图3中偏振度三维立体图的切片图，图4中的散射颗粒尺度参量分别为1, 3, 6；图5中的散射颗粒尺度参量分别为9, 12, 15。

图3 偏振度三维立体图Fig. 3 3D plot of polarization

图4 x=1,3,6时的偏振度Fig. 4 Polarization at x=1,3,6

图5 x=9,12,15时的偏振度Fig. 5 Polarization at x=9,12,15

从图4可以看出，尺度参量为1时，只出现1个散射光偏振峰；尺度参量为3时有3个偏振峰；尺度参量为6时有5个偏振峰。

从图4可以看出，当尺度参量增大时，偏振度波峰个数增多；最强偏振峰都出现在50 到100 之间，但并没有趋势性规律。

从图4和图5还可以看出，偏振峰个数随尺度参量的增大而增多；偏振峰之间的角度差随尺度参量的增大而缩小。

3 结语

本文依据经典Mie散射理论，采用Matlab中的三维数组变量，快速得出了能显示金属粒子光散射特性的立体图。模拟结果显示，偏振峰个数随尺度参量的变大，从1个开始增加到十多个；偏振峰与峰之间的间隔随尺度参量的增大而缩小。现有的多数激光粒度仪都是根据颗粒被平行激光照射产生散射形成的光强分布来测试粒度分布的。本文所得结论可作为检测金属颗粒粒径的理论依据。

[1] 尹晋津，许利剑，曾晓希，等. 生物检测用纳米金粒子还原制备方法比较[J]. 湖南工业大学学报，2008，22 (1)：104-108. Yin Jinjin，Xu Lijian，Zeng Xiaoxi，et al. Comparison on Reductive Preparations of Gold Nanoparticles in Biodetection[J]. Journal of Hunan University of Technology，2008，22(1)：104-108.

[2] 肖 利，王春雄，刘建华，等. 纳米 CoFe2O4的制备中前驱体热分解过程研究[J]. 湖南工业大学学报， 2010，24 (4)：1-4. Xiao Li，Wang Chunxiong，Liu Jianhua，et al. Study on Thermo-Decomposition Process of the Precursor in the Preparation of Nano CoFe2O4[J]. Journal of Hunan University of Technology，2010，24(4)：1-4.

[3] 范淑红，刘亦武，谢 伟. 制备纳米SiO2的配方优化[J].湖南工业大学学报，2010，24(4)：56-60. Fan Shuhong, Liu Yiwu，Xie Wei. Optimization of Nanosilica Formula[J]. Journal of Hunan University of Technology，2010，24(4)：56-60.

[4] 赵友全，邹瑞杰，陈玉榜，等. 近红外散射法测定水中矿物油含量研究[J]. 光谱学与光谱分析，2012，32(5)：1213-1216. Zhao Youquan，Zou Ruijie，Chen Yubang，et al. Research on Detection of Oil in Water Based on Near-Infrared Scattering Method[J]. Spectroscopy and Spectral Analysis，2012，32(5)：1213-1216.

[5] van de Hulst H C. Light Scattering by Small Particles[M]. New York：Dover，1981：456-458.

[6] Bohren C F，Huffman D R. Absorption and Scattering of Light by Small Particles[M]. New York：Wiley，1998：781-790.

[7] 王少清，任中京，张希明，等. Mie散射系数计算方法的研究[J]. 应用光学，1997，18(2)：4-9. Wang Shaoqing，Ren Zhongjing，Zhang Ximing，et al. Study of Calculating Method of Mie Scattering Coefficient [J]. Journal of Applied Optics，1997，18(2)：4-9.

（责任编辑：邓光辉）

Metal Particle Light Scattering Simulation

Deng Zhihong，Peng Keming，Xia Xiangfang，Liu Gui，Wang Guoyou，Chen Guangwei
（School of Science，Hunan University of Technology，Zhuzhou Hunan 412007, China）

The light scattering characteristics of spherical metal particles are analyzed by numerical calculation method based on the Mie theory. A numerical calculation method for intensity function and polarization of the parallel incident beam scattered by small spherical particles is presented. The 3D graph for the intensity function and polarization varying with the scattering angle and the scale parameter was obtained by Matlab software simulation. The results show that with the increasing of scale parameter the number of polarization peak increases and the distance between the polarization peaks decreases. The variation can be used as theoretical basis for the detection of metal particle size.

Mie theory；scattering light intensity function；polarization

O439

A

1673-9833(2014)02-0106-03

2013-09-01

湖南工业大学自然科学研究基金资助项目（2013HZX24）

邓志宏（1980-），男，湖南益阳人，湖南工业大学讲师，硕士，主要从事实验教学以及理论物理和固体光谱学的研究， E-mail：zhihongdeng@126.com

10.3969/j.issn.1673-9833.2014.02.022