代数应用问题的文字表述对解题影响的研究

章 巍

（北京十一学校，北京 100039）

1 引 言

代数应用型问题（Algebra applied problems），也被称为代数文字题（Algebra Word problems），通常是指以现实世界中的事件与关系为题材、借助自然语言叙述来表达题意和题目中的数量关系、最终通过代数运算解决的数学问题[1~3]．

众所周知，代数应用题是中学数学教学的重点，也是难点．多数学者的共识是，解决代数应用题的能力不完全取决于解答纯粹数学题的能力，影响代数应用题解题的因素较多，其中很重要的一个因素是这类问题的“文字表述”．

一个典型的例子是 Hudson（1983）报告中被广泛引用的问题[4]：

问题1 有5只鸟和3只虫，则鸟比虫子多多少？

问题2 有5只鸟和3只虫，有多少鸟吃不到虫？

对于一年级学生，前一问题只有39%的学生可以解答，但后一问题却有79%的学生可以解答．Kintsch认为正是由于文字表述的细微变化，使后一个问题的解题者可以形成确定的情境模型——鸟吃虫．

另一个例子来自Cummins（1991）的研究[5]：

问题1 玛莉和约翰一共有5个弹子，其中玛莉有3个，约翰有多少个?

问题2 有5个弹子，3个属于玛莉，剩下的属于约翰，约翰有多少个?

一年级学生解答这两个问题的正确率分别是 30%和85%，相对于后面的问题，前面问题的解题者不得不进行推理，以确定集合间的关系，这增加了信息加工负荷和出现错误的几率[2]．类似的结果都说明，语言表述方面的某些改变确实能够有效地改善学生的解题状况[6]．

代数应用题中的语言具有自己特有的表达方式和习惯，与日常用语有差别．这种语言是慎重的、有意的、经过精心设计的，具有更高的抽象性，且语意转换频繁[7]．对这种语言的阅读与语文中的阅读和一般文学性的阅读不同[8]，理解数学应用题常常比理解相近事实的语文句子要有更高的能力．虽然数量关系结构是应用题的核心，但许多应用题的难易并不在于存在的数量关系，而在于对情节的陈述方式[9]．

需要指出的是，汉语自身的特点可能会进一步加剧这种理解的难度．与拼读语言相比，汉语语法对语句构成的要求相对宽泛，没有严格的“时态”、“格”、“语序”等限定，所以直感性低，阅读者往往很难利用语法结构来理解问题[9]．

但想要了解文字表述对解答代数应用题的具体影响，还需要将代数应用题语言的表述特征进一步分解为若干个关键指标，并逐一研究这些语言指标对学生解题的影响程度．

那么，代数应用题文字表述中的关键指标有哪些呢？

Mayer[10]认为，由于应用题含有较多的文字表述，因此学生在从文字中解读出数量关系时，容易发生语言知识的错误．刘四新[11]指出，遇到文字量较大的应用题时，学生很容易视觉疲惫，分不清主次，抓不住关键．从而说明，文字数量是影响学生解决应用问题的关键指标之一．

在 van Dijk和 Kintsch提出的话语理解（Discourse comprehension）理论框架中，如果问题所包含的情境或动作是学生所熟悉的，他们将比较容易形成问题模型[2]．施铁如[12]研究了认知模式对解代数应用题的影响，指出对应用题类型的把握在很大程度上决定着学生能否迅速、准确地解答问题．Hinsley[1]等的研究表明，儿童最初往往只能根据应用题故事内容的相似性，而非解题程序的相似性对问题进行分类．由此可见，不同的问题背景是影响学生解题难度的另一个重要指标．

陈英和[13]等人发现学生在解应用题时，首先要用自己独特的方式重新组织问题中的条件．而多数情况下，各国自然语言的句法结构与代数表达式的结构都会有差异，因此Kieran提出，解应用题时产生错误的一个重要原因是多数学生习惯按照语言顺序去逐句将文字翻译成代数表达式，这就使语言结构与代数结构之间的冲突在所难免[10]．李陆平[7]指出，当题目中的叙述形式与生活行为顺序不一致时，学生思维不易逆转．所以，语言的表述顺序也是影响学生解题的一个指标．

Yoshida[14]等人的研究结果表明，学生对题目中的隐含条件的识别与使用对解题正确率有显著影响．周新林[2]认为，应用问题往往在语言陈述上非常标准简练，有一些潜在的关系不直接陈述出来，学生解答时往往比较困难．因此，含有隐蔽或多余已知数的应用题是考查学生对应用题认知的一项指标．

同时，前期问卷的结果也显示，学生对应用题感到的困难在上述几方面也表现得相对突出．

综上所述，可以析出的代数应用题文字表述中的关键指标有：

语量——即题目中文字的客观数量；

语境——即题目所表述的整体情景；

语序——即题目中文字表述的顺序与解题时使用的数量顺序的一致程度；

关键词的隐蔽程度——即解题所用到的关键条件的显现度．

2 研 究

2.1 被 试

被试来自两所普通初中八年级的学生，按照最近期末统一调研考试的成绩，分别选取120~115分、95~90分和75~70分的学生各100名，分别记为高分组、中分组和低分组，共计 300人．再将这 3个不同分数段组，每个组平均分成 5个同质小组，每小组20人．将不同分数段的同质小组合并后，可形成5个组间同质、组内异质的大组，每组60人（见表 1）．

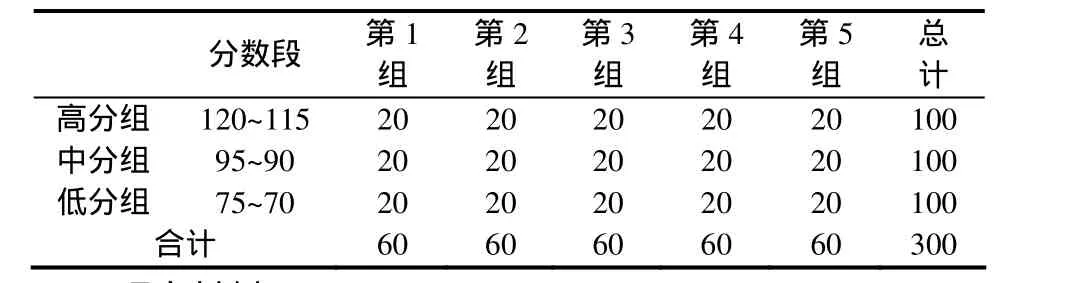
表1 样本分布情况

2.2 研究材料

研究材料是4组初中代数方程的应用题，每个题组由5道数学本质（所列方程）相同的应用题组成，在控制其它指标后，分别操纵语量（AW）、语境（CT）、语序（OW）和关键词（KW）的隐蔽程度中的一个指标．邀请高校专家、教研人员、中学教师和九年级优秀学生共计30人，对上述每组中5道应用题的难度进行排序，将统计结果作为该题的认定难度，由易到难依次记为1、2、3、4、5．

2.3 研究程序设计

研究采用4（语言指标）×5（认定难度）×3（学生成绩）×2（解题成绩和解答时间）的混合设计．把上述 20道试题分成5组，每组试题在4个指标对应的题目中各选1道搭配而成，每题满分10分，由主试分别提供给5组学生．学生答题的同时，根据计时软件记录下每道题的完成时间，若其中某道试题思考时间超过15 min，直接停止解答．4道题全部完成后由主试收回试卷．评卷时重点关注方程（组）布列的正确与否，给方程（组）中每个子部分都予赋分．测试所得数据用SPSS19.0统计软件包进行处理和分析，测试后选取被试的10%进行访谈，以了解他们解题时的思维方式和心历路程．

3 结果与分析

3.1 不同语量的问题对解题结果的影响

3.1.1 不同语量问题的均值比较

对 AW 题组的测试成绩和解题时间进行均值分析（见表2）．结果表明：AW-1至AW-4的测试成绩呈递减趋势、解题时间呈递增趋势，而AW-5由于呈现方式的变化与前4道题的情况有所不同．

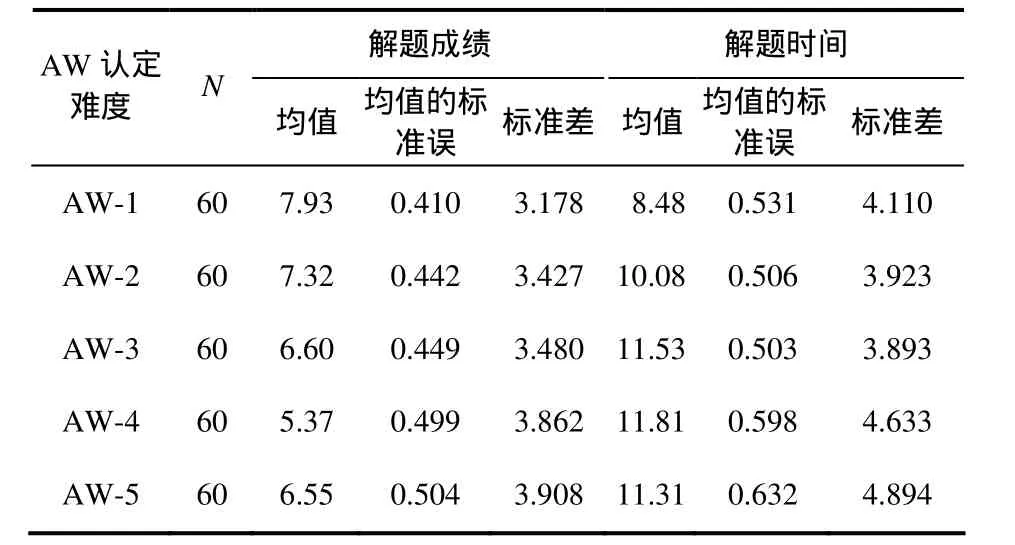
表2 语量（AW）测试成绩和解题时间均值概述

3.1.2 不同语量问题的方差比较

对 AW 题组的测试成绩和解题时间进行方差分析（见表3），结果显示：测试成绩主效应显著，F＝4.324，p＜0.01，表明不同语量试题对解题成绩的影响极为明显；解题时间主效应显著，F＝6.116，p＜0.001，表明不同语量试题对解题时间的影响非常明显．

表3 语量（AW）测试成绩和解题时间方差分析

对 AW 题组的测试成绩和解题时间按不同分数段学生进行方差分析（见表 4），结果显示：不同语量的问题对低分组解题成绩的影响显著，对高分组和中分组解题时间的影响非常显著．表明随语量增加，数学水平较高和数学水平中等学生的解题时间会明显增长，而数学水平较低学生的解题成绩会明显下降．

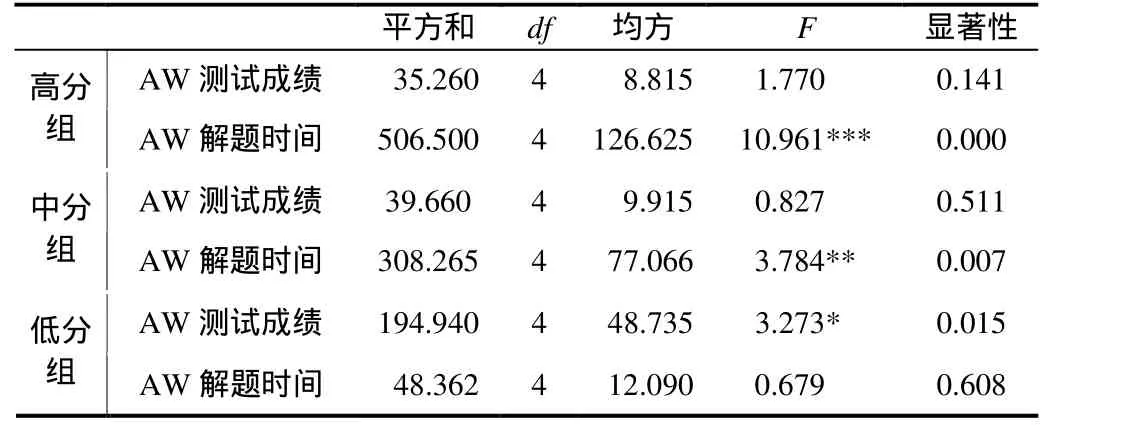
表4 不同水平学生语量（AW）测试成绩和解题时间方差分析

3.1.3 不同语量问题的相关性比较

将 AW 题组的测试成绩与学生分组的初始成绩进行相关分析（见表 5），结果显示：不同语量试题的测试成绩与学生分组成绩的相关性均很强，其中AW-3和AW-4的相关性尤为明显．表明不同语量问题的解题成绩能够较好地反映学生的实际数学水平，而大语量问题则具有更高的鉴别性．

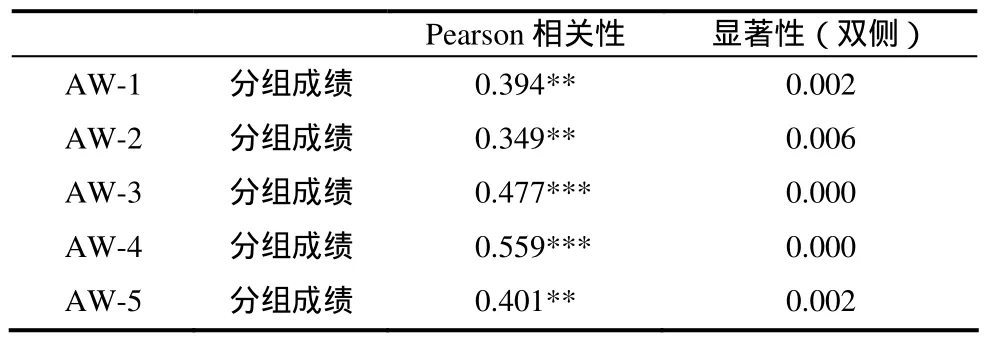
表5 语量（AW）测试成绩与学生分组成绩的相关性分析

3.2 不同语境的问题对解题结果的影响

3.2.1 不同语境问题的均值比较

对CT题组的测试成绩和解题时间进行均值分析（见表6）．结果表明：CT-1至CT-5的测试成绩呈递减趋势、解题时间整体上呈递增趋势．

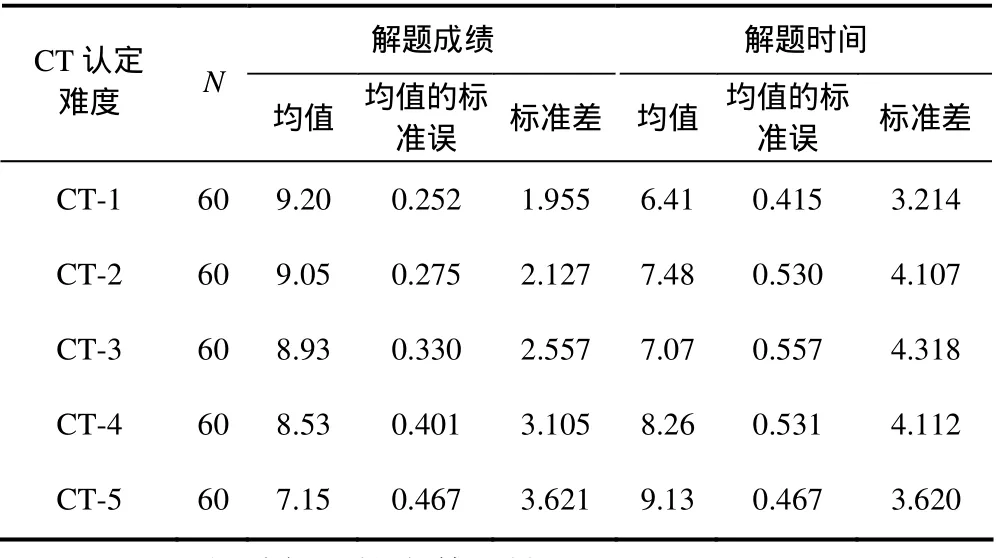
表6 语境（CT）测试成绩和解题时间均值概述

3.2.2 不同语境问题的方差比较

对CT题组的测试成绩和解题时间进行方差分析（见表7），结果显示：测试成绩主效应显著，F＝5.533，p＜0.001，表明不同语境试题对解题成绩的影响极为明显；解题时间主效应显著，F＝4.397，p＜0.01，表明不同语境试题对解题时间的影响非常明显．对CT题组的测试成绩和解题时间按不同分数段学生进行方差分析（见表 8），结果显示：不同语境的问题对中分组解题成绩的影响非常显著．表明随语境变化，数学水平中等学生的解题成绩会明显不同．

表7 语境（CT）测试成绩和解题时间方差分析

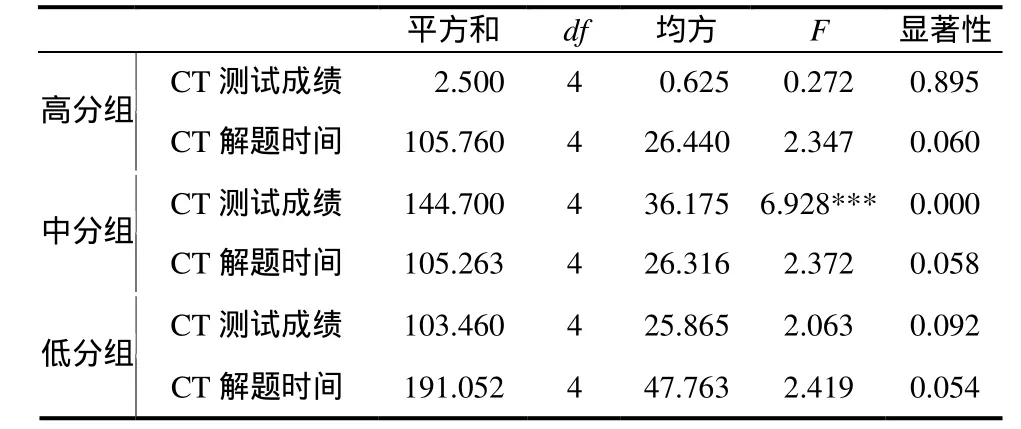
表8 不同水平学生语境（CT）测试成绩和解题时间方差分析

3.2.3 不同语境问题的相关性比较

将CT题组的测试成绩与学生分组的初始成绩进行相关分析（见表9），结果显示：CT-2至CT-5的相关性均较显著，其中CT-5的相关性尤为明显．表明不同语境问题的解题成绩能够较好地反映学生的实际数学水平，而复杂语境问题则具有更高的鉴别性．

3.3 不同语序的问题对解题结果的比较

3.3.1 不同语序境问题的均值比较

对 OW 题组的测试成绩和解题时间进行均值分析（见表10）．结果表明：OW-1至OW-5的测试成绩整体上呈递减趋势、解题时间呈递增趋势．

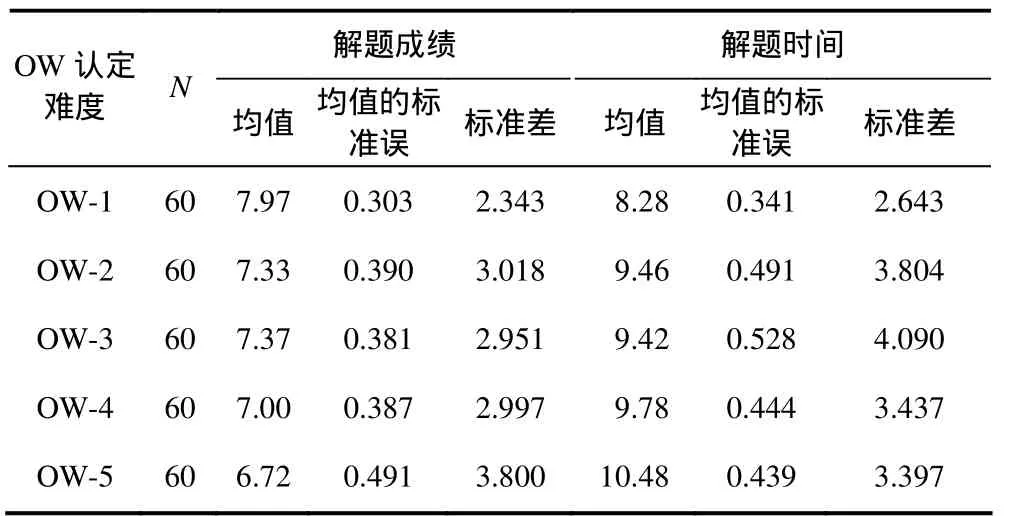
表10 语序（OW）测试成绩和解题时间均值概述

3.3.2 不同语序问题的方差比较

对 OW 题组的测试成绩和解题时间进行方差分析（见表11），结果显示：测试成绩主效应不显著，F=1.408，p＞0.05，表明不同语序试题对整体解题成绩的影响不够明显；解题时间主效应显著，F=3.072，p＜0.05，表明不同语序试题对解题时间的影响明显．对 OW 题组的测试成绩和解题时间按不同分数段学生进行方差分析（见表12），结果显示：不同语序的问题对高分组解题成绩的影响显著，对3个组解题时间的影响均极为显著．表明随语序变化，学生解题时间会随之增长，而数学水平较高学生的解题成绩会明显不同．

表11 语序（OW）测试成绩和解题时间方差分析

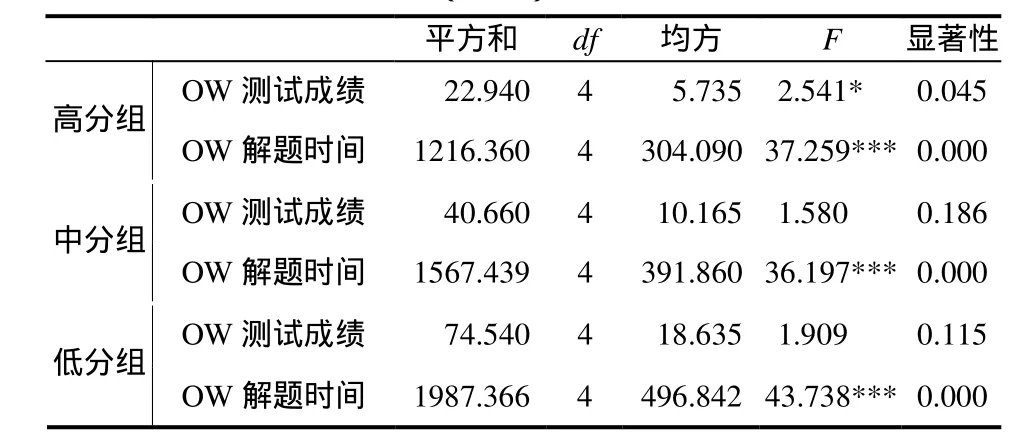
表12 不同水平学生语序（OW）测试成绩和解题时间方差分析

3.3.3 不同语序问题的相关性比较

将 OW 题组的测试成绩与学生分组的初始成绩进行相关分析（见表13），结果显示：OW-1至OW-5的相关性均极为显著，其中OW-3、OW-5的相关性尤其明显．表明不同语序问题的解题成绩能够较好地反映学生的实际数学水平，而复杂语序问题则具有更高的鉴别性．

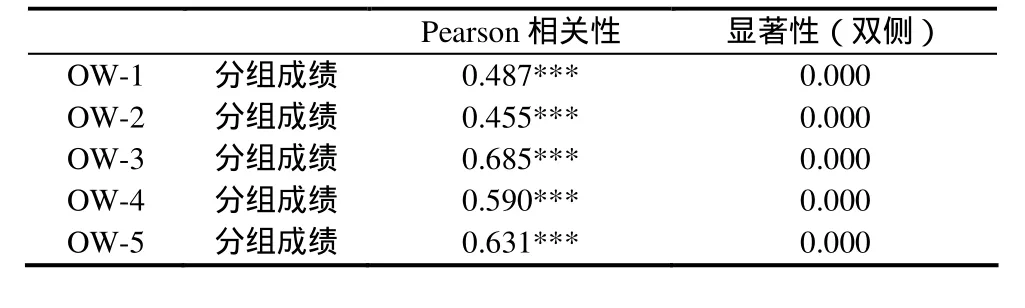
表13 语序（OW）测试成绩与学生分组成绩的相关性分析

3.4 关键词隐蔽程度不同的问题对解题结果的比较

3.4.1 关键词隐蔽程度不同问题的均值比较

对 KW 题组的测试成绩和解题时间进行均值分析（见表14）．结果表明：KW-1至KW-5的测试成绩呈递减趋势、解题时间整体上呈递增趋势．

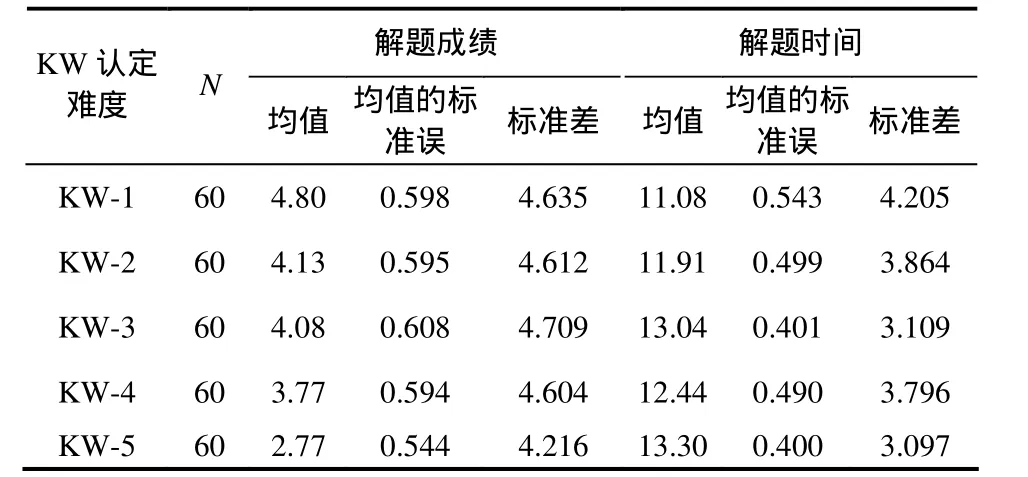
表14 关键词隐蔽程度（KW）测试成绩和解题时间均值概述

3.4.2 关键词隐蔽程度不同问题的方差比较

对 KW 题组的测试成绩和解题时间进行方差分析（见表15），结果显示：测试成绩主效应不显著，F=1.588，p＞0.05，表明关键词隐蔽程度不同的试题对整体解题成绩的影响未达到显著水平；解题时间主效应显著，F=3.617，p＜0.01，表明关键词隐蔽程度不同的试题对解题时间的影响非常显著．

表15 关键词隐蔽程度（KW）测试成绩和解题时间方差分析

对 KW 题组的测试成绩和解题时间按不同分数段学生进行方差分析（见表16），结果显示：关键词隐蔽程度不同的问题对中分组解题成绩的影响显著．表明随关键词隐蔽程度的变化，数学水平中等学生的解题成绩会明显不同．

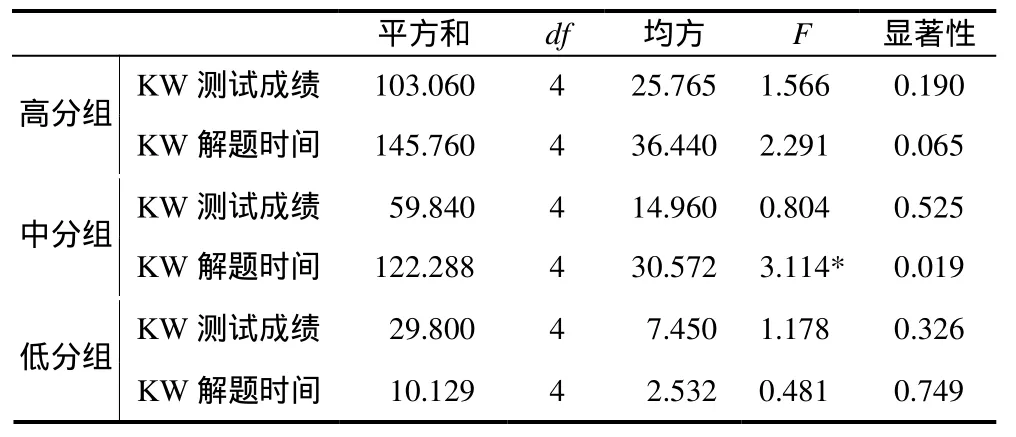
表16 不同水平学生关键词隐蔽程度（KW）测试成绩和解题时间方差分析

3.4.3 关键词隐蔽程度不同问题的相关性比较

将 KW 题组的测试成绩与学生分组的初始成绩进行相关分析（见表17），结果显示：KW-1至KW-5的相关性均极为显著，其中KW-4的相关性尤其明显．表明关键词隐蔽程度不同问题的解题成绩能够较好地反映学生的实际数学水平，而关键词隐蔽程度较高的问题则具有更高的鉴别性．

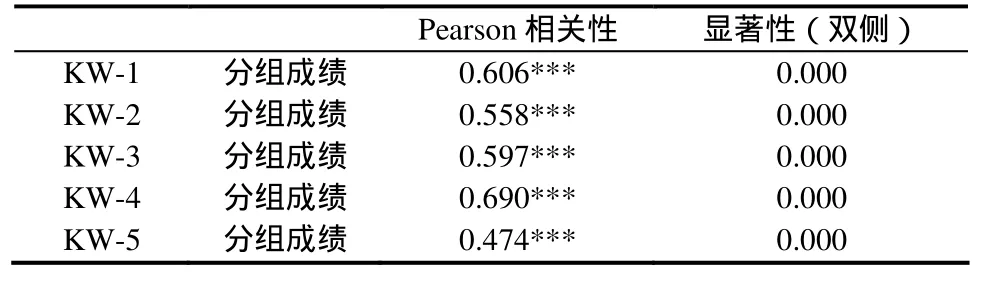
表17 关键词隐蔽程度（KW）测试成绩与学生分组成绩的相关性分析

4 讨 论

4.1 语量对代数应用问题解题的影响

研究表明，语量对学生解答代数应用题的效果影响明显，大语量问题通常会使学生的解题时间增长，而解题成绩下降．对于数学本质相同的问题，学困生与学优生相比更容易受到语量的影响．

导致大语量问题解题效果下降的一个原因是，随着题目中语量的增加，分布其中的数量与数量关系会变得分散．正是语量的这种“稀释”作用，使学生特别是学困生提取有效信息的难度增大．Sweller等人提出的认知负荷理论认为，解题者必须首先集中精力对两种信息进行加工，一种是正确解题所必需的信息，另一种是所谓的多余信息．苏帆[15]也提出，初中生感知能力的整体性差而选择性强，会导致解答应用问题时不能有效地关注有效信息，产生认知障碍．冯虹[14]等人在代数应用题解题过程的眼动研究中，发现学优生在表征关键信息时的眼动模式与学困生差异显著．学优生对应用题中关键信息的关注时间较长，学困生对题目的注视则比较盲目，而语量的增大无疑会加剧这种状况，从而影响他们的解题效果．

导致大语量问题解题效果下降的另一个原因是心理状态．当面对大量文字时，学生会主观上认为该题难度较大，直接影响其解答的信心和耐心，产生畏惧心理与胀饱心理．这一点，在测试后的访谈中明显地体现出来．特别是学困生，在文字超过200字时，厌倦和退缩的情绪较为严重．

研究也发现，带有配图和表格的试题（如 AW-5），虽文字仍较多但对解题的影响相对变小，这说明应用题的呈现方式对学生的解题水平具有影响．游旭群等[16]指出，从总体上讲，图形和图式呈现下的解题水平高于文字呈现下的解题水平，即有一定视觉提示的问题呈现方式促进了学生解题水平的提高．一方面，图表的直观性有助于学生更好地理解问题情境，另一方面，图表还会将一些原本分散的条件集中起来，一定程度上削弱语量对关键信息的“稀释”作用．由此可见，降低语量影响的一个有效策略是，使学生有意识地借助图表集中数量、简化问题．

4.2 语境对代数应用问题解题的影响

研究表明，不同的语境对学生解答代数应用题的效果影响明显．也就是说，不同的问题情境给学生带来的感受是不同的．从试验结果看，同样是两个数量相乘的关系，以矩形面积为背景的问题就比以行程为背景的问题容易许多，其中数学水平中等的学生体现尤为明显．

何纪全[17]在研究应用题的情节结构时，要求学生用两个数字自由编题，并对所编题目进行情节成分分析，结果显示：在被分成的8个情节类型中，小学高年级学生编写的应用题，取材于直接生活经验、集体或社会的活动、工农业生产活动、商品购销、几何或理化科学、无运算术语的文字题以及年龄时间等7个方面的问题都有出现，但唯独没有涉及行程问题的情节出现．

学生解决行程问题的困难，不在于对数量关系“速度×时间＝路程”的理解．事实上从小学开始，多数学生对这一关系早已谙熟于胸．但行程问题，由于其描述的是一个运动变化过程，所以学生需要在头脑中构建更为复杂的、不断变换的场景，从而增加了其理解问题的难度．而当遇到以矩形为背景的问题时，学生更容易在读取文字的同时形成视觉表象，这种表象是直观的、静止的，学生能够在头脑中能够清晰地“看”到．赖颖慧[18]认为，视觉化表征在代数应用题的信息加工过程中至关重要，它有助于主体快速形成清晰的问题空间，把握应用题的数量关系．

在应用题教学中是以类型化为重点，还是以分析数量关系为重点，在实践中一直存有争议．施铁如[12]认为，两者不是对立的．突破类型效应这个瓶颈的关键，是学生需要建构起置于具体问题情境之上的更具概括性的数量关系模型．例如，张庆林[19]的研究就显示，如果学生能够把有些应用题分别使用的“工作效率×工作时间=工作总量”、“速度×时间=路程”、“单价×数量=总价”等关系式归纳为一个更概括的关系式“单位量×单位数=总量”，解题能力便得到提高．

4.3 语序对代数应用问题解题的影响

在前面的研究中可以看出，语序对学生解代数应用题的成绩有一定程度的影响，但不够显著；而其对学生解代数应用题时间的影响相对比较明显．这说明，学生在解决语序混乱的问题时，会花更多的时间去理解语句与语句的关系，辨别条件的使用次序．

语序的这种影响是由学生使用的应用题表征策略引起的．许多研究显示[20~22]，应用题表征存在两种基本策略：直接转换策略和问题模型策略．直接转换策略指当面对应用题时，主体并不过多考虑问题表述中的语义和词序是否符合正常的逻辑顺序，只关注题目中的数字和关键词，对数字进行加工．问题模型策略指当面对应用题时，主体首先试图理解问题情境和条件间的关系，建立问题的情境模型，然后制订相应的解题计划．在测试后的访谈中发现，不能成功解题者思考问题的过程正是较多地使用了直接转换策略．

陈英和[21]等人的研究支持了这个观点，他们的研究发现，学生对按正向逻辑顺序表述的题目（一致型问题）的反应时间要显著少于按负向逻辑顺序对题目进行表述的题目（不一致型问题）．从学优生的自我报告来看，使用问题模型策略的学生要多于使用直接转换策略的学生．

因此，想要有效改善语序对解题带来的不利影响，应致力于改变学生应用题的表征策略，促使惯于使用直接转换策略思考问题的学生向问题模型策略转变．

4.4 关键词的隐蔽程度对代数应用问题解题的影响

研究中发现，关键词的隐蔽程度对学生解代数应用题的成绩也有一定程度的影响，但不够显著；但其对学生解题时间的影响却非常显著．这说明，大多数学生面对关键条件隐蔽性较强的应用题时，会花费大量时间去寻找和发掘这些列方程所需的条件．

何纪全[17]的研究显示，学生分辨应用题中多余已知数的难度，呈现明显的层次性——对与题目无关的多余已知数，最容易剔除；对于虽与题目无直接数量关系，但又是丰富题目的情节所必要的已知数，则比较难些；对于与题目数量关系有关但不决定运算的多余已知数，则更难判断；对于用不同方法解题时，有时有用而有时多余的已知数，则只有很少的学生能根据不同情况做出判断．

学生识别关键词的能力与认知发展的水平有着密切的联系，但也与人们日常对应用题的训练方式不无关系．史宁中[23]指出，长期以来，大家对方程应用习题的设计、处理太理想化了，几乎直接变成数学符号了，这不是真正意义上的应用题．

因此，要克服关键词隐蔽程度对解题的影响，就要使学生能够更多地接触到具有真实信息的问题，“到大海里学游泳”，不断增强其辨识能力，提高其认知水平．

5 结论与建议

（1）语量对代数应用题的解题效果具有显著影响．欲改善其负效应，教学中应使学生克服畏惧心理，有意识地运用图表等更为直观的方式表征问题；

（2）语境对代数应用题的解题效果具有显著影响．欲改善其负效应，教学中应使学生建构脱离具体情境的、上位的数量关系模型；

（3）语序对代数应用题的解题效果具有一定影响．欲改善其负效应，教学中应努力改变学生应用题的表征策略；

（4）关键词的隐蔽程度对代数应用题的解题效果具有一定影响．欲改善其负效应，教学中应创造条件使学生更多地接触真正的现实问题．

[1] 郭兆明，宋宝和，张庆林．数学应用题图式层次性研究[J]．数学教育学报，2006，8（3）：27-30．

[2] 周新林，张梅玲．加减文字题解决研究概述[J]．心理科学进展，2003，（6）：642．

[3] 康园园．近年国内小学数学应用题解决研究的评述[J]．成都大学学报，2008，（10）：20-23．

[4] Hudson T. Correspondences and Numerical Differences between Disjoint Sets [J]. Child Development, 1983, (54): 84-90.

[5] CumminsD D. Children’s Interpretations of Aritlunetic Word Problems [J]. Cognition and Instruction, 1991, 8(3): 261-289.

[6] 周治金，陈永明．算术应用题理解的几个理论模型[J]．教育研究与实验，2001，（2）：53-58．

[7] 李陆平．数学应用题语言理解的探究[J]．现代教育科学，2011，（6）：10-11．

[8] 辛自强．数学中的阅读理解[J]．教育科学研究，2004，（9）：49-51．

[9] 张拓书．语文能力低是小学生学习应用题难的重要原因[J]．内蒙古师大学报，1999，（4）：144-147．

[10] 鲍建生，周超．数学学习的心理基础与过程[M]．上海：上海教育出版社，2009．

[11] 刘四新．初中生应用题解题困难分析[J]．数学通报，2007，（7）：19-21．

[12] 施铁如．解代数应用题的认知模式[J]．心理学报，1985，（3）：296-303．

[13] 陈英和，仲宁宁，赵宏，等．小学2~4年级儿童数学应用题表征策略对其解决不规则问题影响的研究[J]．心理科学，2005，（6）：1 314-1 317．

[14] 冯虹，阴国恩，陈士俊．代数应用题解题过程的眼动研究[J]．心理科学，2009，（5）：1 074-1 077．

[15] 苏帆，韩冰．初中生解决数学应用问题的认识障碍研究综述[J]．桂林市教育学院学报，2000，（12）：86-88．

[16] 游旭群．小学生数学应用题解题水平影响因素的实验研究[J]．心理学探新，2006，（4）：63-67．

[17] 何纪全．关于小学生对应用题结构认知发展的初步研究[J]．心理学报，1988，（1）：8-14．

[18] 赖颖慧，陈英和．代数应用题视觉化表征的理论模型及影响因素[J]．心理科学进展，2010，（1）：75-83．

[19] 张庆林，杨东．高效率教学[M]．北京：人民教育出版社，2002．

[20] 路海东，董妍．小学生表征数学应用题策略的实验研究[J]．心理发展与教育，2003，（1）：60-63．

[21] 陈英和，仲宁宁，田国胜，等．小学2~4年级儿童数学应用题表征策略差异的研究[J]．心理发展与教育，2004，（4）：19-24．

[22] 仲宁宁，陈英和，王明怡，等．小学二年级数学学优生与学困生应用题表征策略差异比较[J]．中国特殊教育，2006，（4）：63-68．

[23] 史宁中，孔凡哲．方程思想及其课程教学设计——数学教育热点问题系列访谈录之一[J]．课程·教材·教法，2004，（9）：27-31．