一元二次不等式的特征对其解法迁移的影响

连四清，佘 岩，王 欣

（首都师范大学 数学科学学院，北京 100048）

1 问题提出

研究者经常观察到学生通过考察教材或教师提供的有解答步骤的例题来获得新问题的解答，或者翻看自己已经解决过的问题来获得新问题的解答．这种应用学习过的有解样例或解决过的问题来获得新问题解决的过程，称为类比迁移过程．其中，有解答的样例或已解决过的问题称为源问题，而要解决的新问题称为靶问题．

自20世纪90年代开始，研究者开始关注数学领域内的类比迁移问题，主要探索源问题和靶问题的相似性如何影响类比迁移的过程．通常情况下，研究者将源问题信息划分为表面信息和结构信息，其中表面信息是指涉及的事物、情节、形式等信息，而结构信息是指问题解决涉及的内在的原理和关系[1~3]．如，解决问题过程中应用的数学公式、数学方法等都属于数学问题的结构信息，而与此无关的信息都是表面信息．在问题相似性的划分方法上，研究者基本上沿用了非数学领域的问题的相似性分类方法，即将源问题和靶问题相似性划分为表面相似（surface similarity）和结构相似性（structure similarity）[1~4]．问题的表面特征是指这种特征的变化不会影响问题内在原理的应用，而结构特征是指这种特征的变化将影响到问题的解决过程中应用的原理，相似性就是指这些特征之间的关系[2]．如果特征相同，则称相似；如果这些特征不同，则称不相似．

Ross等人首先对排列组合问题的表面特征进行了更细致的分解，揭示了排列组合问题的表面特征如何影响源问题的选取和匹配过程[1，5~7]．之后，莫雷[8]等人对工效问题和运输问题的表面特征进行了更加细致的分解，如将表面特征进一步分解为事件属性和事件类型，实验结果表明：靶问题的事件属性发生较大变化，尤其是发生相反变化时，表面特征的相似性对原理的运用会产生明显的影响．这种影响体现在被试按照样例的对应模式形成运用原理的定势上．因此，当源问题和靶问题的对象对应相似或一致时，表面特征就会促进类比迁移，而对象对应不一致时，就会起干扰作用．之后，系列研究通过细化表面特征来探索影响类比迁移的因素[9~11]．在样例变异性研究中，研究者也应用这种特征是否相似来操作样例的变异性[11~13]．

宁宁和喻平（2010）探索了用解题步骤来刻画源问题和靶问题相似性的操作方法，即用解题步骤的相似性来衡量样例变异水平的高低，结果表明：对近迁移而言，样例的变异性水平对其影响不大，但对于中等迁移和远迁移而言，样例的变异水平有显著影响[14]．这是一种有价值的尝试，也是一次新的探索．其实，文字问题（或应用题）与纯数学问题（或非文字问题）的特征有较大差异，如应用题往往有背景，或者事件等与其所蕴含的数学关系或结构无关，如工程问题、行程问题表明的都是数学关系“c=a×b”，但是对工程完成和行程的过程及情境都是表面的．然而，与文字问题不同，纯数学问题中更多地应用符号语言或图形语言来描述数学关系．有时候符号的变化并不必然带来解法、公式应用或步骤变化，也并不必然干扰原来方法的实施．如，方程中的系数是表面的还是结构的？就十字相乘法而言，若将“ - 1”改为“ - 1 9 99”，十字相乘法就很难实施；但是如果将其改为“ - 5 ”，十字相乘法仍然可以实施．但是就求根公式而言，系数的改变只有改变方程是否有实根，以及求根运算的复杂性，并不干扰方法的迁移．也就是说，有时候教师很难区分问题的表面特征和结构特征．为此，研究者尝试抽取一元二次不等式的一些特征，应用特征的相似性来刻画源问题和靶问题的相似性，从而探索一元二次不等式的特征是否影响其解法的迁移．

2 实验方法

被试：从北京市市区某一普通高中学校一年级（共240人）按学优生、学中生和学困生3个层次进行分层随机抽样68人作为被试．实验前，被试学习过二次函数，一元二次方程有关知识，但是没有学习过一元二次不等式及其解法等有关知识．

材料：实验材料有一元二次不等式及其解法的学习材料和测试材料两种．其中，学习材料由一个例题“解一元二次不等式：2x2-3x-2＞0”，详细解答步骤，说明二次函数和不等式之间关系及其图象，并就一元二次不等式解法的步骤进行小结．如“解一元二次不等式，要结合二次函数图象，既要考虑开口的方向，又要通过判别式考查函数与x轴交点的个数，从而写出不等式的解集．”测试材料有甲乙两种，甲种是由12道如“的不等式组成，乙种是由 12道如“的不等式组成．在两种测试材料中，2（两种二次系数的正负情况：（3种判别式值的类型：等6种问题特征组合中的每一种特征的不等式有两个．如，不等式“- x2+x-2＞0”是测试材料甲中的问题，其特征为“二次项系数a＜0”、“判别式Δ<0”．用拉丁方安排每种测试材料中的数学题顺序以控制顺序效应．

程序：学生用学习材料学习如何解一元二次不等式，10分钟后主试将学习材料回收．之后，主试将测试材料随机分配给被试，要求被试在30分钟内完成求解一元二次不等式的解集的问题．其中，解决测试材料甲中的被试36人，乙中有32人．

评分标准：解二次不等式分3步：判断二次项系数正负，求判别式，判断根的情况和求根，画出草图并观察草图得到二次不等式解集．为了考察被试能否应用上述步骤，评分标准如下：能够判定二次项系数正负2分，计算判别式的给3分，能够判断实根个数情况和求出一元二次方程的根3分，画出对应二次函数草图并写出解集（或写出不等式）的给2分，每题共计10分，满分120分．因判别式和求根计算错误影响后续解题步骤和答案不扣分，以考察解二次不等式的方法的迁移程度．以被试在具有这些特征的不等式迁移成绩的平均分计算被试内变量组合对应的因变量，最高分10分．

3 实验结果

对数据进行处理之前，以两个具有同样特征的迁移成绩的平均值作为因变量数据．两种不等式类型（大于零和小于零）、两种二次项系数的正负情况（a>0，a<0）、3种判别式值的类型（Δ>0，Δ<0，Δ=0）特征的一元二次不等式解法的迁移成绩进行描述性统计，结果如表1所示．

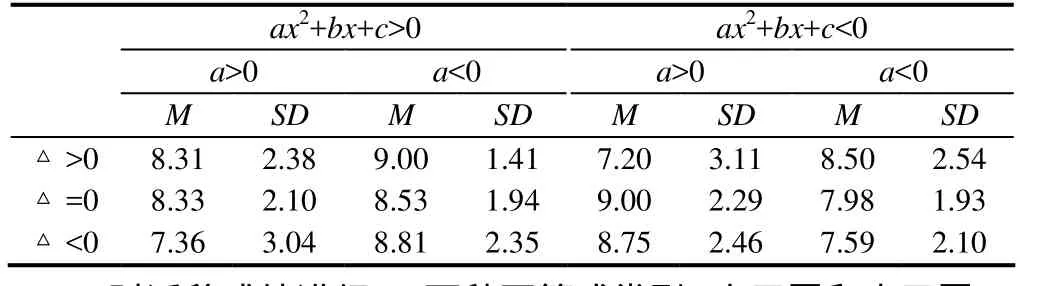
表1 问题迁移得分描述性统计结果

对迁移成绩进行2（两种不等式类型：大于零和小于零）×2（两种二次项系数的正负情况：a>0，a<0）×3（3种判别式值的类型：Δ>0，Δ<0，Δ=0）重测方差分析，其中两种不等式类型为被试间因素，两种二次项系数和3种判别式值均为被试内因素．结果表明：（1）不等式类型的主效应不显著（F(1, 66)=0.024，p=0.876），这说明：两种不等式类型上的迁移没有显著差异．（2）二次项系数主效应不显著（F(1, 66)=2.809，p=0.098>0.05）．这说明：二次项系数大于0还是小于0对二次不等式解法迁移没有显著影响；二次项系数与不等式类型两因素交互作用不显著（F(1, 66)=2.264，p=0.13705.0＞）．（3）判别式主效应不显著（F(2, 132)=0.304，p=0.738>0.05）．这说明，判别式对二次不等式解法迁移没有显著影响；判别式与不等式类型两因素交互作用处于边缘水平（F(2, 132)=3.044, p=0.051），这说明，判别式与不等式类型在一定程度上交互影响解法的迁移．（4）二次项系数、判别式交互效应显著（F(2, 132)=5.321，p=0.006<0.05）．这说明：二次项系数的正负和判别式交互影响一元二次不等式的解法的迁移；（5）二次系数、判别式与不等式类型三因素交互作用显著（F(2, 132)=3.599，p=0.030）．这说明，二次项系数、判别式、判别式类型共同交互影响一元二次不等式解法的迁移．

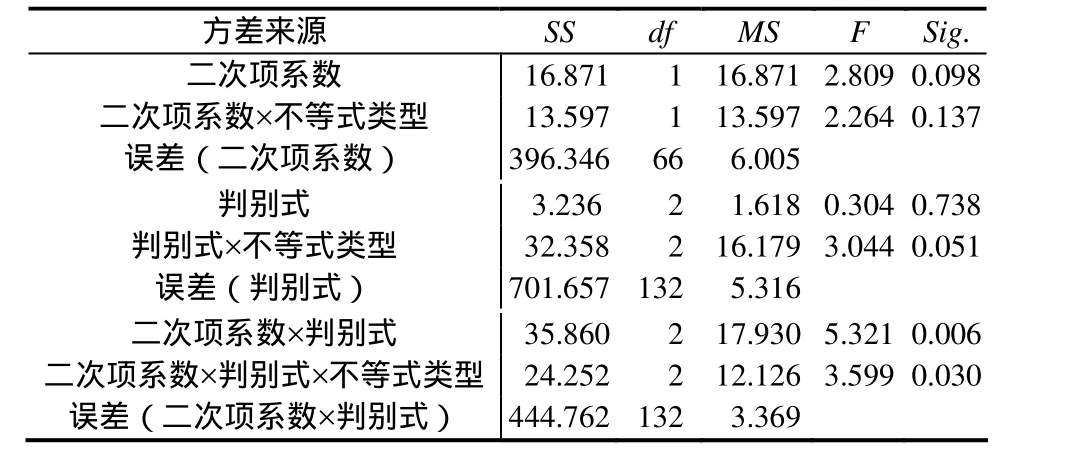
表2 迁移成绩的2×2×3重测方差分析结果

进一步分析表明：就不等式 a x2+ b x+c＞0而言，在Δ>0和Δ=0的条件下，解法在a＞0与a＜0的二次不等式上的迁移成绩没有显著差异a＞0的不等式解法的迁移成绩显著低于说明，对于不等式 a x2+ b x+c＞0而言，解法迁移到“解集为Φ的不等式”上较迁移到“解集为R的不等式”上更为困难．对于不等式 a x2+ b x+c＜0而言，在Δ>0和Δ=0的条件下，二次项系数的正负不影响方法的迁移的条件下，a＞0条件下的不等式迁移成绩显著高于a＜0的迁移成绩（F(1, 35)=7.30，p<0.05），这说明：对于不等式ax2+ b x+c＜0而言，将解法迁移到“解集为Φ的不等式”上较迁移“解集为 R的不等式”上更为困难．总的来说，无论是 a x2+ b x+c＞0还是 a x2+ b x+c＜0，不等式类型、二次项系数和判别式的三因素交互作用体现在一元二次不等式解法迁移较容易迁移到“解集为 R的不等式”上，而迁移到“解集为Φ的不等式”则更为困难，其他解集类型的不等式的迁移没有显著差别．

4 讨 论

实验发现：二次不等式类型、二次系数和判别式等 3个特征的主效应均不显著，而在3个因素中，不等式类型与判别式，二次项系数与判别式等两个两因素的交互作用、以及三因素交互作用显著．这说明，3个因素对二次不等式解法的迁移的影响并不是彼此独立的．进一步分析表明，在两种不等类型（ a x2+ b x+c＞0和ax2+ b x+c＜0）中，二次项系数和判别式对不等式解法的迁移产生了不同的影响，这种影响具体表现在：第一，解集为 ( m , n)（ m ＜ n ）型或(-∞, m) ∪(n,+∞)型，二次项系数的正负、判别式与零的大小关系对解法迁移没有显著影响．也就是在学习了不等式ax2+ b x+c＞0（a＞0，Δ>0）后，学生可以将解法迁移到除不等式 a x2+ b x+c＞0（或 a x2+ b x+c＜0）解集为Φ的情形之外的其他情形中；第二，相比较解集为 R集的不等式而言，解法更难迁移到解集为Φ的不等式上．这些结果说明，在二次不等式解法迁移的过程中，二次不等式的二次项系数、判别式的正负和不等式类型在不等式解集为Φ的条件下影响到方法迁移，而其他条件下这些不等式的特征不影响解法的迁移．

研究者认为：相比较而言，二次不等式的解法迁移到“解集为Φ的二次不等式上”并不能直接得到问题的解答，而需要对解法的某些步骤进行更为精细的加工．如，结合二次函数 f ( x)= a x2+bx+c图象，归纳概括得到“没有实数满足不等式 a x2+ b x+c＜0”，解集和空集概念得到不等式解集为Φ等．相反，当a＞0，Δ<0时，二次函数图象在x轴上方，观察图象，被试能够“看”出“不等式解集为R”．因此，当不等式的解集为R时，解法迁移会更容易．

显然这里的研究结果部分支持“靶问题和源问题越相似，则源问题的解法迁移到靶问题的效果越好”的结论[1~10]．按照划分表面特征和结构特征的理论观点，不等式类型、二次项系数和判别式是表面特征，或者是结构特征，二者只居其一．这些特征要么对迁移没有影响，要么有显著影响，其交互性体现在特征越相似其迁移效果越好，越不相似迁移效果越差．但是，不等式类型、二次项系数和判别式对解法的迁移都没有产生非常显著的影响，但是它们存在显著的三因素交互作用．因此，这里的研究结果并不完全支持与已有的观点．

其实，在纯数学问题（非文字问题或应用题）中，很难把问题的特征归结于表面特征还是结构特征．如，对于数学问题“已知等比数列 {an}， a1+ a2+a3=3，a4+ a5+a6=-81，求lim Sn”．解决这个问题时，可以列出

n → ∞

关于等比数列首项和公比的方程组，即

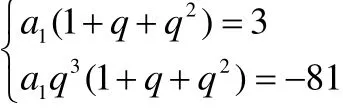
5 结 论

二次不等式类型、二次系数和判别式等3个特征的主效应均不显著，而在3个因素中，不等式类型与判别式，二次系数与判别式等两个两因素的交互作用、以及三因素的交互作用显著．这说明，在解集为Φ的不等式上，3个因素共同干扰了解法的迁移．

[1] Ross B H. This Is Like That: The Use of Earlier Problems and Separation of Similarity Effects [J]. Journal of Experimental Psychology: Learning, Memory, and Cognition, 1987, 13(3): 629-639.

[2] Holyoak K J, Koh K. Surface and Structural Similarity in Analogical Transfer [J]. Memory & Cognition, 1987, 15(4):332-340.

[3] Reed S K. A Structure-Mapping Model for Word Problems [J]. Journal of Experimental Psychology: Learning, Memory,and Cognition, 1987, 13(1): 124-139.

[4] Gentner D, Markman A B. Structure Mapping in Analogy and Similarity [J]. American Psychologist, 1997, 52(1):45-56.

[5] Ross B H. Distinguishing Types of Superficial Similarities: Different Effects on the Access and Use of Earlier Problems[J]. Journal of Experimental Psychology: Learning, Memory, and Cognition, 1989, 15(2): 456-468.

[6] Ross B H, Kennedy P T. Generalizing from the Use of Earlier Examples in Problem Solving [J]. Journal of Experimental Psychology: Learning, Memory, and Cognition, 1990, 16(1): 42-55.

[7] Ross B H, Kilbane M. Effects of Principle Explanation and Superficial Similarity on Analogical Mapping in Problem Solving [J]. Journal of Experimental Psychology: Learning, Memory, and Cognition, 1997, 23(2): 427-440.

[8] 莫雷，刘丽虹．样例表面内容对问题解决类比迁移过程的影响[J]．心理学报，1999，（3）：313-321．

[9] 莫雷，唐雪峰．事件类型的相似性对原理运用的影响的实验研究[J]．心理科学，2001，（1）：5-8．

[10] 唐雪峰，莫雷．表面内容不同方面相似性对样例迁移的影响[J]．心理科学，2003，（4）：631-633．

[11] 刑强，莫雷．多重样例的变异性和编码对迁移影响的实验研究[J]．心理科学，2005，（6）：1 382-1 387．

[12] 罗蓉，胡竹菁．相似性组合及元认知监控对问题类比推理的影响研究[J]．心理与行为研究，2010，（4）：246-251．

[13] 连四清，曾辉．自我解释对等差数列概念和通项公式远近迁移的影响[J]．数学教育学报，2011，20（4）：23-25．

[14] 宁宁，喻平．多重变异性数学样例对迁移影响的初步研究[J]．数学教育学报，2010，19（6）：50-52．