基于直驱永磁风力发电系统中最大风能跟踪的实现

李勇，朱晓青，黄鹰

（湖南工业大学电气与信息工程学院，湖南株洲412007）

基于直驱永磁风力发电系统中最大风能跟踪的实现

李勇，朱晓青，黄鹰

（湖南工业大学电气与信息工程学院，湖南株洲412007）

研究贝兹原理关于永磁同步风力发电机的最大风能跟踪理论，提出了叶尖速比控制方法。介绍风力机的数学模型，以及最佳叶尖速比控制方法，构建永磁同步风力发电机的数学模型，继而利用Matlab/ Simulink软件对该模型进行仿真分析。仿真结果表明：本控制方法能快速准确地实现风能的最大跟踪。

最大风能跟踪原理；永磁同步发电机；风能利用率；叶尖速比的控制方法

0 引言

风能是一种新型清洁能源。风能的使用可优化未来的能源利用模式。当风速稳定时，风力发电机的空气动力性能极佳。但当遇到阵风、湍流和风剪流时，风力发电机叶片的工作效率会降低。因此，如何提高风能的利用率是风力发电的研究热点之一[1]。目前常用的最大风能跟踪控制方法主要有3种，即最佳叶尖速比法、功率反馈法和爬山搜索法。其中，功率反馈法和爬山搜索法需要测量风机固有特性，移植性不强。因此，本文提出了利用最佳叶尖速比控制方法来实现永磁同步风力发电机的最大风能跟踪。风力机只有在最佳叶尖速比下运行，才能输出最大机械功率。所以要使风力机输出最大机械功率，则必须使其按最佳叶尖速比关系运行。

本文先阐述了风力发电系统的基本原理、风力机的结构与组成以及贝兹理论，分析了最佳叶尖速比控制方法的原理，并在Matlab/Simulink环境下构建系统仿真模型，对其进行仿真分析。仿真结果说明该系统的追踪效果较为理想，实现了风力发电机的最大风能跟踪。

1 风力机的数学模型

贝兹（德国科学家）于1926年建立了风力机的第一个气动理论。贝兹理论的推出是基于以下几个假设：风力机没有轮毂，风力机的叶片为无穷多，当气流经过风轮叶面时是均匀的，气流的速度方向在经过风轮前后均为轴线方向[2]。

根据空气动力学知识，可以得出气流功率为

A为风力机扫过的面积；

V为风的速度。

叶片从气流中捕获风能的功率为

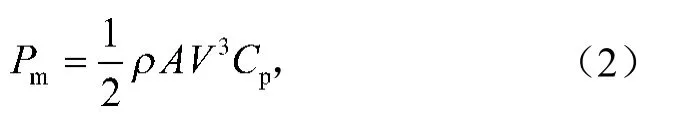
式中：Cp为风能利用系数。根据贝兹理论，风能利用系数Cp的最大值为0.59。风力机扫过的面积和空气密度都可认为是常量，因此，当风速一定时，功率Pm的大小只与风能利用系数Cp有关，即

由式（3）和式（4）可知，风能利用系数Cp与叶尖速比和风力机的桨距角为非线性关系。

2 最佳叶尖速比控制方法的原理

永磁直驱风力发电机组是风力机和永磁同步发电机直接相连，中间没有增速齿轮箱，因此，风力机的风速和永磁同步发电机的风速相同，即。为了控制风力机的速度来实现风能的最大捕获，本文采用最佳叶尖速比控制方法来控制永磁同步发电机的速度[3]。

图1 最佳叶尖速比控制方法Fig.1The optimal tip speed ratio control method

3 永磁同步风力发电机的数学模型简介

基于转子磁场定向矢量控制的零d轴电流控制，存在以下优点：第一，零d轴电流不会出现退磁现象；第二，算法简单易于实现，转矩与电流为线性关系，零d轴电流对隐极式发电机转速调速范围不受限制。通过坐标变换将静止坐标系下的三相电流变换成dq轴电流，再调节d轴电流，使d轴电流为零，这样定子电流中的q轴电流就可以全部用来产生电磁转矩，实现永磁直驱风力发电机的励磁与转矩的解耦。

要将三相静止坐标系ABC变换到两相旋转坐标系dq中，需要先将三相静止坐标系变换到两相静止坐标系中。两相静止坐标系中的坐标轴就与三相静止坐标系中的相重合，轴超前轴90度。这样就得到了两相静止坐标系。

式中：为坐标系中轴和d轴之间的夹角。

因此三相静止坐标系ABC变换到两相旋转dq坐标系的公式为：

永磁电机在两相旋转dq坐标系下的数学模型如下所示。

式（9）～（11）中：ud, uq分别为d轴和q轴电压；

id, iq分别为d轴和q轴电流；

Rs为永磁发电机每相定子绕组中的电枢绕组；

根据永磁同步电机理论，可得电机的运动方程为

式中：Tm为风力机输入的机械转矩；

Te为永磁同步电机的机械转矩；

电磁转矩方程为

式中：np为电机极对数；

Ld, Lq为dq轴同步电感；

采用id=0的控制策略，因此式（13）转化为

从电磁转矩方程可知，电磁转矩的大小只与q轴电流有关，而与d轴电流无关，真正实现了永磁直驱风力发电机的励磁与转矩的解耦。

4 最佳叶尖速比的仿真模型和仿真结果

本文选择一台60kW的永磁同步发电机，详细的电机参数如下：定子侧绕组电阻0.0065H，永磁体转子的磁链f=1.3Wb，空气密度为风力机的叶片半径R=2.5m，风力机的额定风速为7.5m·s-1。仿真试验进行到0.6s时，风速由7.0m·s-1变化为7.5m·s-1，检验风力机是否能对风能进行最大跟踪。

在实际工程中，应用最为广泛的调节器为比例-积分-微分（proportional-integral- differential，PID）控制器。其中，PID控制器的参数整定是控制系统设计的核心内容。PID控制器参数整定的方法很多,概括起来有两大类。一是理论计算整定法。它主要是依据系统的数学模型，经过理论计算确定控制器参数。这种方法所得到的计算数据未必可以直接用，还必须通过工程实际进行调整和修改。二是工程整定方法，它主要依赖工程经验，直接在控制系统的试验中进行，且方法简单、易于掌握，在工程实际中被广泛采用[7]。

通过工程整定方法选取合适的PI参数，可以得到较为理想的追踪效果，从而实现风能的最大跟踪。为了验证最佳叶尖速比控制方法的正确性，搭建了永磁直驱风力发电机的机侧仿真模型，如图2所示。

图2 最佳叶尖速比的仿真模型Fig.2The simulation model of optimal tip speed ratio

风能利用系数Cp的仿真波形如图3所示。

由图3可以看出，在0～0.6s时，风速为7.0m·s-1，Cp能迅速稳定在0.47附近；0.6s之后，风速变为7.5m·s-1时，Cp也能迅速稳定在0.47附近。这说明当风速变化时，风能利用系数能维持在最大值附近。

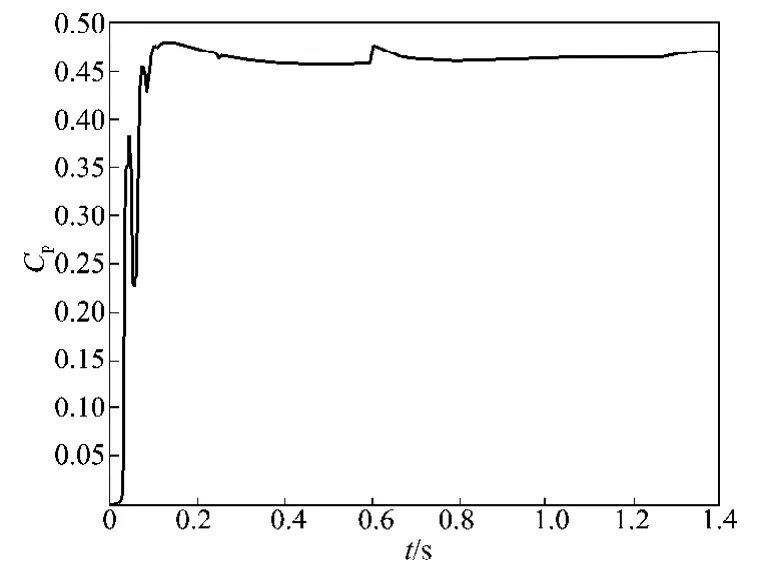
图3 风能利用系数波形Fig.3Waveform of wind energy utilization coefficients

叶尖速比的仿真波形如图4所示。

由图4可以看出，当风速变化时，叶尖速比能够迅速运行在最佳状态下。这说明风力发电机组跟踪了所建仿真模型的最佳功率曲线，能够实现实时对风能的最大捕获。

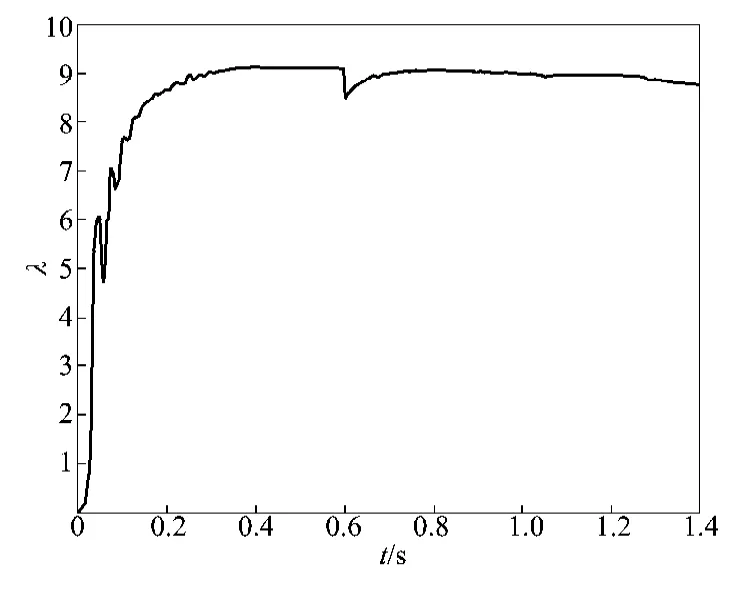
图4 最佳叶尖速比波形图Fig.4Waveform of optimal tip speed ratio

图5为永磁同步电机转速图。图6为永磁同步电机功率图。图7为d轴电流。图8为q轴电流。

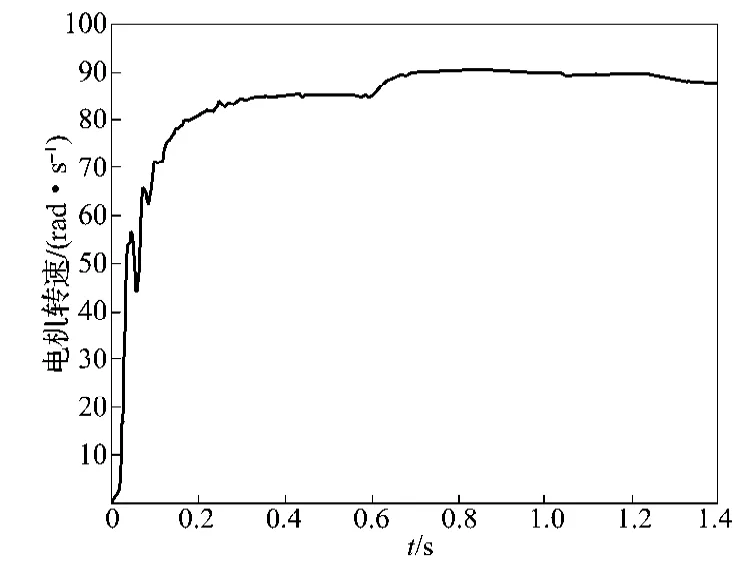
图5 永磁同步电机转速Fig.5The speed of permanent magnet synchronous motor

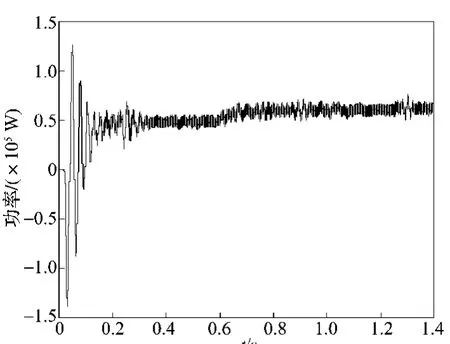
图6 永磁同步电机的功率Fig.6The power of permanent magnet synchronous motor

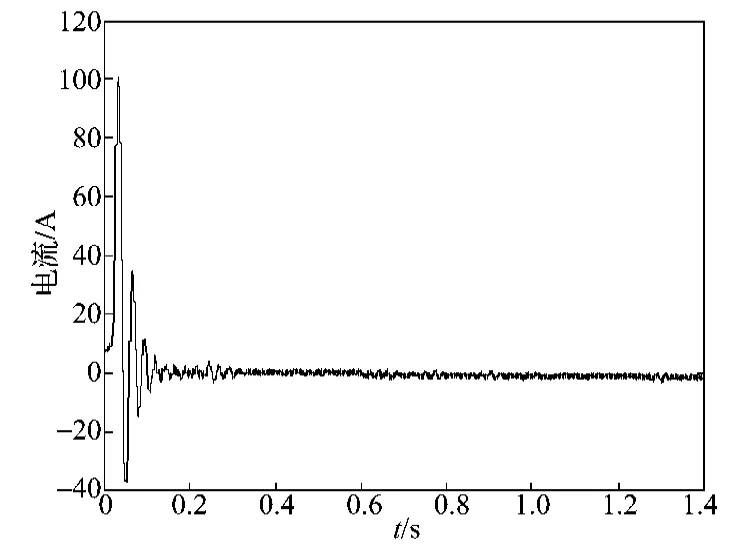
图7 机侧d轴电流Fig.7The d axis current of motor side

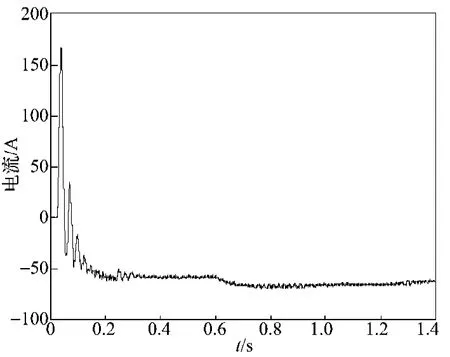
图8 机侧q轴电流Fig.8The q axis current of motor side

由图5～8可以看出，当风速在0.6s由7.0m·s-1变化为7.5m·s-1时，机侧d轴电流始终保持为零，q轴电流随着风速的变化而改变；叶尖速比在风速变化过程中迅速稳定在最大处。当风速变化时，风力发电机组能够一直在稳定的状态下实现风能的最大捕获。以上仿真波形说明本方法达到了所要求的控制目标，证明了此控制算法的正确性[8-9]。

5 结语

本文对风力发电机的工作原理及风力机捕获最大风能的原理进行研究，提出利用叶尖速比控制方法来实现直驱永磁风力发电机的最大风能跟踪。先给出了风力机的数学模型，再根据数学模型建立系统仿真模型，并对永磁同步风力发电机机侧进行了仿真分析。仿真结果表明，风力机在风速发生变化的情况下，能实现最大功率的输出，实现风能的最大捕获。

[1]张课.基于叶尖速比控制的风力发电的最大风能捕获分析[J]. 科技信息，2012(2)：10. Zhang Ke. Maximum Wind Energy Capture Based on Tip Speed Ratio Control[J]. Science & Technology Information，2012(2)：10.

[2]鲁闯，朱东柏，沈中元，等. 直驱风力发电系统MPPT控制方法的研究[J]. 电测与仪表，2008，45(8)：61-64. Lu Chuang，Zhu Dongbai，Shen Zhongyuan，et al. Research on Control Method of Direct-Drive Wind Power Generation System[J]. Elecerical Measurement ＆Instrumentation，2008，45(8)：61-64.

[3]张武.风力发电系统中一种最佳叶尖速比控制策略的研究[D]. 沈阳：沈阳工业大学，2009. Zhang Wu. Research on Optimal Tip-Speed Ratio Control Strategy in Wing Generation System[D]. Shengyang：Shengyang University of Technology，2009.

[4]吴政球，干磊，曾议，等. 风力发电最大风能追踪综述[J]. 电力系统及其自动化学报，2009，21(4)：88-93. Wu Zhengqiu，Gan Lei，Zeng Yi，et al. Summary of Tracking the Largest Wind Energy for Wind Power Generation[J]. Proceedings of the CSU-EPSA，2009，21 (4)：88-93.

[5]尹玲玲，胡育文. 交流电机变速恒频风力发电技术[J]. 电气传动，2005，35(10)：7-10. Yin Lingling，Hu Yuwen. Technology of Variable-Speed Constant Frequency Wind Generating Used AC Machine [J]. Electric Drive，2005，35(10)：7-10.

[6]曹明锋.直驱型永磁同步风力发电系统变流器的控制研究[D]. 株洲：湖南工业大学，2013. Cao Mingfeng. Research on Control of Converter for Direct-Driven Permanent Magnet Synchronous Wind Generation System[D]. Zhuzhou：Hunan University of Thchnology，2013.

[7]杨智，朱海锋，黄以华. PID控制器设计与参数整定方法综述[J]. 化工自动化及仪表，2005，32(5)：1-7. Yang Zhi，Zhu Haifeng，Huang Yihua. Recent Studies of PID Design and Parameter Tuning Method[J]. Control and Instruments in Chemical Industry，2005，32(5)：1-7.

[8]王波，宋金梅，方蒽，等. 基于最佳叶尖速比的最大风能跟踪在永磁直驱风力发电系统中的实现[J]. 电测与仪表，2009，46(9)：82-86. Wang Bo，Song Jinmei，Fang En，et al. The Implementation of the Largest Wind Energy Tracking Based on the Optimum Tip Speed Ratio in Direct-Drive Permanent Magnet Synchronous Generator System[J]. Electrical Measurement＆ Instrumentation，2009，46(9)：82-86.

[9]邱丽，朱晓青，郭百顺.改进的爬山算法在风电最大功率跟踪中的应用[J]. 湖南工业大学学报，2013，27(4)：57-60. Qiu Li，Zhu Xiaoqing，Guo Baishun. Application of Improved Hill-Climbing Algorithm in Maximum Wind Energy Tracing[J]. Journal of Hunan University of Technology，2013，27(4)：57-60.

[10]王刚毅，肖强晖，朱广辉，等. 永磁直驱风力发电机功率控制的研究[J]. 湖南工业大学学报，2013，27(4)：61-65. Wang Gangyi，Xiao Qianghui，Zhu Guanghui，et al. Power Control of Direct-Driven Permanent Magnet Wind Generators[J]. Journal of Hunan University of Technology，2013，27(4)：61-65.

（责任编辑：邓彬）

Implementation of Maximum Wind Energy Tracking in Direct-Drive Permanent Magnet Wind Power Generation System

Li Yong，Zhu Xiaoqing，Huang Ying
（School of Electrical and Information Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China）

Studied the principle of Baez about maximum wind power tracking theory of permanent magnet synchronous wind generator and put forward the tip speed ratio control method. Introduced the mathematical model of wind turbine and the optimal tip speed ratio control method, constructed the mathematical model of permanent magnet synchronous wind power generator, and simulated and analyzed the model by Matlab/Simulink software. The simulation results showed that the proposed method achieved fast and accurate maximum wind energy tracking.

maximum wind energy tracking principle；permanent magnet synchronous generator；wind energy utilization；tip speed ratio control method

TM315

A

1673-9833(2014)05-0059-05

10.3969/j.issn.1673-9833.2014.05.012

2014-06-15

李勇（1987-），男，山东青岛人，湖南工业大学硕士生，主要研究方向为电力电子技术及系统，E-mail：394488703@qq.com