基于滑移线理论考虑桩端摩擦的桩端阻力计算

黄小龙，王志斌

（湖南科技大学土木工程学院，湖南湘潭411201）

基于滑移线理论考虑桩端摩擦的桩端阻力计算

黄小龙，王志斌

（湖南科技大学土木工程学院，湖南湘潭411201）

针对传统桩端阻力计算未考虑中间主应力以及桩端粗糙程度的缺陷，基于一定的滑移线场假设，建立滑移线场，同时考虑中间主应力和桩端粗糙程度的影响，运用滑移线的基本性质，推导出被动区的积分常数，再由主动区的受力情况推导出该区的积分常数，运用同一滑移线上的积分常数相等的性质，推导出既考虑中间主应力又考虑桩端粗糙程度的桩端阻力计算公式。该公式在桩端完全光滑时，可退化为Prandtl解，并且随着b值和桩端粗糙程度的增大，桩端阻力随之增大，与实际情况相符。推导出的公式能够灵活运用于工程实际情况。

双剪统一强度理论；滑移线；中间主应力；桩端阻力；桩端粗糙程度

0 引言

桩端阻力问题一直是岩土工程界关注的重点。桩端阻力计算的传统方法大多是先假设滑动面， 然后按照静力平衡条件和力学迭加原理来求解，其推导不够严密。滑移线理论，是20世纪初人们对金属塑性变形过程中，光滑试样表面出现“滑移带”现象，经过力学分析而逐步形成的一种图形绘制与数值计算相结合的求解平面塑性流动问题、变形力学问题的理论方法。所谓“滑移线”是一个纯力学概念，它是塑性变形区内，最大剪切应力等于材料屈服切应力的轨迹线。土体在受力进入塑性状态之后，与金属有相似的破坏特征，因此滑移线理论也被用于岩土工程分析。许多学者[1-3]应用滑移线理论对浅基础的极限承载力进行了研究，但未能考虑中间主应力的影响。实践表明，中间主应力对土体屈服和破坏的影响较大。俞茂宏等[4]提出的统一强度理论，考虑了中间主应力的影响，用一个统一的力学模型和统一而简单的数学表达式表述材料的强度性质。文献[5-6]推导了Terzaghi地基极限承载力的双剪统一解。文献[7]推导了应用双剪滑移线理论计算桩端阻力的公式。然而大多数文献[5-9]是基于完全摩擦基底或者完全光滑基底的研究，而实际中许多桩端不是处于这2种极限摩擦状态。

本文基于统一强度理论的平面应变形式，结合经典的桩端滑移线场破坏模式，引入滑移线的基本性质及基本假设，并且根据这种形式在考虑桩端摩擦因素的情况下，探讨桩端阻力的计算方法。

1 双剪统一平面应变滑移线场理论

1.1 双剪统一强度理论

双剪统一强度理论是考虑了材料的拉压异性、抗压同性以及不同中间主应力效应的一种全新的强度理论，其数学表达式为

b为加权参数，它反映中间剪应力及相应作用面上的正应力对材料屈服或破坏的影响，0≤b≤1。

当b取不同的值时，式（1）可变为Mohr-Coulomb强度准则、双剪强度理论、Tresca 屈服准则、Misses屈服准则的线性逼近。双剪统一强度理论可以充分反映中间主应力2对材料屈服或破坏的影响。

1.2 平面应变问题的平衡方程

平面应变问题的平衡微分方程为

ct表示双剪统一强度理论下的粘聚力（也称剪切强度）。

当m=1时，

将式（7）～（9）代入不计材料重度的式（2）中，可得

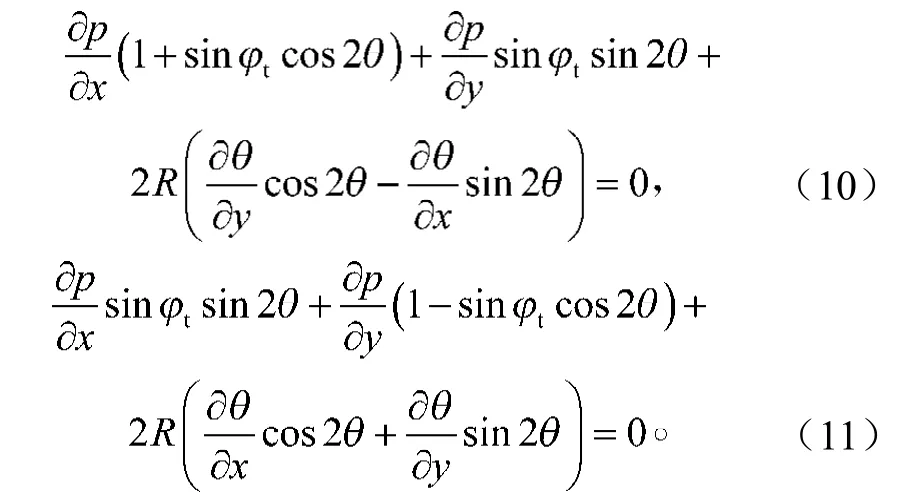
滑移线基本方程为

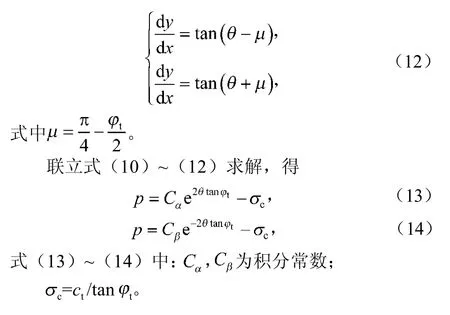
2 边界条件及滑移线的基本性质

2.1 边界条件及屈服准则

图1为塑性边界条件。设边界面的法线与y轴的夹角为，由图1a可知，边界面法线与1的夹角为-。由于塑性区边界面上的应力应满足屈服条件，由图1b可写出平面上法向力与切向力的方程为

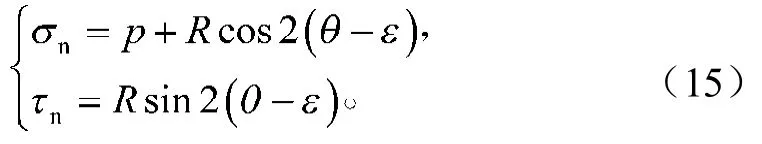
当已知边界上的应力时，可以得到边界上的p和大主应力与y轴的夹角。

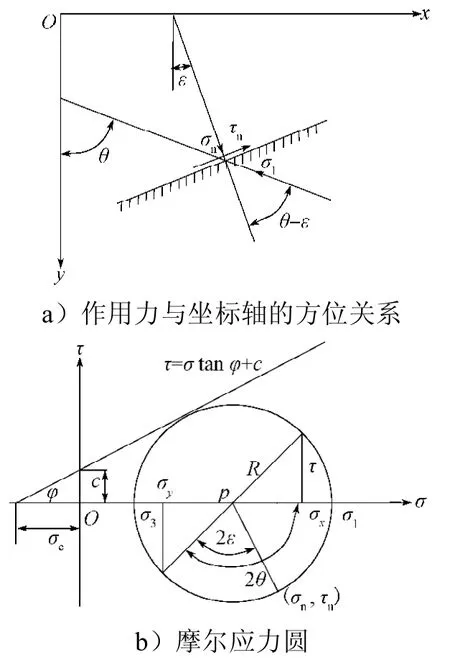
图1 塑性边界条件Fig.1Plastic boundary conditions

2.2 滑移线的基本性质

滑移线的基本性质有：

1）同一条滑移线上的积分常数相等。

2）在某个应力场中，如果为常数，则该应力场为均匀应力场，两族滑移线均为直线。

3）在某个应力场中，如果一族滑移线为直线，另外一族为曲线，则在这一族直线滑移线上的p为常数，不同直线族滑移线上的p不同，这种应力场为简单应力场。

3 计算过程

3.1 基本假设

张学言[1]运用滑移线理论和摩尔库伦屈服准则研究了浅基础的承载力。本文借鉴该方法，对端阻力进行分析。图2为桩端滑移线网，并且对桩端以下土作如下假设：

1）桩端土体是均匀的，各向同性。

2）桩端土满足统一强度理论。

3）通过滑移线网确定桩端破坏区域以及弹塑性状态。对于岩土体材料来说，其拉压强度不等，滑移破坏大都呈明显的非正交特性，即两族滑移线之间的夹角不等于45°。

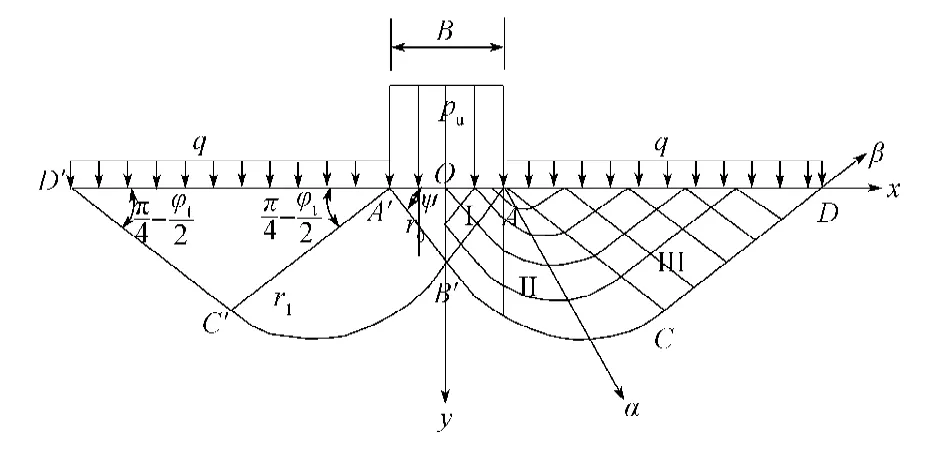
图2 桩端滑移线网Fig.2Pile end slip line network

3.2 计算过程

1）在AD边界上有n=q=h（h为上覆土层厚度），n=0，=0，本区在桩端力的作用下，有向上隆起的趋势，故为被动破坏区。从而得到被动破坏区边界条件为：将这些边界条件代入式（15），得，从而有

联立式（14）与式（16），解得

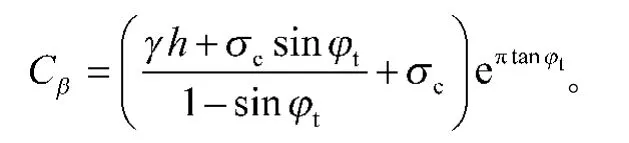
联立式（14）和式 （17），得

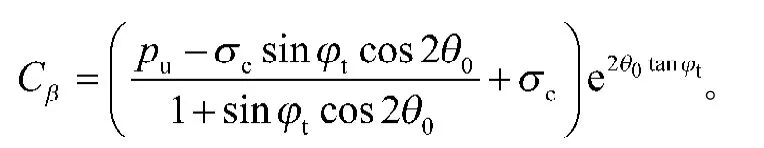
根据滑移线的基本性质1），同一条滑移线上的积分常数相等，有

在桩端不光滑的情况下，桩端土体会由于桩端摩擦而产生一个弹性楔形体，楔形体如图2中的AA′B′。其中楔形体的边界AB′既是一条滑移线，也是弹塑性分界面，它与基底之间的夹角（图2中A′B′与A′A之间的夹角）可以表示为，是大主应力方向与y轴之间的夹角。

由图2中三角形AA′B′的几何关系可得从而可得

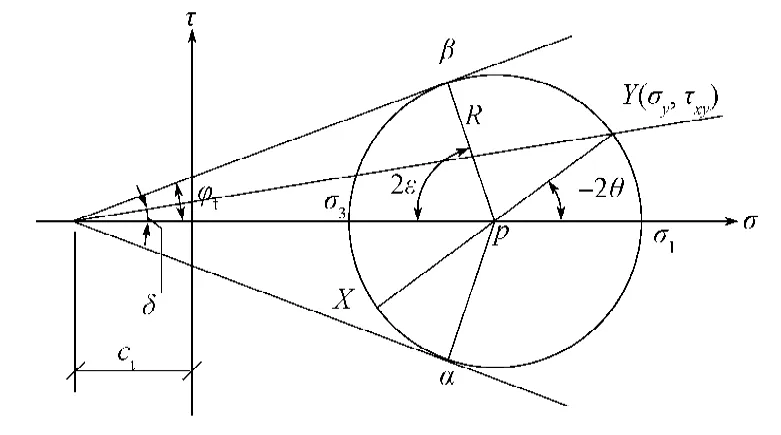
图3 不完全粗糙基底与土体接触面的摩尔圆Fig.3Mohr circle of incomplete rough substrate and soil contact surface

4 算例验证及结果分析

假设有一直径为400mm的圆柱形桩基础，打入均质黏性土6m，黏性土容重为20kN/m3，c0=20kPa，0=30°。在参数b取不同值的情况（即中间主应力取不同值）下，分别运用本文公式（18）以及传统端阻力计算公式求解桩端阻力，计算结果见表1，表1中t和ct由式（5）和式（6）得出。

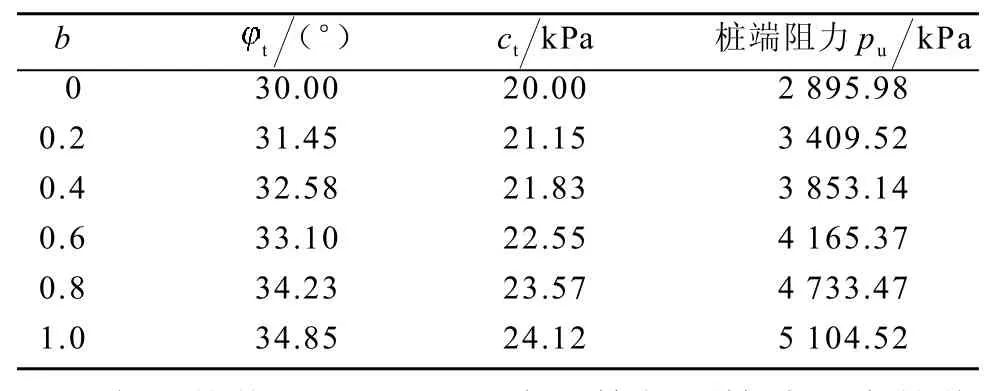
表1 不同b值的桩端阻力计算结果Table1Calculating results of pile end resistance of different values of b

应用传统Terzaghi公式计算得到桩端阻力的值为2808.29kPa。表1中参数b取0（即不考虑中间主应力）时桩端阻力为2895.98kPa，两者结果十分接近，证明了该公式的准确性。由表1可知，当b值增大时，桩端阻力增大，这表明中间主应力对桩端阻力的影响十分明显。

在中间主应力影响因素一定（即b为定值，表2中b均取1）的情况下，通过改变桩端与土体接触面之间的摩擦角来表征基底粗糙程度的变化，由式（18）计算桩端阻力，计算结果见表2，表2中由式（24）得出。

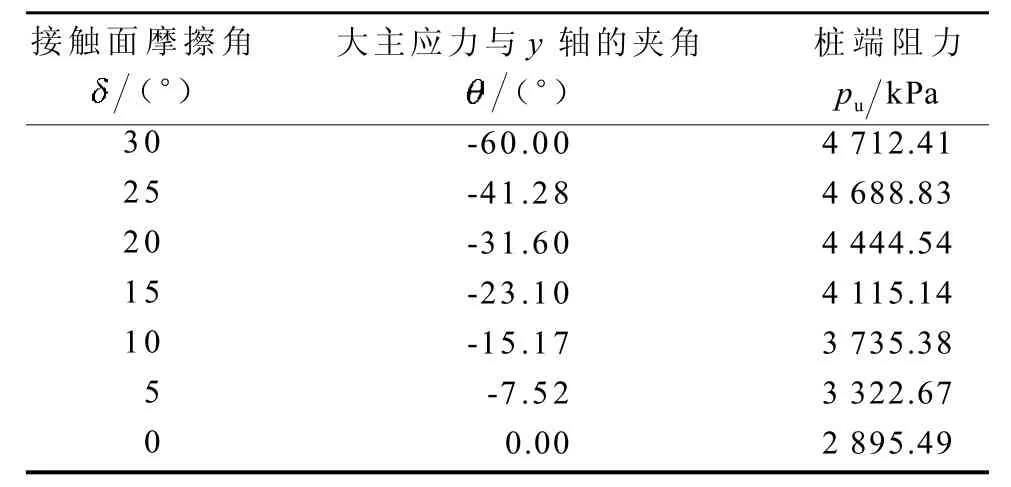
表 2不同粗糙度的桩端阻力计算结果Table2Calculation results of pile end resistance of different roughness

由表2可知，当桩端与土体接触面摩擦角为0时，由式（18）计算桩端阻力为2895.49kPa，而用Prandtl公式计算出的桩端阻力为2794.50kPa，二者结果相近。当增大接触面摩擦角时，表示桩端粗糙程度增大，由式（18）计算的桩端阻力值也增大，表明桩端粗糙程度对桩端阻力的影响明显，并且随着桩端粗糙程度的增大而增大，这与实际情况相吻合。

5 结语

本文基于统一滑移线场理论，给出了不完全摩擦型桩基的桩端阻力计算公式（18），该公式在基底完全光滑时可以退化成Prandtl公式。

采用经典的Terzaghi公式计算得到的桩端阻力比用本文公式（18）计算的结果稍小，说明Terzaghi公式计算结果偏于保守。在考虑中间主应力作用的条件下，桩端阻力随着中间主应力系数的增大而增大，将这一结论运用于工程实践中，可提高经济效益。

不完全摩擦型桩的桩端阻力随着桩端摩擦角的增大而增大，不再局限于完全光滑与完全粗糙两种假设，能够灵活地应用于各种工程实际情况。

[1]张学言. Prandtl和Terzaghi地基承载力的塑性力学滑移线解[J]. 天津大学学报，1987 (2)：92-100. Zhang Xueyan. Prandtl and Terzaghi Bearing Capacity Formulas of a Strip Footing Solved by Slip-Line Method of Plasticity[J]. Journal of Tianjin University，1987 (2)：92-100.

[2]杨江海，黄齐武，李建平. 地基极限承载力的滑移线解法[J]. 西部探矿工程，2007(3)：214-217. Yang Jianghai，Huang Qiwu，Li Jianping. The Method of Characteristics Used in the Bearing Capacity Calculation [J]. West-China Exploration Engineering，2007(3)：214-217.

[3]李丽民，张国祥，肖尚，等. 基于潜在滑移线理论的地基承载力安全分析方法[J]. 中国安全科学学报，2013，23(3)：39-44. Li Limin，Zhang Guoxiang，Xiao Shang，et al. Method for Bearing Capacity Safety Analysis of Foundation Soil Based on Potential Slip Line Theory[J]. China Safety Science Journal，2013，23(3)：39-44.

[4]俞茂宏，杨松岩，刘春阳，等. 统一平面应变滑移线场理论[J]. 土木工程学报，1997，30(2)：14-26. Yu Maohong，Yang Songyan，Liu Chunyang，et al. Unified Plane Strain Slip Line Field Theory System[J]. China Civil Engineering Journal，1997，30(2)：14-26.

[5]范文，白晓宇，俞茂宏. 基于统一强度理论的地基极限承载力公式[J]. 岩土力学，2005，26(10)：1617-1622. Fan Wen，Bai Xiaoyu，Yu Maohong. Formula of Ultimate Bearing Capacity of Shallow Foundation Based on Unified Strength Theory[J]. Rock and Soil Mechanics，2005，26 (10)：1617-1622.

[6]高江平，俞茂宏，李四平. 太沙基地基极限承载力的双剪统一解[J]. 岩石力学与工程学报，2005，24(15)：2736-2740. Gao Jiangping，Yu Maohong，Li Siping. Double-Shear Unified Solution of Terzaghi Ultimate Bearing Capacity of Foundation[J]. Chinese Journal of Rock Mechanics and Engineering，2005，24(15)：2736-2740.

[7]鲁燕儿，郑俊杰，陈保国. 应用双剪滑移线理论计算桩端端阻力[J]. 岩石力学与工程学报，2007，26（增刊2）：4084-4089. Lu Yaner，Zheng Junjie，Chen Baoguo. Determination of End Bearing Capacity of Pile with Double-Shear Slip-Line Theory[J]. Chinese Journal of Rock Mechanics and Engineering，2007，26(S2)：4084-4089.

[8]俞茂宏. 双剪理论及其应用[M]. 北京：科学出版社，1998：35-40. Yu Maohong. Double-Shear Theory and Its Application [M]. Beijing：Science Press，1998：35-40.

[9]周小平，王建华. 考虑中间主应力影响时条形地基极限承载力公式[J]. 上海交通大学学报，2003，37(4)：552-555. Zhou Xiaoping，Wang Jianhua. Influence of Intermediate Principal Stress on the Ultimate Bearing Capacity of Foundation[J]. Journal of Shanghai Jiaotong University，2003，37(4)：552-555.

[10]杨江海. 考虑基底粗糙度的地基极限承载力分析[D]. 上海：同济大学，2007. Yang Jianghai. Study on Bearing Capacity of Foundations with Different Roughness[D]. Shanghai：Tongji University，2007.

（责任编辑：邓光辉）

The Pile Tip Resistance Calculation Considering Pile Tip Friction Based on the Slip Line Theory

Huang Xiaolong，Wang Zhibin
（School of Civil Engineering, Hunan University of Science and Technology, Xiangtan Hunan 411201，China）

For the defects of traditional pile tip resistance calculation without considering the intermediate principal stress and the roughness of the pile end, based on the assumption of slip line field, established the slip line field, and considering the intermediate principal stress and the tip roughness, applied the basic properties of slip line to deduce the integral constant of passive area, then deduced the active area integral constant by the active area force, and by means of the properties of the integral constant equal on the same slip line, deduced pile tip resistance calculation formula considering the intermediate principal stress and pile tip roughness. The formula can degenerate into prandtl solution when pile end is completely smooth, and with the increase of b value and pile end roughness, the pile end resistance increases, which is consistent with actual situation. The formulas can be applied to the engineering practice.

double shear unified strength theory；slip line；intermediate principal stress；pile tip resistance；pile tip roughness

TU473.1+1

A

1673-9833(2014)05-0027-05

10.3969/j.issn.1673-9833.2014.05.006

2014-07-28

黄小龙（1990-），男，湖南湘潭人，湖南科技大学硕士生，主要研究方向为岩土与地下工程，E-mail：283854103@qq.com