改进的模糊C-均值算法在图像分割中的应用

周丹，肖满生，刘丽红，姚慧丹

（湖南工业大学计算机与通信学院，湖南株洲412007）

改进的模糊C-均值算法在图像分割中的应用

周丹，肖满生，刘丽红，姚慧丹

（湖南工业大学计算机与通信学院，湖南株洲412007）

针对传统的模糊C-均值算法在图像分割中存在的缺陷，提出了一种基于点密度函数加权的模糊C-均值聚类算法。将图像像素的点密度函数作为权值，并依据类间相关度定义了一个聚类有效性函数用以确定最佳聚类数，结合聚类有效性完成对图像的分割。理论分析和对比试验表明，该算法在一定程度上克服了模糊均值算法的缺陷，在图像分割中具有良好的分类精度。

模糊C-均值；点密度函数；聚类有效性；图像分割

0 引言

在对图像的研究和应用中，往往需要从复杂的图像背景中将感兴趣的目标分割出来，这些部分一般对应于图像中具有独特性质的区域，如像素的灰度值、物体轮廓曲线、纹理等。图像分割的好坏直接影响计算机视觉对图像的理解[1]，图像分割[2-4]的方法已有上千种，典型的分割方法大致可分为基于阈值的方法、基于区域生长和基于边缘检测的方法等。由于视觉对色差的模糊性，模糊聚类分析受到了人们普遍的关注，模糊C-均值聚类[5]（fuzzy C-means，FCM）是当今最流行的模糊聚类算法之一。它把聚类归结成一个带约束的非线性规划问题，通过优化求解获得数据集的模糊划分和聚类，但该算法只考虑了图像中的数值特征信息，而忽略了样本矢量间对聚类结果的影响。在实际的图像处理过程中，由于噪声等因素的干扰及最小化误差平方和目标函数具有对数据集进行等划分的趋势，目前已有学者通过对传统的FCM算法进行加权改进如二维直方图加权，特征加权等改进方法。考虑到数据集在现实生活中的实际分布特征，基于数据的分布对分类的不同影响程度，本文提出了一种新的样本加权的FCM算法，借助像素样本本身的分布特性，利用其点密度函数[6-8]作为权值对传统算法进行改进，使聚类中心进行调整，从而克服了传统FCM算法对样本集进行等划分的缺陷，降低了图像分割的错分率，提高了图像分割的精度。

1 模糊C-均值聚类算法

随着对模糊聚类算法研究的深入发展，该算法已经有效地应用于大规模数据分析、图像分割与识别、数据挖掘等领域，模糊C-均值聚类算法是模糊聚类的基本方法之一。它是一种对数据样本进行自动分类的方法，通过优化目标函数得到每个样本点对类中心的隶属度，进而决定每个样本点归属于哪一类。这种无监督的分类方法被有效地应用于图像自动分割问题上。

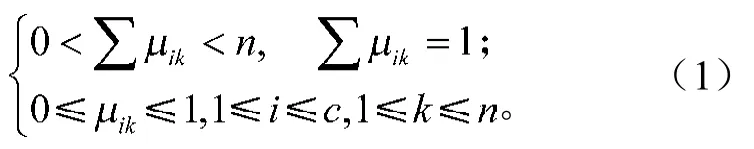
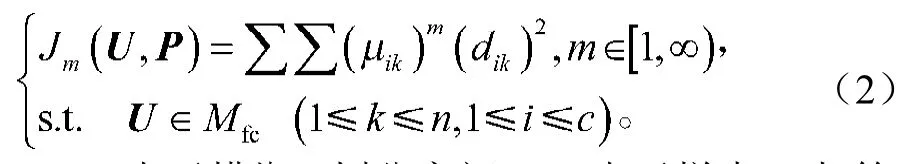
式中：Mfc表示模糊c划分空间；dik表示样本xk与第i类的聚类原型pi之间的欧式距离量度。其中dik用式（3）计算，即

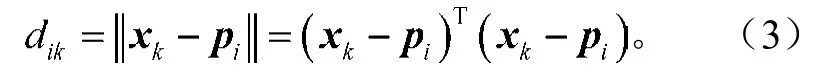
FCM聚类过程如下。

初始化：给定聚类类别数c，数据的个数为n，其中2≤c≤n，加权系数，设定迭代停止阈值，迭代计数器b=0，初始化聚类原型模式p(0)。第一步：用以下规则更新划分矩阵U(b)。

第二步：用式（4）更新聚类原型矩阵p(b+1)，即

2 加权模糊C-均值算法与聚类有效性评定

J. C. Bezdek指出，传统的FCM聚类算法在实现过程中，由于最小化误差平方和目标函数对数据集具有等划分趋势这一缺陷的存在，针对该问题提出了一种加权的FCM算法。利用点密度函数作为加权系数，一方面充分利用了数据集的本身分布特性，另一方面点密度函数反映样本点的聚集情况，作为加权系数能更贴近样本点的实际分布情况，在一定程度上克服了数据集等划分趋势，提高了图像的分割精度。

2.1 基于点密度函数的加权系数计算

对于一个数据集来说，不能十分确切地给出每个样本的典型程度，即某一对象不是确定属于某一类，而是在某种程度上属于某一类。考虑到数据集存在一个分布密度问题，将每个数据点的影响用一个数学函数来形式化地模拟，它描述一个数据点在该区域的影响，被称为影响函数[10]。当样本点周围的其它样本点密集程度越高，该样本点的影响函数值越大，对分类影响越大；反之，样本点周围的其它样本点密集程度越低，该样本点的影响函数值越小，对分类影响越小。基于以上原因，本文提出了一种点密度函数作为加权系数的计算方法。对每个样本点xk周围的点密度函数定义为

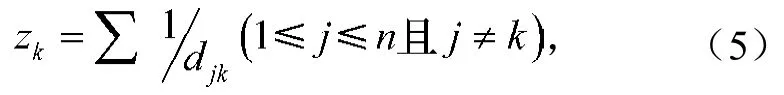
对k进行归一化可得

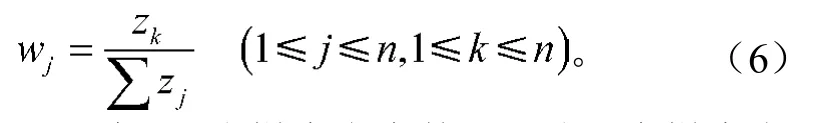
式（5）～（6）中：n为样本点个数；djk为2个样本点xk和xj之间的欧氏距离且djk≤e，e为点密度的范围限定值；wj为样本xj对分类的影响程度。由定义式可以看出样本点周围的点越多则k的值越大。

2.2 加权模糊C-均值聚类算法

根据上面的分析，加权模糊C-均值（weighted fuzzy C-means，WFCM）聚类算法目标函数定义为

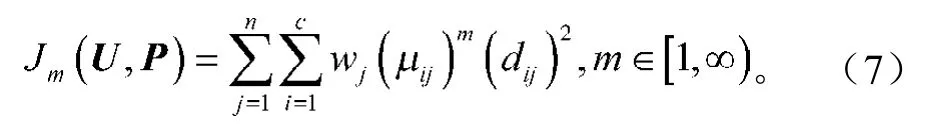
加权系数wj的主要作用在于调整聚类中心，当时即认为各样本对分类的影响是一致的，此时WFCM算法就退化为经典的FCM算法了。利用拉格朗日乘数法求得式（7）的优化迭代公式：

2.3 聚类有效性函数

对于数据集的模糊划分，模糊偏差反映了一个类的样本点的分布情况。基于此，与聚类有效性[11-12]相关的概念定义如下。

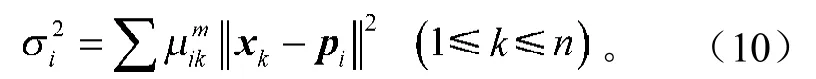
模糊相关度：第i类模糊子集Xi和第j类模糊子集Xj的模糊相关度定义为

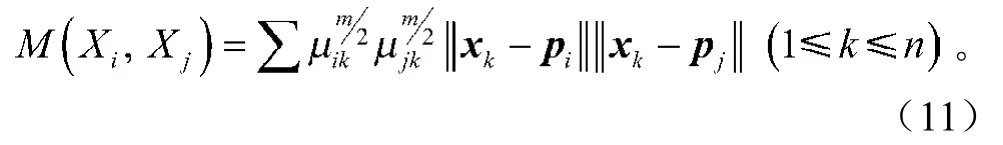
聚类有效性函数：对于一个好的分类而言，类与类间的模糊相关度应尽量小。本文基于类间相关度，定义了一个聚类有效性函数

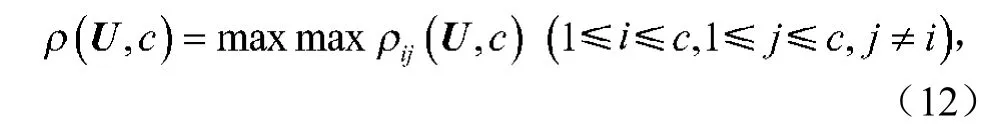
2.4 WFCM算法与聚类有效性评定的实现步骤

WFCM算法与聚类有效性评定的步骤如下：1）初始化，加权指数m=2（经验值），聚类数c用for循环实现从2到6的取值；

2）设定迭代停止阈值，迭代计数器b=0，初始化聚类原型模式p(0)；通过改进的式（8）～（9）进行迭代更新并计算目标函数Jm(U, P)的值；

5）取c*作为聚类数，比较传统的FCM算法与加权的WFCM算法对图像分割的有效性。

3 试验结果与分析

本试验使用MatlabR2012a，在Pentium3G和4G内存的微机上进行。为了验证算法的有效性，分别采用一幅像素的人脑磁共振图像和标准的Lena灰度图像为例进行仿真试验。加权指数m的取值，由于缺乏理论依据的指导，按照聚类有效性研究的结果，N. R. Pal和J. C. Bezdek提出模糊加权指数的取值区间为[1.5, 2.5]时FCM聚类算法的结果最优。本文取m=2进行试验，迭代次数缺省值设为100，迭代终止阈值为0.01。在Matlab试验平台下，对图像最佳聚类数的确定过程如图1所示。

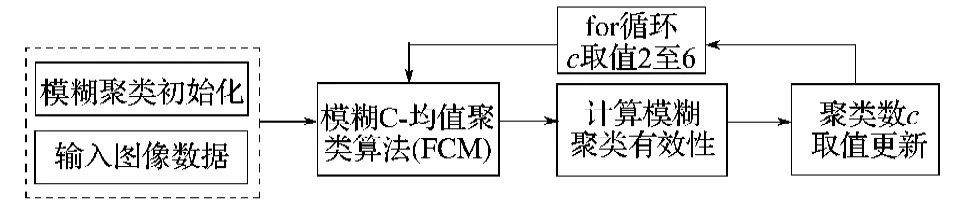
图1 确定最佳聚类数过程图Fig.1The process diagram for determining the optimal number of clusters

在聚类之前分别给定不同的聚类数并初始化聚类中心，利用传统的FCM算法，计算聚类有效性函数(U, c)的值，得到表1所示的结果。

表1 不同聚类数时聚类有效性(U, c)的值Table1The effective cluster value(U, c) for different cluster numbers

表1 不同聚类数时聚类有效性(U, c)的值Table1The effective cluster value(U, c) for different cluster numbers

c (U, c) 23456 0.83210.82970.72540.82680.8432

由表1的试验数据可知，最佳聚类数为4，当c取4时，聚类有效性(U, c)的取值最小。对人脑MR图像进行试验，图像主要包括脑白质、脑灰质、脑脊髓和背景4个部分，所以最佳聚类数为c值取4，与试验预期结果相符。

试验在同等的运行环境下，借助于Matlab图像处理工具进行编程实现，分别用传统的FCM算法和本文改进的方法对同一幅图像进行分割试验，结果如图2所示。

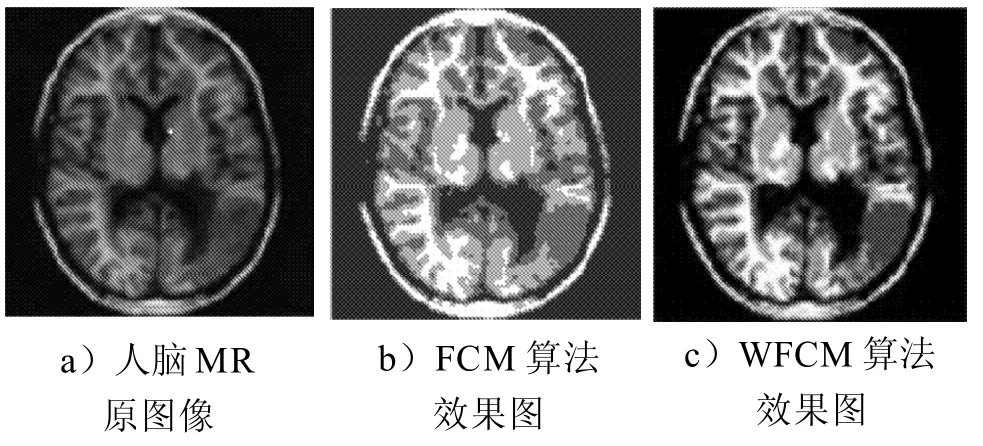
图2 改进算法与原算法的对比Fig.2Comparison of the improved algorithm and the original algorithm

从图2的分割效果图比较结果可以看出传统的FCM算法仅根据当前的像素对图像进行分割，忽略了周围像素点的影响，分割的效果并不好。本文改进的算法显示出良好的抗噪能力并考虑了周围像素点对样本点的影响程度，得到了很好的分割效果。2种算法处理图像过程中的迭代次数和错分率的比较，如表2所示。

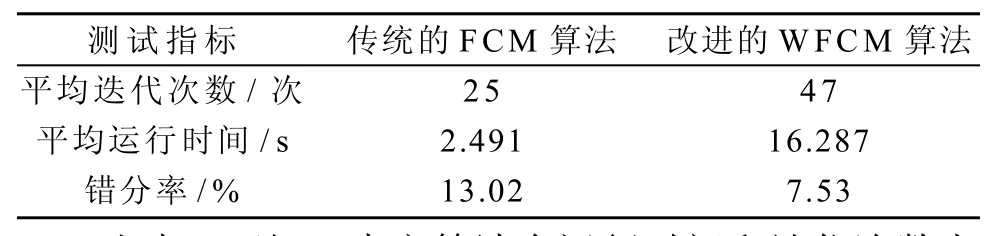
表2 不同的算法对图像进行分割Table2Different algorithms for image segmentation

由表2可知，本文算法在运行时间和迭代次数上比传统的FCM算法高，但在分割过程中的错分率却大大降低，WFCM算法因为在特征空间上进行加权运算，比传统的算法更为复杂，因此在迭代次数和运行时间上会耗时较多，但却能保证精确度并达到较好的分割效果。

采用Lena图像进行对比试验，图像尺寸为512× 512像素，灰度级为256。算法中参数取2，其他参数条件不变。分别采用传统的FCM算法和点密度加权的WFCM算法对图像进行分割处理，分割结果如图3所示。从图中可以看出，传统的FCM算法不能很好地去除噪声，在很多细节方面如人物的鼻梁、嘴角、肩膀、所戴的帽子等都含有噪声，分割结果中还存在一些误分现象，导致有些边界模糊不清，而WFCM算法能够很好地克服这一缺点，并在一定程度上降低错分率，从而较好地分割出目标。

图3 改进算法对Lena图像的分割Fig.3The improved algorithm for Lena image segmentation

4 结语

利用传统的FCM算法非监督模糊聚类的特点对图像进行分割减少人为的干预。为了弥补传统的模糊C-均值算法在图像分割中存在的缺陷，提出聚类相关度的定义作为聚类有效性函数先确定最佳聚类数的取值，然后考虑到周围像素点对样本点的影响程度提出点密度函数作为加权系数对算法进行改进，使图像的分割更为准确。

[1]张德丰. MATLAB数字图像处理[M]. 第二版. 北京：机械工业出版社，2012：268-295. Zhang Defeng. MATLAB Digital Image Processing[M]. 2nd ed. Beijing：China Machine Press，2012：268-295.

[2]何俊，葛红，王玉峰. 图像分割算法研究综述[J]. 计算机工程与科学，2009，31(12)：58-61. He Jun，Ge Hong ，Wang Yufeng. Survey on the Methods of Image Segmentation Research[J]. Computer Engineering and Science，2009，31(12)：58-61.

[3]邵罕. 基于自适应模糊聚类分析的图像分割算法研究[D]. 信阳：信阳师范学院，2012. Shao Han. Study on Image Segmentation Algorithm Based on Auto-Adaption Fuzzy Clustering Analysis[D]. Xin Yang：Xinyang Normal University，2012.

[4]宋寅卯，刘磊. 图像分割研究方法及进展[J]. 电脑学习，2010(2)：1-3. Song Yinmou，Liu Lei. The Methods and Process of Image Segment[J]. Computer Study，2010(2)：1-3.

[5]高新波. 模糊聚类分析及其应用[M]. 西安：西安电子科技大学出版社，2004：49-54. Gao Xinbo. Fuzzy Clustering Analysis and Its Applications [M]. Xi’an：Xi’an University of Electronic Science and Technology Press，2004：49-54.

[6]沈忠阳，覃亚丽. 基于改进模糊均值聚类算法的遥感图像聚类[J]. 杭州电子科技大学学报，2012，32(4)：99-101. Shen Zhongyang，Qin Yali. Remote Sensing Image Clustering Based On Modified FCM Clustering Algorithm [J]. Journal of Hangzhou Dianzi University，2012，32(4)：99-101.

[7]刘小芳，曾黄麟，吕炳朝. 点密度函数加权模糊C-均值算法的聚类分析[J]. 计算机工程与应用，2004，40(24)：64-65. Liu Xiaofang，Zeng Huanglin，L Bingchao. Clustering Analysis of Dot Density Function Weighted Fuzzy CMeans Algorithm[J]. Computer Engineering and Applications，2004，40(24)：64-65.

[8]李金秀，高新波，高玉娥，等. 基于特征加权的模糊聚类算法研究[J]. 北京电子科技学院学报，2007，15(2)：74-76. Li Jinxiu，Gao Xinbo，Gao Yu’e，et al. A Feature Weighted Fuzzy Clustering Algorithm[J]. Journal of Beijing Electronic Science and Technology Institute，2007，15(2)：74-76.

[9]Bezdek J C. Pattern Recognition with Fuzzy Objective Function Algorithms[M]. New York：Plenum Press，1981：637-641.

[10]孟海东，马娜娜，宋宇辰，等. 基于密度函数加权的模糊C均值聚类算法研究[J]. 计算机工程与应用，2012，48 (27)：123-127. Meng Haidong，Ma Na’na，Song Yuchen，et al. Research on Fuzzy C-Means Clustering Algorithm Based on Density Function Weighted[J]. Computer Engineering and Applications，2012，48(27)：123-127.

[11]陈舵，李雪，崔杜武，等. 一种基于模糊度的聚类有效性函数[J]. 模式识别与人工智能，2008，21(1)：34-41. Chen Duo，Li Xue，Cui Duwu，et al. Clustering Validity Function Based on Fuzzy Degree[J]. Pattern Recognition and Artificial Intelligence，2008，21(1)：34-41.

[12]肖满生，阳娣兰，张居武，等. 基于模糊相关度的模糊C均值聚类加权指数研究[J].计算机应用， 2010，30(12)：3388-3390. Xiao Mansheng，Yang Tilan，Zhang Juwu，et al. Research of Weighting Exponent of Fuzzy C-Means Algorithm Based on Fuzzy Relevanc[J]. Journal of Computer Applications，2010，30(12)：3388-3390.

（责任编辑：申剑）

Application of Improved Fuzzy C-Means Algorithm in Image Segmentation

Zhou Dan，Xiao Mansheng，Liu Lihong，Yao Huidan
（School of Computer and Communication，Hunan University of Technology，Zhuzhou Hunan 412007，China）

For the defects of traditional fuzzy C-means algorithm in image segmentation, a weighted fuzzy C-means clustering algorithm based on dot density function are proposed. Takes the dot density function of image pixels as the weight, and on the basis of inter-class correlation defines a cluster validity function to determine the optimal number of clusters and combines with cluster validity to complete the effective image segmentation. Theoretical analysis and comparative experiments show that the algorithm overcomes the shortcomings of fuzzy means algorithm to some extent and has good classification accuracy in image segmentation.

fuzzy C-means；dot density function；cluster validity；image segmentation

TP391

A

1673-9833(2014)05-0079-05

10.3969/j.issn.1673-9833.2014.05.016

2014-03-13

国家自然科学基金资助项目（61170102），湖南省教育厅重点基金资助项目（12A042）

周丹（1989-），女，湖南工业大学硕士生，主要研究方向为智能图像处理，E-mail：787868810@qq.com