卡尔曼滤波在阳山金矿控制测量中的应用

叶 培

（武警黄金第十二支队，成都 610036）

武警黄金十二支队对甘肃文县阳山金矿带进行了大面积GPS控制测量，由于阳山地区地形、气候复杂，切割和高差较大，如果利用传统方法不能保证在有效星历的情况下采用最优信号源，星历残差也较为复杂，特别是信号波源不能稳定在一个有效的区间内。因此，利用卡尔曼滤波数学模型对控制测量中的GPS信号、星历和残差进行优化，从而在同一时、间同一地点、同一天气的情况下尽量提高GPS精度。

1 卡尔曼滤波

1960年，卡尔曼发表了用递归方法解决离散数据线性滤波问题的论文。在这篇文章里，一种克服了维纳滤波缺点的新方法被提出来，这就是我们今天称之为卡尔曼滤波的方法。卡尔曼滤波应用广泛且功能强大，它可以估计信号的过去和当前状态，甚至能估计将来的状态，即使并不知道模型的确切性质[1]。

1.1 滤波器的计算模型

从建立的系统数学模型出发，可以导出卡尔曼滤波的计算原型，包括：时间更新方程和测量更新方程。为了便于描述，做以下说明：⑴X Rnk⊂ ，第K步之前的状态已知的情况下第K步的先验状态估计值；⑵ Xk⊂Rn，测量Zk已知情况下第K步的后验状态估计值。由此定义先验估计误差和后验估计误差：

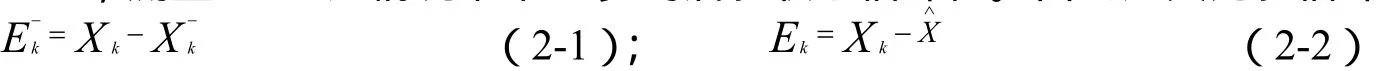
先验估计误差的协方差矩阵为：

后验估计误差的协方差矩阵为：

先验代表的是对过去波形的描述，后验是对未来波形的预测，而测量的过程中，信号总是有残差的存在的，残差采取迭代的数学方法进行转换，将Pk对K进行求导，使一阶导数为零，我们可以得到残差的数学形式[2]：

1.2 滤波器模型的建立

卡尔曼滤波器包括两个主要过程：预估与校正。预计过程主要是利用时间更新方程建立对当前状态变量和误差协方差估计的值，以便在下一个时间状态构造先验估计值；校正过程负责反馈，利用测量更新方程在预测过程的先验估计值及当前测量变量的基础上建立起对当前状态的改进的后验估计。这样一个过程，我们称之为预估-校正过程，对应的方法我们可以称为预估-校正法。

时间更新方程：

状态更新方程：

2 阳山金矿控制测量卡尔曼滤波模型的建立

2012年中国黄金公司要求对阳山金矿带安坝矿段七个控制点进行复测，得到数据要求与2001年所测数据误差必须在规范以内。当时的困难很多，首先时间紧，没有充分的时间进行星历预测，并且施工期间，雨水多，云层厚，天气情况极为恶劣，最关键的问题，两次测量相隔时间近11年，误差除08年地震造成测量标志移动因素外，还有不同时间段的气候、信号和电离层都有可能对数据造成影响，为了取得最优的信号，尽量避开信号干扰，我们决定采用卡尔曼滤波数学模型，对GPS信号、星历和残差进行优化，从而满足工程需要。

2.1 系统状态方程的建立

首先考虑局部卡尔曼滤波器1，这种标准的滤波器模型为：

再考虑局部卡尔曼滤波器2，这种标准的滤波器模型为：

2.2 选用卡尔曼滤波器算法

在上述方程的建立中，考虑到机动速度均值和方差的自适应算法，分别对应于GPS定位系统（3-1）和（3-2）两个模型。在联合卡尔曼滤波器中，对应于各局部滤波器和主滤波器的信息分配系数β1、β2、…βm的取值决定了联合卡尔曼滤波器的信息分配系数的性能。就前面所设计的GPS组合导航系统的联合卡尔曼滤波器的性能，因此可通过选择不同的信息分配系数来改变滤波器的性能，以满足不同的需要。根据信息分配原理，有：

此次工作的性质决定了，我们面对的是一种极端情况，即令β1为0，β2为1，对滤波器1有：因为β1为0，故经推导可知，此时模型1输出的状态估计值对整体状态的影响最小。在实际算法中，不可能出现β1为0，β2为1，否则将会出现发散，但可根据需要取β1或β2为尽可能最小的值。经过大量的计算和平差，我们可以发现β1和β2都为0.5时，联合卡尔曼滤波器输出的值最佳。若β1＞0.5、β2＜0.5，则滤波器的整体输出性能上以局部滤波器模型1为主，且β1越接近于1，而β2越接近于0，滤波器的整体输出中模型1所占的比例会越大，即整个滤波器性能上越接近于模型1，这也是我们在实地计算中所希望的。

若能根据具体情况自动调整β1和β2的大小，这时联合卡尔曼滤波器便成为一种自适应联合卡尔曼滤波器。利用 GPS接收机输出的反映定位精度的参数为依据，自动调整β1和β2的大小。本文使用的是天宝4600LS接收机，其定位精度完全有p反应（包括卫星测量误差），可根据p大小，来决定β1和β2的取值。β1和β2的自适应算法为[3]：

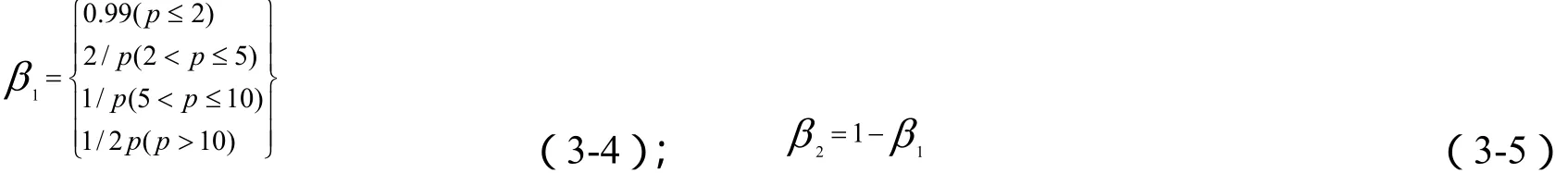
3 结果分析、演算和比较

当选用了适当的数学模型、状态和滤波器后，我们来看看在实际工作中各个过程的分析、演算和比较。整个平差过程采用天宝公司的软件TBC1.0进行计算。我们可以先来看看如果没有选用卡尔曼滤波，卫星残差和卫星星历的稳定情况（图1）。

从图1可以看到，2012年5月7日平差软件自动采取了星历最优的10颗卫星，其中可以看到G3、G19、G20、G32的卫星星历信号非常不稳定，残差较大，基本不能使用，信号较好的只有 G13、G16、G23、G30和G31，G6前一个时段的信号也并不稳定。

图1 未使用卡尔曼滤波卫星星历图

图2 未使用卡尔曼滤波卫星信号残差图

图3 使用卡尔曼滤波卫星星历图

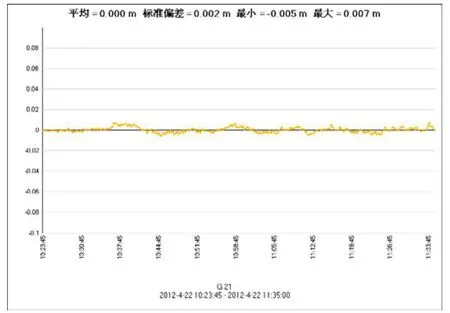
图4 使用卡尔曼滤波卫星信号残差图

图2是卫星信号残差图的显示，从图的显示来看，标准偏差软件默认为0.006M，但是这里最大和最小的误差都达到了0.013M，从理论上来讲，已经超限，并且，从10点23分45秒到11点28分45秒，卫星信号为零，信号从11点28分45秒之后出现，波动也较大，这样的信号和残差取得数据精度基本是不可靠的。

表1是矢量表，表2是标准误差表，表4-3是后验协方差矩阵，从上面三个表格看出，没有使用卡尔曼滤波，得到的GPS平差的几个重要数据，也符合规范要求，但平差情况不是最优。

表1 未使用卡尔曼滤波矢量表

表2 未使用卡尔曼滤波标准误差表

接下来，我们再看看，当我们使用了卡尔曼滤波模型之后出现的信号源和残差情况。

图 3是采用了卡尔曼滤波后的卫星信号残差图的显示，从图的显示来看，标准偏差软件默认为0.002M，但是这里最小误差为-0.005M，最大误差也仅为0.007M，从理论上来讲，平差结果不仅符合规范，精度也达到最佳。GPS整个观测从10点23分45秒到11点33分45秒卫星信号非常稳定，波动较小，误差始终围绕标准误差均匀波动。表4-3、表4-4和表4-5分别是使用卡尔曼滤波模型后的矢量表，标准误差和后验协方差矩阵。从以上三个表格看出，使用卡尔曼滤波，得到的GPS平差的几个重要数据，不仅符合规范要求，平差情况也达到最优。

表3 未使用卡尔曼滤波后验协方差矩阵表

表4 使用卡尔曼滤波矢量表

表5 使用卡尔曼滤波标准误差表

金控制测量以金子山和马齿梁为已知控制点，通过测量平差后得到的未知坐标结果见表7，几个未知坐标的增量变化见表8。

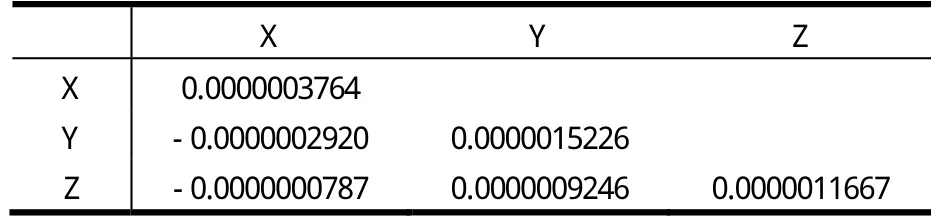
表6 使用卡尔曼滤波后验协方差矩阵表

4 结论

从以上图和表格的数据比较和分析，我们不难可以得出以下结论：卡尔曼滤波数学模型可以大大提高GPS控制测量精度，可以大大减弱卫星信号残差、使星历信号尽量保持在一个较小区间内波动，从而优化平差演算过程。

表7 平差测量所得未知坐标

表8 未知坐标增量变化表

[1] 彭丁聪. 卡尔曼滤波的基本原理及应用. 软件导刊，2009.

[2] 敬喜. 卡尔曼滤波器及其应用基础[M]. 北京：国防工业出版社，1973.

[3] 于德兴，杨兆升，刘雪杰. 基于卡尔曼滤波的GPS/DR导航信息融合方法[Z]. 2006.