重力高阶导数的正演研究

陈永凌，蒋首进，谢丹

（1.武警黄金十二支队，成都 610059；2.武警黄金十支队，昆明 650000 )

1 问题的提出

重力勘探，是所有物探方法中，发展最早、广泛应用的方法之一。它以天然重力场为研究和观测的对象，是建立在地壳中不同岩、矿石间的密度差的基础上，通过观察与研究天然重力场的变化规律来查明地质构造和寻找矿产的一种物探方法。重力勘探经过长期的发展，与其他物探方法相比较，已经成为了一个相对成熟、有独立的理论体系和处理方法的系统。主要研究地壳深部构造；区域地质构造划分；查明区域构造，确定基底起伏发现盐丘背斜等局部构造；普查与勘探金属矿床，查明与成矿有关的构造和岩体。

但是探测目的体产生的重力异常相对整个重力场是很微小的，因此重力弱信号的提取和异常分离是重力数据处理的重中之重，也是重力异常解释的必要前提。 重力异常的复杂性，决定了重力数据处理方法的多样性。常规导数方法主要包括水平导数法和垂向导数法。重力异常的导数在不同形状地质体上有不同的特征，有助于对异常的解释和分类；可以突出浅而小的地质体的异常特征而压制区域性深部地质因素的影响，亦可以将几个相互靠近、埋深相差不大的相邻地质因素引起的叠加异常划分开来，且导数的次数越高，这种分辨能力就越强。

2 模型的确定

针对地下的复杂形体，因为目的体在形状、构造和剩余密度上的差别，如何选择一个正确的模型来模拟计算，会对目的体的形状和空间位置的确定和我们工作的效率产生很大的影响。本文主要探讨模型为圆柱体的二维剖面异常的变化特征。

2.1 圆柱体模型

2.1.1 半径、埋深均相等的圆柱体

模型为沿X向依次排列、截面圆心距相同均为500m、多个中心埋深相等均为300m、半径相等均为180m的均匀圆柱体，剩余密度均为2.67g/cm3。模型的重力异常、水平一阶导数、垂向一阶数和垂向二阶导数的剖面曲线图分别如图1～4。

2.1.2 半径不等、埋深相等的圆柱体

模型为沿X向依次排列的多个中心埋深相等均为300m、截面圆心距相同均为500m、半径不相等的均匀圆柱体。模型中间的圆柱体半径相等均为180m，两边的圆柱体半径100m，剩余密度均为2.67g/cm3。模型的重力异常、水平一阶导数、垂向一阶导数和垂向二阶导数的剖面曲线图分别如图5～8。

2.1.3 半径不等、埋深相等的圆柱体

模型为沿X向依次排列的多个中心埋深相等均为300m，半径不相等的均匀圆柱体，它们分布。其圆心距相同均为500m，半径小的圆柱体截面半径均为100m，半径大的圆柱体截面半径为180m，剩余密度均为错误！未找到引用源。。模型的重力异常、水平一阶导数、垂向一阶导数和垂向二阶导数的剖面曲线图分别如9～12。

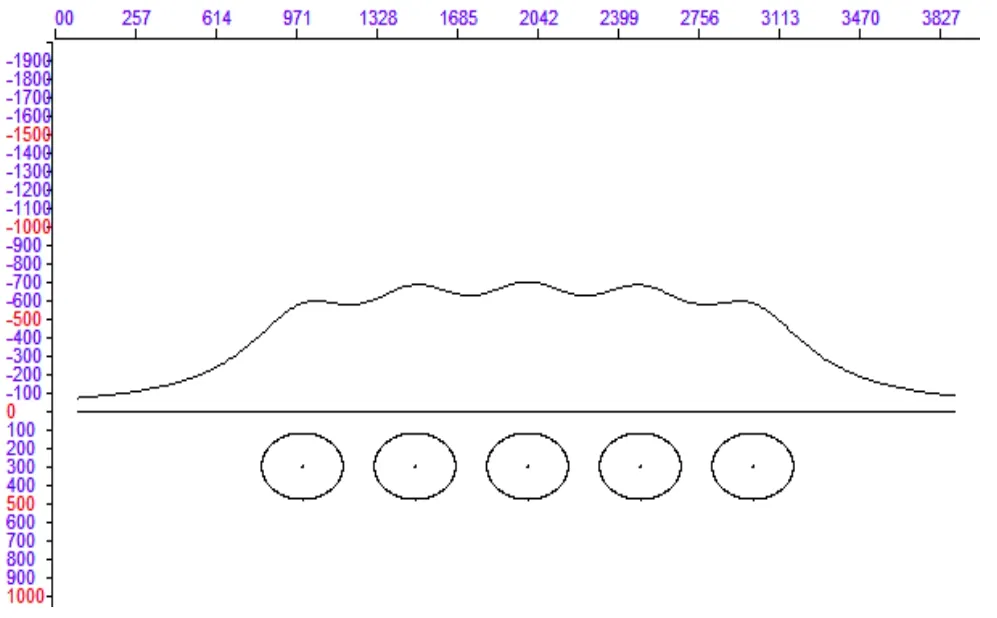
图1 模型重力异常曲线图

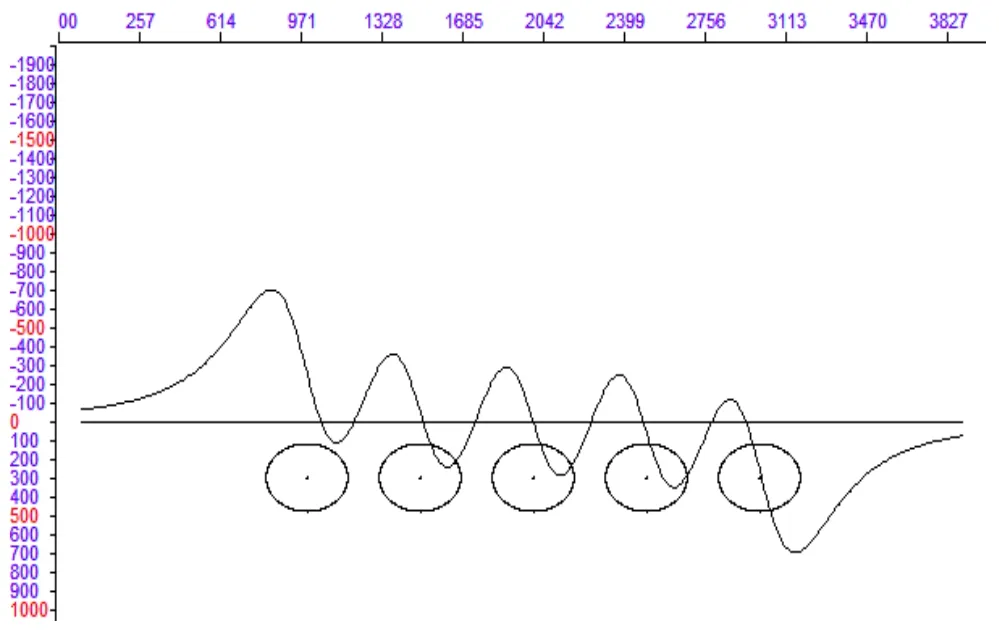
图2 模型重力异常水平一阶导数曲线图

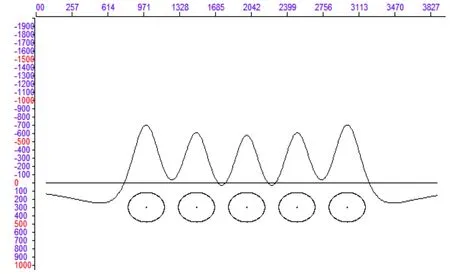
图3 模型重力异常垂向一阶导数曲线图

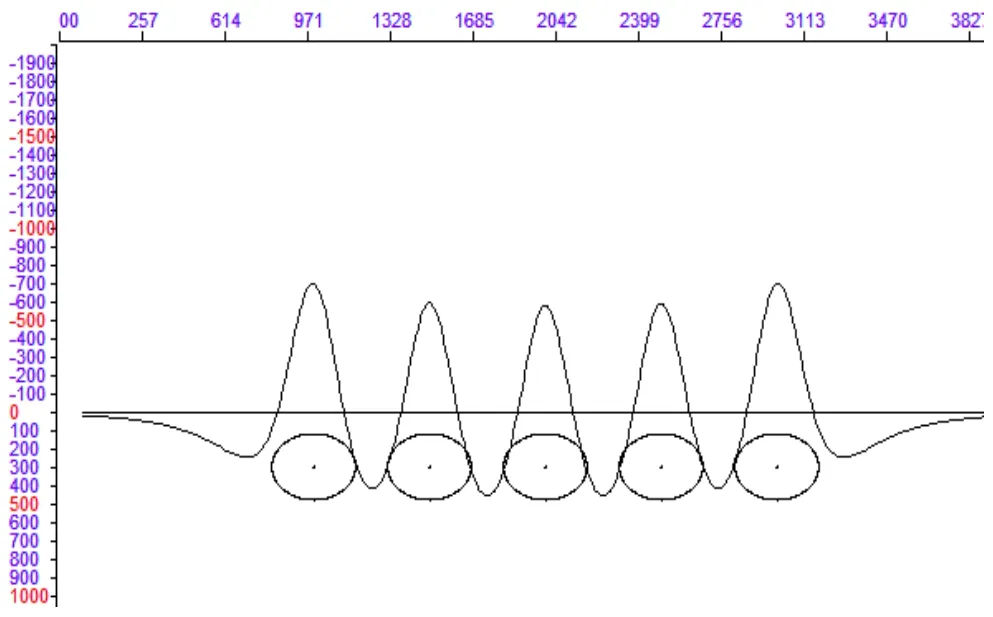
图4 模型重力异常二阶导数曲线图

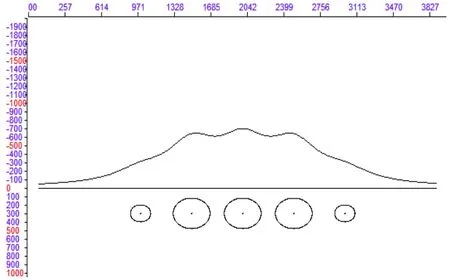
图5 模型重力异常曲线图

图6 模型重力异常水平一阶导数曲线图

图7 模型重力异常垂向一阶导数曲线图

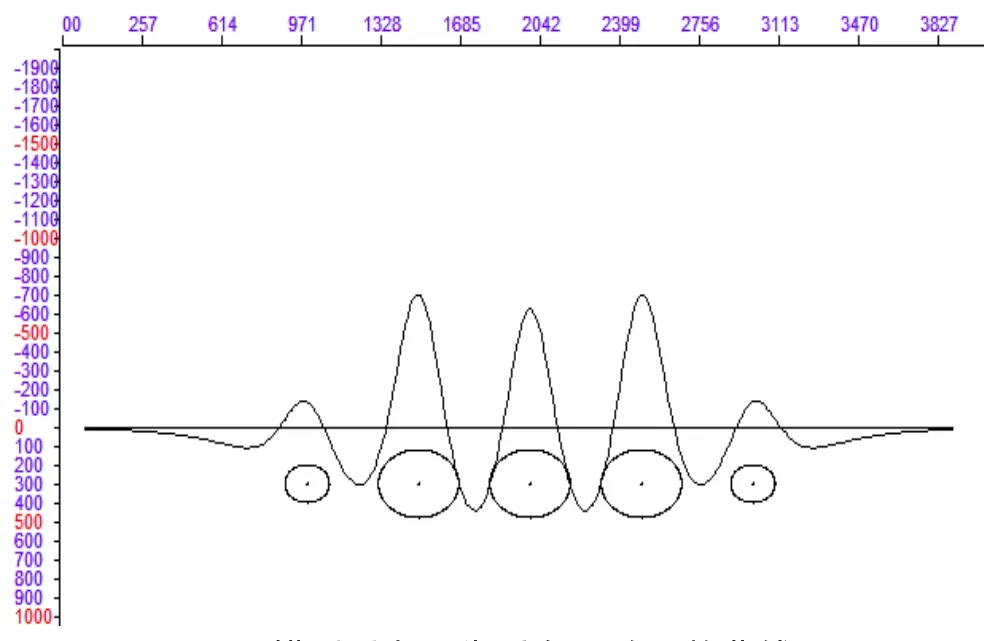
图8 模型重力异常垂向二阶导数曲线图

图9 模型重力异常曲线图

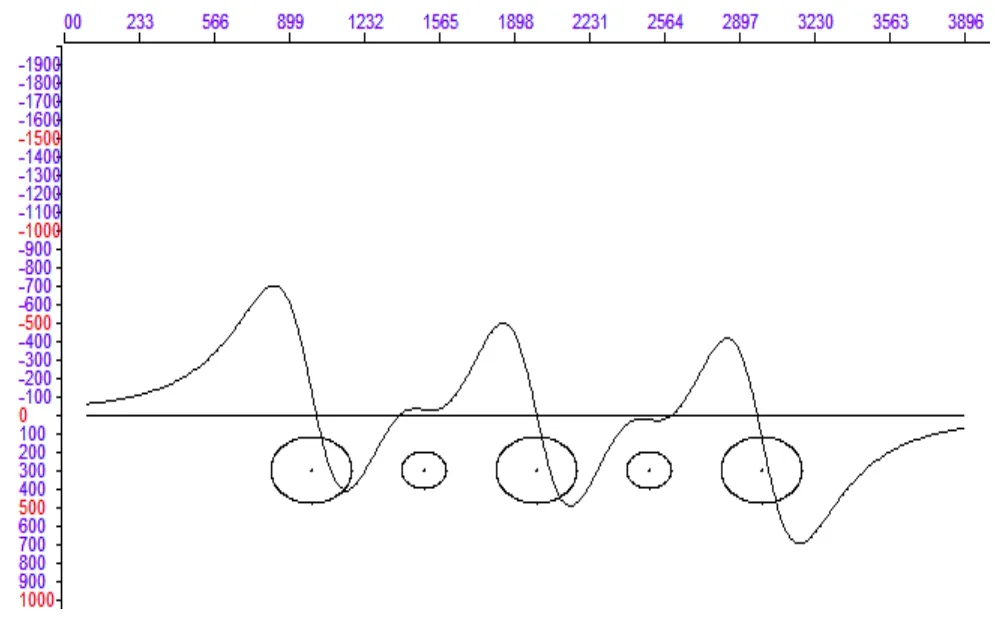
图10 模型重力异常水平一阶导数曲线图

图11 模型重力异常垂向一阶导数曲线图

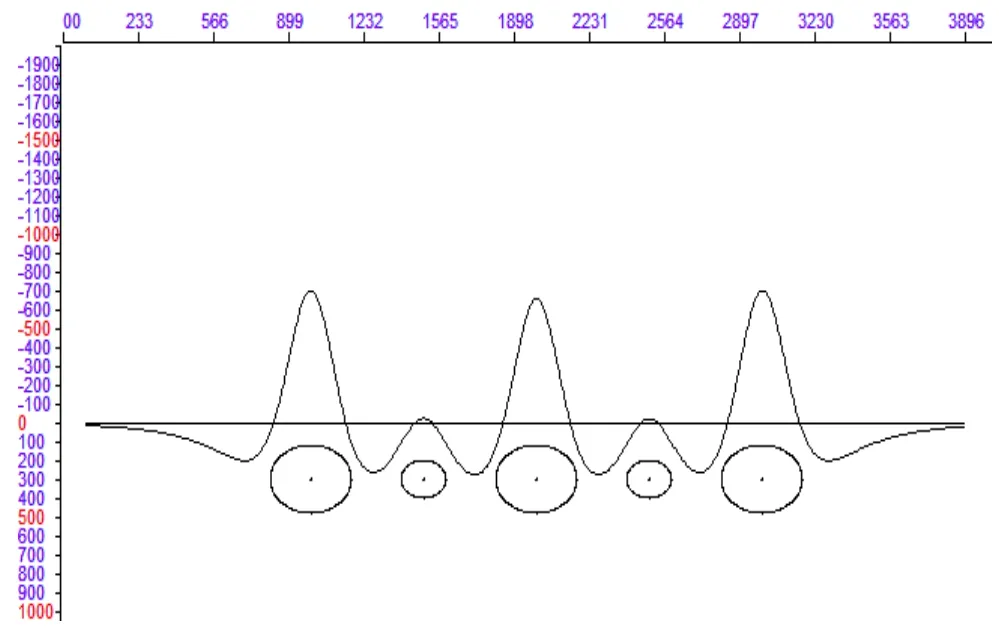
图12 模型重力异常垂向二阶导数曲线图

2.1.4 半径、埋深均不相等的圆柱体

模型为沿X向依次排列多个中心埋深，截面圆心距相同均为500m，半径均不相等的均匀圆柱体，剩余密度均为2.67g/cm3。半径小的圆柱体截面半径均为100m，埋深为150m，半径大的圆柱体截面半径为180m，埋深为400m。模型的重力异常、水平一阶导数、垂向一阶导数和垂向二阶导数的剖面曲线图分别如图 13～16。

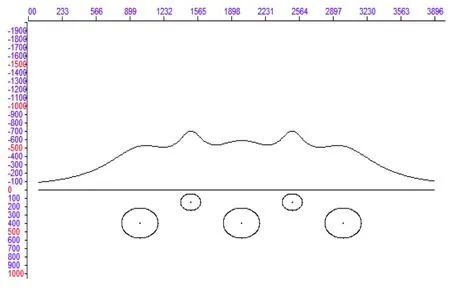
图13 模型重力异常曲线图

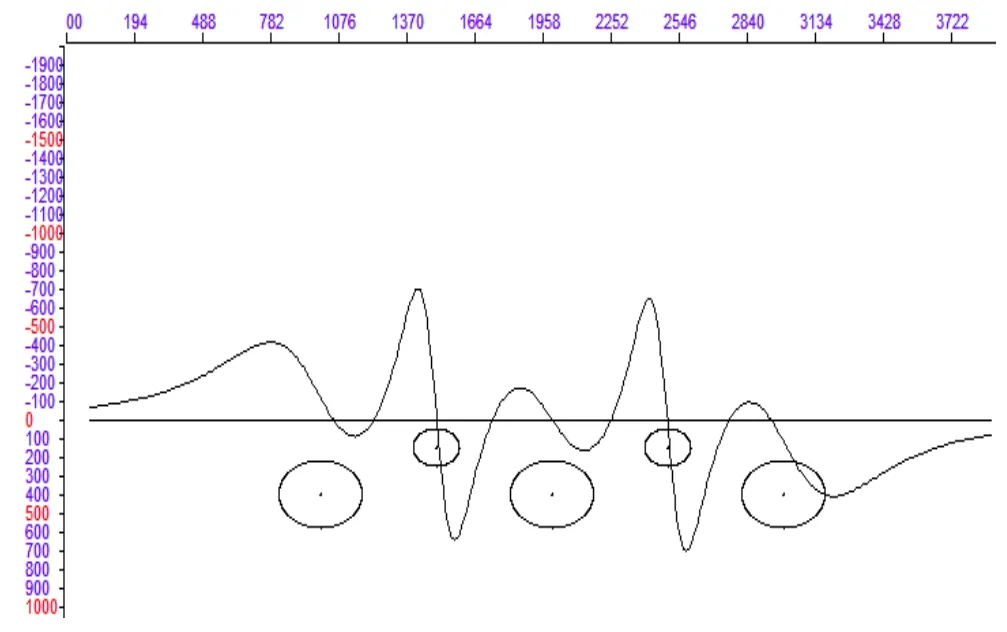
图14 模型重力异常水平一阶导数曲线图

由前面四种模型，可以得出：圆柱体所产生的重力异常水平叠加的影响，从重力异常曲线上不能得到重力异常是由多个圆柱的水平叠加的结果以及模型圆柱体的位置，也使得重力异常水平一阶导数曲线图的零值点极不容易确定模型中每个圆柱体的位置。重力异常水平一阶导数及二阶导数异常的曲线却能够把模型中圆柱体所产生的叠加异常准确地划分，增加导数的阶次可以使得模型重力异常曲线的极值幅度变小，增强了对模型中圆柱体的分辨能力，这种能力的增强正好说明了高阶导数能够分辨相互靠近的叠加异常。

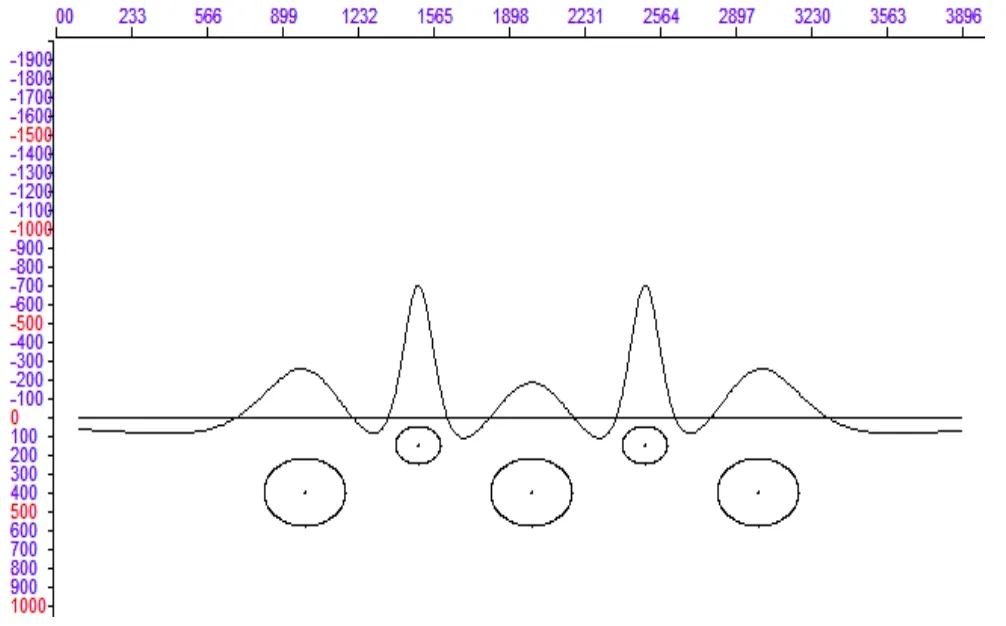
图15 模型重力异常垂向一阶导数曲线图

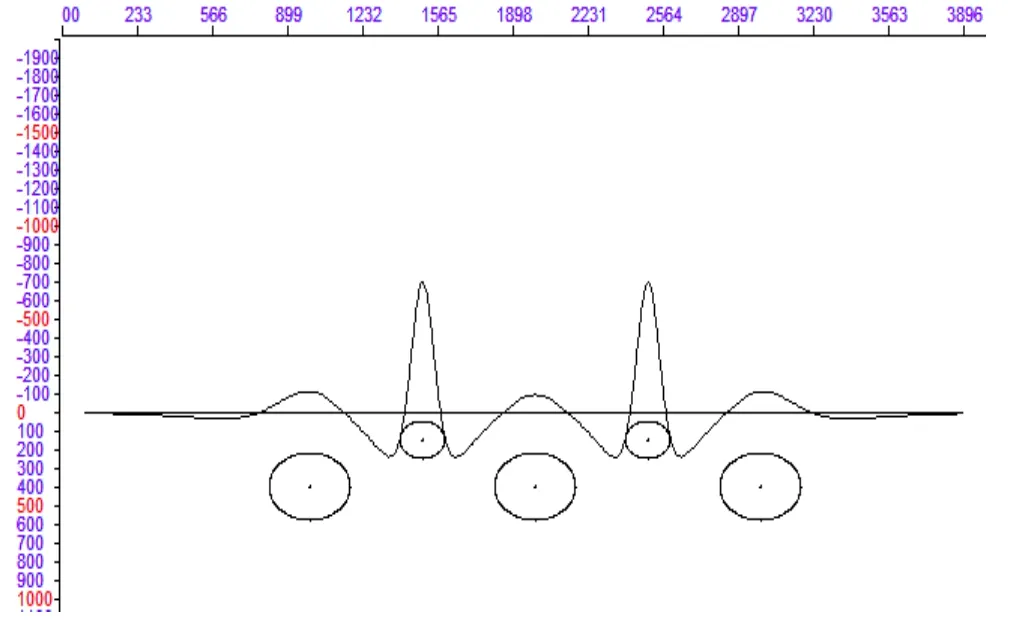
图16 模型重力异常垂向二阶导数曲线图

2.2 多边形模型

2.2.1 单个矩形体

模型是剩余质量均匀分布的矩形体，测线长度为200m，测点距离为1m，剩余密度为2.67g/cm3，模型是中心点在测线中心的矩形：模型的中心点坐标为100m，中心埋深为75m。

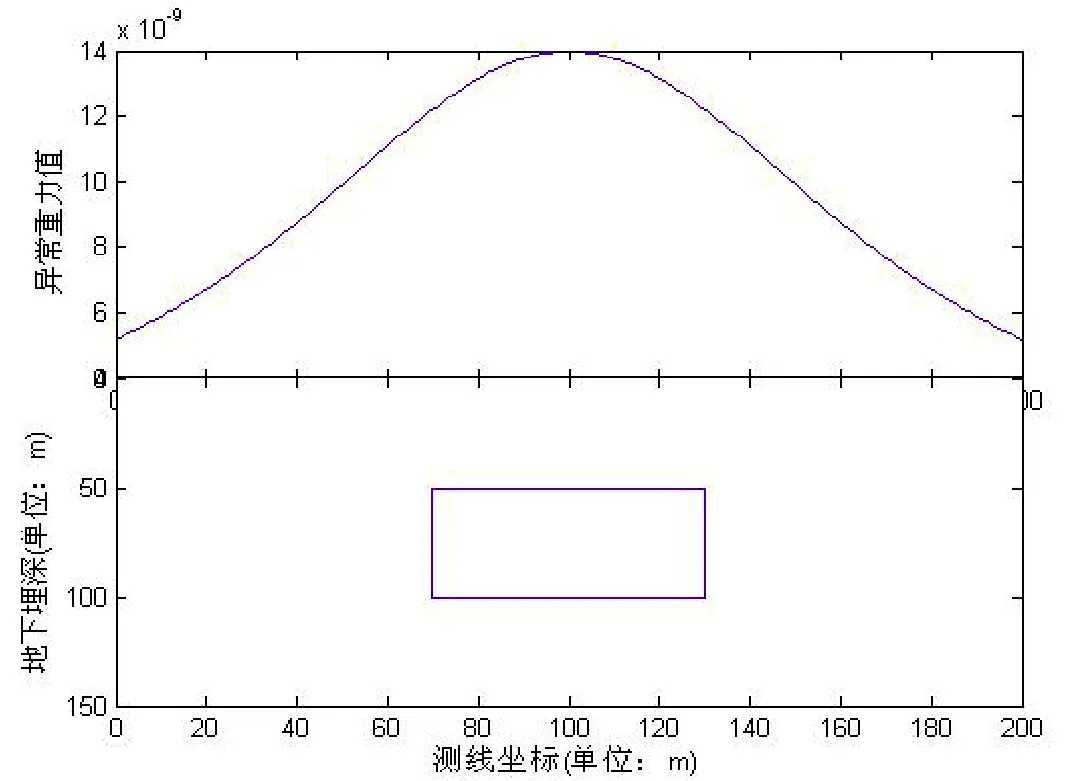
图17 模型重力异常曲线图

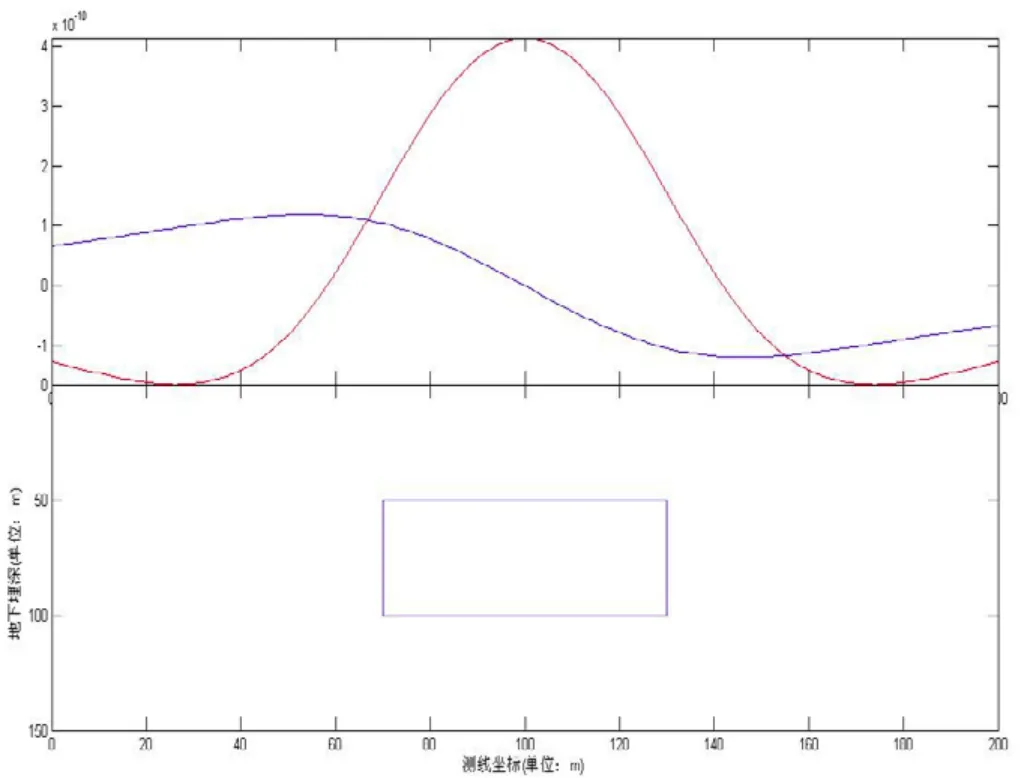
图18 模型重力异常x与z方向一阶导数曲线

2.2.2 埋深不等，大小不等的两个矩形体

模型为不同大小、不同埋深的两个均匀矩形体，测线长度为200m，步长1m，剩余密度为，浅部矩形体的中心埋深18m；深部矩形体的中心埋深125m。

两个模型中的地质体所产生的重力异常都在其中心位置取得了极大值，模型中重力异常的水平一阶导数的零点值以及垂直一阶及二阶偏导的极大值均对应模型中心在地面的投影位置。

3 结论

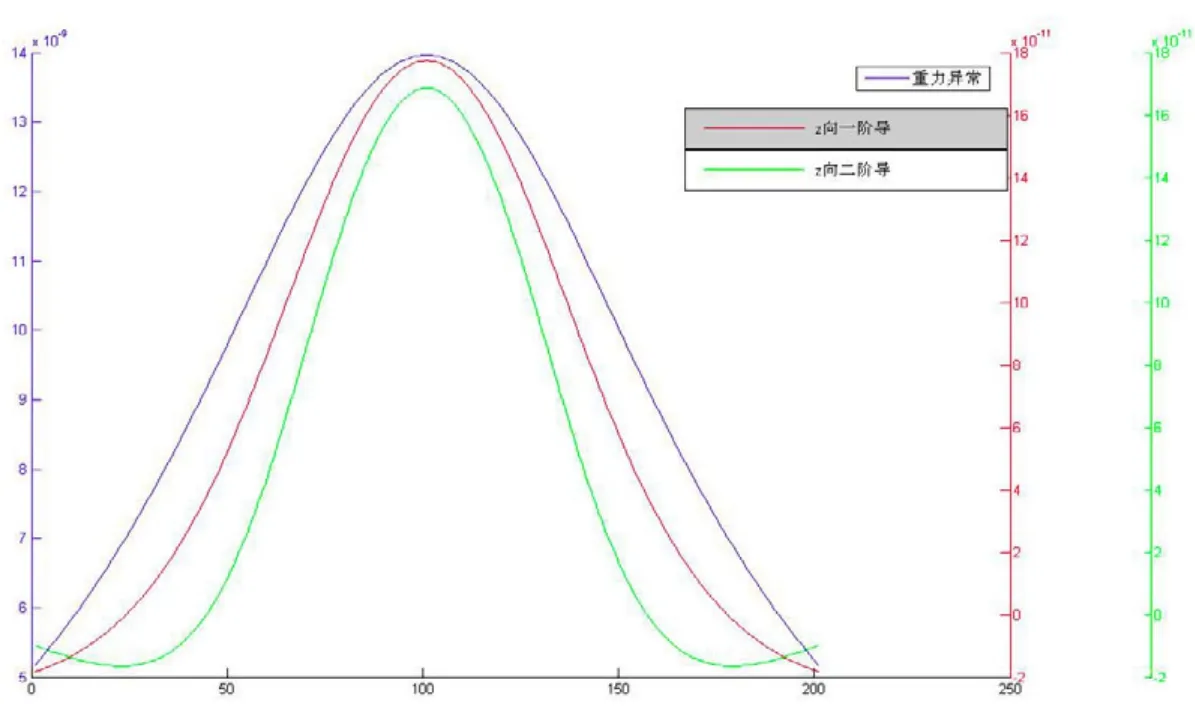
图19 模型重力异常垂向一阶导数与二阶导数曲线对比图

文章选用了由圆柱体、多边形组成的多种模型进行模拟计算，探讨它们的二维剖面异常的变化特征，通过模型的重力异常曲线图、水平一阶导数曲线图、垂向一阶导数曲线图、垂向二阶导数曲线图对比分析，得到以下结论：重力异常的导数在不同形状地质体上有不同的特征，有助于对异常的解释和分类；可以突出浅而小的地质体的异常特征而压制区域性深部地质因素的影响，在一定程度上可以划分不同深度和大小异常源产生的叠加异常，且导数的次数越高，这种分辨能力越强；可以将几个互相靠近、埋深相差不多的相邻地质因素引起的叠加异常划分开来。这些功能主要是因为导数阶次越高，则异常随中心埋深加大而衰减越快，从水平方向来看，基于同样道理，阶次越高的异常范围越小，因而从垂向看或从水平方向看，高阶导数的异常分辨能力都提高了。

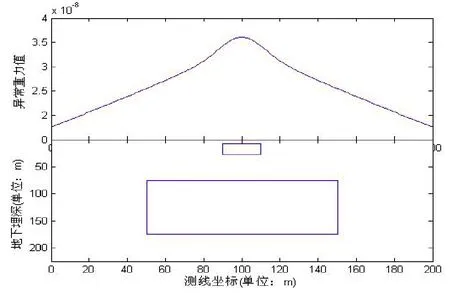
图20 模型重力异常曲线图

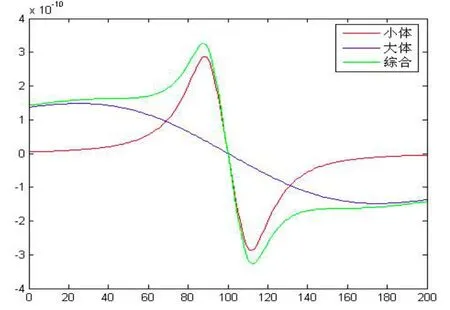
图21 重力异常水平一阶导数曲线综合对比图

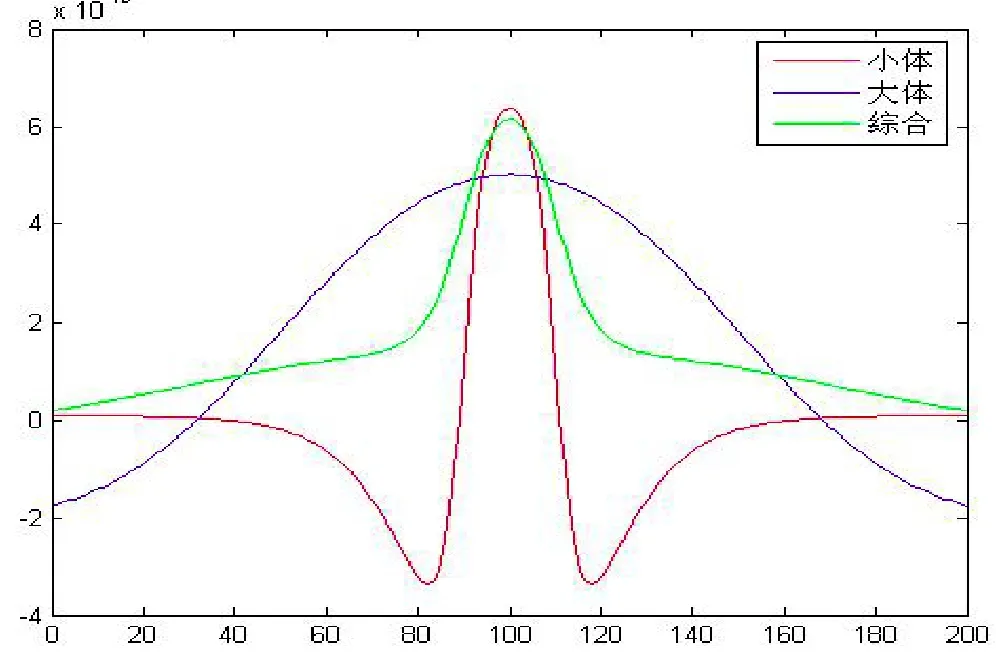
图22 重力异常垂向一阶导数曲线综合对比图

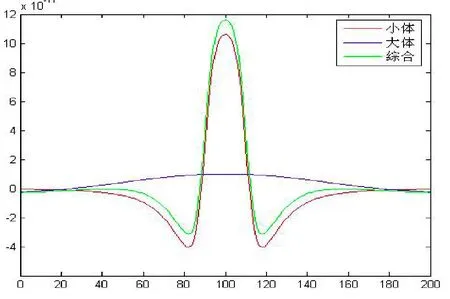
图23 垂向二阶导数曲线综合对比图

[1] ed A. Kham Ies. 对重力势二阶垂直偏导数的一种新的取样方法[J]. 资源调查与环境, 2007，28(4)

[2] 曾华霖. 重磁资料数据处理程序分析[M]. 北京：地质出版社，1985

[3] 何昌礼. 重力异常解释[M]. 成都地质学院，1988

[4] 何昌礼，钟本善. 复杂形体的高精度重力异常正演方法[J]. 物探化探计算技术，1988，10（2）：121～128.

[5] 张风旭. 高精度重力异常数据处理方法--技术研究[Z]. 吉林大学地探学院，2006

[6] 杨辉，王宜昌. 复杂形体重力异常高阶导数的正演计算[J]. 石油地球物理勘探，1998，33(2)