基于DEM的单沟泥石流危险性定量评价

杨 玲，周海波

（1.四川省核工业地质调查院，成都 610061；2.四川省交通运输厅公路规划勘察设计研究院，成都 610041）

白龙江流域地处甘肃南部，主要包括甘南舟曲、迭部，陇南宕昌、武都和文县等行政单元，流域面积约1.80万km2。地理位置上该区属秦岭西段，地处青藏高原、黄土高原和四川盆地交汇处，构造上位于新生代印度－亚洲板块碰撞带变形效应的东部边界，新构造活动极为强烈；同时，该区位于我国南北地震带中北段，地震活动频繁。该区山高坡陡、河谷深切，地表多见黄土和厚层松散堆积物，降雨集中且多暴雨；地表裸露、生态环境脆弱，再加上不合理的人类活动，该区已成为我国四大地质灾害高发区之一。据统计，白龙江流域有泥石流沟700余条，泥石流灾害分布范围广，暴发频率高，危害极为严重。1984年8月3日，整个武都境内普降暴雨，全县400多条沟道爆发泥石流，造成巨大损失。文县主要是由于改建212公路，2001年暴雨激发泥石流灾害，使交通中断40余天，损失严重。此外，众所周知的舟曲“8.8”三眼峪、罗家峪特大泥石流灾害及宕昌“5.13”和“5.31”泥石流灾害事件，造成了大量人员伤亡和财产损失。受汶川大地震的影响，该区山体和岩土结构破坏加剧，松散堆积物剧增，诱发了一系列新的泥石流地质灾害。白龙江流域泥石流类型多，成灾机制复杂，危害严重。国内外的理论分析和工程实践均清晰表明，泥石流地质灾害的发生、发展及空间分布均受控于区域工程地质环境[1]。

1 流域系统信息熵理论

1.1 现有流域系统信息熵模型

熵的概念起源于热力学，熵的运用已经扩展到其他自然科学及社会科学领域。熵是对系统状态的描述，侵蚀等各种地貌过程作用下形成的地表形态也是一种状态，可用熵来描述[2]。美国地貌学家A.N.Srahler于 1952 年提出 Srahler 面积-高程分析法，实现了地貌发育阶段的定量分析；斯特拉勒（Srahler）积分大小能够用来量化戴维斯模型的侵蚀流域地貌演化阶段。我国学者艾南山将反映地貌发展形态的Srahler面积-高程分析法与信息熵原理相结合，提出侵蚀流域系统的地貌信息熵理论及其计算方法。熵值大小可以作为区域水土流失和滑坡、泥石流等自然灾害强弱的定量判定指标[2]。

蒋忠信研究滇西北的金沙江、澜沧江、怒江及其支流河谷纵剖面演化，发现可以用伊凡诺夫(И.В.Иванов)的河流剖面方程描述[2]：

其中，h 和l 分别为纵剖面上某点与河口的高差和水平距离；H和L分别为河源到河口之间的高差和水平距离；N为河谷形态指数。与Srahler曲线相比，没有侵蚀流域的条件限制；在此基础上，艾南山等[3,4]进一步建立了一般流域系统信息熵H1。

蒋忠信[5,6,8,9]认为一般河流流域多呈长宽比甚大的矩形；而泥石流具有狭窄的流通区和庞大的形成区，其典型形态为扇形或菱形小流域。由于泥石流侵蚀速率远比水动力强且下蚀主要在中下游流通区；泥石流淘谷纵剖面演化较迅速；并提出了适合典型泥石流沟的流域系统信息熵H2及泥石流流域系统超熵Hp。

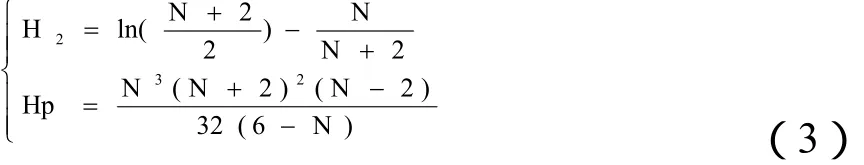
1.2 泥石流沟流域系统信息S计算模型

本研究以现有 DEM数据为基础，结合泥石流野外调查数据；用Arcgis软件提取流域面积—高程信息，拟合泥石流沟的面积—高程函数y=f(x)：

图1 研究区泥石流分布

该模型以泥石流沟谷的高程、面积信息为基础，未直接使用沟谷形态指数N计算流域系统的信息。通过对研究区252条泥石流沟的流域面积与主沟长度的统计分析，验证了流域面积与主沟长度存在函数关系（公式6），具有较强的相关性；即流域面积与高程，主沟长度与高程均能体现流域地貌信息。

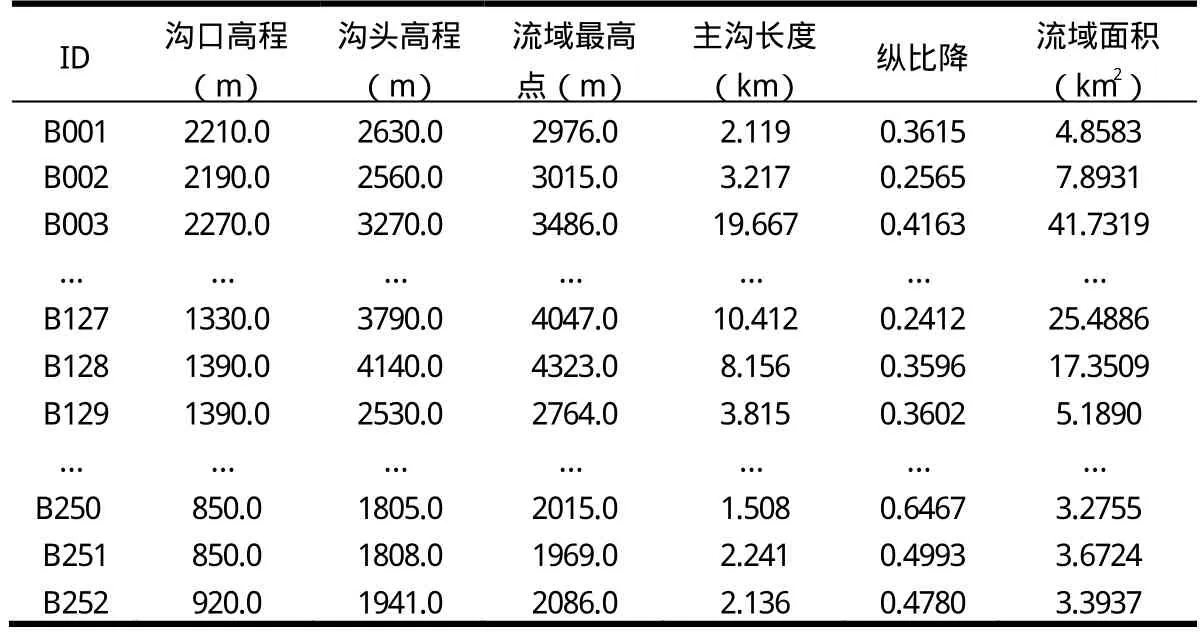
表1 泥石流沟基本特征参数

2 研究区与研究数据

研究区域主要是甘肃南部地区白龙江流域；涉及迭部、宕昌、舟曲、武都及文县等县区。泥石流沟主要分布在白龙江主河道宕昌县—舟曲县段，舟曲县—武都县段及武都县—文县段，尤其舟曲—武都区段泥石流最发育；作者在野外实地调查的基础上，收集整理了252条泥石流沟流域特征基本参数，主要是泥石流沟沟口高程，沟头（源）高程，主沟长度，主沟纵比降及流域面积等（图1，表1）。

对获取的252条泥石流沟的基本特征参数进行统计分析；经计算得到其主沟长度、主沟纵比降及泥石流沟流域面积的统计直方图。经过分析；研究区泥石流主沟长度集中在0～10km，约占82.94%；其中1～ 7.5km的泥石流沟约占76.98%。泥石流主沟的纵比降集中在0～0.6，约占96.43%，其中纵比降在0.15～0.60，约占94.05% 。泥石流沟流域面积集中在0～25km2，约占80.95%；其中流域面积在1～25km2的约占68.25%。

根据实地调查情况，选择了45条具有代表性的泥石流沟。同样对其进行统计分析；通过其统计直方图可知，所选45条泥石流沟的主沟长度集中在1～7.5km，约占82.22%；主沟纵比降集中在0.15～0.60，约占86.67%；流域面积在1～25km2约占75.56%。由于主沟长度或流域面积较大的泥石流沟危害性较大，对其做重点研究。

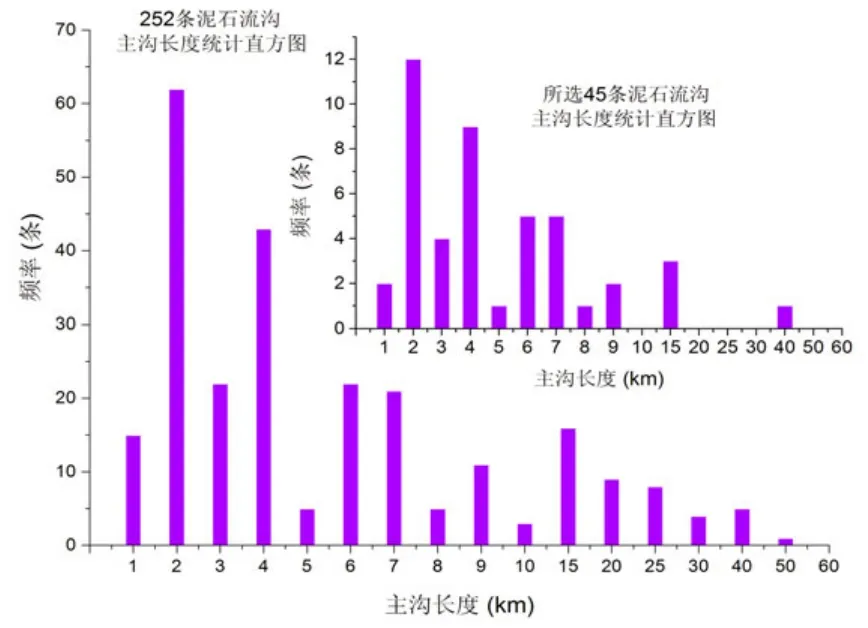
图2 泥石流沟的主沟长度统计直方图

图3 泥石流沟的主沟纵比降统计直方图

图4 泥石流沟流域面积统计直方图

图5 泥石流流域面积与主沟长度函数关系图

另外，对研究区泥石流域面积，主沟长度和主沟纵比降进行统计分析，其流域面积与主沟长度有较强的相关性(图 5)，两者之间存在幂函数关系（公式 6）。

3 泥石流流域系统信息实例分析

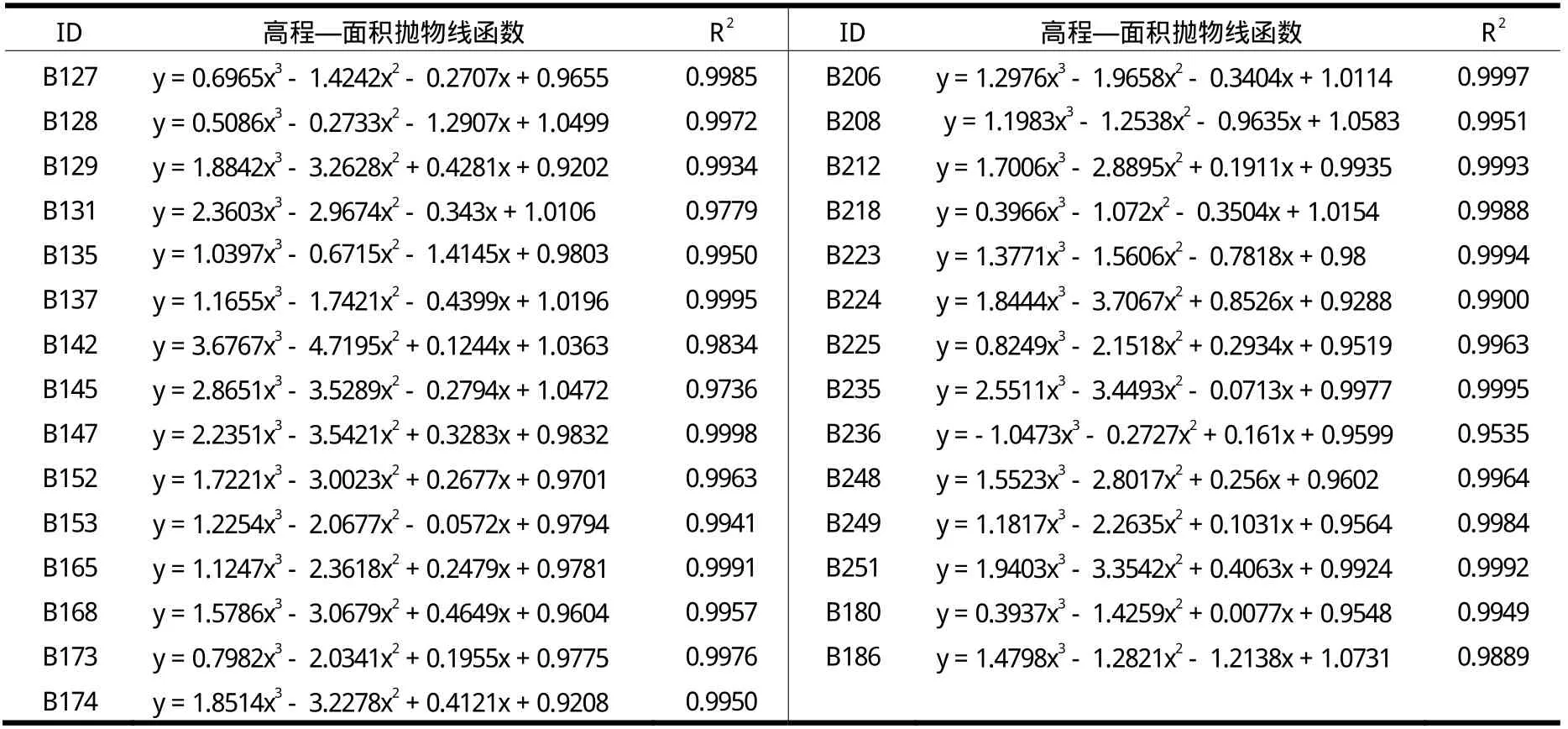
以DEM数据为基础，使用ArcGIS软件获取所选的45条泥石流沟的主沟高程—面积抛物线；然后利用SPSS对其沟谷高程—面积抛物线进行函数拟合；经计算得到45条泥石流沟单沟高程—面积抛物线的拟合函数（表2）。计算泥石流单沟高程—面积抛物线的拟合函数时，应确保f(x)≥0，x∈[0,1]。

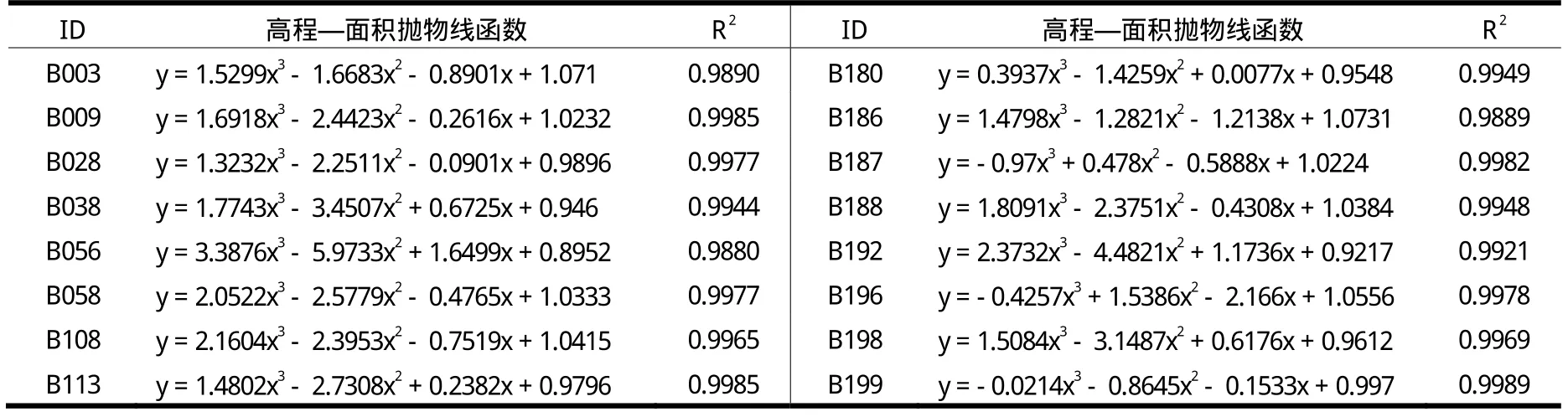
表2 泥石流流域高程—面积抛物线函数

?

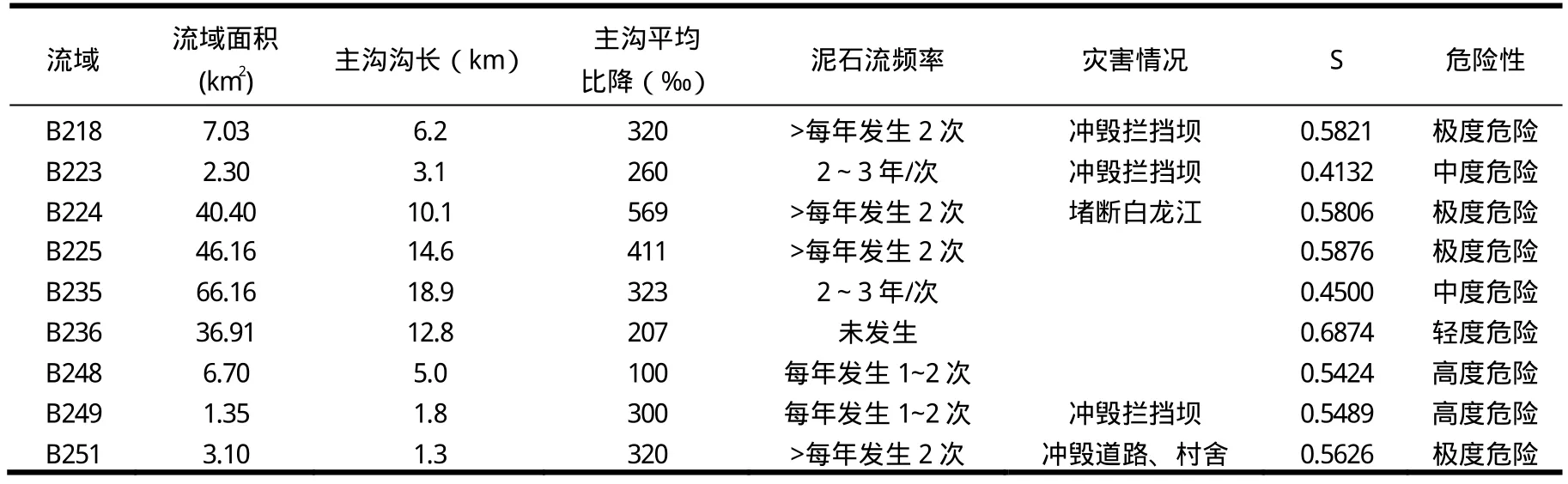
在拟合出单沟泥石流高程—面积抛物线函数的基础上，使用Matlab中的积分函数int，结合泥石流流域系统信息S计算模型（公式 4 ，5），计算出45泥石流沟流域系统信息S（表 3）。

表3 泥石流沟流域系统信息值

?

4 理论应用分析—泥石流危险性定量评价

泥石流沟流域的地貌特征对泥石流的发育、发展以及衰退都有较强的影响。流域的相对高度决定流水势能的大小，为松散碎屑物质的起动提供动能；泥石流主沟长度与流域面积密切相关（公式6），且均是泥石流发生的重要因素；其中流域面积所接受的降水量是决定沟谷水动力条件的主要参数[11]。因此，对沟谷（侵蚀）地貌特征可以在一定程度上反映泥石流的发育阶段，并判断其危险程度。

蒋忠信将泥石流发育的全过程划分为两个地貌期和5个地貌阶段[7,9,10]（表4）。随着侵蚀流域地貌演化，不同地貌阶段的泥石流发生的可能性也在不断变化。总体上，泥石流发育期的三个地貌阶段，泥石流危险性大；当泥石流演化到衰退期，泥石流危险性随地貌演化而逐步减小。根据泥石流沟流域不同地貌阶段的特点，根据泥石流流域系统信息将其危险性划分为5个等级；其信息值在一定程度上定量描述了泥石流沟危险性。即泥石流流域系统信息值S能够作为泥石流危险性的一种定量化指标。

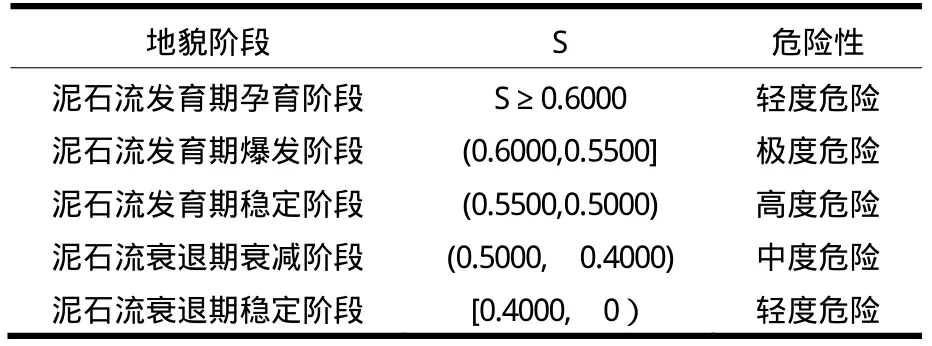
表4 泥石流地貌阶段与危险性划分

5 结论与讨论

目前，现行（单沟）泥石流危险性评价方法考虑影响泥石流形成的各环境因子，但没有考虑各环境因子的综合影响（流域地貌特征整体状态）；另外，受限于现有数据，部分泥石流沟危险性评价模型所需特征参数较难获取，其使用产生局限性。

泥石流是自然界中一种水土流失现象；也是一种重要的促进地貌演化的侵蚀作用。有利的地形地貌基础及丰富的补给物质条件是泥石流发生的必要条件，也是泥石流沟流域存在的一种状态；这种状态对泥石流形成和发展有重大影响。

DEM是地表形态的数字表达，也是地貌形态的一种定量化描述。在缺乏泥石流流域内基本环境因子定量化数据的情况下，以 DEM数据为基础，计算其流域系统信息，可以作为泥石流危险性定量化评估的一种指标。但目前，地貌信息用于泥石流危险性评价的应用较少，其理论和方法需要不断完善。

[1] 宁娜, 马金珠. 基于GIS和信息量法的甘肃南部白龙江流域泥石流灾害危险性评价[J].资源科学，2013, 35(4): 892～899.

[2] 艾南山. 侵蚀流域系统的信息熵[J]. 水土保持学报, 1987, 1(2): 1～8.

[3] 艾南山, 岳天祥. 再论侵蚀流域系统的信息熵[J]. 水土保持学报, 1988, 2(4): 1～9.

[4] 岳天祥, 艾南山, 张英保. 论流域系统稳定性的判别指标—超熵[J]. 水土保持学报, 1989, 3(2): 20～28

[5] 蒋忠信. 滇西北三江河谷纵剖面的发育图式与演化规律[J]. 地理学报, 1987, 42(1): 16～27

[6] 蒋忠信. 矩形流域地貌信息熵的探讨[J]. 水土保持通报，1989, 9(6): 83～87

[7] 蒋忠信. 泥石流沟谷演化的不等时距灰色预测[J]. 地理研究，1994,13(3):53～59

[8] 蒋忠信. 泥石流沟谷纵剖面形态与流域地貌信息熵[C]. 地质灾害国际交流论文集, 西南交通大学出版社, 1993

[9] 蒋忠信. 泥石流的沟谷纵剖面形态与流域系统超熵[J]. 科学技术通讯，1994(4): 1～6.

[10] 蒋忠信. 泥石流流域系统的超熵[J]. 中国地质灾害与防治学报，1992,3(1): 33～40

[11] 王晓朋，潘懋，任群智. 基于流域系统地貌信息熵的泥石流危险性定量评价[J]. 北京大学学报（自然科学版）,2006,1（3）:1～5