基于参数辨识的大型航天器自适应角动量管理*
朱孟萍,徐世杰,陈新龙,李 志,江 玲
(1.中国空间技术研究院钱学森空间技术实验室,北京100094;2.北京航空航天大学,北京100191)
0 引 言
控制力矩陀螺(CMG,control moment gyro)无工质消耗、输出力矩大,是大型航天器的理想干扰力矩执行机构.长期在轨飞行,CMG需要吸收较大环境时,角动量迅速达到饱和,需要频繁卸载.传统卸载方案是用推力器卸载,这种方法会带来工质的不断消耗.另一种途径是磁力矩器卸载,但其卸载能力有限,不能满足大扰动力矩下的卸载需求.考虑到环境扰动力矩大部分与姿态有关,为此可以对航天器进行姿态控制/角动量管理(ACMM,attitude control/momentum management)一体化控制,通过调整航天器姿态指向使引起CMG积累的气动力矩、引力梯度力矩、陀螺耦合力矩等扰动力矩相互抵消,从而使CMG角动量基本不积累.
ACMM控制器的设计的任务便是如何建立航天器姿态和CMG角动量之间的平衡.最早的ACMM控制器是线性控制器,有静态[1]和动态[2-3]之分.静态线性化指航天器系统方程在固定姿态处线性化.动态线性化中线性化点是系统当前TEA,线性控制器设计简单,但控制效果很大程度依赖于线性化点的选取.当系统力矩平衡姿态(TEA,torgue eguilibrium)远离线性化点时,控制器无法成功完成任务.Lee[3]基于那什博弈论,Flasher等[4]基于神经网络,Zhu等[5]采用状态相关黎卡提方法设计的非线性自适应或鲁棒控制器不存在线性化带来的误差问题,可以通过不断调整控制参数保证姿态和角动量之间的动态平衡,但控制器结构相对复杂,在线计算量大.
跨越了线性和非线性界线的反馈线性化方法与传统利用泰勒展开局部线性化的方法相比,线性化过程中没有忽略任何非线性项,对变换有定义的整个区域都适用.Sheen等[6]基于该理论设计的控制器解决了传统线性ACMM控制器对平衡姿态敏感的问题.但该控制器的局限是需要准确的航天器惯量信息,当航天器惯量存在不确定性时,无法精确线性化,影响控制系统性能.
为弥补以上反馈线性化方法对转动惯量的依赖,本文设计了带有在线参数辨识的自适应ACMM控制器.该控制器由两部分构成:在线参数辨识回路和反馈线性化控制回路,其结构如图1所示.
反馈线性化回路通过状态变换和输入变换,将原非线性系统转化为等价线性系统,对等价系统设计线性控制律,然后通过输入变换的逆变换求解原系统的非线性控制律.在线辨识回路以闭环控制力矩作为激励,结合系统的角速度响应进行辨识,避免了外加激励设计不当导致的大幅度姿态漂移.此外,由于系统位于TEA时,外力矩相互抵消,CMG输出的控制力矩较小,无法保证传统最小二乘法的持续激励要求.为此辨识算法采用具有有界增益遗忘因子的最小二乘法[7],该算法在激励不持续时仍具有有界增益,而且收敛快,能够跟踪时变参数.
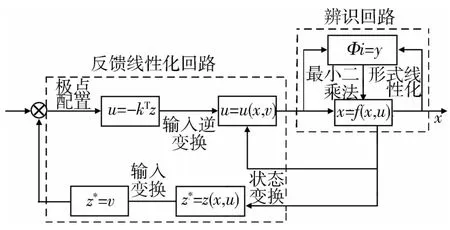
图1 控制器结构图Fig.1 Controller structure
1 ACMM数学模型
本文参数辨识和角动量管理分别在本体坐标系和轨道坐标系下进行.
1.1 本体坐标下动力学方程

式中,Ib和ωb分别为体坐标系下航天器转动惯量和系统惯性角速度分量,分别为 CMG输出的控制力矩、引力梯度力矩和大气扰动力矩,为陀螺非线性耦合项.由于大气扰动无法精确获得,控制器设计中暂不考虑其影响.

式中,ω0为轨道角速度,为地心到航天器质心的单位矢量.
1.2 轨道系下动力学方程
本体坐标系到轨道系坐标转换矩阵的导数为

转动惯量在本体坐标系与轨道系间的关系式为

航天器绝对角速度在轨道系下可以表示为

将式(6)对时间求导,并将式(1)和(4)代入,利用式(4)和(5)简化后得到动力学方程


CMG角动量的动力学方程为


2 反馈线性化控制器设计
2.1 坐标变换
Sheen等[6]通过阶数分别为4,3,2的3个输出量定义的坐标变换将ACMM系统(10)转化为第一规范型,但选择的输出变量的物理意义不明显.为在姿态稳定前提下有效避免角动量积累,将CMG角动量和姿态信息同时作为输出变量,考查系统总角动量

对Ho三轴分量分别求2阶,2阶以及3阶Lie导数


定义如下新状态:

新状态方程为


2.2 输入变换
据已有研究[6],ACMM系统满足反馈线性化的必要条件是状态方程(22)中E(x)可逆,此时对新状态方程(22)做如下输入变换:
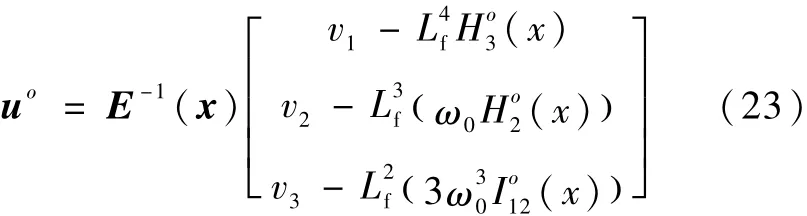
则系统(22)等价为以下线性系统:

其中,v为线性系统输入.
2.3 等价线性系统设计
(1)期望轨迹设计
仅考虑引力梯度力矩以及陀螺耦合力矩的影响时,定义ACMM系统的平衡姿态为狭义TEA,记X*为变量X在平衡姿态处的状态值.

根据式(11)知TEA处的系统总角动量为


(2)线性跟踪控制律设计
系统(24)具有线性输入输出关系,希望其输出跟踪期望轨迹zd时,可设计相应的线性控制律为
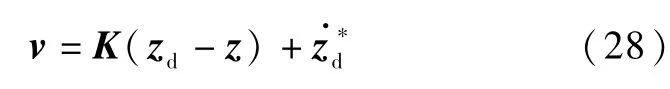
2.4 反馈线性化控制律求解
联立式(23)和(28)得到将ACMM系统精确线性化所需要的最终控制律

2.5 控制律奇异性分析
由式(22)知,非线性状态变换有效的前提是E(x)非奇异.由E(x)表达式知可逆性取决于的可逆性,根据Ip和Io之间的转换关系,可知的可逆性由上式决定:
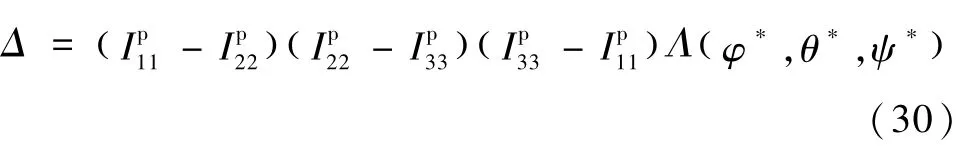
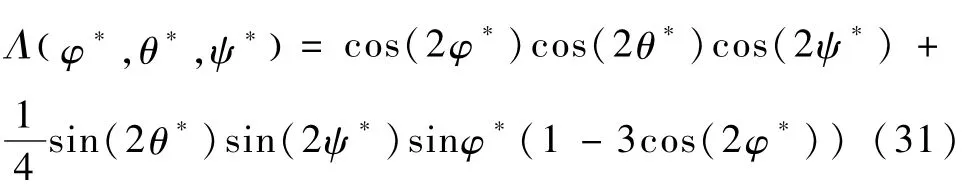
满足以下两条件时Δ≠0

条件(32)为物理条件,给出了控制律(29)对转动惯量的约束;条件(33)限制了控制律适用的姿态范围.
(1)转动惯量约束
惯量约束(32)是ACMM系统的固有特性,即使对于线性控制器,约束同样存在.例如,取本体坐标系为惯性主轴坐标系,在零姿态处线性化的系统方程俯仰与滚动/偏航解耦.对俯仰通道,取状态变量为,则其状态方程为


(2)姿态约束
3 参数辨识
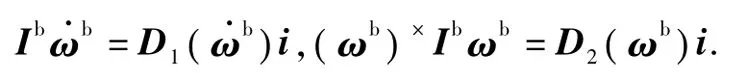
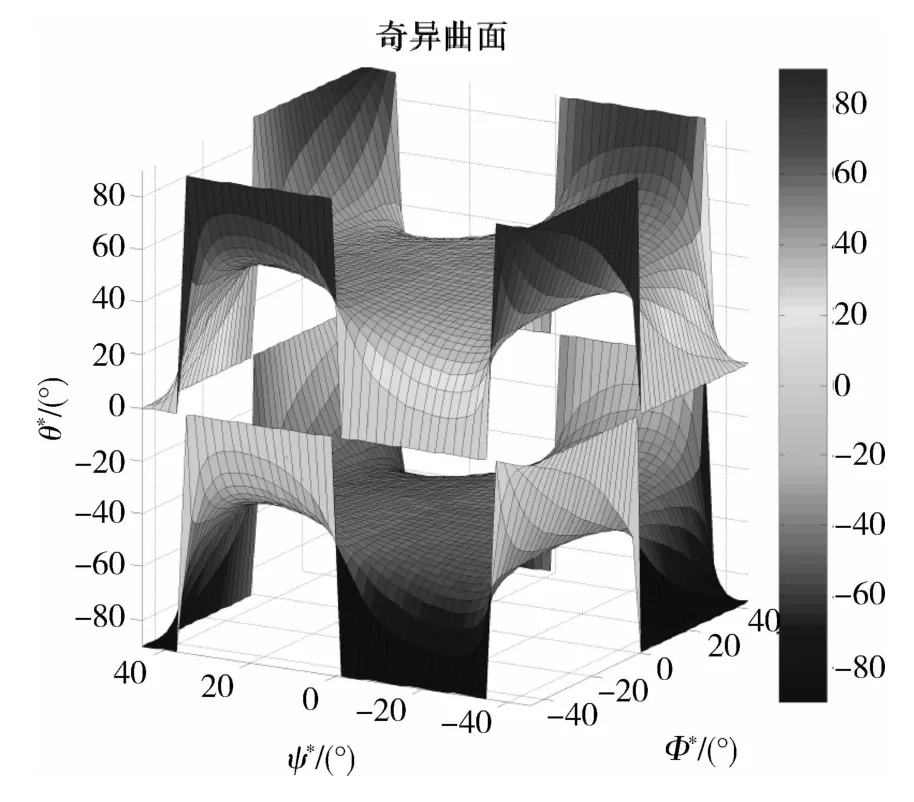
图2 Θ*=[ 0 0 0]T附近的奇异曲面Fig.2 Singularity surface nearΘ*=[ 0 0 0]T
式中,

根据以上关系式,动力学方程(1)转化为

将式(35)左右两边积分,并写为线性最小二乘标准形式Φi=y,有

系统位于TEA时,外力矩相互抵消,控制力矩较小,无法满足传统最小二乘法的持续激励要求,为此在迭代过程中增加有界增益遗忘因子[8],保证估计器在激励不持续时仍具有有界增益.
4 数学仿真
以空间站组合体舱段转移过程为例验证控制器性能.假设空间站组装过程中通过机械臂将实验舱从节点舱轴向对接口转移到侧向对接口.采用简化模型,不考虑柔性及机械臂动力学特性,仅考虑实验舱运动带来的转动惯量摄动,系统转动惯量的变化如图3所示.转移中通过核心舱的一套五棱锥构型的CMG进行整个系统的控制,其角动量包络上的最小角动量为4 200 N·m·s.假设转移开始时空间站处于对地定向姿态,初始姿态为:

图3 系统转动惯量变化历程Fig.3 Moment of inertia history
控制器的角动量管理能力如图4~5所示.整个转移过程中CMG的角动量都被严格控制在其容量范围以内.由于转移过程中核心舱与实验舱的相对运动主要位于偏航方向,所以核心舱的TEA也主要体现在偏航轴上.等价线性系统的9个状态变化历程如图6所示,其中除第5个状态需要跟踪时变的参考输入以及第8个滚动/俯仰惯量积在转移过程中不断变化外,其它幅值波动较小,动态效果比较理想.
作为对比,用传统的线性二次型(LQR)控制器[1]对以上系统进行了仿真,结果分别如图7和图8所示.可以看出,对以上惯量变化明显的系统,传统的线性控制器无法成功避免CMG角动量的饱和.

图4 姿态角响应Fig.4 Attitude response

图5 CMG总角动量Fig.5 CMG momentum history

图6 等价线性系统状态变量Fig.6 States of the equivalent linear system

图7 LQR控制器下的姿态角响应Fig.7 Attitude response under LQR controller

图8 LQR控制器下CMG总角动量Fig.8 CMG momentum history under LQR controller
5 结 论
为抑制参数不确定性对ACMM控制器性能的影响,设计了带有参数辨识的间接自适应控制器.该控制器基于反馈线性化理论,不需要解耦,能够在姿态指向与陀螺角动量间实现良好折中.与传统线性控制器控制力矩相比,该控制方案不依赖线性化点的选取,对航天器惯量不确定性具有很强鲁棒性.
[1]WIE B,BYUN K W,WARREN V W,et al.New approach to attitude/momentum control for the space station[J].Journal of Guidance,Control and Dynamics,1989,12(5):714-722.
[2]PARLOSA G,SUNKEL J W.Adaptive attitude stability and control for space station/orbiter berthing operations[C]//AIAA Guidance,Navigation and Control Conference.Hilton Head:American Institute of Aeronautics and Astronautics,2007:913-923.
[3]LEE A C.Robust momentum manager controller for space station applications[D].Rice University,Houston,USA,2003.
[4]JAMES F,RAKTIM B,VADALI S R.Spacecraft momentum management and attitude control using a receding horizon approach[C]//AIAA Guidance,Navigation and Control Conference.Hilton Head:American Institute of Aeronautics and Astronautics,2007:1-22.
[5]ZHU M P,XU S J.Stability-based SDRE controller for spacecraft momentum management[J].Acta Astronautica, 2013, 89(1):71-82.
[6]SHEEN J J,BISHOP R H.Spacecraft nonlinear control[J].Journal of Astronautical Sciences, 1991, 42(3):361-377.
[7]JIANG L,XU SJ.An on-orbit mass properties identification algorithm for large space structures[C]//The 63thInternational Astronautical Congress.Captown:The International Astronautical Federation South Africa,2011:1-9.
[8]SCOOT J P,ROBERT H B.Adaptive nonlinear attitude control and momentum management of spacecraft[J].Journal of Guidance, Control and Dynamics, 1997, 20(5):1025-1032.

