卫星控制系统时序建模分析方法研究*
王 磊,袁 利,戴居峰
(北京控制工程研究所,北京100190)
0 引 言
时序是具有时间约束的实时系统工作流,包括为完成实时系统的功能和性能要求而设计的逻辑执行的过程顺序以及与时间的关系.卫星控制系统的时序是分布于控制分系统与其他分系统之间、控制分系统各单机产品之间、软件和硬件之间、各软件配置项之间以及应用软件中的逻辑要求与时间要求的集合.时序不合理将可能导致卫星控制系统在轨发生控制混乱或故障.由于时序问题具有一定的概率性和隐藏性,因此在设计阶段进行时序分析,验证时序设计的合理性和正确性是必不可少的工作,时序分析的结果同时还可以指导后续的系统测试.
国外卫星控制系统的时序设计有较为成熟的方法和工具.ESA采用对象方法[1]对时序进行建模、分析和设计.1987年,ESA采用了HOOD(hierachical object oriented language)设计方法,1995年,法国航天局将之升级为HRT-HOOD(hard real time HOOD),支持对可调度性的直接分析,广泛应用于ESA的卫星控制分系统嵌入式软件.例如Olympus卫星[2]的控制软件包括周期任务、非定期任务、硬实时任务、软实时任务、后台任务和总线通讯任务,使用HRT-HOOD方法对时序过程进行了四级分解.使用DMSA(deadline monotonic scheduling analysis)方法对每一个任务进行了分析,确认在指定的优先级序列的情况下是否可以使得每一个任务在指定的时间点或允许的时间范围内被运行.在分析过程中,遇到的最大问题是总线中断的处理.最初使用了一个非周期性的对象和一个被动对象来实现中断处理,在中断的时候由被动对象读取数据,而由非周期对象来处理数据,分析表明不能满足指定的时间要求,因此通过修改设计,让非周期对象将数据存放在缓冲区内,通过一个周期对象以固定的频率搬移数据来实现.
模型驱动的分析与设计方法[3-4]是采用模型作为系统设计开发各个阶段的统一描述,通过自动化工具保证各个设计阶段的一致性的方法.2003年美国军方推出了结合部分UML2.0符号库的结构描述语言AADL[5-6](avionics architecture design language),在整个航天业界得到了推广应用后,AADL的含义变为architecture analysis&design language,成为模型驱动方法的主流规范.AADL主要功能是对嵌入式系统的实时性、嵌入式容错、安全分区和动态认证等非功能属性进行建模;能够描述系统的任务调度、任务通讯、分布式多处理器以及嵌入式硬件基本结构等其他性质.可应用在系统的整个生命周期对其进行建模和分析,并针对系统的关键特征,通过一套可扩展的符号系统及其工具框架提供各个开发时期的验证.不仅可以用来对已有系统进行建模和分析,还可以用来设计和整合新的系统,并支持从多种结构观点进行设计、建模和分析.目前欧洲发展的HRT-HOOD体系已开始兼容AADL,最终将转换到模型驱动设计方法.
无论是对象方法还是模型驱动方法,其建模的目的主要是为了在动态平台上运行系统模型来对时序进行分析验证.这两种方法均离不开时序过程的数学描述,因此,必须对时序过程进行数学建模,求得时序参数,才有可能对时序模型进行验证.
国内卫星控制系统在时序设计与分析方面还没有成熟的方法和工具,数学建模分析仅限于局部,在实践中主要是结合型号工作经验通过试错法(try and error)调整时间参数.
本文提出针对时序设计的系统性的数学建模分析方法,明确了时序设计的分解分配过程,给出了时序描述的工作流图方法.
1 任务分析与软硬件协同设计
1.1 任务分析
任务分析是开展系统级时序设计的先决条件.通过任务分析,应得到系统级时序设计的目标和约束条件集合.目标主要包括控制方案对时序的要求、与其他分系统之间工作分工对时序的要求.
结合系统详细技术设计,可能的约束条件包括:系统产品配置、计算机与各单机(敏感器和执行机构)的工作分工与从属关系、各单机(选用的现有产品)工作特性以及软硬件工作分工、各软件配置项工作分工、与控制分系统存在软硬件接口的其他分系统的工作特性(特别是时间特性)等.约束条件在数学模型中一般以已知参数代入求解.
1.2 软硬件协同设计
系统级时序设计首先需要对软硬件功能进行划分,完成软硬件的协同设计.根据系统体系结构、质量体积和功耗约束、电子线路目前的设计水平、计算存储和通信能力等系统约束条件进行综合分析后,重点在上电与切机、通信接口传输机制、缓冲配置、中断、时钟等软硬件密切配合的项目用工作流图描述软硬件工作界面,分别给出软硬件时序设计目标.
2 时序过程的数学建模
2.1 时序分解模型
系统时序设计是对系统时序设计目标分层分解并逐级分配的过程.在每一层分解过程中,应首先建立分解模型,分解出不同的时序设计子项目,并通过对分解模型的求解,得出对应子项目的设计目标.每一层的输出结果可以使用工作流图表达.
例如,控制周期T是系统级设计目标.其分解模型可以建立如下:

式中:t1为上下文切换(任务调度)时间;t2为所有所需的敏感器信息采集时间;t3为控制算法运行时间;t4为所有控制命令发送时间;t5为在单个控制周期内所有可能发生的中断时间(此为外部中断或系统时钟中断,采集敏感器信息而产生的中断安排在t2中);t6为空闲时间.
因此,分解出来的时序项目至少为6项,而每个子项的设计目标通过ti(i=1~6)表示;各个子项目之间的顺序关系可以用工作流图或任务时序图描述.数学模型的求解是要确定模型中所有参数的数值或取值范围,所依据的首要原则是使得每个参数均在可实现范围内,其次是系统应为优化的.
每个子项目的设计目标可以进一步分解.直至分解到最终每个时序环节的时间参数要求.例如t2可以分解如下:
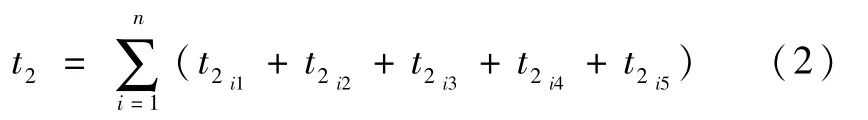
式中:t2i1为AOCC/GNCC向第i个单机发送的信息采集命令的发送与传输时间;t2i2为该单机的响应时间;t2i3为该单机的信息传送时间;t2i4为AOCC/GNCC对该信息的接收和解包处理时间;t2i5为空闲时间(若故障处理要求当前控制周期对该单机的信息采集在一次传输不果后需重传一次,则重传时间计算在t2i5内).若对单个单机有多次信息采集,应累加时间.各个单项之间的顺序关系可以用工作流图描述.
t3可以根据用户需求,分解到控制算法的不同模块.其不同模块之间的顺序关系可以用结构化流程图描述.
t4可以分解如下:
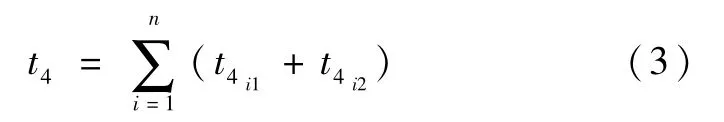
式中:t4i1为AOCC/GNCC向第i个执行机构发送控制命令的发送与传输时间;t4i2为空闲时间(一般设计为0,但当两条命令之间存在同步要求时,同步等待时间计算在t4i2内).若对单个单机有多条控制命令发送,应累加时间.各个单项之间的顺序关系可以用工作流图描述.
t5可以分解如下:

式中:pi是指第i类中断在一个周期内可能发生的最大次数;t00为中断响应时间;t01为中断上下文切换时间;tdi是第i类中断的中断处理时间.
t6可以分解如下:

2.2 时序分配模型
通过时序分解模型可以分解出时序设计的子项目,子项目一般都直接与硬件产品的特性相关,此时,通过进一步细化的数学建模,可以将时序要求分配到具体过程.在时序分配模型中纳入硬件时间特性参数,可以进行正逆数值求解,以得到较优的结果.
例如,设计一个需响应3个外部中断的计算机系统,在优先级确定的前提下,需分析其中断嵌套的情况,得到每个中断的处理时间以及中断发生的频率(两次中断的时间间隔)限制.可以建模如下:
设系统中断响应时间为t00,任务调度的上下文切换时间为t01;中断1(最高优先级)的中断处理时间为t10,产生单次中断的数据包的线上传输时间为t11,两个数据包的最小间隔为t12;中断2(次高优先级)的中断处理时间为t20,产生单次中断的数据包的线上传输时间为t21,两个数据包的最小间隔为t22;中断3(最低优先级)的中断处理时间为t30,产生单次中断的数据包的线上传输时间为t31,两个数据包的最小间隔为t32.
则为保证中断1不丢失数据,需满足:
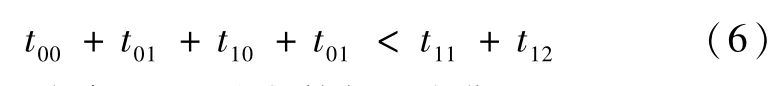
为保证中断2不丢失数据,需满足:

其中,ceil表示向上取整运算.
为保证中断3不丢失数据,需满足:

由上述模型可以看出,为保证各级中断不丢失数据,应采取的措施包括:
1)高优先级的中断处理时间应短于低优先级的中断处理时间;
2)缩短各级中断的处理时间;
3)增大各级中断的两次中断时间间隔.为此,若数据包的线上传输时间较短,则应增大两包数据之间的间隔.
2.3 时序裕度模型
对一段时序过程进行数学建模的最终结果一般表现为一个表达式.由于物理硬件的特性,通常对时间参数的执行结果存在一定的误差,为了保证在最坏情况下仍能满足数学模型,需要进行裕度设计.
设有时间参数T,由若干分段时间参数组成:T为整数.各时间参数用下标l表示取值下限,用下标h表示取值上限,对于取值上限/下限的选取或限制应符合执行此时间参数的单机特性.
由数学模型的表达式来确定时序裕度的模型,即应考虑各个分段时间的上下限,规则是:
1)对于小于不等式,不等式左边的时间参数均以其取值上限计算,不等式右边的时间参数均以其取值下限计算.即若要求时间参数T小于Tl,则有:

2)对于大于不等式,不等式左边的时间参数均以其取值下限计算,不等式右边的时间参数均以其取值上限计算.即若要求时间参数T大于Th,则有:

3)对于等式,即若要求时间参数T在Tl~Th之间.左边为被分解项,其取值上限应不小于右边各分解项均按取值上限的计算结果:

其取值下限应不大于右边各分解项均按取值下限的计算结果:

3 时序过程的描述
由于卫星控制分系统工作流的上下文既有瞬时性(instantaneous)也有持续性(continuous)特点,因此控制分系统的系统级时序描述包括两个方面:基于时间点的工作流和基于时间区间的工作流.参照区间代数[7],定义基本的时序关系为:
工作流图用于表述控制系统各个工作主体(计算机、敏感器、执行机构、外系统、软件配置项)之间的工作流,以及这些工作流之间的同步或异步的交叉关系.

表1 基本时序关系Tab.1 Elementarytimingrelations
用Pij表示第i个工作主体的第j个动作,同时加入时间点(或事件、或条件)或时间执行区间.时间点用[tm,)表示,时间区间用[tm,tn]表示,条件用[CTp]表示,资源用[Y1,Y2,…]表示;多个时间(事件或条件)描述之间用/分隔.
例如:
工作流图是由表述这些带有时间约束的图形节点连接而成,如图1所示.
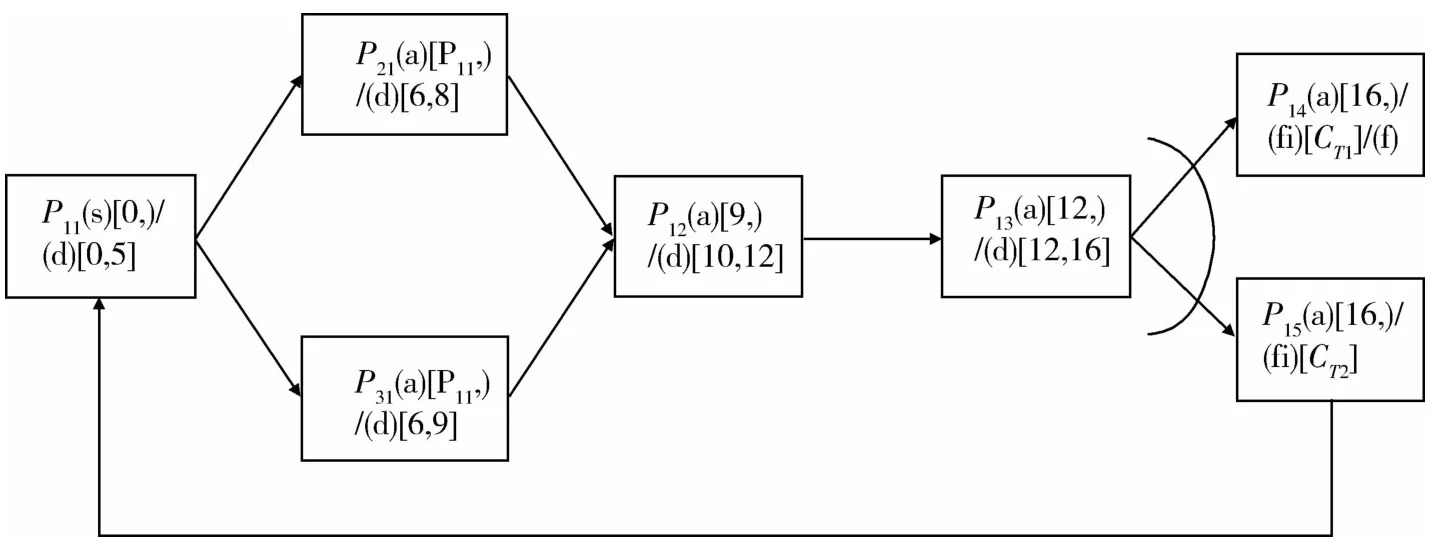
图1 工作流图Fig.1 Working flow chart
连接关系中,箭头代表了先后顺序关系;带有弧线的并列箭头所指的分支是条件判断分支;不带有弧线的并列箭头所指的分支是并行关系.前后方框中时间区间的差值,代表了所允许的时间裕量或响应时间或执行时延.
工作流图中动作的执行顺序是由工作流的执行控制结构决定的,这种执行时序约束没有明确的定义,但在执行过程中总要被满足,因此称为隐式时序约束.由各种基本时序关系符号所指明的时间点、时间区间、事件、条件、资源是显式时序约束.特别是对于时间要求,时间点与时间区间表达了动作持续时间约束、动作间的时间间隔约束以及允许的时延约束.
4 结 论
随着卫星控制系统集成度的提高和新功能的不断增加,系统时序的复杂度也越来越高,通过试错法设计时序参数效率过于低下且容易出错.本文提出了针对时序的数学建模分析方法和时序描述的工作流图方法,可用于卫星控制分系统的时序设计与分析.通过系统性的时序建模,可求解出时序过程中的所有时间参数,同时对系统测试具有指导意义.
[1]BURNS A,WEKKUBGSA J.Hard real time HOOD:a design method for hard real-time ada 9X systems[C]//Ada UK International Conference.Amsterdam:Ios Press,1992:201.
[2]BURNSA, WEKKUBGSA J,BAILEY C M,et al.The olympus attitude and orbital control system-a case study in hard real-time system design and implementation[C]//The 12thAda-Europe International Conference.Heidelbery:Springer-Verlag Berlin,1993:353.
[3]ERKKINEN T.Model style guidelines for flight code generation[R].AIAA 2005-6216,2005.
[4]TOTEL E,POLLE B,CHARMEAU M C.Modelling an autonomous spacecraft architecture[C]//DASIA.Nice:ESTEC,2001.
[5]FEILER P H,LEWIS B A,VESTAL S.The SAE architecture,analysis&DESIGN LANGUAGE(AADL)-a standard for engineering performance critical system[C]//The 2006 IEEE Conference on Computer Aided Control System Design.Washingto:IEEE Computer Society press,2006:1206-11.
[6]RUGINA A E,KANOUN K,KANICHE M.A System dependability modeling framework using AADL and GSPNS[M].Delemos R,Gacek C,Romanovsky A.Architecting Dependable System IV.Heidelberg:Springer-Verlag Berlin,2007:14-38.
[7]ALEFELD G,HERZBERGER J.Introduction to interval computations[M].New York:Academ ic Press,1983.

