卫星高精度相对姿态确定技术*

张春青，王淑一，陈 超

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

0 引 言

将星敏感器和陀螺的测量数据进行融合处理确定卫星姿态是高精度对地观测卫星通常采用的方法.大量研究表明，受空间热环境以及天区切换等因素影响，星敏感器测量数据中包含有低频误差项[1]，该误差表现为一定的周期特性且难以通过滤波方法加以消除，会对卫星姿态确定精度造成显著影响[2-5].星敏感器低频误差通常为十几个角秒的量级[1，5]，受该误差影响，采用星敏感器/陀螺组合定姿方法难以实现2.4″(3σ)的精度指标要求.考虑到陀螺特性为短期精度非常高，但输出为角度增量信息、缺少绝对基准，因此本文提出了一种基于陀螺测量信息的卫星高精度相对姿态确定方法.

文中对该方法的基本原理进行了介绍，并给出了理论分析、数学仿真以及物理仿真验证情况.

1 基于陀螺测量信息的卫星高精度相对姿态确定技术

方法基本原理为:利用陀螺信息确定一段时间内各时刻相对于起始时刻的相对姿态，起始时刻的绝对姿态加上陀螺确定的相对姿态即可确定各时刻的绝对姿态，其中起始时刻的绝对姿态精度由地面高精度标定等手段保证.

从以上方法描述可以看出，陀螺测量数据的精度直接决定了相对定姿方法的精度，而陀螺测量精度主要受其自身的漂移误差影响.陀螺漂移误差通常包括系统型和随机型两种，公式描述如下[6]:

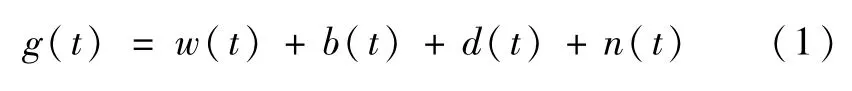
式中，g(t)为陀螺的测量输出，w(t)为沿陀螺输入轴的姿态角速率，b(t)为陀螺的常值漂移，d(t)为陀螺的相关漂移，n(t)为随机漂移，通常为白噪声.

在以上的陀螺漂移项中，相关漂移d(t)对姿态角速率测量的影响随时间增加呈指数衰减，在数以年月计的陀螺长时间应用中其影响可不予考虑.因此利用陀螺确定相对姿态的误差主要来源于陀螺测量误差中的随机漂移n(t)和陀螺常值漂移b(t)两项，其中陀螺常值漂移项可以利用星敏感器的测量数据进行估计.

综上分析，最终影响陀螺相对姿态确定精度的因素包括陀螺随机漂移和常值漂移估计残差两项.由这两项误差特性可知:随机漂移对姿态确定精度的影响与根号下时间呈正比关系;常值漂移估计残差对姿态确定精度的影响与时间呈正比关系，也即相对时间越长，姿态确定精度越差，因此满足精度指标要求的最长相对时间有所限制.

本节首先给出了基于星敏感器测量数据的陀螺常值漂移估计残差情况，在此基础上对基于陀螺信息进行相对姿态确定在不同相对时间内可以达到的精度情况进行了理论分析及数学仿真验证.

1.1 陀螺安装

仅基于陀螺信息的本体三轴姿态确定精度与陀螺安装构型相关，本文的分析以如下陀螺典型安装为例:以Xb轴为锥面中心，锥面半锥角为54°44′08″，均匀布置6个陀螺角速度的输入轴，安装示意图如图1所示.

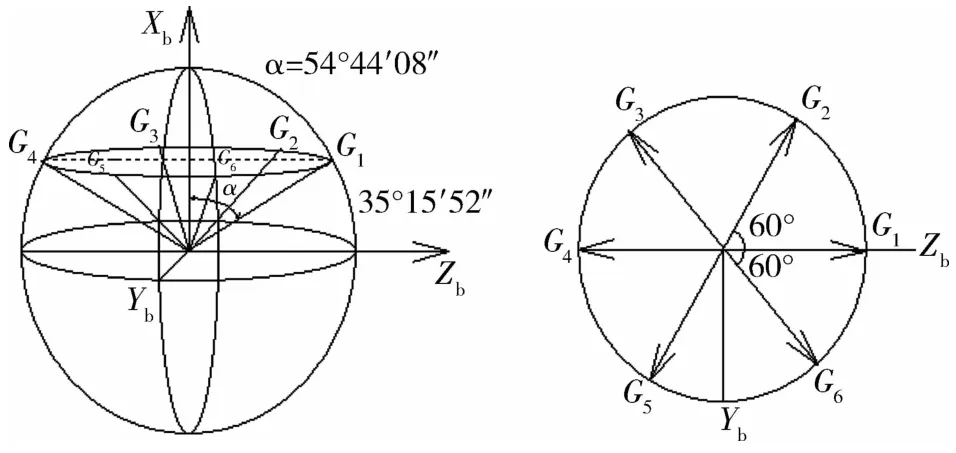
图1 陀螺安装示意图Fig.1 Installation of gyros

用符号G1～G6代表6个陀螺输入轴，则6个陀螺在本体坐标系O-XbYbZb安装矩阵为

1.2 陀螺常值漂移估计残差仿真分析

本节主要考察不同的星敏感器误差对陀螺常值漂移估计误差的影响情况.表1为仿真中部件的性能指标，仿真结果见图2.从仿真情况看，星敏感器估计陀螺常值漂移的精度受星敏感器自身精度影响较大.星敏感器无低频误差时，陀螺常值漂移的估计残差小于0.005(°)/h，考虑星敏感器低频误差的情况下，陀螺常值漂移的估计残差最大在0.01(°)/h左右.

表1 仿真中星敏感器/陀螺精度指标Tab.1 Star sensors/gyros errors in simulation

1.3 相对姿态确定精度理论分析结果

相对姿态确定由于仅利用陀螺的测量数据，因此基于不同陀螺组合确定的卫星本体三轴姿态精度情况有所不同.用符号代表选用的陀螺组合，则陀螺组安装矩阵为A=，其中，为如式(2)所示的陀螺安装向量.由以上陀螺安装可以求出从陀螺测量轴到卫星本体三轴的转换矩阵B=A-1，则Xb等效噪声与陀螺噪声的倍数为等效噪声与陀螺噪声的倍数为Zb等效噪声与陀螺噪声的倍数为其中代表矩阵B的第i行、第j列.

由上述关系可以计算得出:选1/3/5或2/4/6两组陀螺(三正交陀螺)，本体三轴等效噪声与单个陀螺噪声指标相同;选1/2/4陀螺(有陀螺相邻)，Yb轴等效噪声最大，为陀螺噪声指标的1.8倍;选用1/2/3陀螺(陀螺全部相邻)，Xb等效噪声最大，为陀螺噪声指标的3倍.

针对表1中三浮陀螺标称精度指标进行分析，常值漂移估计残差按0.01(°)/h(1.2节的分析结果)考虑.以选择三正交陀螺为例，相对时间100s后由陀螺随机漂移引起的姿态确定误差为1.98″(3σ)，由常值残差引起的姿态确定误差1″，综合两部分误差，100s相对姿态确定精度为2.98″(3σ).

按以上分析，在不同相对时间内相对姿态确定精度情况如表2所示.

从上述分析情况看，实现2.4″(3σ)的相对姿态确定精度指标，选用三正交陀螺，满足精度指标的最长相对时间为70s左右，如有一个陀螺故障，选用的3个陀螺中有2个相邻的情况，最长的相对时间只能为30s左右.

1.4 相对姿态确定精度数学仿真结果

选用表1所示的陀螺和星敏感器的标称指标进行数学仿真分析，精度统计结果如表3～4所示.表3是选用陀螺组1/3/5，相对姿态确定精度统计情况，表4是选用陀螺组1/2/4的相对定姿精度统计情况.

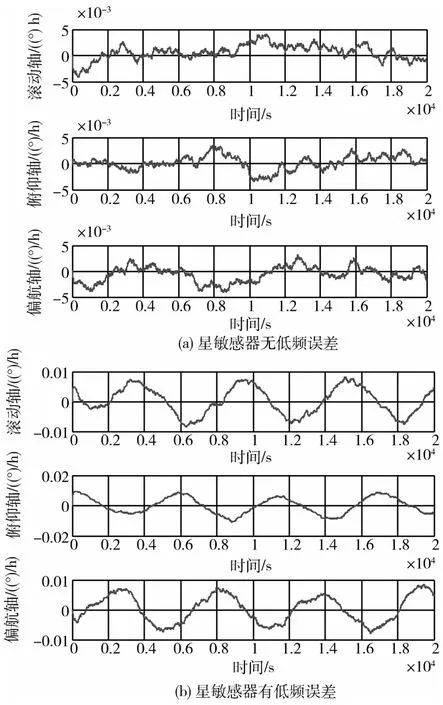
图2 三轴陀螺常值漂移估计误差(1/3/5陀螺)Fig.2 Gyros bias estimate errors(G1/G3/G5)

表2 相对姿态确定精度理论分析结果(3σ)Tab.2 Analysis results of relative attitude determination accuracy(3σ)

从数学仿真及精度统计情况看，对应于随机漂移精度为0.02(°)/h的陀螺，当选用三正交陀螺时在80s时相对姿态确定精度为2.39″(3σ)，可实现定姿精度指标，这一结果比1.2节分析的70s时间长了10s，分析原因主要是由于理论分析中陀螺常值残差以最大值0.01(°)/h考虑.当选用的陀螺为1/2/4时，可以看出Yb轴的精度最差，且在30s内实现精度指标约为2.33″(3σ)，与1.3节理论分析结果一致.

2 相对姿态确定技术物理仿真试验验证情况

为验证相对姿态确定2.4″(3σ)的精度指标，在北京控制工程研究所三轴气浮台上，针对所配置的三浮陀螺，进行了台体未浮时的静态试验和包括敏感器及执行机构的闭环动态物理仿真试验.

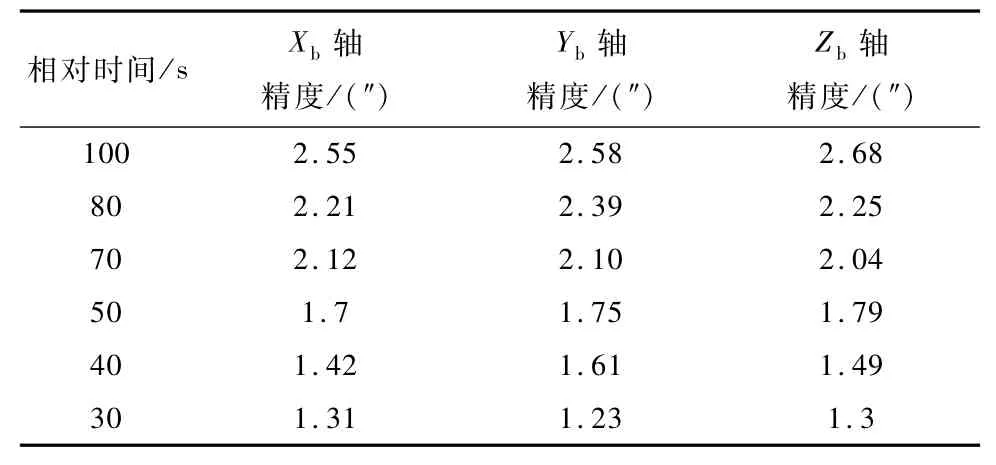
表3 陀螺相对姿态确定精度统计数学仿真结果 (1/3/5陀螺)(3σ)Tab.3 Simulationresultsofrelativeattitude determinationaccuracy (G1/G3/G5)(3σ)

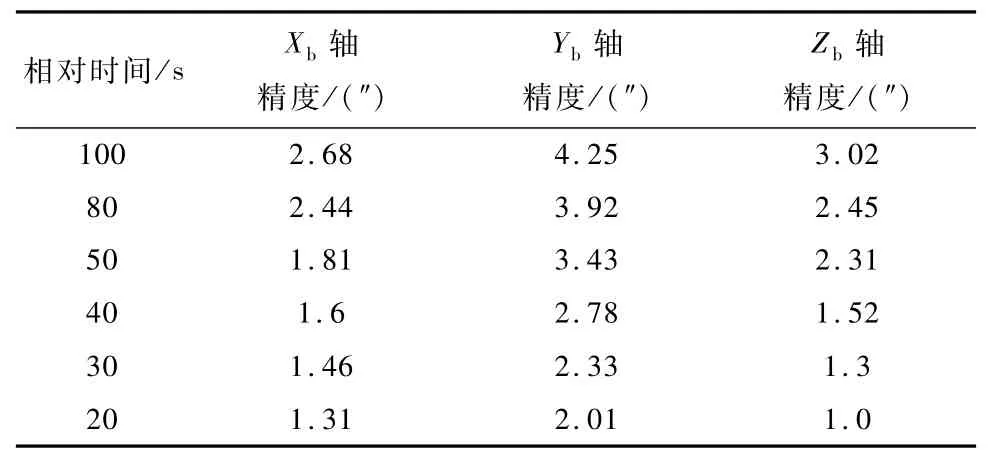
表4 陀螺相对姿态确定精度统计数学仿真结果 (1/2/4陀螺)(3σ)Tab.4 Simulation results of relative attitude determination accuracy(G1/G2/G4)(3σ)

静态测试主要对陀螺的性能指标进行测试.动态测试主要用来验证相对姿态确定精度.

2.1 静态测试数据分析结果

2.1.1 陀螺随机漂移统计

静态测试进行了约11h左右，陀螺输出数据如图3所示.陀螺输出数据如图3所示.按照部件精度统计方法对测试数据进行方差统计，具体为将测试数据按小时进行分组，对每组中数据进行100s平滑并统计方差，结果如表5所示.从统计结果看，3个陀螺的实测数据统计精度均优于标称精度(0.02(°)/h，3σ).

2.1.2 基于陀螺静态测试数据的相对姿态确定精度统计

静态测试可以认为真实姿态为零，利用减掉常值部分的陀螺输出数据统计出的相对姿态即为陀螺随机误差引起的相对姿态确定误差，同时考虑0.01(°)/h的陀螺估计残差，最终统计情况见表6.由于选用三正交陀螺时卫星三轴的等效噪声与单个陀螺相等，则实现2.4″(3σ)的相对姿态确定精度，选用三正交陀螺最长相对时间为100s左右.

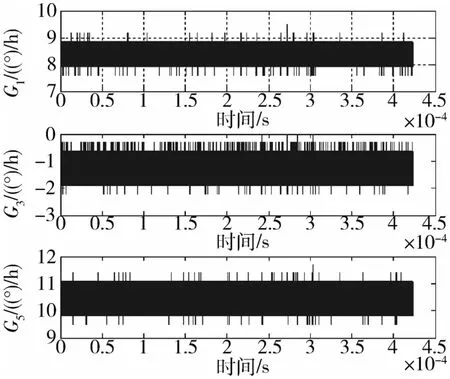
图3 气浮台静止时陀螺输出数据Fig.3 Gyros measurement data when the air-bearing table don’t float

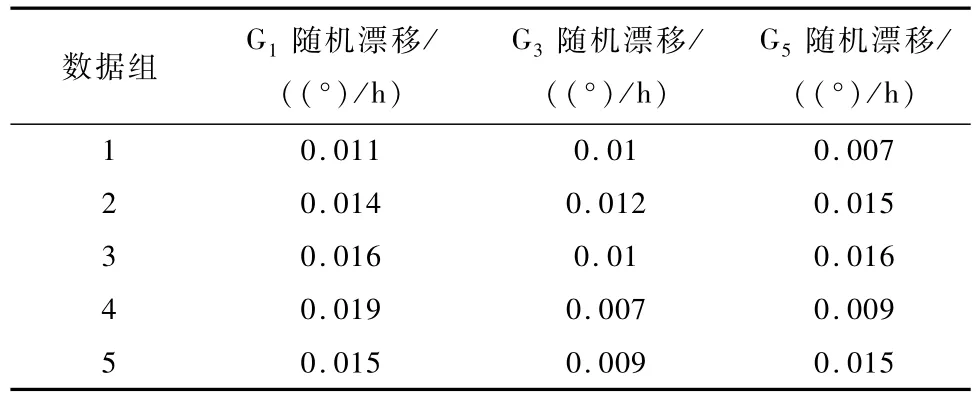
表5 三浮陀螺随机漂移统计(3σ)Tab.5 Random drift error of the three-floated gyro(3σ)

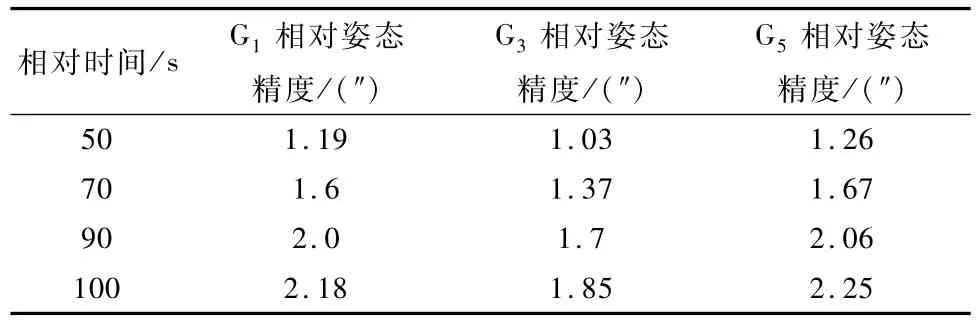
表6 陀螺实测数据相对姿态确定精度统计(3σ)Tab.6 Relative attitude determination accuracy based on gyro real measurement data(3σ)

2.2 动态测试数据分析结果

动态测试的敏感器包括3台正交安装的陀螺和两台自准直仪，陀螺测量台体三轴角速度、两台自准直仪测量台体三轴转角，执行机构采用动量轮.利用自准直仪测量，产生等效星敏感器测量数据，将星敏感器和陀螺的测量数据联合处理估计出陀螺常值漂移，将陀螺测出的三轴台体角速度减掉地速及估计出的常值漂移后的角速度数据作为相对姿态确定误差统计的数据来源.自准直仪测量数据作为精度比对基准.

2.2.1 自准直仪精度测试结果

由于采用自准直仪作为精度比对基准，因此试验首先对自准直仪的精度进行了测试.自准直仪精确安装后，在气浮台未浮时开启自准直仪并记录输出数据.由于台体未浮，自准直仪的输出数据即反应了自身的性能指标.

测试时间为12h左右，从测试结果看出:G1自准直仪的X向和G2自准直仪的精度较好，随机部分精度为0.4″(3σ)左右，趋势项漂移100s内为0.01″左右.如图4～6所示.图中的上图为自准直仪实测数据，下图为剔除趋势项变化的自准直仪噪声情况.因此将G1自准直仪的X向和G2自准直仪所测角度作为精度比对基准，对应台体的X和Z两个轴.

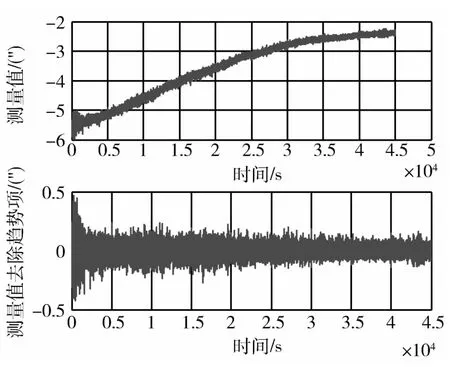
图4 G1自准直仪X向测量输出Fig.4 X-axismeasurement data of G1 autocollimator

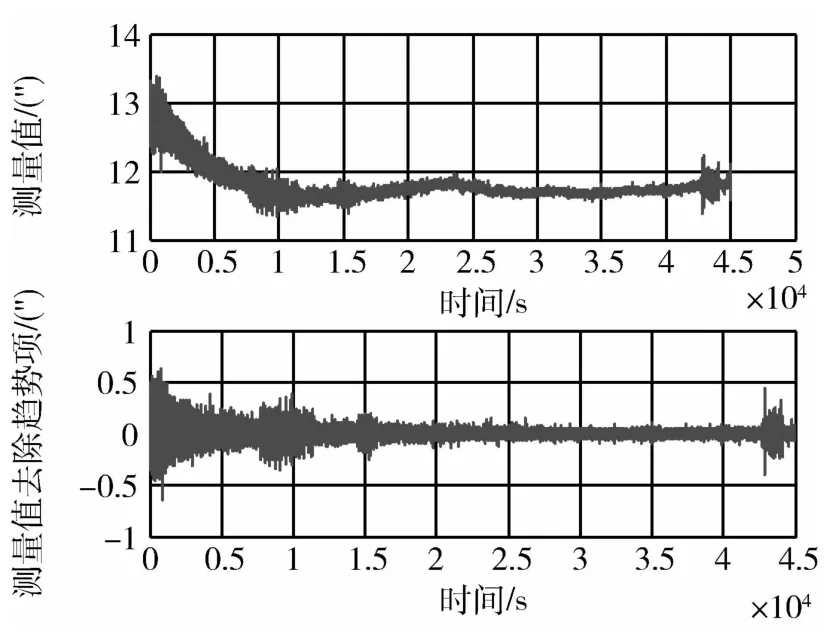
图5 G2自准直仪X向测量输出Fig.5 X-axis measurement data of G2 autocollimator

2.2.2 动态闭环测试数据处理结果

试验中自准直仪测量出的台体三轴姿态角变化如图7所示.将自准直仪测量数据输入到星敏感器测量模型，产生等效星敏感器测量数据，将星敏感器和陀螺的测量数据联合处理估计出陀螺的常值漂移，将陀螺测出的三轴台体角速度减掉地速及估计出的常值漂移后的角速度数据(图8)作为相对姿态确定误差统计的数据来源.

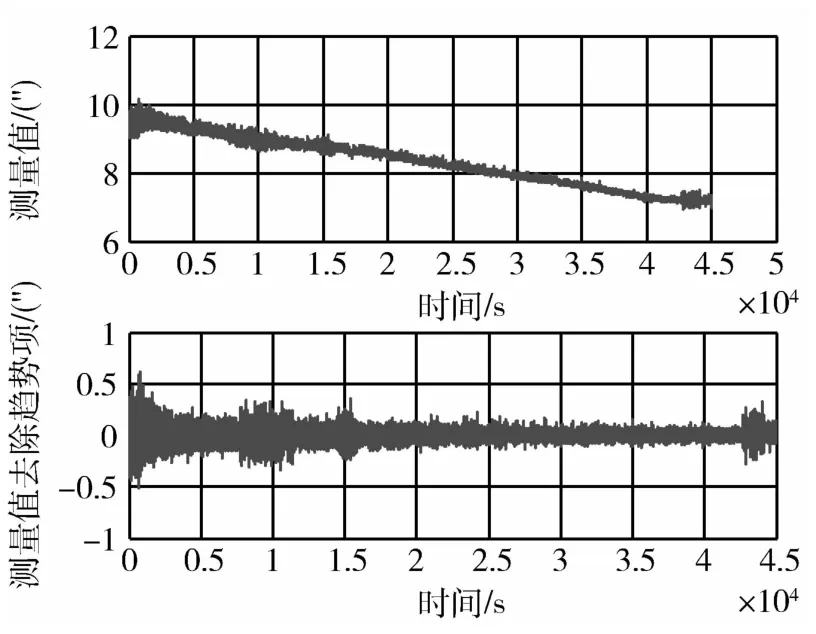
图6 G2自准直仪Y向测量输出Fig.6 Y-axis measurement data of G2 autocollimator

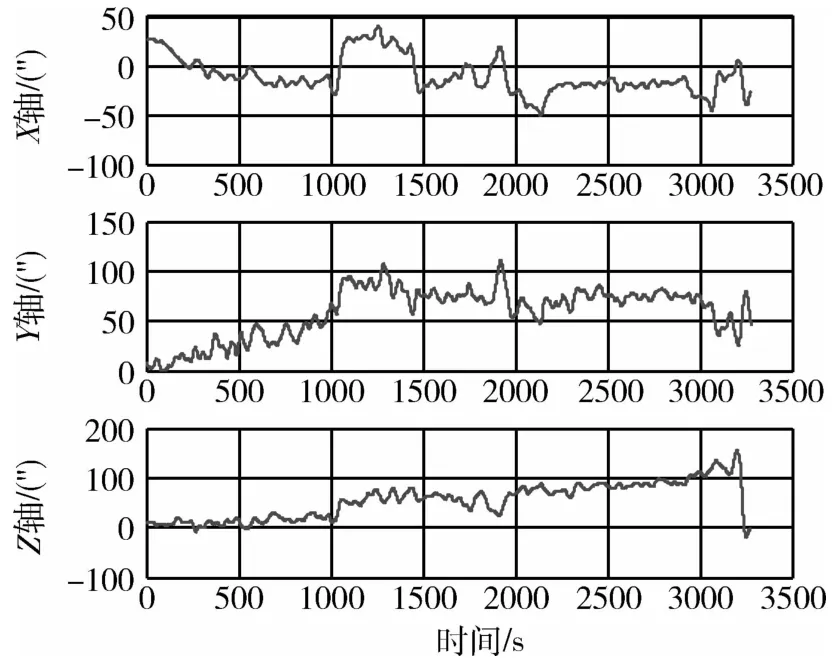
图7 自准直仪测出的台体三轴姿态角变化曲线Fig.7 Attitude angles of three-axis air-bearing table

图8 陀螺测出的台体三轴角速度变化曲线Fig.8 Attitude angular rates of three-axis air-bearing table

2.2.3 动态测试相对姿态确定误差统计

利用第2.2.2节中减掉常值漂移的陀螺测出台体的X轴和Z轴的测量数据统计相对姿态，与自准直仪的数据进行比对，可确定相对姿态确定误差.图9～10是相对时间100s时相对姿态确定误差曲线，不同相对时间统计的相对误差确定精度如表7所示.由于测试中3个陀螺为正交安装，因此精度统计结果对应于选用三正交陀螺的情况.

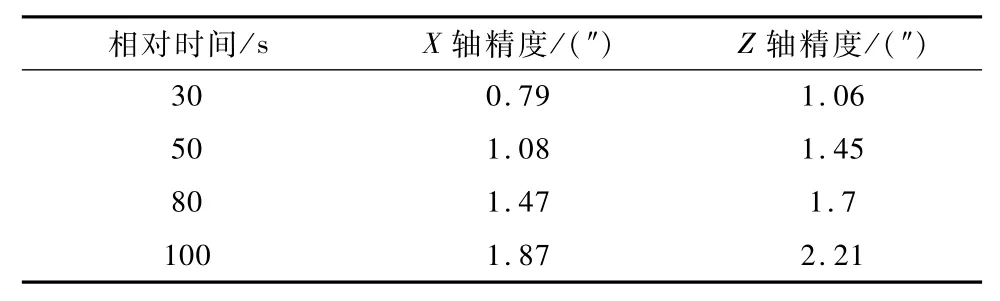
表7 陀螺实测数据相对姿态确定精度统计(3σ)Tab.7 Physical simulation results of relative attitude determination accuracy(3σ)

综合两轴的精度统计结果，同时考虑自准直仪的精度影响，三正交陀螺构型可以在100s内实现2.4″(3σ)的精度指标，这一结论与2.1节静态试验的分析结果基本吻合.

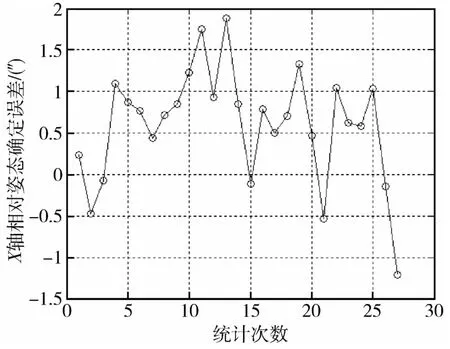
图9 100s相对姿态确定误差(台体X轴)Fig.9 Physical simulation results(100s，X axis)

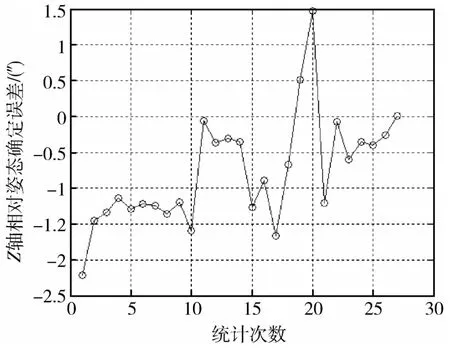
图10 100s相对姿态确定误差(台体Z轴)Fig.10 Physical simulation results(100s，Z axis)

3 结 论

从针对三浮陀螺标称指标进行的数学仿真及理论分析情况看:实现2.4″(3σ)的相对姿态确定精度指标，选用三正交陀螺，理论分析结果为最长相对时间70s左右，数学仿真结果为80s左右.物理仿真实测时陀螺的精度优于标称指标，因此用实测数据分析的相对姿态确定精度为:选用三正交陀螺最长相对时间为100s左右.综上，保守估计采用三浮陀螺应该可以在相对时间70s内实现2.4″(3σ)的相对姿态确定精度指标(陀螺选三正交构型).

综合以上分析，采用基于陀螺测量信息的相对姿态确定方法是在目前敏感器精度水平情况下实现角秒级姿态确定精度的一种可行方法.

[1]BLARRE L， OUAKNINE J， ODDOSM L.High accuracy Sodern star trackers:recent improvements proposed on SED36 and HYDRA star trackers[C]//AIAA Guidance， Navigation， and Control Conference and Exhibit.Colorado:AIAA，2006:21-24.

[2]HASHMALL J A， NATANSON G， GLICKMAN J， et al.Compensation for time-dependent star tracker thermal deformation on the AQUA spacecraft[R].NASA-20040171520，2004.

[3]JORGENSEN J L，DENVER T，BETTO M，et al.The PROBA satellite star tracker performance[J].Acta Astronautica， 2005， 56:153-159.

[4]JORGENSENP S， JORGENSEN J L， DENVER T， et al.In-flight quality and accuracy of attitude measurements from the CHAMP advanced stellar compass[J].Acta Astronautica， 2005， 56:181-186.

[5]IWATAT，HOSHINO H，YOSHIZAWA T，et al.Precision attitude determination for the advanced land observing satellite(ALOS):design， verification， and on-orbit calibration[C]//AIAA Guidance，Navigation and Control Conference and Exhibit.South Carolina:AIAA，2007:1-18.

[6]章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社，1998:217-219.