输入延迟未知的二阶对象的黄金分割控制*
胡 军
(北京控制工程研究所,北京100190)
0 引 言
按标称对象设计控制律,当存在输入延迟,或输入延迟与标称模型不符时,控制系统性能变差,甚至不稳定.因此,输入延迟未知对象的控制是控制理论和工程实践中的难题.
由于延迟环节在时间域是超越函数,在频率域是无穷阶的,带延迟环节的控制问题研究在理论上有很大难度;而在生产、测量、通信以及网络传输等实际工程中,延迟现象是普遍存在的,延迟系统的控制问题始终是控制工程师所关注的问题.因此有关延迟系统及其控制的研究,自控制理论成为一门学科以来始终持续地在进行,形成时域和频域两大研究方法[1-6],研究范围既含连续系统[1-4],也含离散系统[5-6].
输入延迟对象控制问题的研究,绝大部分针对的是确定性输入延迟,经典的结果如 Smith补偿器[7]和Dahlin算法[8],它们都是根据被控对象的精确数学模型进行设计,一旦对象参数变化,系统性能变差甚至不稳定.20世纪70年代以来发展的自校正控制[5-6],对被控对象参数进行在线估计,是解决输入延迟控制问题的可选方法,但对延迟参数变化的适应能力有限;文献[2]用有限阶传递函数近似延迟环节,在此基础上用已有方法设计控制器,闭环系统稳定性和性能须用原输入延迟对象验证.时域系统延迟问题的研究,主要方法是 Lyapunov-Krasovskii泛函方法和Razumikhin函数方法,它们是时滞系统稳定性分析的一般方法,目前发展到用Riccati方程或线性矩阵不等式并利用 Matlab工具箱的求解方法[3].将智能控制思想引入经典控制之中,也是改进输入延迟对象控制性能的途径[9].
研究未知输入延迟条件下二阶差分特征模型的控制律设计和稳定性问题.特征模型思想是1992年由吴宏鑫提出,经过20年来的理论工作,逐渐形成特征模型理论,并在实际中得到应用[10],目前该理论还在发展之中.一般情况下,特征模型用慢时变(或慢变)低阶差分方程描述,工程和应用研究中使用最广泛的是二阶差分特征模型[10].基于特征模型的控制律设计,需要结合吴宏鑫1981年提出并逐渐完善的全系数自适应控制理论[6],该理论揭示线性定常系统差分方程系数间的关系,并根据采样周期给出各系数的变化范围,解决了线性反馈控制时在线参数辨识的工程可行性问题.在满足增益约束条件下,黄金分割控制律保证了二阶差分特征模型参数未知情况下的反馈稳定性问题,解决了一般自适应控制在启动和过渡过程中参数未收敛所遇到的控制难点.目前二阶差分特征模型及其控制的研究还没有涉及到被控对象存在输入延迟未知的情况.
下面按照稳定、双积分、临界稳定、不稳定的分类,研究二阶差分特征模型[10]在未知输入延迟条件下控制器的设计问题,并给出结论.
1 两个经典控制理论成果在未知输入延迟应用中的启示
考虑二阶(特征)系统

目前在基于特征模型的控制器设计研究中,主要针对k0=0的情况.在实际工程和应用研究中,测量和控制总是或多或少地存在迟延,由于闭环控制系统采用测量输出反馈,研究闭环控制时,可将所有这些迟延等效加在输入上,因此实际对象通常k0>0.
对差分模型的控制,最经典的是最小方差控制[3].对象(1)在k0=0时的最小方差控制为

其中,α1、α2、β0分别是A1、A2、B0的估计,其主要的要求是.显然,最小方差控制将闭环极点都配置到原点,这是理论上不可超越的最好结果.不过,这一理论自提出起,几乎没有成功的应用.本文从应对输入迟延的角度探讨这个问题,因为对延迟的鲁棒性也是闭环系统鲁棒性的一个重要方面.
对k0=0情况下的二阶特征模型(1),参数鲁棒性最好的是黄金分割控制律[1],
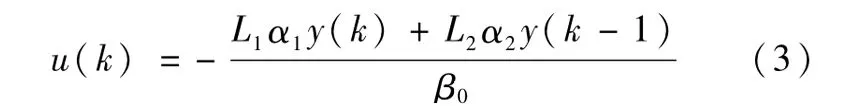
式中,L1=0.382,L2=0.618.
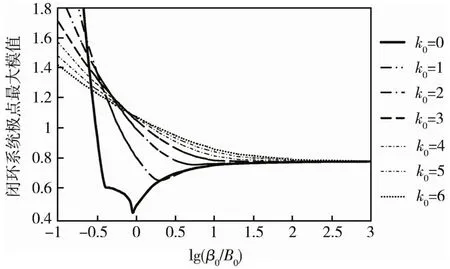
图1 β0/B0和k0的不同取值下,闭环系统极点最大模值(黄金分割控制律)Fig.1 The maximum modulus of the closed-loop system poles with respect toβ0/B0 and k0(golden-section control law)
从图1可以看出:①无输入延迟条件下,即k0=0时,当β0/B0<0.31时,闭环系统不稳定.这已经不满足黄金分割控制要求β0/B0大于0.5的假设条件,但实际工程和应用研究中,参数估计并不一定能保证这一条件;②β0=B0条件下,k0=1时闭环系统稳定,k0=2时闭环系统仍稳定,但很接近临界状态,k0≥3时,闭环系统不稳定;③对任意k0,稳定性随β0/B0增大而变好,当β0/B0≥2时,k0=0,1,…,6,分别对应2~8阶闭环系统,极点最大模值小于1,闭环系统均稳定.因为开环对象是稳定的,β0/B0增大,反馈增益B0/β0减小,闭环极点最大模值趋向于开环稳定极点模值.图1是理论研究结果,实际上β0/B0的数值受到参数范围限制,不超过B0max/B0min.
从上述分析可知,对稳定对象,其稳定性和鲁棒性与输入系数B0的估计值β0密切相关,而对迟延步数k0的鲁棒性指标,随β0/B0增大而变好,参数完全精确估计,不能保证对k0的鲁棒性也好.在工程应用中,如果系统最大增益未知,或大范围变化,或在控制启动阶段,β0很难正确估计.β0估计困难和β0/B0数值不够大,制约了黄金分割控制律(3)对输入延迟的适应能力.图2给出对应的脉冲响应曲线.从图中可以看出,k0=0,1,2时,闭环系统稳定,但稳定余量和性能随k0增大而变差,k0=3时闭环系统不稳定.
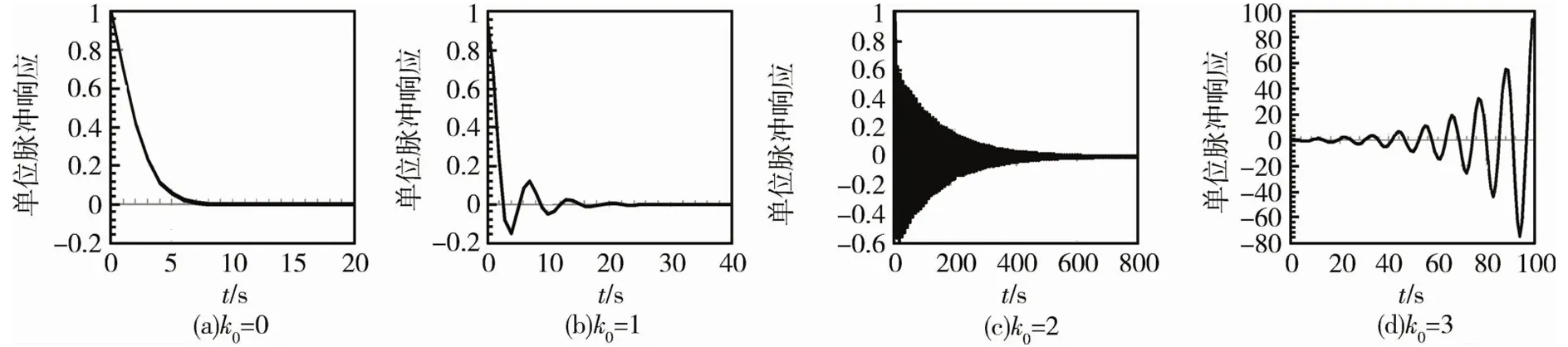
图2 参数无差情况下,黄金分割控制律对k0的鲁棒性仿真(A1=1.5,A2=-0.6,B0=0.1)Fig.2 The robustness of golden-section control law with respect to k0 with completely matching parameters(A1=1.5,A2=-0.6,B0=0.1)
对不同的A1、A2、B0,控制律适应k0的具体数据有差异,但规律是类似的.图3给出A1=1.85,A2=-0.95,B0=0.1对应的脉冲响应曲线.从图中可以看出,k0=0,1时,闭环系统稳定,k0=2时闭环系统不稳定.

图3 参数无差情况下,黄金分割控制律对k0的适应性仿真(A1=1.85,A2=-0.95,B0=0.1)Fig.3 The adaptability of golden-section control law with respect to k0 with completely matching parameters(A1=1.85,A2=-0.95,B0=0.1)
综上,最小方差控制应对延迟能力差,因其对标称模型完全补偿,标称之外的情况完全没有考虑;黄金分割控制应对延迟的能力不够,因其参数设计完全针对二阶系统,有未知延迟情况下,闭环系统变为高阶系统,稳定性迅速变差.延迟环节的频率特性幅值恒为1,相位滞后随频率增大而成比例增大,输入有延迟的系统相对输入无延迟的系统,其增益裕度降低[4].因此对未知输入延迟被控对象,采用小增益反馈控制,是解决未知输入延迟的可行方法.
2 黄金分割控制律用于开环稳定对象的研究
本文称式(3)为原型黄金分割控制律,在实际工程和应用研究中,根据实际情况,它产生一些变种.对实际工程中最常见的开环稳定对象,一种改进的黄金分割控制律如下[1]:
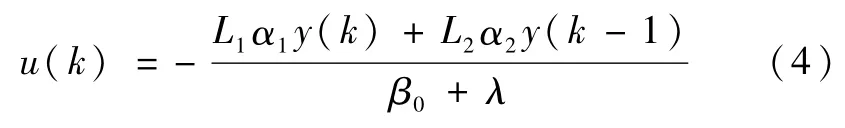
一些应用将λ称为“防零参数”[1],实际上β0∈黄金分割控制律中无须对β0进行防零,下面将看到,对开环稳定对象,从应对输入迟延角度设计控制器时,λ有其特殊作用.
本文称式(4)为λ型黄金分割控制律.采用式(4),上一节的变为,通常1,一般取大于2B0max的λ,在范围内,无论β0如何,都满足黄金分割使用条件.同时λ型黄金分割控制相对原型黄金分割控制,反馈增益变为原来的因此从机理上有助于未知输入延迟系统的稳定.
从图4可以看出,无论β0如何取值,k0=0,1,…,6,分别对应2~8阶闭环系统,极点最大模值均小于1,闭环系统均稳定.随β0/B0增大,反馈增益B0/(β0+λ)减小,闭环极点最大模值趋向于开环稳定极点模值.
对式(4)和式(1)组成的闭环系统,特征方程为
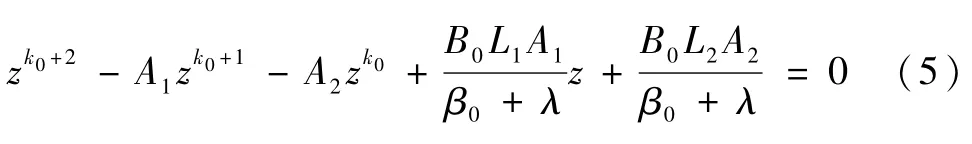

图4 闭环系统极点最大模值随β0/B0和k0的变化(λ型黄金分割控制律,λ=1)Fig.4 Themaximum modulus of the closed-loop system poles with respect toβ0/B0 and k0(λ type golden-section control law withλ=1)
随β0/B0增大,闭环极点最大模值趋向于开环稳定系统z2-A1z-A2=0确定的极点模值.实际上,当λ≥max(2B0max,1)时,闭环极点相对β0/B0的变化很不敏感,闭环极点对估值参数、增益以及输入延迟的鲁棒性都很好,稳定对象的k0可以远大于6.
图6给出参数估计未收敛条件下,原型与λ型黄金分割控制律对开环稳定对象的控制情况.对原型黄金分割控制律而言,各闭环系统随β0/B0的增大,依次从不稳定进入稳定.当β0=B0时,仅能稳定k0=0和k0=1;而采用λ型黄金分割控制律,则对参数范围内的β0和k0=0,1,…,6,闭环系统均是稳定的.从图中闭环极点最大模值看,λ型黄金分割控制律对应的性能也是能保证的.
黄金分割控制律对二阶开环稳定系统(1)的输入延迟适应能力与开环稳定余量和β0/B0有关.开环稳定余量小的,闭环系统适应延迟的能力也小;反之亦然.
考察单输入单输出连续被控对象

图5 参数无差情况下,λ型黄金分割控制律对k0的适应性仿真Fig.5 The adaptability of λ type golden-section control law to k0 with completely matching parameters

图6 β0/B0和k0的不同取值下,闭环系统极点最大模值(原型与λ型黄金分割控制律性能比较)Fig.6 The maximum modulus of the closed-loop system poles with respect toβ0/B0 and k0(comparison between prototype and λ type golden-section control laws)

其中,τ是未知的输入延迟,要求将对象从零初始状态控制到稳态输出值为10,控制输入幅值不大于30000.
采用式(1),取k0=0,即用无输入延迟的二阶特征模型作为控制器设计用模型,控制周期0.01s,按λ型黄金分割和标准全系数自适应控制方法设计控制器分别取λ=0(退化为原型黄金分割控制)和λ=1,图7(a)、图7(b)分别给出两种情况在τ=0,6s,12s,18s,24s,36s,48s情况下的仿真曲线.从图中可以看出,λ=1对输入延迟的稳定性和性能鲁棒性远优于λ=0的情况.如果没有输入限幅,λ=0对较大的τ,会造成闭环系统不稳定.
3 黄金分割控制律用于非稳定对象的研究
3.1 双积分环节对象
双积分环节对象,二阶特征模型为


图7 两种情况的阶跃响应Fig.7 The step responses of two types
分别用原型、λ型黄金分割控制律(3)、(4)与(8)组成闭环系统.对闭环极点最大模值的研究结果见图8~9,其中λ=0对应原型.

图8 双积分对象的原型、λ型黄金分割控制律对应的闭环系统极点最大模值Fig.8 The maximum modulus of the closed-loop system poles for the prototype and λ type golden-section control laws of a two-integrator plant
从图8中可以看出,对原型黄金分割控制,参数估计完全收敛(β0/B0=1),无延迟、一步延迟、二步延迟系统稳定,三步及多步延迟系统不稳定;当β0/B0增大时,最多能做到三步延迟系统稳定,再大的延迟系统不稳定.对λ型黄金分割控制,取λ=1,能做到最多四步延迟系统稳定,再大的延迟系统不稳定.
图9比较了λ分别取0、0.2、1时的闭环极点最大模值,模值小于1为闭环系统稳定,模值越小代表收敛越快.从图中可以看到,对于双积分环节这类开环稳定裕度小的对象:①λ=0,即原型黄金分割控制,对k0=0,1,相对λ型黄金分割控制,性能更好;②λ型黄金分割控制,λ=0.2,对k0=0,1,2,3,相比λ=1,性能更好;③λ型黄金分割控制,λ=0.2,对k0=2,3,4,相对原型黄金分割控制,性能更好;④λ型黄金分割控制,λ=1,能稳定的范围最大,对k0=4,对比其他两种情况,性能更好;⑤k0=5,各种方法,闭环系统均不稳定.
3.2 震荡环节对象

震荡环节对象的特征模型为其中,T为开环系统震荡周期,Δt为采样周期,对象(8)的开环极点为位于单位圆上的两共轭复数.

图9 双积分对象的原型、λ型黄金分割控制律对应的闭环系统极点最大模值(k0=0,1,2,3,4,5)Fig.9 The maximum modulus of the closed-loop system poles for prototype and λ type golden-section control law of a two-integrator plant(0-,1-,2-,3-,4-or 5-step delay)

图10 震荡环节对象的原型、λ型黄金分割控制律对应的闭环系统极点最大模值(k0=0,1,2,3,4,5)Fig.10 The maximum modulus of the closed-loop system poles for prototype and type golden-section λ control law of oscillation plant(0-,1-,2-,3-,4-or 5-step delay)
3.3 不稳定对象
开环不稳定对象的控制,其闭环稳定性对增益估计有很强的条件,黄金分割控制要求β0/B0在0.5和2之间.
考察二阶不稳定对象特征模型,

其开环极点z1=1.0463,z2=1.0029.
对不稳定对象(10),分别用原型和λ型黄金分割控制律进行分析计算,结果见图11.
从图11可以看出,原型和λ型黄金分割控制律,在适当参数下,最大闭环可稳定对象(9)的延迟步数k0=2,λ型黄金分割控制律对增益的鲁棒性更好一些,而原型黄金分割控制律在稳定的前提下性能更好一些.
4 结 论
对二阶开环稳定对象,原型黄金分割控制律对输入延迟的适应能力与β0/B0具体数值相关,采用λ型黄金分割控制律能够适应大范围输入延迟,对增益变化和输入时延鲁棒性好.
对二阶开环非稳定对象,λ型黄金分割控制律对增益和输入延迟的鲁棒性更好一些,而原型黄金分割控制律在闭环稳定和较小的输入延迟条件下,闭环性能更好一些.对非稳定对象,在设计控制律时,应根据先验知识,综合考虑稳定性和系统性能指标要求,优选λ(≥0),在确保稳定条件下寻求性能最优.
[1]秦元勋,刘永清,王联.带有时滞的动力系统的运动稳定性[M].2版.北京:科学出版社,1989:93-204.
[2]项国波.时滞系统优化控制[M].北京:中国电力出版社,2009:43-103.
[3]吴敏,何勇.时滞系统鲁棒控制:自由权矩阵方法[M].北京:科学出版社,2007:28-199.
[4]吴麒,王诗宓,杜继宏,等.自动控制原理[M].2版.北京:清华大学出版社,2006:184-185,256-258.
[5]ASTROM K J,WITTENMARK B.On self tuning regulator[J].Automatica, 1973, 9:185-199.
[6]吴宏鑫.全系数自适应控制理论及其应用[M].北京:国防工业出版社,1990:10-332.
[7]SMITH O J M.Close control of loops with dead time[J].Chemical Engineering Progress Trans, 1957,53(5):217-219.
[8]DAHLIN E B.Designing and tuning digital controllers[J].Instrument&Control System, 1968,41(7):77.
[9]崔坤林,张翼飞.时滞系统的经典控制与智能控制[J].微计算机信息,2004,20(6):25-26.CUIK L,ZHANG Y F.Classical control and intelligent control for the time delay system[J].Control&Automation,2004,20(6):25-26.
[10]吴宏鑫,胡军,解永春.基于特征模型的智能自适应控制[M].北京:中国科学技术出版社,2009:45-154.

