《空间几何体的三视图》复习课课堂实录

赵书鹏 张延敏 慕波

创设情境，激发兴趣

师：（用多媒体显示图片）今天我们来共同复习空间几何体的三视图，大家看老师准备的PPT上的这首诗，我们来一起读一下。

生（齐读）：横看成岭侧成峰，远近高低各不同，不识庐山真面目，只缘身在此山中。

师：这是苏轼的一首《题西林壁》，结合图片大家看前两句是否给我们一些启示呢？

生1：诗中蕴含的就是三视图中的正视图和侧视图的思想。

师：非常好，今天我们就来认真研究一下三视图。

设计意图：以上是课题引入，应用计算机辅助教学，通过形象直观的图片和文字，激发学生学习数学的兴趣，提高他们的积极性，更重要的是引导他们用数学思维解决生活中的问题。

知识复习，温故知新

师：请同学们回忆一下三视图包含哪几部分？

生2：三视图包含：正视图，侧视图，俯视图。

师：好，那么以长方体为例，请说明它的正视图、侧视图、俯视图是如何得到的。

生3：光线从几何体的前面向后面正投影，得到的投影图叫该几何体的正视图；光线从几何体的左面向右面正投影，得到的投影图叫该几何体的侧视图；光线从几何体的上面向下面正投影，得到的投影图叫该几何体的俯视图。

师：非常全面。那么如果给出几何体直观图，如何画出它的三视图呢？

生4：先观察分析物体的基本形体组成及其形状大小，位置关系，再确定正视方向并画出正视图，最后根据“三等关系”（长对正，高平齐，宽相等）画出侧视图和俯视图，

师：还有补充吗？

生5：画完后还要对照（直观图和三视图）检查。同时注意虚、实线（分界线和可见轮廓线用实线画出，不可见轮廓线用虚线画出）。

设计意图：必备的基础知识复习是习题课的基础，尤其是三种视图定义的复习，通过多媒体技术，由几何体通过投射线进而形成视图，把立体到平面的转换过程很自然地呈现在学生面前，化难为简，易于接受。

问题引入，例题讲解

设计意图：三视图的问题在近几年的高考中以选择题和填空题为主，大体分三个类型：①已知直观图，找三视图中一个（选择题），见类型一；②已知三视图，还原直观图（选择题），见类型二；③已知三视图，求直观图的体积和表面积（填空题），见类型三。

类型一：已知直观图画三视图

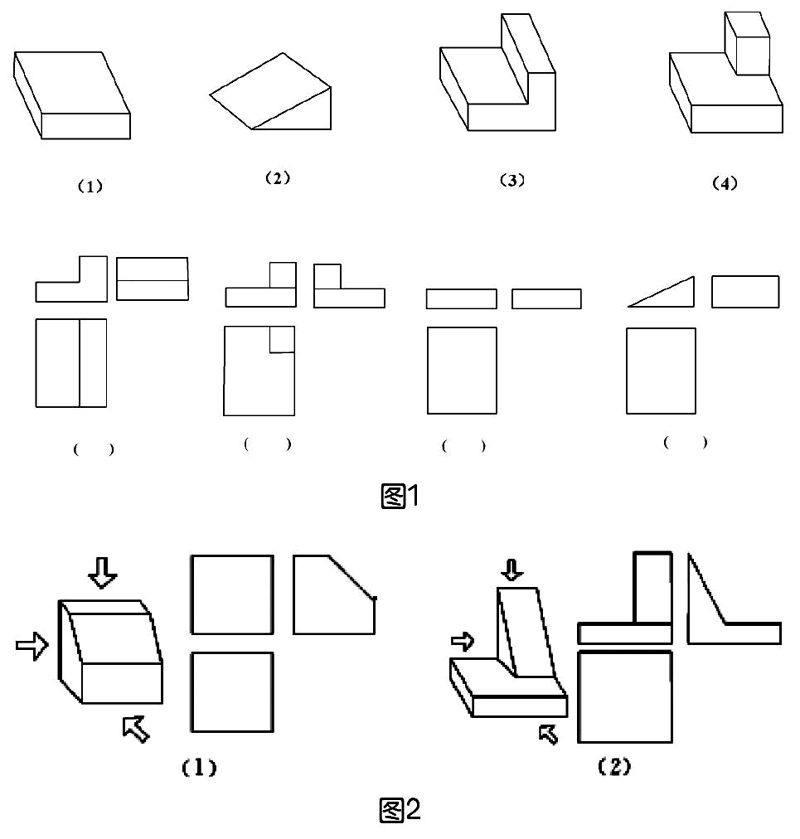
教师：例1，找出与下列几何体对应的三视图（如图1），并在对应的三视图下面的括号中填上数码。

生6：分别是3，4，1，2。

师：非常好。例2，添线补全下列三视图（如上页图2）。

（本题学生口答很流利，解答时注意虚、实线，分界线和可见轮廓线用实线画出，不可见轮廓线用虚线画出。）

设计意图：培养学生识图辨图能力。

师：例3，画出下列几何体的三视图，大家把视图画在白纸上，画完的同学交给老师，老师把它投影出来共同欣赏。

教师巡视把学生画的三视图用电子投影仪投出来（如图3），并共同分析、讲授。

设计意图：重在考查学生的观察能力和表述能力。

类型一设计意图：本例是由立体到平面的过程，题中4个图由易到难，让学生自己去画，教师不参与，完全放手给学生，引导学生按照三视图的画法一步步去画，在这个过程中，培养学生独立自主的精神，科学严谨的学习态度。

类型二：已知三视图还原直观图

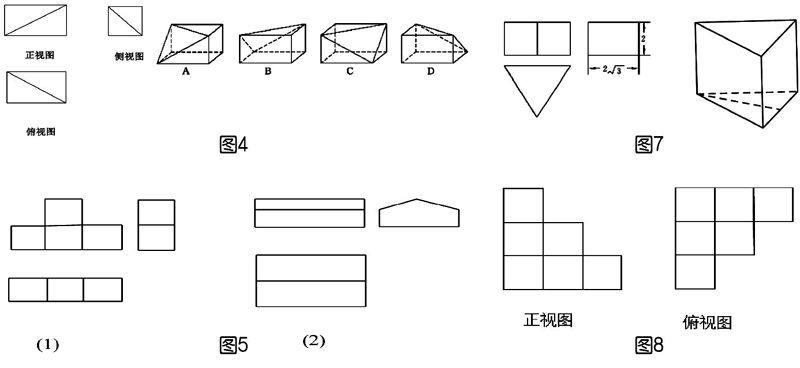
师：例4，选出此简单几何体三视图对应的实物图（如图4）。

（本题学生口答，很流利）

师：完全正确。好，看例5，根据三视图想象物体原形（如图5），并画出物体的直观图。画好后我们来共同投影欣赏。

本题学生动手画图，教师把学生画的结果投影出来（如图6），注意得到几何体的虚实线问题。

类型二设计意图：此类型是由平面到立体的过程，笔者安排了2个例题，尤其是例5，让学生明确不仅要重视正视图，还要兼顾侧视图和俯视图，在这个环节中学生要不断去想、去画，去动手、去修正，只有这样才能逐步实现由眼中有图到心中有图，从而培养学生手眼心的协调能力。

类型三：已知三视图，求直观图形体积表面积

师：例6，一个正三棱柱（底面是正三角形，高等于侧棱长）的三视图如图7所示，求这个正三棱柱的表面积。

（本题难度不大，学生计算后会很快得出结果，给学生一些时间让他们充分消化。）

生7：表面积是 。

师：非常好，下面大家看例6，用单位正方体块搭一个几何体，使它的正视图和俯视图如图8所示，它的体积最大值，最小值。

（让学生小组讨论后由各小组代表发表见解）

第4小组代表：我们组认为最大值是14，最小值是9。我们发现本题的几何体可以用一个3×3×3的魔方转化，由正视图发现第2列第1组，第3列1、2组必须没有，则去掉，剩下的部分满足正视图；再看俯视图，第2列第3组，第3列2、3组必须没有，则去掉，此时剩下的正方体就是本题的最大值。至于最小值，我们发现取最大值时俯视图中第1列的3组正方体中只要保留一组3个正方体即可满足2个视图，另2组保留1个正方体。同理，俯视图第2列保留1组2个正方体另一组保留1个即可，俯视图第3列保持不变，则得到最小值9。

第2小组代表：我们组也认为最大值是14，最小值是9。但我们的方法和第4小组恰恰相反，我们先由俯视图出发，布置出6个正方体，再观察正视图，发现第1列高度是3，第2列高度是2，第3列高度是1，则在俯视图的第1列3个位置都放2个正方体，第2列2个位置都放1个正方体，第3列不再放，则得到最大值14；构造最小值时，还是由俯视图出发，布置出6个正方体，再观察正视图，发现第1列高度是3，第2列高度是2，第3列高度是1，则在俯视图的第1列3个位置只选1个位置放2个正方体，其余2个位置不变，第2列2个位置选1个位置放1个正方体，另1个位置不动，第3列不再放，则最小值9就得到了。

师：非常好，大家说得很精彩，说明你们的讨论很有效。我们再请一位同学简练说明一下此几何体两种最值的构成方式。

生8：由2个视图可知左起第一列前中后三个位置都有正方体，每个位置最多3个，最少1个，但必须有一个位置放3个，第二列前后2个位置都有正方体，最多2个，最少1个，但必须有一个位置放2个，第三列有且只有1个（如图9）。

师：这位同学说得非常好，他把本题最难的地方用精炼的语言表达得非常清楚、明白。大家掌声鼓励一下。

类型三设计意图：课堂进行到此学生开始进入精力疲劳期，此时安排1个趣味性很强的问题，意在重新激发学生的学习兴趣，让学生通过自主阅读，小组讨论，得出结果，给出方案。对于提高学生周密思维能力，协调能力，同伴互助能力是有好处的。另外，笔者认为课堂是学生的，应该让他们动起来，当他们真正动起来的时候，通过小组合作，思想交流，进而得出自己的结论。不但能提高课堂效率，而且会让学生很有成就感。

回顾反思 课堂小结

师：这节课我们就共同研究到这里。下面请同学总结一下我们今天讲了哪些知识。

生9：今天我们主要学习了三个类型有三视图问题，分别是：①已知立体图，找三视图中一个；②已知三视图，还原立体图；③已知三视图，求立体图的体积、表面积。

师：非常好，希望我们大家在此基础上加强训练和总结，好让自己不断进步。

本节课作为空间几何体的三视图复习课，合理利用了信息技术来辅助教学，最大的特点是形象、直观，学生更容易接受新知，通过这样的信息技术的辅助，使学生更快乐，课堂更精彩。