全微分方法在动量定理的适应性研究

张进福 李建宽

（河北建筑工程学院 数理系 河北 张家口075000）

0 引 言

众所周知，随着国家“十一五”计划的逐步实施，一大批优秀高等教育的教材也应运而生.由北京邮电大学出版的、赵近芳和王登龙教授编写的《大学物理学》就是其中的一本.虽然这样的好教材在一定程度上，体现了“高、宽、新、活、宜”的教材写作风格，更加适应当前教学改革的要求.但是，在追求反应新科技发展的过程中，难免所新选的内容与原版教材中的原理部分有些不融洽、不适应，这种不适应可能来自于教材作者和教材的讲授者之间；也可能来自于教材本身的内容衔接有些不足.

为了解决以上的问题，通过认真思考和比较，我们在力学部分引入高等数学的全微分的思想，构建二元函数全微分下的动量定理的对称公式.以下我们围绕这个问题进行讨论.

1 关于适应性和二元函数的全微分

适应性是生物与环境表现相适应的现象，经典的解释就是达尔文的适者生存，不适者被淘汰.也就是说生物在长时间地与环境的应激能力的不断固化下形成的一种和环境相适应的特征，但此回答同时不应忽略环境的主动作用.

在学习的过程中，适应性不仅仅是指学习者和学习环境相适应，也应该包括教材本身主动地不断改编以适应于学生更好地学习.

对二元函数f（x，y）来说，如果在给定的单联通区域，它的两个对x和y偏导数存在，全微分的表达无非是把对其两个自变量x和y分别求的那两个一阶偏导数求出，然后写成如下形式即可.

更一般的讨论是：根据二元函数的一阶微分方程P（x，y）dx＋Q（x，y）dy＝0，方程的左端恰好表达的是一个二元函数u（x，y）的全微分.即：du（x，y）＝P（x，y）dx＋Q（x，y）dy.

根据对一个二元函数的全微分的要求，我们知道：存在一个开区域G，而且，是单联通区域，在这个区域内，P（x，y），Q（x，y）正好就是这个二元函数u（x，y）对x和y的一阶偏导数.

从以上的讨论，可以看出：

1）这两个一阶偏导数，具有在G内连续的的特征；

2）由于u（x，y）仅是x和y的二元函数，再由于两个偏导数就是函数对于x和y而进行的数学运算，所以，相对具于变量x和y来说，全微分运算具有数学运算的完备性特征.

2 动量定理的相关讨论和做法

2.1 利用动量定理的例题

从赵近芳，王登龙教授主编的《大学物理学》的第二章第六个例题中，可以看到如下的文字“如图2.13所示，一辆装矿砂的车厢以v＝4m／s的速率从漏斗下通过，每秒落入车厢的矿砂为k＝200kg／s，如欲使车厢保持速率不变，须施与车厢多大的牵引力（忽略车厢与地面的摩擦）.”

在该例题的解题过程中，书中先假设t时刻已落入车厢的矿砂质量为m，经过dt后又有dm＝kdt的矿砂落入车厢，这里取m和dm为研究对象，则系统沿x方向的动量定理为

在这本书的第二章第三小节第一部分内容里，写下了这样的表述：

牛顿在研究碰撞过程中，所建立起来的牛顿第二定律的形式是：

只是因为在先前（高中阶段物理课程）对牛顿力学的教学中，质点质量m是一个常数.→F＝m→a在形式上与（2.10）等价，由近代物理的观点看来，式（2.10）具有更广泛的适应性.

而动量定理的内容是：在给定的时间内，外力作用在质点上的冲量，等于质点在此时间内动量的增量.

问题很明显了，就是在本例题前面的章节里并没有与li的动量定理例题中使用的有关动量定理的表达式.

我们以为，在此例题中所要使用的动量这一函数，已经超出了一元函数的范畴，理应使用二元函数的相关计算方法.

2.2 动量定理的进一步讨论

我们知道，牛顿本人将他的研究成果写成（2.10）式时，并没有意识到m不是常数，而是认为“mv”是一个独立的物理量.也就是说，mv是由质量和速度联合确定的.而不是由m和v之中的某一个单独能够确定的物理量.

这里，我们借用高等数学里有关全微分的公式，把上式进一步写成如下形式：

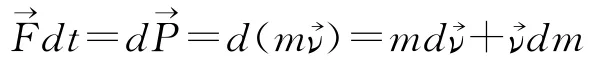
3 结 论

针对应用动量定理的时候，可能会遇到变质量和质量不变的情形，而当这样的问题经常地出现在的物理教学实践中的时候，我们有必要借助高等数学的相关知识，调整原来动量理论部分，以适应于各种动量改变的情形.

在上述例题或是不变质量质点系计算其动量变化的题目中，可以直接使用公式.

在近两年担负计算机专业和管理专业大学物理课程的教学中，收效不错.

故此，我们在高等数学中，关于全微分数学运算的完备形式引导下，完成了关于质点系变质量体系和质量相对不变体系的动量定理的完备形式的讨论.

［1］赵近芳，王登龙.《大学物理学》［M］.北京邮电大学出版社，2011，（12）35～39

［2］何挺秀，胡向东.冻土帷幕平均温度“成冰”公式的适应性研究［J］.低温建筑技术2009，（5）77～80