基于变尺度寻优混合求解算法的航空发动机状态变量模型建立方法

杨征山，仇小杰，王铁，黄金泉

（1.中航工业航空动力控制系统研究所，江苏无锡 214063；2.南京航空航天大学能源与动力学院，南京 210016；3.总参陆航部驻上海地区军事代表室，上海 200233）

0 引言

随着航空发动机技术的发展，对发动机控制技术的研究提出了更高、更复杂的要求。在控制技术领域，包括综合飞行和推进控制、机载自适应模型、降低裕度的逻辑、先进多变量控制技术等方面[1-5]，开展了一系列研究。先进控制算法的研究基础，即如何建立精确的航空发动机状态变量模型成为研究热点[6-9]。

目前求取航空发动机状态变量模型的算法主要包括小扰动法、稳态终值响应法和拟合方法[10-14]。其中，小扰动方法最简单，且易于计算，但结果精度不高；稳态终值响应法在处理线性模型和非线性模型的终值一致问题上效果较好，但不能保证动态过程的一致性；运用拟合法求取的结果精度较高，但需要理想的初猜值，否则会出现拟合过程发散的情况，同时精度随着矩阵维数的增加而降低，耗时也随之增加。

本文将上述3种算法加以综合，最终获得状态变量线性模型。

1 状态变量模型

设航空发动机非线性模型为

式中：x∈Rn、u∈Rr、y∈Rm，分别为发动机状态变量、控制变量、输出量。

当发动机处于某稳态点（x0,u0,y0）工作时，发动机模型为

式（4）即为状态变量线性模型（SVM）。

选取航空发动机风扇转速nF和压气机转速nC为状态变量，发动机供油量Wfm和尾喷管面积A8为控制量，风扇出口总温Tt22、总压Pt22、压气机出口总温Tt3、燃烧室出口总压Pt4、高压涡轮出口总温Tt41、总压Pt41为模型输出量，则式（4）可以表示为

为解决全包线状态下系数矩阵求解繁琐、应用不便和模型中由于物理变量的数量级不同导致系数矩阵畸形的问题，将所有参数进行相似变换并归一化

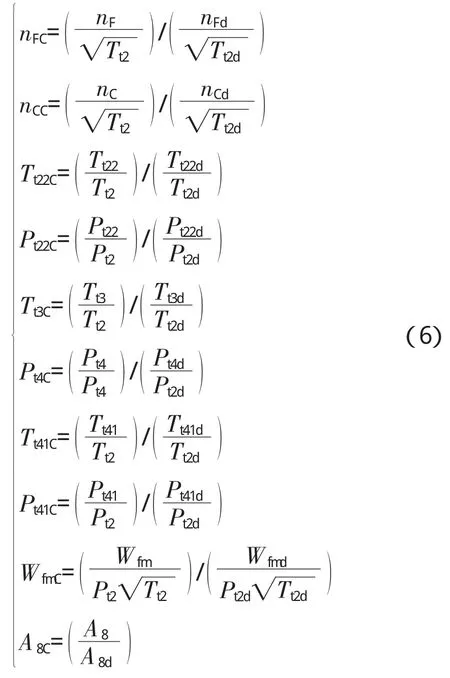
最终经过相似归一化的状态变量线性模型为

2 传统系数矩阵求解方法

2.1 小扰动法

小扰动法的原理是在航空发动机某稳态点处加一扰动，然后用非线性部件级模型进行动态计算，当动态模型的流量达到连续准平衡收敛条件后，求出状态变量的导数和输出变量的增量，计算其与扰动量的比值，求出各系数矩阵。

以求取A、C矩阵为例，分别对状态向量风扇转速nF和压气机转速nC进行扰动，在扰动某一状态向量时，其他状态向量和控制量保持不变，即当扰动风扇转速nF时，令ΔnCC=0、ΔWfmC=0、ΔA8C=0，则

同理扰动压气机转速nC，计算得到a12、a22、c32…、c82的值，最终求得A、C矩阵。采用相同方法求B、D

矩阵，区别是扰动的量由状态量变为控制量。

2.2 稳态终值响应法

系统的特性由状态变量线性模型的系数矩阵决定。其中模型的状态响应特性由A、C矩阵决定，模型的最终稳态响应由B、D矩阵决定。通过设定A、C矩阵值，根据不同输入阶跃情况下模型的稳态输出变化量，应用数学解析方法计算出B、D矩阵值，具体计算公式为

2.3 拟合法

拟合法的求解步骤如下。

（1）状态变量线性模型如式（7）描述，分别求出模型在控制量Wfm和A8作小阶跃时的动态响应解析式；

（2）利用前文建立的非线性部件级模型同样对控制量Wfm和A8作小阶跃，求出部件级模型的动态响应解析式；

（3）利用线性模型动态响应与部件级非线性模型动态响应一致的原则，拟合出状态变量模型。

3 基于变尺度法的混合求解方法

本文将上述3种算法加以综合，利用基于变尺度法的拟合法得到最优的A、C矩阵，使得最终的状态变量线性模型与非线性部件级模型的动态特性相吻合，A、C矩阵的初猜值由小扰动算法求得，而B、D矩阵则通过稳态响应终值法求出并保证状态变量线性模型与非线性部件级模型的稳态稳定输出值完全一致，最终获得状态变量线性模型。

近年来，变尺度优化方法在求解无约束极值问题中取得了良好效果，其主要特点是既避免了计算2阶导数矩阵以及求逆过程，收敛速度又比梯度法的快，对高维问题具有更显著的优越性。

无约束极值问题可以表述为

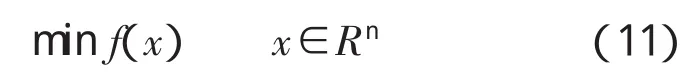
在采用牛顿法求解无约束问题过程中，其优化搜索方向为-[∇2（fxk）]-1∇2（fxk），为了不计算2阶导数∇2（fxk）以及逆矩阵，变尺度方法运用拟牛顿法构造1个H矩阵来逼近2阶导数矩阵的逆阵，变尺度方法的计算步骤如下。

（1）设置初始值x0以及梯度允许误差ε＆gt;0；

（2）若||∇（fx0）||≤ε，则x0为近似极小值，停止迭代，若否，继续下1步；

λ得到λ0，从而得到下个近似点

（4）迭代到第k步，得到近似点xk，计算出∇（fxk），若||∇（fxk）||≤ε，则xk即为最优值，停止迭代，若否，计算

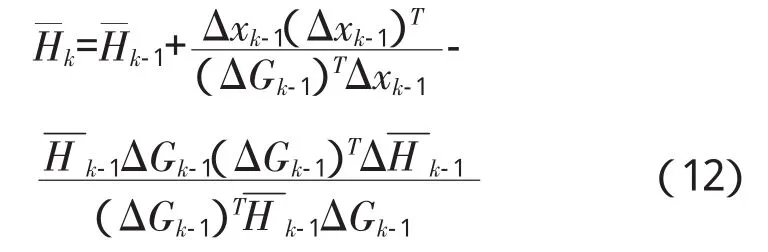
式中：ΔGk-1=∇f（xk）-∇f（xk-1），得到和λk，计算出 xk+1=xk+λkPk；

（5）若xk+1满足精度要求，则xk+1为最优解，若否，转到第（4）步。

基于变尺度法的发动机线性模型混合求解方法计算步骤如下。

（1）对发动机非线性部件级模型的控制量Wfm和A8分别作小阶跃[Δu1（t），Δu2（t）]

计算部件级模型的动态响应偏差向量为Δy(t)=[ΔnFC（t），ΔnCC（t），ΔTt22C（t），ΔPt22C（t），ΔTt3C（t），ΔPt4C（t），ΔTt41C（t），ΔPt41C（t），ΔFnC（t），ΔSmC（t）]。

式中：t=0，T，…，nT，T为采样时间；

（2）利用小扰动法求取A、C矩阵的初猜值A0、C0；

（3）利用稳态终值响应法中的式（9）、（10）求出B0、D0，得到线性模型；

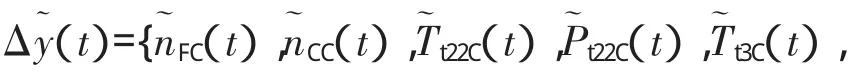
（5）将（1）和（3）中的动态响应数据Δy（t）和Δy˜（t）作为样本，采用变尺度法，优化如式（14）所示的目标函数

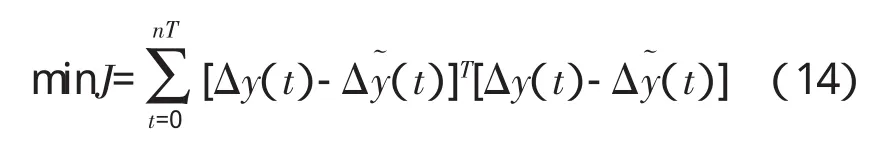
即计算与部件级非线性模型响应偏差平方和最小的线性模型系数矩阵值。通过优化，若满足精度要求，得到线性模型系数矩阵（A，B，C，D）；若不满足精度要求，重复第（4）、（5）步。

限于篇幅，这里仅给出地面标准大气条件下，Wfm=1.8kg/s和A8=0.25m2工作点处的线性模型系数矩阵求解过程。

（1）对发动机非线性部件级模型的控制量Wfm和A8分别作小阶跃[Δu1（t），Δu2（t）]

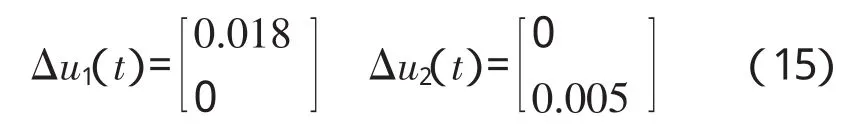
计算部件级模型的动态响应偏差向量为Δy（t）；

（2）利用小扰动法求取A、C矩阵的初猜值A0、C0

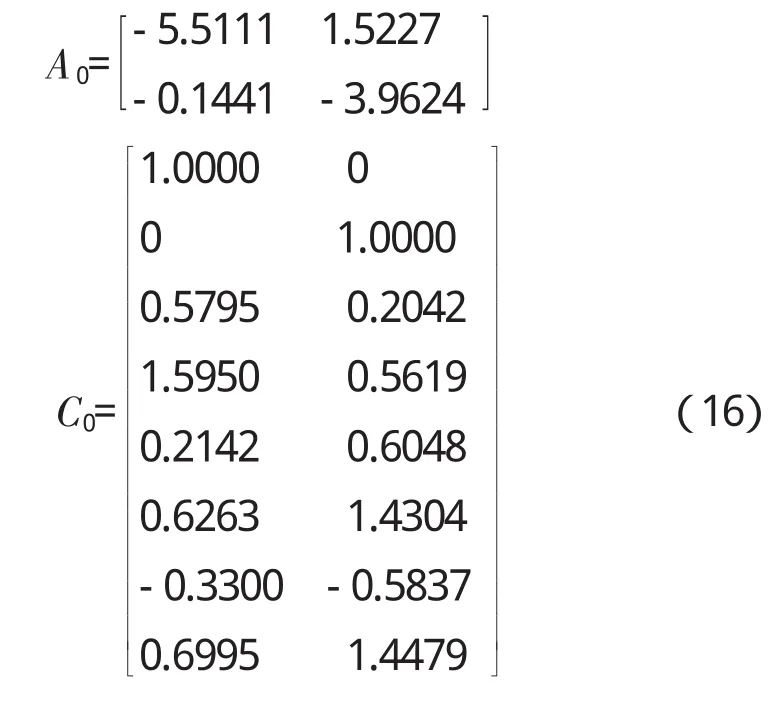
（3）由式（9）、（10）求出B0、D0

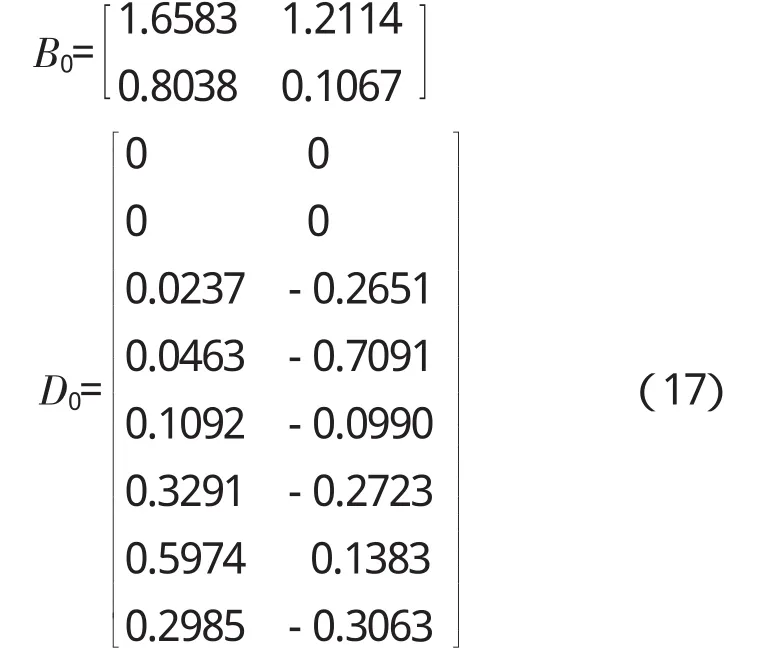
得到线性模型系数矩阵初猜值A0，B0，C0，D0；

（4）对此线性模型的控制量Wfm和A8分别作小阶跃[Δu1（t），Δu2（t）]

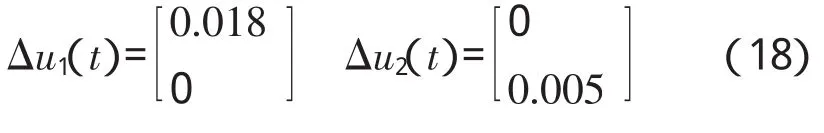
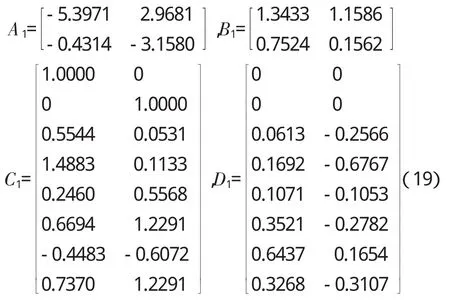
（5）利用变尺度算法优化如式（14）的目标函数，得到第（1）步优化所得线性模型系数矩阵（A1，B1，C1，D1）

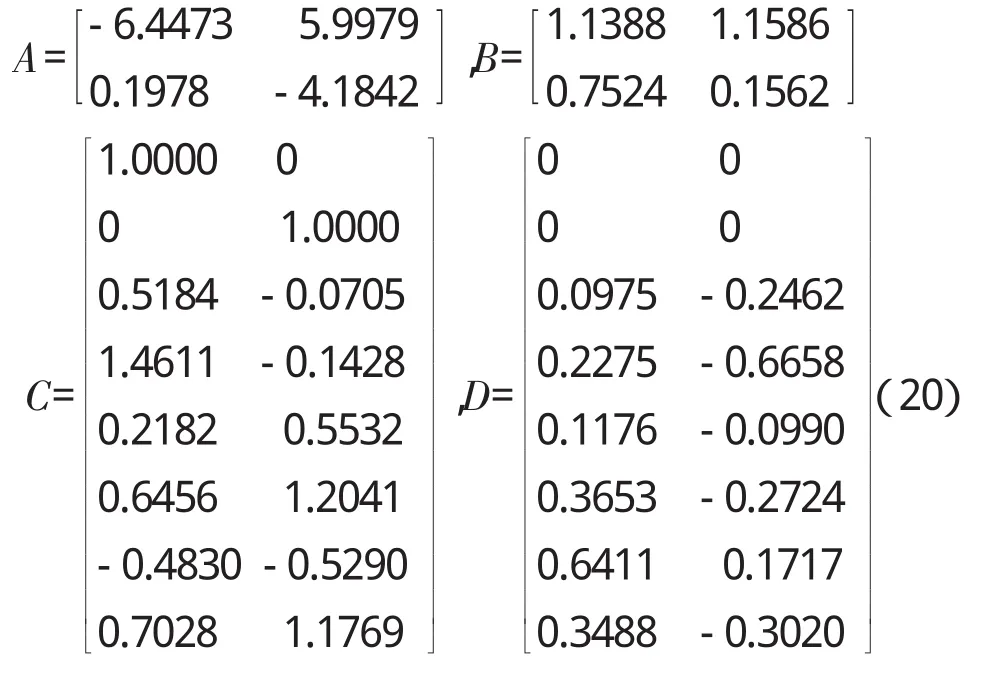
不满足精度要求，重复第（4）、（5）步操作，直至满足精度要求，得到线性模型的系数矩阵（A1，B1，C1，D1）

4 状态变量模型仿真

模拟发动机非线性部件级模型[15]和状态变量线性模型在H=0、Ma=0、Wfm=1.8kg/s和A8=0.25m2工作点上，分别作2个控制量的小阶跃仿真（其中供油量Wfm阶跃0.5%，尾喷管面积A8正阶跃1.5%），比较2个模型的输出响应吻合程度，检验基于变尺度法的混合求解方法计算出的状态变量线性模型的精确度，仿真结果如图1、2所示。

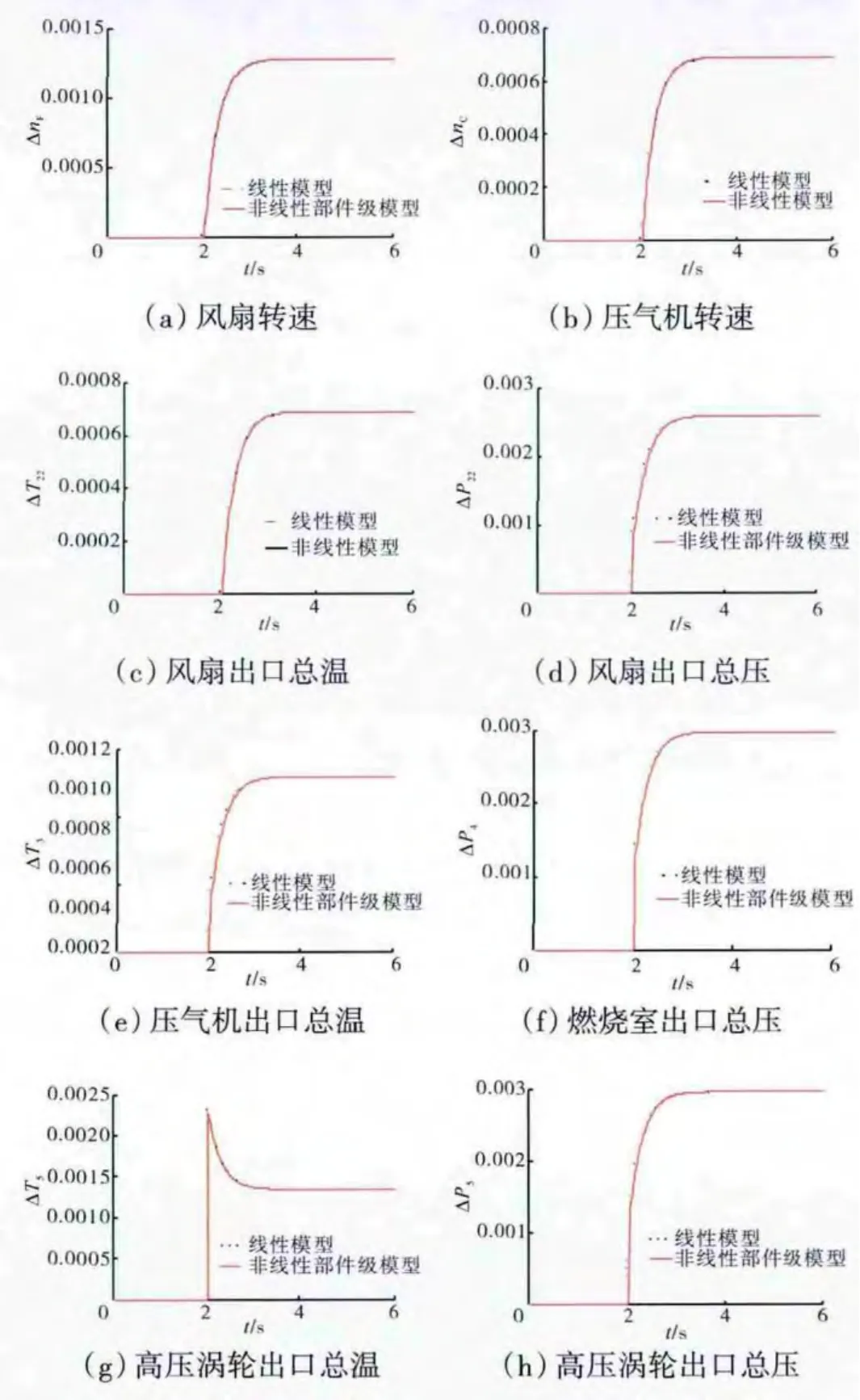
图1 燃油小阶跃线性模型响应与非线性模型响应

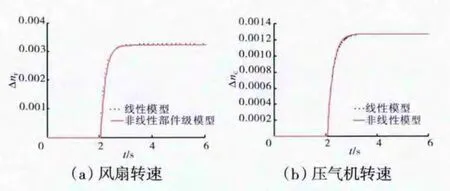
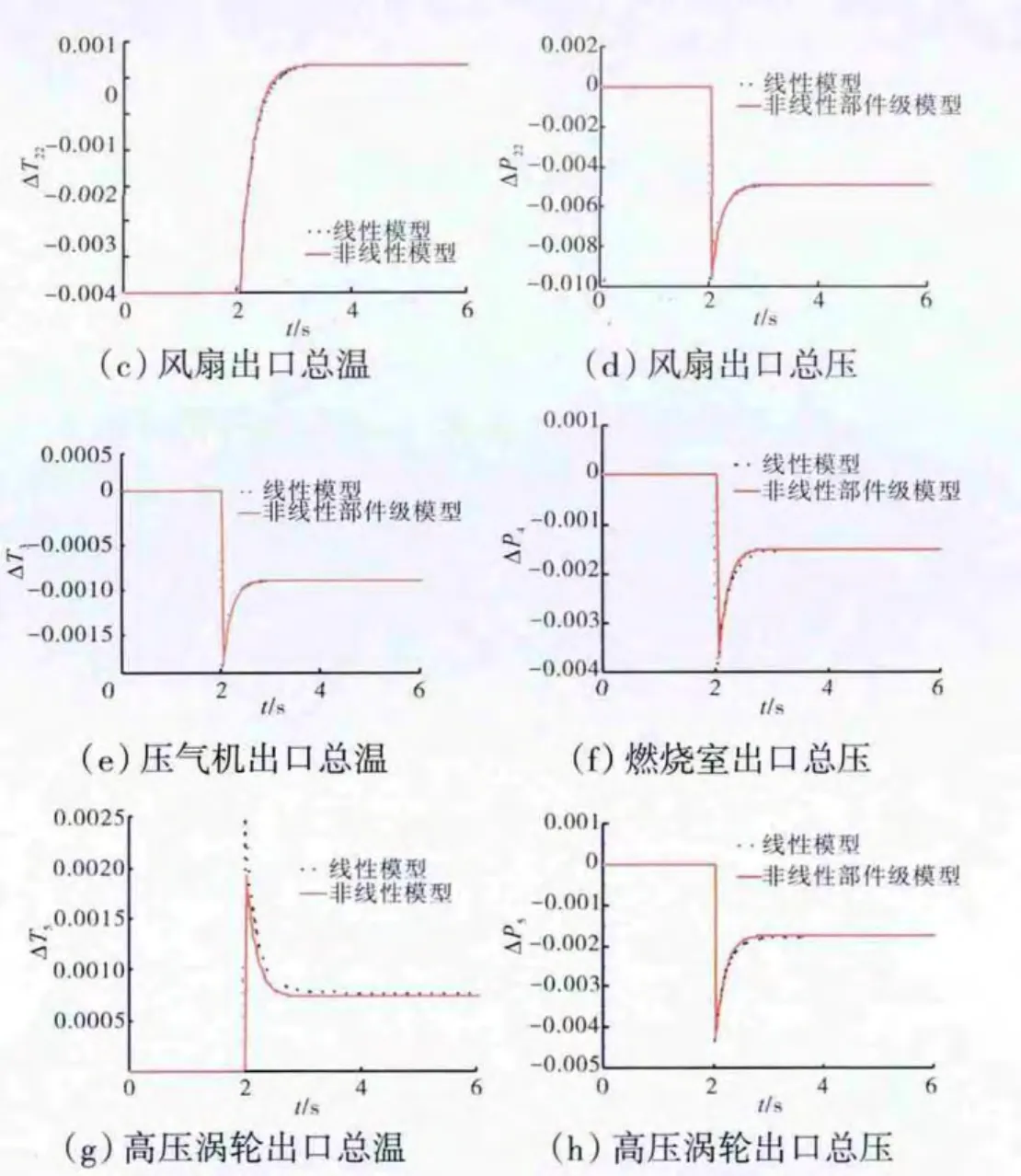
图2 尾喷管面积小阶跃线性模型响应与非线性模型响应

从仿真结果中可见，本文提出的基于变尺度法的混合求解方法计算的线性模型与非线性部件级模型不仅在动态过程响应中吻合良好，而且能够保证发动机最终稳定值的一致性，具有较高的精度。

5 结束语

本文研究了发动机状态变量线性模型的求解方法，分析了传统小扰动法、稳态终值响应法和拟合法的优缺点，提出了基于变尺度法的混合求解方法。该方法能避免小扰动方法精度不高、稳态终值响应法动态过程不一致以及传统拟合法随着需要拟合的矩阵维数增加而精度下降、拟合时间增加的缺点。仿真结果表明，本文方法不仅在动态过程响应中吻合良好，具有较高的稳态精度，而且能够保证发动机最终稳定值的一致性，具有良好的应用前景。

[1] Skira C A, Agnello M. Control system for the next century’s fighter engines [J]. Transactions of the ASME Journal of Engineering for Gas Turbines and Power, 1992，114（4）：749-754.

[2] Paseal G. A linear matrix inequality approach to H ∞control[J].International Journal of Robust and Nonlinear Colltrol，1994，4（4）：421-448.

[3] Turner M C, Walker D J, Alford G. Design and ground-base simulation of an H ∞ limited authority flight control system for the Westland Lynx helicopter [J]. Aerospace science and Tech nology，2001，5（3）：221-234.

[4] Conners T R. Thrust stands evaluation of engine performance improvement algorithms in an F-15 airplane[R]. AIAA-92-3747.

[5] Orme J, Schkolnik G. Flight assessment of the onboard propulsion system model for the performance seeking control algorithm on an F-15 aircraft [R]. AIAA-95-2361.

[6] Leibov R. Aircraft turbine engine linear with uncertain engine values [J]. IEEE Transaction on Automatic Control，2002，47（8）：1367-1369.

[7]王磊，郭迎清，陆军，等.用改进子空间辨识法建立航空发动机模型[J].计算机仿真，2012，29（12）：75-79.

WANG Lei, GUO Yingqing, LU Jun, et al. Establishment of aeroengine model with improved subspace model identification method [J]. Computer Simulation，2012，29 （12）：75-79. (in Chinese)

[8]李秋红，孙健国.基于遗传算法的航空发动机状态变量模型建立方法[J].航空动力学报，2006，21（2）：427-431.

LI Qiuhong，SUN Jianguo. Aeroengine state variable modeling based on the genetic algorithm[J]. Journal of Aerospace Power，2006，21（2）：427-431. (in Chinese)

[9] Sugiyama N. Derivation of ABCD system matrices from nonlinear dynamic simulation of jet engine[R]. AIAA-92-3391.

[10]郑铁军，王曦，李秀芹，等.建立航空发动机状态空间模型的修正方法[J].推进技术，2005，26（1）：46-49.

ZHENG Tiejun, WANG Xi, LI Xiuqin, et al. Modified method of establishing the state space model of aeroengine[J]. Journal of Propulsion Technology，2005，26（1）：46-49. (in Chinese)

[11]苗卓广，谢寿生，吴勇，等.基于改进粒子群算法的航空发动机状态变量建模[J].推进技术，2012，33（1）：73-77.

MIAO Zhuoguang, XIE Shousheng, WU Yong, et al. Aeroengine state variable modeling based on the improved particle swarm optimization [J]. Journal of Propulsion Technology，2012，33（1）：73-77. (in Chinese)

[12]陆军，郭迎清，陈小磊.线性拟合法建立航空发动机状态变量模型[J].航空动力学报，2011，26（5）：1172-1177.

LU Jun，GUO Yingqing，CHEN Xiaolei. Establishment of aeroengine state variable model based on linear fitting method [J]. Journal of Aerospace Power，2011，26（5）：1172-1177. (in Chinese)

[13]鲁峰，黄金泉，佘云峰.航空发动机状态变量模型的QPSO寻优混合求解法[J].推进技术，2011，32（5）：722-727.

LU Feng, HUANG Jinquan, SHE Yunfeng. State space modeling based on QPSO hybrid method for aeroengines[J]. Journal of Propulsion Technology，2011，32 （5）：722-727. (in Chinese)

[14]张海波，杨小龙，林一晖.一种求取发动机状态变量模型的改进拟合法[J].航空动力学报，2011，26（8）：1907-1913.

ZHANG Haibo，YANG Xiaolong，LIN Yihui. An improved method of identification for aeroengine’s state variable model [J]. Journal of Aerospace Power，2011，26（8）：1907-1913. (in Chinese)

[15]周文祥，黄金泉，窦建平，等.面向对象的涡扇发动机及控制系统仿真平台[J].航空动力学报，2007，22（1）：119-125.

ZHOU Wenxiang，HUANG Jinquan，DOU Jianping，et al.Object-oriented simulation platform for turbofan engine and its control system [J]. Journal of Aerospace Power,2007,22（1）：119-125. (in Chinese)