一道例题的教育价值

赵冬歌 沈福刚

（1.河北大学 质量技术监督学院，河北 保定 071002；2.河北大学 化学与环境科学学院，河北 保定 071002）

同济大学数学系编写的 《高等数学》（本科少学时类型）（第三版）（下册）教材第158页的例1是这样的［1］：计算，其中L 为上半圆弧 x2+y2=ax，y≥0（图 1）

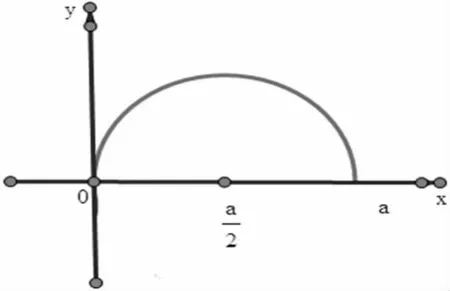
图1

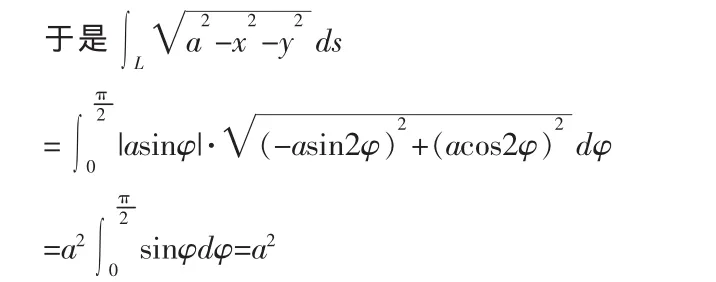
如果不认真思考，就会此题解得很有条理，但是通过仔细思考，就会发现本题在求解过程中存在着矛盾。那是什么矛盾呢？本题里所给出圆的方程：x2+y2=ax，化为它的一般方程（，于是想当然地画出了上半圆弧，位于第一象限，但是仔细思考一下，这是在假定a＞0的前提下（可是题目却没有给出a＞0），然后写出上半圆弧的极坐标方程 ρ＝acosφ （0≤φ≤）。 然而在接下来计算的过程中，遇到a2的开方时，计算时却没有将a开出来，而是写成|asinφ|，说明这时又考虑到a可能为正也可能为负。同时，又巧妙地躲过了关于a是正是负的讨论。整个解题过程中，关于a的正负问题立场不坚定，模模糊糊。也许关于a的正负不是本次课的重点，本次课的重点是关于对弧长的曲线积分如何计算。但是这样解题是不严谨、不合理的，考试时这样解题是不全面，不正确的。

严格来说，对于这道题应该考虑a的正负，合理的解答应该是这样的：

实际上，编者的意图是要在a＞0的条件下求解的，可能是因为一时的疏忽忘了加a＞0这个限定条件。但是没有这个条件就该分两种情况解答。

对于这道例题，老师可以首先引导学生来检查这道例题的解题过程是否严谨，是否正确，如果不正确那么问题在哪里。通过老师的启发，学生也能发现这道例题上不严谨的地方，这样把他们的积极性调动起来了，能把课本上的错误找出来使学生体会到成就感［2］。这时候就调动起学生的主动性，老师这时要教导学生：“尽信书则不如无书”，学好任何课程任何知识不能只靠看课本和听老师讲课，不能仅仅被动地去接受，而应该自己认真地阅读，用心思考，任何书都可能存在错误，我们要自己根据所学知识发现书中错误的地方。老师借此机会向学生强调数学学科的严谨性，数学学科相对其它学科最大的特点就是数学学科的严谨性［3］，是就是，不是就不是，没有中间地带。老师还可以进一步地要求学生写出完整的求解过程。这个时候学生的积极性和主动性被调动起来［4］，大脑活跃起来，他们很愿意把这个正确的答案完完整整地写下来，这个过程培养了他们的严谨性。当然在求解过程中，他们也会遇到困难，比如a＜0，圆的极坐标方程中极角的范围，这是他们通过努力可以解决的。同时，他们又重温了一下对弧长的曲线积分的计算，这个过程是积极主动的，学生不仅学到了知识，也在思想上得到教育。

由此可见，通过这道教材上的错误例题，老师经过精心引导和设计［5］，不仅调动了学生学习的积极性，而且也教育学生不能盲目地相信教材，教材本身也有不完善的地方。学生经过努力推导出了完整的答案，不仅数学知识得到了巩固和提高，而且在这个过程中体会到成就感，为数学学科以及其它学科的学习提高了兴趣和信心！也培养了学生严谨的逻辑思维能力！在老师的引导下，学生从这道例题中受益匪浅！

［1］同济大学数学系.高等数学[M].3版.北京：高等教育出版社.

［2］霍春光.如何提高学生对高等数学的兴趣[J].辽宁教育行政学院学报,2009，26（6）：100-101.

［3］李国成,关于高等数学课程教学的问题与思考[J].河北大学成人教育学院学报，2007,9：72-74.

［4］胡嘉卉，孙彩贤.高等数学教学改革研究与探索[J].太远城市职业技术学院学报，2012,9：144.

［5］陈之兵.一道例题的引申和启发[J].高等数学研究，2011，14（5）：41-42.