回归分析模型及聚类分析法

韩宝燕

(山东工艺美术学院 公共课教学部，山东 济南250000)

1 非商品支出的含义

居民消费支出是指城乡居民个人和家庭用于生活消费以及集体用于个人消费的全部支出。商品性支出主要是居民用于购买商品的支出，非商品性支出主要就是指居民享受文化服务和生活服务的支出。非商品支出能从一个侧面反映居民消费结构的变化和经济水平的发展。

2 多元回归分析方法

2.1 多元回归分析的概述

回归这个词最早是由英国著名统计学家Francis Galton在19世纪末期研究孩子及他们的父母的身高时提出来的。在研究时，Galton发现父母的身材高，他们的孩子身材也高，身材矮的父母孩子身材也矮。但是，他发现，该身材父母的孩子的身高并不像他们父母那般高，而身材矮的父母的孩子的身高并不像他们父母那样矮，而是集中的趋向于某一值，Galton把这种趋势称为回归效应，至此回归一词产生。后来，他发展研究两个数值变量，这种方法也就是后来的回归分析。

回归分析是以概率论与数理统计为基础迅速发展起来的一种应用型较强的学科。现在，回归分析被广泛的应用于经济方面的研究。在现在的经济研究中，回归分析通常可以与聚类分析一起使用，在原始的分类学中，人们是根据经验和专业知识来进行定性分析，很少使用数学工具，但是随着人们不断深入的去了解自然和社会，要处理的数据原来越复杂，相互关系越来越复杂，分类也越来越细，对数据分类的要求也变得越来越高，这时仅仅依靠经验和专业知识进行分类是不够的，这时数学便引入到数据分析中，便形成了数据分类学。这种方法是对分析对象进行定量的研究，由于这种方法不仅能够用于分类，还能应用于其他领域，于是人们认为用“聚类分析”这个词更为合适。

2.2 多元回归分析模型的一般形式

回归分析方法是在众多相关变量中，根据实际问题的要求，考察其中一个或几个变量与其余变量的依赖关系。如果只要考察某一个变量与其余多个变量的相互依赖关系。我们称为多元回归问题。

多元回归分析是研究因变量Y与k个自变量x1，x2，…，xk的相关关系，而且总是假设因变量y为随机变量，而x1，x2，…，xk为一般变量。

如果被解释变量（因变量）y 与 k 个解释变量（自变量）x1，x2，…，xk之间有线性相关关系，那么他们之间的多元线性总体回归模型可以表示为：

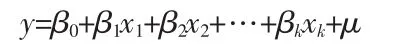
式中，β0，β1，β2，…，βk是 k+1 个未知参数，又称为回归系数；μ 是随机误差项。 如果我们将 n 组实际观测数据（yi，x1i，x2i，…，xki)i=1，2，…，n代入式中可得到下列形式：

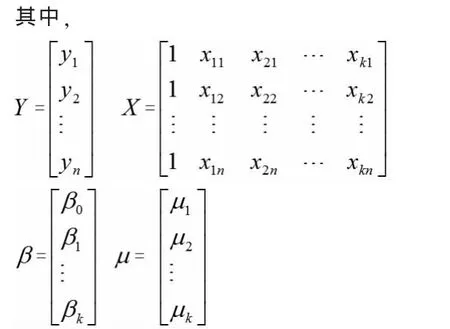
2.3 逐步回归分析

在多元线性回归分析中，并不是所有的自变量都对因变量都有显著地影响，这就存在着如何挑选出对因变量有显著影响的自变量问题。从20世纪60年代开始，关于回归自变量的选择成为数理统计中研究的热点问题，人们提出了一些较为简便、实用、快速的选择“最优”方程的方法。人们所给出的方法各有优缺点，至今还没有绝对最优的方法，目前常用的方法有“前进法”、“后退法”、“逐步回归法”，而逐步回归法最受推崇。

逐步回归的基本思想是“有进有出”。具体做法是将变量一个一个引入，引入变量的条件是其偏F统计量或t统计量经检验是显著的。即每引入一个自变量后，对已经被选入的变量要进行逐个检验，当原引入的变量由于后面变量的引入而变得不在显著时，要将其剔除。引入一个变量或从回归方程中剔除一个变量，为逐步回归的一步，每一步都要进行偏F检验或t检验（二者等价），以确保每次引入新的变量之前回归方程中只包含显著的变量。这个过程反复进行，直到既无显著的自变量选入回归方程，也无不显著自变量从回归方程中剔除为止。这样就保证了最后所得的回归子集是“最优”回归子集。

在逐步回归法中需要注意的是引入和剔除自变量的显著性水平应该有所不同，一般要求引入自变量的显著性水平α1小于剔除自变量的显著性水平α2，否则可能产生“死循环”的现象。

3 聚类分析方法

3.1 聚类分析的概述

聚类分析是统计学中研究的“物以类聚”问题的多元统计分析方法。聚类分析在统计分析的应用领域中已经得到了广泛的应用。

聚类分析指将物理或抽象对象的集合分组成为由类似的对象组成的多个类的分析过程。它是一种重要的人类行为。聚类分析的目标就是在相似的基础上收集数据来分类。聚类源于很多领域，包括数学，计算机科学，统计学，生物学和经济学。在不同的应用领域，很多聚类技术都得到了发展，这些技术方法被用作描述数据，衡量不同数据源间的相似性，以及把数据源分类到不同的簇中。

3.2 Q型聚类分析

Q型聚类是对样本进行聚类，它使具有相似特征的样本聚集在一起，使差异性大的样本分离开来。分类的结果是直观的，且比传统分类方法更细致、全面、合理。

3.3 系统聚类法的基本思想和基本步骤

设有n个样品，每个样品测得m项指标。系统聚类方法的基本思想是：首先定义样品间的距离（或相似系数）和类与类之间的距离。初始将n个样本看成n类（每一类包含一个样品），这时类间的距离与样品间的距离是等价的；然后将距离最近的两类合并成为新类，并计算新类与其他类的类间距离，再按最小距离准则并类。这样每次缩小一类，知道所有的样品都聚成一类为止。

由以上系统聚类法的基本思想，即可得出它的基本步骤如下：

（0）数据变换：数据变换的目的是为了便于比较和计算，或改变数据的结构。定义样品间的距离和类与类之间的距离。（1）计算n个样品两两间的距离，得样品间的距离矩阵D(0),初始的n个样品各自构成一类。 （2）找出距离最小元素，设为 Dpq，即将 Gp、Gq合并为一新类，记为Gr。（3）按类与类之间的距离计算新类与其他类的距离，重复步骤（2）和（3），知道类的总个数为 1 时转到步骤（4）。（4）画谱系聚类图。（5）决定分类的个数及各类的成员。

［1］高惠璇.应用多元统计分析[M].北京：北京大学出版社，2005.

［2］薛薇.统计分析与SPSS的应用[M].2版.北京：中国人民大学出版社，2008.

［3］金玉国.计量经济学[M].北京：经济科学出版社，2006.

［4］何晓群.多元统计分析[M]北京：中国人民大学出版社，2008.

［5］国家统计局.中国统计年鉴[M].北京：中国统计出版社.

［6］朱建平.应用多元统计分析[M].北京：科学出版社，2006.

［7］陈捷.中国城镇居民消费结构变化的定量分析[J].统计与决策，2003.