基于联合聚类和矩阵分解的协同过滤算法研究

赵广艳，李禹生，韩 昊

(武汉轻工大学数学与计算机学院，湖北武汉430023)

协同过滤个性化推荐是电子商务个性化推荐中应用最多的技术之一。近年来，国内外学者对协同过滤算法做了大量研究工作，并取得了丰硕成果，许多大型电子商务网站，如 Amazon，Ebay，Levis，阿里巴巴，当当网上书店等都采用了各种形式的推荐系统功能。伴随着电子商务规模的增大，用户与项目的数量急剧上升，协同过滤算法面临的关键挑战是数据稀疏性，算法的可扩展性。由于算法的计算量大，导致算法的性能急剧下降。基于用户聚类的协同过滤推荐算法［1］，与传统的协同过滤算法相比，提高了推荐速度和质量，但是只考虑了用户相似性。王辉等提出了个性化服务中基于用户聚类的协同过滤推荐［2］，该算法对可扩展性和数据型稀疏性方面进行了一定改进，但是效率和准确度还有待提高。

在协同过滤推荐算法中，需要处理的数据都是根据用户-项目评分矩阵来进行的。针对协同过滤算法存在的可扩展性和数据稀疏性，笔者引入联合聚类(BlockClust，简称BC)和带正则化的迭代最小二乘法(alternating-least-squares with weighted-regularization，简称AW)，提出了一种基于BC-AW的协同过滤推荐算法，有效缓解了传统算法难以并行化、可扩展性差的问题，整个算法主要分为两步:①在原始评分矩阵中进行用户—项目两个维度的联合聚类，聚类后生成具有相同模式评分块的若干子矩阵，联合聚类后的子矩阵规模远小于原始评分矩阵，大幅度降低预测阶段计算量。②在联合聚类后生成的每个子矩阵上分别利用带正则化的迭代最小二乘法的协同过滤算法来预测子矩阵中的未知评分，进而进行推荐。

1 联合聚类

怎样处理大量并且很稀疏的训练数据是协同过滤算法面临的关键问题，因此通过联合聚类的方法将原始训练数据划分成数据规模较小、相似度较高的子矩阵是一种有效的方法。对于协同过滤算法问题，联合聚类算法应用到协同过滤算法有两大优势:①需要处理的数据规模大量减少，算法的复杂操作会变得相对容易;②有效缓解评分稀疏性。

协同过滤算法，就是处理用户—项目评分矩阵，联合聚类的目的就是缩小子矩阵内部评分数据间的差异。以评分模式为标准的联合聚类［3］采用的思路是扫描用户—项目评分矩阵中已经有的评分，进行行聚类与列聚类两个步骤进行概率计算，每次迭代都需要重新评估计算用户、项目、评分这三者属于每个子矩阵的概率直至收敛。将每个评分分配到所求概率最大的那个子矩阵，不同的子矩阵可能包含同一个用户—项目。每个子矩阵的用户、项目、评分会组成新矩阵，此时的新矩阵已经是高相似性评分的子矩阵，可以快速有效应用计算。

联合聚类后原来非常稀疏的用户—项目评分矩阵转变成为K个规模较小的子矩阵，每个子矩阵的内部评分相似度较高并且相对稠密，从而可以进行有效的降维。在下一阶段的评分预测也会变更容易、更准确。

对评分模式为标准的联合聚类，扫描评分矩阵，计算每个评分属于某子矩阵的概率p(k|u，v，r)，要判定一个评分属于某子矩阵，需要考虑与评分所关联的用户—项目属于该子矩阵的概率分别为p(k|u)与p(k|v)，以及该评分值出现在这个子矩阵中的概率p(r|k)。计算公式如下:

其中，u为当前用户，v为当前项目，r为评分值，r'为1到5的整数，k为当前聚类，k'为累加时的当前聚类，U(v)为给项目v评过分的所有用户集合，V(u)为用户u已评过分的所有项目集合，为了防止分母为0需要设置超参数α，β，θ，可根据具体情况设定，在下面的实验中统一设为0.000 000 1。

2 带正则化的迭代最小二乘法的矩阵分解

在预测阶段，评分预测可以选用很多种矩阵填充方法，例如简单的k-最近邻模型预测方法，基于传统的矩阵分解模型的方法。通过考虑，这里采用改进的矩阵分解算法(alternating-least-squares with weighted-regularization，简称 AW)［4］来进行评分预测。对于联合聚类后的子矩阵，AW方法可以在极短的时间内收敛到局部最小。

给定一个矩阵R，Rij为矩阵的元素，Ri·为矩阵R的第i行，R·j为矩阵的第j列，RT为矩阵R的转置。R－1为矩阵的逆。矩阵 A∈Cm×d、B∈Cn×d分别为用户和项目矩阵的特征矩阵，I为一个d×d的单位矩阵。

为了能够找到低秩矩阵X来最大程度的接近矩阵R，最小化下面损失函数

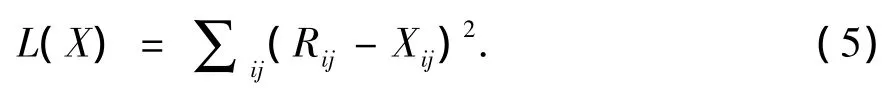
其中，X=ABT，d为特征数目，一般情况下d＜＜r，r为矩阵R 的秩，r≤min(m，n)，Xij为X 矩阵的元素。

式(5)中(Rij－Xij)2是低秩逼近中常见平方误差项，由X=ABT把式(5)改成有效并且快速的求解最优化问题。

给式(6)加上正则化项来预防过拟合现象，则式(6)可以改写成:

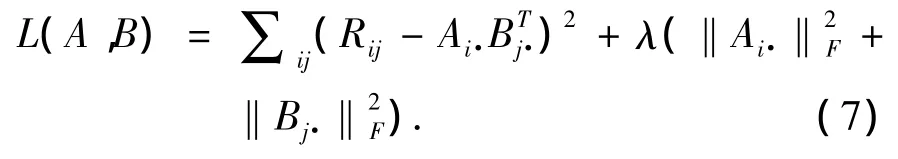
固定 B，对 Ai·求导，得到求解 Ai·的公式如式(8)所示。

同理，根据式(8)固定A，可以得到Bj.的公式为:

3 基于BC-AW的协同过滤推荐算法

为了预测评分矩阵中的未知项，采用两阶段算法。具体算法如下:

第1阶段联合聚类

输入:用户—项目评分矩阵R，子矩阵个数K。

输出:K个子矩阵

Step1:随机初始化用户u，项目v，评分r共同属于聚类k的概率p(k|u，v，r)，使得

Step2:根据式(2)计算用户u属于聚类k的概率p(k|u);

Step3:根据式(3)计算用户v属于聚类k的概率p(k|v);

Step4:根据式(4)计算分值概率p(r|k);

Step5:根据式(1)计算 p(k|u，v，r)，并选取概率最大的k作为该评分的子矩阵;

Step6:跳转到Step2，直至收敛，否则结束程序。

第2阶段:基于AW的协同过滤评分预测

输入:子矩阵所对应的用户-项目评分矩阵;

输出:预测评分矩阵X;

Step1:随机初始化A、B;

Step2:用式(8)、式(9)反复迭代更新A、B，直到收敛或迭代次数足够多而结束迭代;

分析基于BC-AW的协同过滤推荐算法，可以看出该算法的第2阶段的关键步骤是Step2，运用公式反复迭代更新A和B直到收敛或迭代次数足够多而结束迭代。通过式(8)、式(9)可分析出，可以对矩阵A、B进行分割，因为每次调用公式只是计算更新矩阵A、B的一行值。把矩阵A、B分成多个具有相同列长的矩阵来进行并行运算，从而缓解了传统的基于矩阵分解的协同过滤算法难以并行化、可扩展性差的问题。

4 实验结果分析

4.1 实验数据集和度量标准

该文选取MovieLens数据集评估改进算法的性能，MovieLens是美国的明尼苏达州立大学(University of Minnesota)的GroupLens研究小组搜集的电影评价数据集。该数据集中包括943位用户对1682部电影的十万条评分数据(评分值为1到5的整数)，5表示评分最好，1表示评分最差，每个用户至少给出20个评分。

将原数据集分为训练集与测试集，从原数据集中随机抽取80%的评分数据作为一个训练集，记为Train80;原评分数据中除Train80以外的数据集构成测试集，记为Test20;把Train80中的评分数据集中的1/2抽取出来作为另一个训练集，记为Train40。通过训练集生成模型，对测试集进行评分预测，根据预测评分的结果与原实际评分之间的偏差来度量预测的准确性。本文采用的评估方法为均方根误差 RMSE［5］(Root Mean Square Error)的方法，RMSE值越小，代表准确度越高。假设n表示将要评估预测评分的项目数量，用户对n个项目的预测评分值集合为 {p1，p2，...，pn}，实际评分值集合为 {q1，q2，...qn}，RMSE 的计算公式如下:

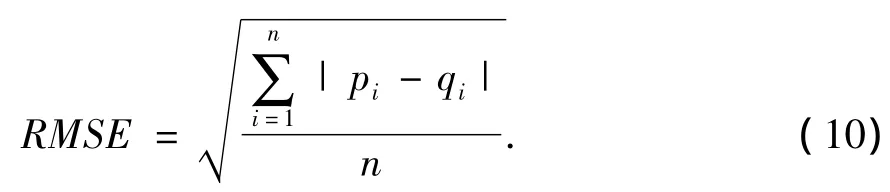
4.2 结果分析

评价推荐系统推荐质量的度量标准采用式(10)统计度量方法中的均方根误差 RMSE。对MovieLens进行评分预测，算法的超参数设置如下:α=β=θ=0.000 000 1。对于子矩阵个数K的设置做了一组实验，实验结果如图1所示。

图1 子矩阵个数K与RMSE的关系

由图1可知，在各种实验条件下，在训练集为Train80类别数为50的情况下RMSE最小，系统推荐质量最好。在以下的实验中，采用类别数K为50。

将基于BC-AW的协同过滤算法的有效性进行对比实验，参与对比实验的算法包含Hofmann提出的潜在语义模型协同过滤算法(LSM)［6］和基于矩阵分解的协同过滤算法(ALS-WR)。各个算法均分别在Train80，Train40训练集上训练，在Test20上测试得到RMSE值，实验数据如图2所示。

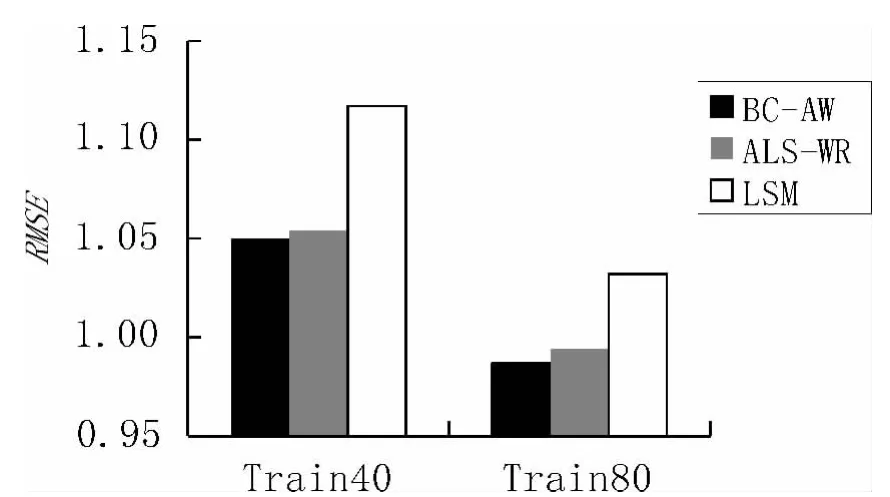
图2 不同算法性能比较结果

从图2可以看出，本算法的均方根误差较小，说明推荐准确度得到了一定的提升。

5 结束语

该文提出了基于联合聚类和迭代最小二乘法的两阶段协同过滤算法。首先对原始评分数据进行基于用户—项目的联合聚类，即以评分值为标准，寻找具有相同模式的评分块，从而把原始评分矩阵划分成为相互可能有交叉的评分子块，聚类后的矩阵规模远小于原始评分矩阵，可快速灵活的进行评分预测。在评分预测阶段，采用基于AW的协同过滤算法的评分预测，并分析了其可扩展性及抗稀疏性问题。分别在Train80，Train40的训练集下采用不同类别数K下，比较了均方根误差，找出了效果最好的条件。在效果最好的条件下，和几个经典协同过滤算法进行比较。实验结果表明，BC-AW算法优于几个经典的协同过滤算法。

［1］李涛，王建东，叶飞跃，等.一种基于用户聚类的协同过滤推荐算法［J］.系统工程与电子技术，2007，29(7):1178-1182.

［2］王辉，高利军，王听忠.个性化服务中基于用户聚类的协同过滤推荐［J］.计算机应用，2007，27(5):1225-1227.

［3］吴湖，王永吉，王哲，等.两阶段联合聚类协同过滤算法［J］.软件学报，2010，21(5):1042-1054.

［4］李改，李磊.基于矩阵分解的协同过滤算法［J］.计算机工程与应用，2011，47(30):4-7.

［5］Koren Y.Factorization meets the neighborhood:A multifaceted collaborative filtering model［C］//Proc of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，2008:426-434.

［6］Hofmann T.Latent semantic models for collaborative filtering［J］.ACM Trans actions on Information Systems，2004，22:89-115.