增强型轻量级防窃听安全网络编码算法

王 骁

（中国电子科技集团公司第20研究所，西安 710068）

0 引 言

网络编码［1］允许中间节点将各个入边上的数据包进行混合后再发送到其出边上，这与传统的路由转发模式不一样。Li，Yeung和Cai表明，一个足够大的有限域上的线性网络编码足以达到多播容量［2］。为了运算的方便和代数结构的简明性，绝大多数研究都集中于线性网络编码。Ho等人提出一种在实际应用中容易实现的分布式网络编码方法［3］，即随机网络编码（RLNC）。在RLNC中，中间节点在编码域上独立随机选取编码系数，对收到的数据包进行线性编码，当编码域的大小达到28或者216时，RLNC可以以接近于1的概率达到多播容量。网络编码在提高了吞吐量和可靠性的同时，也有着相应的安全问题，比如防窃听安全问题。

针对防窃听安全问题，文献［4］首次研究了达到信息论意义安全的安全网络编码，假定窃听者的窃听能力受限，并给出安全网络码的构造方法。Feldman等人表明构造一个安全网络码等价于寻找一个有着广义距离性质的线性码，并指出通过牺牲少量的带宽就能在相对小得多的有限域上构造安全网络码［5］。Ngai等人将广义汉明重量扩展到线性网络码上［6-7］。Bhattad和 Narayanan则考虑了在实际应用中更一般的弱安全网络编码［8］，即窃听者得不到源消息的任何有意义的信息。Harada和Yamamoto基于强安全斜坡秘密共享方法提出了强安全网络编码的概念，并表明弱安全事实上是强安全的一种特殊情况［9］。Silva和Kschischang基于秩测度码提出一般化的安全网络编码［10］，可以用于任意网络的源节点预编码且不需要对网络码做任何改变。

在实际情况中，窃听能力往往不受限制，而计算能力却受到限制。此外，网络容量和计算资源都是宝贵的资源。为解决这个问题，文献［11］～［13］将密码学方法和网络编码结合起来，提出了能够防全局窃听者的更为实用的方法，并且不用更改中间节点的随机编码方式。文献［11］提出的最小开销方法（MOS）安全性极佳，但是由于要加密整个消息，从而导致加密容量很高。文献［12］提出的方法（P-coding）则利用置换函数来抵抗窃听攻击，且没有空间开销，但其加密容量同样很高。文献［13］提出了轻量级安全方法（SPOC），只需加密一个短小的额外的编码向量，而不是整个消息，从而降低了加密容量，但增加了空间开销。

文中提出一种更加高效的防全局窃听者的方法，可以最小化空间开销和加密容量。方法的主要思想在于利用一些映射值生成一个源节点上的预编码矩阵，从而不需要额外的编码向量，达到降低加密容量和最小化空间开销的目的。

1 预备知识

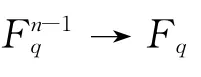
用一个无环有向图G＝（V，E）表示通信网络，其中V和E分别代表节点集和边集。每条边能够无差错地传送有限域Fq上的一个数据包，其中q为有限域的尺寸。源节点S希望将一个大的文件M发送给所有的接收节点，M被S分割为r个数据包。每个数据包用xi＝ （xi1，…，xin-1）∈Fn-1q表示，1≤i≤r，q＞r。

中间节点在Fq上为其收到的数据包随机选取编码系数，并将数据包的线性组合发送到每条出边上。信宿节点在收到至少r个线性独立数据包后，可以利用高斯消去法进行解码，从而得到M。假定网络中存在着一个全局窃听者，他的窃听能力不受限制，并且可以随意选择独立边，这也意味着被窃听边上的全局编码向量是相互独立的。

2 本文算法

2.1 源节点预编码

那么，利用这r个映射值h（xi），1≤i≤r，构造出如下的预编码矩阵P：

显然，P是一个范德蒙矩阵，且是一个可逆矩阵，因此可以用于源数据包x1，…，xr的预编码，预编码方式如下：

预编码后可得，然后源节点S将与相应的映射值h（xi）联接，得到一个预编码后的数据包

在这之后，S生成一个如下所示的扩展数据包：

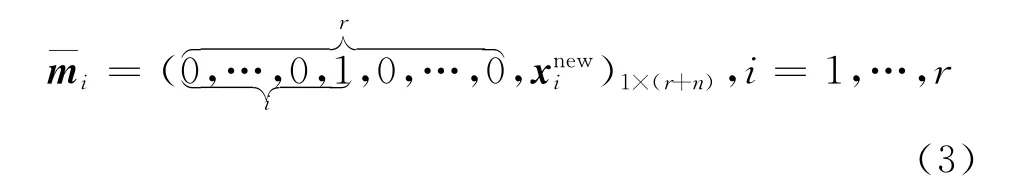
经过上述预编码步骤后，扩展数据包被发送到网络当中，且中间节点采用随机线性网络编码（RLNC）的编码方式。

2.2 信宿节点解码

当一个信宿节点接收到至少r个独立的消息数据包后，它可以根据如下步骤进行解码：

步骤2：对 ［xnew1，…，xnewr］T的最后一列解密，得到 ［x′1，…，x′r］T和h（xi）。

步骤3：利用h（xi），i＝1，…，r构造预编码矩阵P。计算出逆矩阵P-1并将h（xi）从 ［x′1，…，x′r］T中移除，得到 ［1，…，］T。

步骤4：最后，通过计算 ［x1，…，xr］T＝P-1·［1，…，］T，得到原始数据。

2.3 安全性分析

假设窃听者知道映射函数h（·）和矩阵P的构造特点，但是窃听者的计算能力有限，也就是说，如果给定一个映射值b，是不可能通过计算找到输入a使得h（a） ＝b。

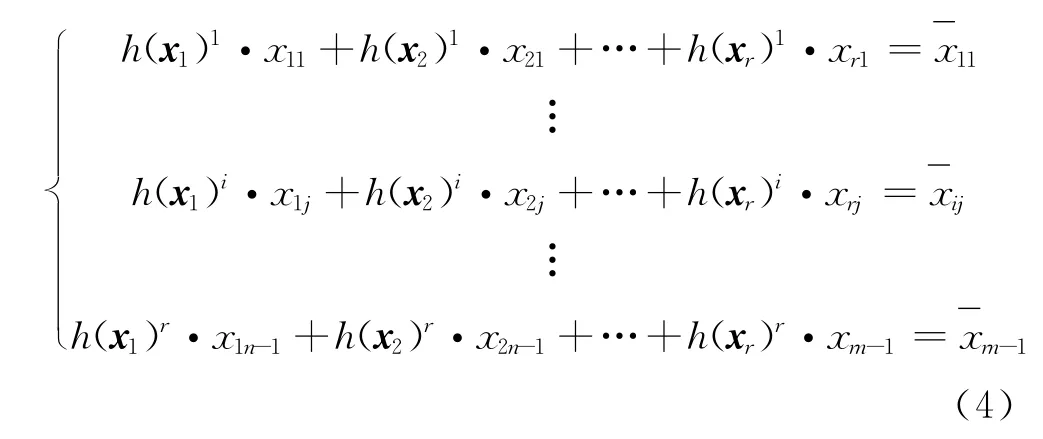
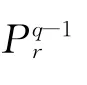
式中：YW为W上传输的数据包。

因此，在不知道 （h（x1），…，h（xr））的情况下，窃听者无法恢复（x1，…，xr），从而保证了原始数据包的安全性。

3 性能比较

考虑在尺寸为28的有限域上传送数据，单个数据的最大尺寸为1 500字节，信源节点由此产生200个被编码的数据包。1 500字节等价于F28上的1 500个符号。

3.1 空间开销

SPOC算法用r个r长的全局编码向量加密r个n-r长的原始数据包，这些全局编码向量被加密后放在相应的预编码数据包的包头，并称之为锁定系数。而本文算法中共有r个n-1长的原始数据包，经过预编码后得到n长的预编码数据包，这表明每个数据包的空间开销为1，预编码数据包的最后一个字符用于构造锁定系数，因此只需要加密这一个符号，也就是说空间开销和加密容量独立于数据包。

由于产生了200个被编码数据包，那么在SPOC算法中，每个被编码数据包上的锁定系数所占用的空间为200字节。而依据本文算法，无论传送多少个数据包，每个数据包上的锁定系数占用空间只有1个字节。那么SPOC和本文算法的空间开销比例分别为：

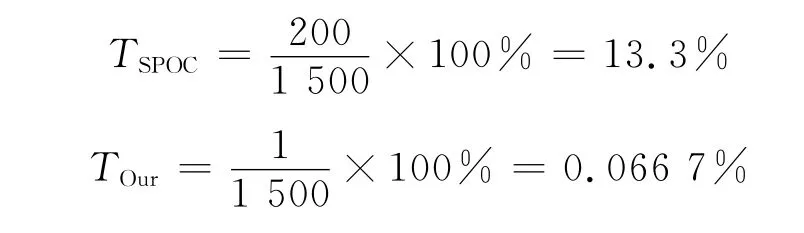
3.2 加密容量

加密容量Evol指的是应用算法传送数据的过程中，需要被加密的数据的尺寸大小。

如果用k表示数据包个数，Fmax表示单个数据包的最大尺寸，L表示被传送数据的总的尺寸大小，计算出有限域F28上，经典算法和文献［11］、［12］、［13］以及本文算法的加密容量表达式分别为：

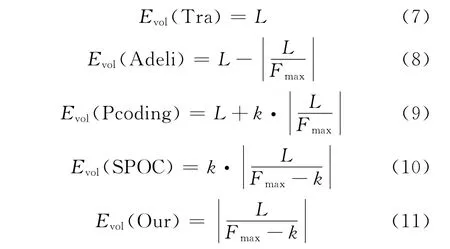
由此可得如图1所示的加密容量对比图。由图可知文献［12］的Pcoding算法产生的加密容量最大。而重合的2条曲线表明，文献［11］的Adeli算法和经典算法所产生的加密容量几乎相等。文献［13］的SPOC算法产生的加密容量则呈阶梯式增长。贴近x轴的曲线即为本文算法的结果，显然本文算法中的加密容量相比于其他算法得到了显著降低。

3.3 计算复杂度

图1 加密容量对比

文献［13］表明SPOC算法的计算复杂度为Ο（r3），其主要的计算代价集中在r×r维锁定系数矩阵的求逆和乘积运算中。文献［11］提出的算法的计算复杂度为Ο（r·n），计算代价集中在对每个数据包都要进行对应的Hash值的迭代计算。文献［12］中算法的计算复杂度为Ο（r），其计算代价在于对每个数据包进行置换加密。

在一个n长的数据包情况下，表1给出了本文算法与其他算法在加密容量、空间开销和计算复杂度之间的比较。从中可以看出本文算法所导致的空间开销和加密容量都非常小；另外，本文算法的计算复杂度与SPOC一样都是Ο（r3），计算代价主要由预编码矩阵P的求逆和其他矩阵运算构成。总而言之，文中算法是一种高效率算法，所要求的空间开销和加密容量都更小，并且计算复杂度也适中。

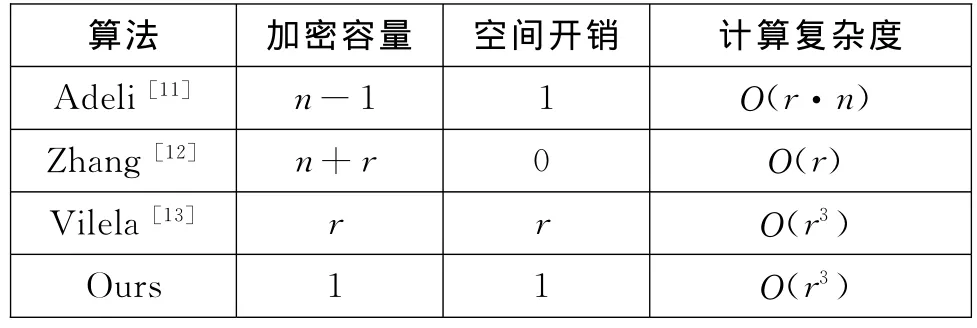
表1 算法的综合性能比较

4 结束语

本文基于计算安全，结合传统密码学方法提出一种增强型轻量级防窃听算法，算法的基本思想是利用与r个原始数据包对应的r个密钥生成一个范德蒙矩阵作为预编码矩阵用于随机化原始数据包。密钥加密后被放置在相应的预编码后的数据包的尾端，从而得到一个新的被发送到网络中的数据包。安全性能分析和数据对比表明，本文算法既达到了安全要求，同时也最小化了空间开销和加密容量。

［1］ Ahlswede R，Cai N，Li S-Y R，Yeung R W.Network information flow ［J］.IEEE Transactions on Information Theory，2000，46（4）：1204-1216.

［2］ Li S-Y R，Yeung R W，Cai N.Linear network coding［J］.IEEE Transactions on Information Theory，2003，49（2）：371-381.

［3］ Ho T，Medard M，Koetter R，et al.A random linear network coding approach to multicast ［J］.IEEE Transactions on Information Theory，2006，52（10）：4413-4430.

［4］ Cai N，Yeung R W.Secure network coding［A］.IEEE ISIT，2002［C］.Lausanne，Switzerland，2002：323.

［5］ Feldman J，Malkin T，Stein C，et al.On the capacity of secure network coding［A］.42nd Annual Allerton Conference Communication，Control and Computer［C］，2004.

［6］ Ngai C K，Yeung R W，Zhang Z.Network generalized hamming weight［A］.Netcod 2009 ［C］.Lausanne，Switzerland，2009：48-53.

［7］ Wei V K.Generalized hamming weight for linear codes［J］.IEEE Transactions on Information Theory，1991，37（5）：1412-1418.

［8］ Bhattad K，Narayanan K R.Weakly secure network coding［A］.Netcod 2005 ［C］.Riva del Garda，Italy，2005.

［9］ Harada K，Yamamoto H.Strongly secure linear network coding ［J］.IEICE Transactions on Fundamentals，2008，E91-A（10）：2720-2728.

［10］Silva D，Kschischang F R.Universal secure network coding via rank-metric codes ［J］.IEEE Transactions on Information Theory，2011，57（2）：1124-1135.

［11］Adeli M，Liu H P.Secure network coding with minimum overhead based on hash functions ［J］.IEEE Communications Letter，2009，13（12）：956-958.

［12］Zhang P，Jiang Y X，Lin C.P-coding：secure network coding against eavesdropping attacks［A］.IEEE INFOCOM，2010［C］.San Diego，CA，USA，2010：1-9.

［13］Vilela J P，Lima L，Barros J.Lightweight security for network coding［A］.IEEE ICC，2008［C］.Beijing，China，2008：1750-1754.