机构投资对我国资本市场资产价格影响的实证研究

陈 康

（浙江工商大学，浙江 杭州 310018）

一、问题提出

自夏普（William F.Sharpe，1964）提出资本资产定价模型（CAPM）开始，学者对于该模型在现实经济中的实证研究便从未间断。在国外，早期的实证结论基本都肯定了CAPM定价模型具有较强的解释能力。近些年随着机构投资者的快速发展，特别是共同基金的繁荣发展，大量学者又开始了对资本资产定价模型的实证研究，并得出不同的结论，这些研究大多质疑CAPM模型假设条件的合理性。在我国，由于经济发展较西方发达国家落后，20世纪90年代资本市场才逐步建立起来，致使经典CAPM模型的实证在我国股票市场上的解释效率较低。近年来，随着资本市场的不断成熟与完善，特别是1999年我国证监会明确了“超常规培育机构投资者”的政策导向，对机构投资者的快速发展有很强的推动作用，使我国机构投资者持股市值比重大幅增加。首先，从积极的角度来看，与个人投资者相比，由于其规模化的经营，机构投资者参与上市公司治理的成本远远小于一般个人投资者，那么机构投资者更有积极性参与公司的决策和治理；从消极的角度来说，这也给机构投资者提供了与上市公司进行合谋的机会，合谋的结果必然是机构投资者与上市公司共同侵占中小投资者的利益。其次，机构投资者拥有更多的信息优势。从积极的角度看，机构投资者的高效信息获取能力对提高资本市场的效率起到了积极推动作用；从消极的角度看，由于金融市场制度尚不完善和监管不力，机构投资者往往有机会通过非法手段获取内幕信息，从而牟取非法利益。那么，机构投资者的存在和发展对我国资本市场资产价格究竟是何种影响呢？本文基于这样的考虑，尝试将经典CAPM模型改进，找出更加适合我国资本市场的定价模型，旨在探求机构投资者对我国资本市场资产价格的影响。

表1：数据来源和描述

二、机构投资对资产价格影响的实证分析

在20世纪90年代，也就是我国资本市场刚刚起步阶段，我国股市在大量的个人投资者的见证中经历了几次大起大落，股票市场极不完善，资本资产价格严重偏离其本身的价值。21世纪以来，随着机构投资者的不断发展，其已经成为资本市场非常重要的投资者，其投资偏向和资产配置影响着市场中的个人投资者。机构投资者不同于自然人，他们以法人的身份在市场中交易股票、债券等证券及证券衍生品。在美国、英国，机构投资者为保险基金、养老基金、共同基金，他们对上市公司的持股稳步增加，主导着资本市场的发展；在日本，最常见的是法人机构相互持股，但其本质仍然是机构在主导着市场。随着我国经济的发展和对外开放程度的不断深化，资本市场的发展也日益离不开机构投资者。现如今，我国机构投资者日益发展壮大，持股比例也是逐年上升，机构投资者主要有社保基金、证券投资基金、保险公司等。由于机构投资者具有专家理财、分散风险等作用，他们的存在对资本市场的资产价格有着深远的影响，本文在经典CAPM模型基础上引入机构投资者的影响，从而分析机构投资者对股票价格的影响。

（一）数据描述及变量定义

搜集1999年3月到2011年3月间上海证券交易所A股主板上市公司的股票收益率，剔除ST、*ST等股票，将1990年12月19日到1999年2月28日在上交所正常上市的股票筛选出来，这是为了保证在1999年3月到2011年3月收益率数据的完整性。同时剔除在1999年到2011年内退市的股票，最终得到303只上市股票。模型中个股数据采用月收益率Rit，共12年零1个月，即145个月。由于我国资本市场发展时间较短，市场组合的选取较为困难，上证综合指数（000001）是上海证券交易所编制的，以在上海证券交易所挂牌的所有股票为计算对象，计算方法采用加权平均，权数为各股票的发行数量。由于涉及的股票全面，上证综指基本反映了整个证券交易市场的总体走势，可以作为资产定价模型中的市场组合。所以，搜集2006年1月到2011年3月的上证综指月收益率，共计63个月。无风险收益率Rf在这里我们采用居民3个月定期存款利率R3m计算。

关于机构投资者的投资偏好研究中，巴德里纳特等（Badrinath等，1989）最早提出机构投资者的“审慎人假说”，他们指出共同基金、养老基金等机构投资者需要承担受托责任，在投资中应该“审慎”地行事，具体而言美国机构投资者偏好于投资资产规模大、超额回报率高、β值大、流动性强、获得S&P高评级、上市时间长的股票，避免持有收益率波动性高的股票。埃金斯（Eakins，1998）和皮努克（Pinnuck，2004）分别在美国资本市场和澳大利亚资本市场得到了类似的结论，进一步证实了机构投资者的“审慎人假说”。机构投资者的行业配置研究尚未形成统一的成果，不同的机构投资者采用不同的行业配置方法进行资产组合，其中在实践部门中最具代表性的为高盛的Blaek-Litterman行业配置模型和美林的投资时钟（InvestmentClock）行业配置模型。Blaek-Litterman行业配置模型是一种资产的期望收益等于市场均衡收益和投资者主观预期收益的加权平均，陈越强（2010）就采用了这一模型构建了投资组合，研究表明运用这种方式进行投资组合能够获得相对于市场均衡收益更高的回报。投资时钟模型是根据宏观经济周期的不同阶段来研究行业配置的顺序和行业相关程度。

遵循上述有关机构投资者投资策略的研究，并根据实践部门中机构投资者会通过行业配置来进行资产组合的思想，本文将行业分为28个大类，它们分别为电子通讯、科技行业、纺织行业、钢铁行业、汽车行业、医药行业、化工行业、机场港口、公路桥梁、玻璃行业、商业行业、电力行业、发电设备、交通运输、房地产业、家电行业、节能环保、农药化肥、造纸行业、金融行业、机械制造、水泥行业、煤炭行业、3G概念、有色金属、食品行业、基础材料、白酒红酒。在这28个行业中，根据机构投资者的审慎投资原则筛选出各行业的相关股票，这些股票具有资产规模大、β值大、流动性强、高评级、上市时间长和收益率波动性小等特点，能够较好地反映机构投资者的投资偏好。最终，共筛选出49只具有行业代表性并受到机构投资者青睐的股票，并把这一投资资产组合定义为基准投资组合。

（二）模型设计

假设市场只存在两类投资者，一类代表个人投资者，另一类代表机构投资者，他们均是相互独立决策风险厌恶者，对于机构投资者而言，投资经理或投资团队的报酬与他们投资组合的绩效有关，经理会以其投资获取最大的超额绩效作为目标。假定市场中某投资机构i（i=1，2，…，I）采用投资组合的方式来分散风险，采用第i种的基准组合作为参考，对于投资机构的投资组合而言，其选定的基准投资组合的组成股票投资值占投资组合总额的百分比写作向量形式xoi，相应地有j'xoi=1，j是单位列向量。市场的资产收益服从多元正态分布（μ，Ω），μ为n×1阶的列向量，Ω则是n阶的矩阵。对于所有机构投资者而言，存在向量组X，对于单个机构投资者而言，实现自身的报酬最大化，用均值方差模型描述，可以表述为：

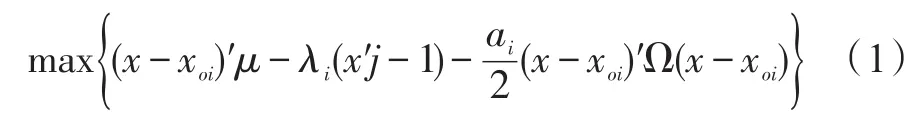
根据布伦南和李菲菲（Michael J.Brennan和Feifei Li，2008）的推导思路，最后推导出CAPM扩展模型为：

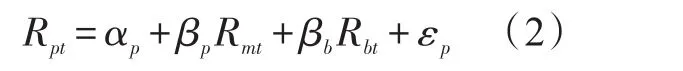
式中Rpt为资产组合收益率，Rmt为市场组合收益率，Rbt为机构投资者的基准投资组合收益率，βp为资产组合的系统风险测度，βb为基准投资组合的系统风险测度。

同样，搜集属于基准投资组合的上述49只股票从2006年1月到2011年3月的月收益率数据，并计算投资组合收益率。组合收益率等于这49只股票个股收益率加权平均数，这里，我们假设整个市场的机构投资者对上述股票进行等比例投资，则组合收益率等于单只股票收益率的算数平均数。由于整个市场的机构投资者持股基本都集中在各行业的龙头股，所以这样的假设基本能够反映机构投资者的投资偏好。

（三）实证研究

为了较好地确定资产组合，计算样本数据中单只股票β值，将β值按照升序排序，从而将303只股票分为10个组合，其中第一组到第七组股票数均为30个，第八组到第十组股票数则为31个，最后计算出十组资产组合从2006年1月到2011年3月的月收益率。

采用F-M（Fama-Macbeth）检验方法，对（2）式进行时间序列回归分析，对10组资产组合分别进行模型回归，根据模型的回归结果进行模型检验。

首先，异方差性检验。利用White检验方法进行检验，因为各组White检验结果相似，所以以第一组资产组合为例。第一组资产组合的White检验结果如表2所示。

由表2可知，nR2=2.758462，查x2分布表后，得到临界值（2） =5.991，因为nR2＜5.991，所以认为模型不存在异方差性（也可通过p值判断得到结论，p=0.7372）。扩展模型消除了过去经典CAPM实证中存在的异方差性，模型得到了改善。

其次，自相关性检验。利用Durbin-Watson（DW）检验方法，根据模型回归结果，将各组资产组合模型的DW值整理得到表3。

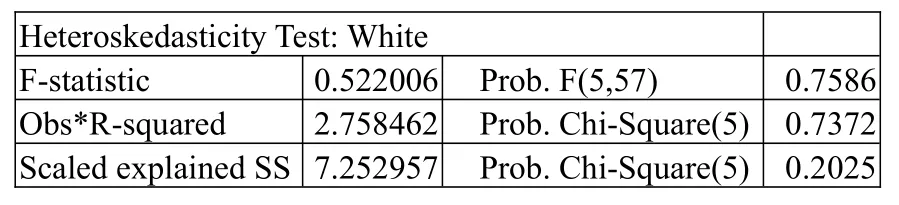
表2：第一组资产组合的White检验结果

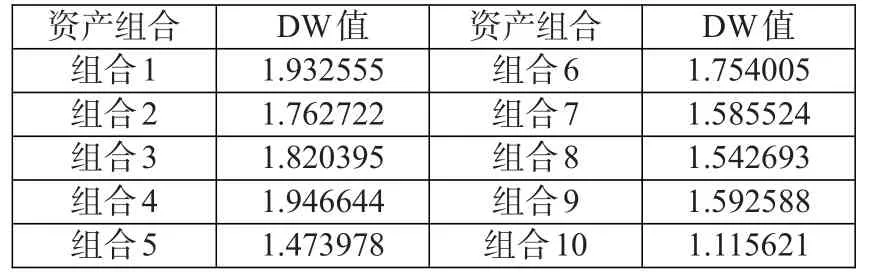
表3：模型DW值

由表3可知，各资产组合模型中的DW值大部分都较接近2，所以基本可以判断模型不存在一阶自相关性。

最后，多重共线性检验。采用相关系数法检验解释变量之间的相关情况，得到Rmt与Rbt的相关系数为0.91848，较高，说明解释变量存在一定的线性相关性。

由于模型不存在异方差性和自相关性，所以可以使用普通最小二乘法进行回归并进行经济检验和统计检验。

1.经济检验。根据模型回归分析结果，整理出模型的双贝塔值，如表4所示。

从表4中可以看出，除组合5的 βp值为正数以外，其他9组资产组合的 βp值均为负数，取其平均值为-0.1559084，说明资产组合的收益率与市场组合收益率成反比，比例系数约为0.16，即市场组合收益率每变动1个单位，资产组合收益率随之向相反方向变动0.16个单位左右。再看新引入的 βb值，各组的βb值十分接近，取其平均值为1.2415516，说明资产组合的收益率与基准组合收益率成正比，比例系数约为1.24，即基准投资组合收益率每变动1个单位，资产组合收益率随之向相同的方向变动1.24个单位左右。

表4：双贝塔值（βp、βb）

2.统计检验。首先，进行拟合度检验。根据模型回归分析结果，整理出模型的拟合度判定系数，如表5所示。

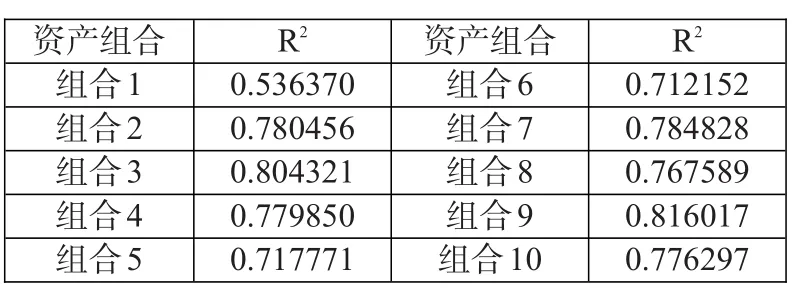
表5：模型拟合度判定系数（R2）

从表5可知，模型拟合度判定系数取上述各判定系数的平均值0.7475651，即R2=0.7475651，在金融领域实证中拟合程度较高。扩展模型中，Rˉ2值与R2值非常接近，都超过了过去经典CAPM实证结果中的拟合程度，所以，模型拟合度得到了很大的改善。

其次，进行模型的显著性检验。显著性检验过程通常采用数理统计中的假设检验方法。对模型进行显著性检验时，利用F统计量检验。各组资产组合F统计量及伴随概率整理后如表6所示。

表6：模型F统计量及伴随概率

从表6可知，除组合1以外，其余各组资产组合F统计量均超过74，模型的F统计量取组合2—9的F统计量平均值103.6020556，查F分布表得到临界值F0.05（1，F0.5（1.61））=4.00，模型的F统计量远大于临界值，则拒绝原假设（H0∶βp=0，βb=0），所以，βp≠0，即模型通过显著性检验。且其伴随概率Prob（F-statistic）=0，说明拒绝原假设正确的概率为100%。

最后，进行解释变量的显著性检验。这时，模型变成了二元线性回归模型，不同于一元线性回归模型，方差的总体线性关系是显著的，不能说明其中的解释变量对被解释变量的影响是显著的。所以，这里，还需继续进行解释变量的显著性检验。

采用t统计量进行检验。模型的t统计量整理后如表7所示。

表7：解释变量Rmt、Rbt的t统计量

给定一个显著性水平α=0.05，n=63，k=2，查t分布表得到t0.025（t0.025（60））=2.00。由表7可知，模型的解释变量Rmt的t统计量均小于2，而且有9个资产组合小于零。解释变量Rbt的t统计量均大于2。所以，Rmt这个解释变量不能通过显著性检验，而Rbt通过显著性检验。在之前的多重共线性检验中，我们得到模型存在共线性，多重共线性的存在会影响t检验的可靠性，使得系数估计误差增大，从而导致t统计量减小，这也就是为什么在经典CAPM实证中Rmt能够通过显著性检验，而在这里无法通过显著性检验的根本原因。

三、结论及建议

加入机构投资者影响的CAPM扩展模型，消除了经典CAPM模型中存在的异方差性，且不存在一阶自相关性。模型在经济检验中，得到资产组合的收益率同市场组合收益率呈反比关系、与基准投资组合收益率呈正比关系的结论。在拟合度检验中，模型拟合度有了很大的改善。在解释变量的显著性检验中，Rbt通过显著性检验，而Rmt未通过显著性检验，模型存在多重共线性是其无法通过显著性检验的根本原因。通过本文的分析，机构投资者将能够对我国资本市场资产价格产生一定的影响。

我国股票市场起步于个人投资者，个人投资者又具有较多的投机行为，而成熟的机构投资者试图使得资产价格逐步回归合理，并改善市场的投机行为，对股票市场的发展将起到稳定和推动的作用，并促进经济繁荣。由此，我们提出的政策建议是资本市场应该大力发展机构投资者，机构投资者本身也应该朝着健康的方向发展。

[1]Eugene F.Fama，Kenneth R.French.1992.The crosssection of expected stock returns[J].The Journal of Finance，47（2）.

[2]Zakri Y.Bello.2008.A statisitical comparison of the CAPM to the Fama-French three factor model and the Cahart's model[J].Global Journal of Finance and Banking Issues，2（2）.

[3]Muhammad Hanif，Abubakar Javaid Dar.Comparative Testing of Capital Asset Pricing Model（CAPM）and Shari'a Compliant Asset Pricing Model（SCAPM）：Evidence from Karachi Stock Exchange-Pakistan[J].Middle Eastern Journalof Scientific Research，Forthcoming