中国财政周期波动的非对称性特征研究
孙晓娟
(厦门理工学院 商学院,福建 厦门 361024)
一、经济周期非对称的类型
所谓经济周期非对称,简单地说,即是指扩张与收缩的镜像不能重合,或者说是扩张与收缩的程度和轨迹不同(正常的对称性周期波形的镜像都是重合的,如图1(a)所示)。实际上,早在1927年和1936年时,米斯塞尔(Mithcell)和凯恩斯(Keynes)等学者就分别对经济周期的非对称性进行了描述和提及[1]。例如,凯恩斯认为经济周期向下收缩时的程度较剧烈,或者说陡峭,而扩张时向上的趋势却较缓和。之后,许多学者对经济周期的非对称进行了研究,得出了一系列重要的结论。这其中最重要的,是对经济周期非对称类型的界定。而对非对称类型的定义和分类中,最典型的是西歇尔(Sichel)[2]于1993年对经济周期给出的两种分类。西歇尔认为经济周期非对称可以分成陡度型非对称和深度型非对称,并给出了严格的定义。他认为陡度型非对称是指扩张与收缩的斜率不同,因此根据扩张与收缩斜率的差异,经济周期的非对称又可分成陡升缓降型和缓升陡降型两种类型(如图1(b)、(c)所示)。其次,深度型非对称是指扩张期间和收缩期间的振幅不同,或者说是波峰和波谷偏离趋势值的距离不同,例如假如波谷偏离趋势值的距离更大,则称为收缩深度型非对称(如图1(d)所示)。陡度型非对称和深度型非对称并不是绝对独立的,二者可以同时存在,例如一个波形可以既是陡度型非对称也可以是深度型非对称(如图1(e)所示)。在深度型非对称和陡度型非对称的基础上,麦奎因和索利(McQueen and Thorley,1993)进一步提出了尖度型非对称(sharpness asymmetry),他们通过比较波峰和波谷的曲率的差异来定义非对称性。例如,从扩张到收缩时的变化大,而从收缩到扩张时的变化要相对小些,则可以称为扩张尖度型非对称,相反则可以称为收缩尖度型非对称。比如图1(d)同时也是一种收缩尖度型非对称。

图1 经济周期非对称类型
在对经济周期的类型进行简单介绍之后,本文在此基础上,将从以上三种类型分别对中国财政收入和支出的周期性特征进行检验,以分析中国财政周期性波动是否存在非对称特征。
二、中国财政周期波动的深度型非对称特征检验
考虑到财政方面的数据主要包括财政收入和财政支出两大类(下面对该两项指标的总值分别简称为yt和zt,其增长率序列分别简称为Δyt和Δzt),因此下面将分别以该两种指标进行检验。数据来源于《中国统计年鉴2012》。
具体步骤:先求出财政收入和财政支出波动的趋势值,然后再求出二者的波动指标序列,接下来再对波动序列的波峰值和波谷值进行比较,看是否存在明显的非对称特征。
使用Eviews软件,运用HP滤波法先求出中国财政收入的趋势值,再用财政收入的实际增长率减去其趋势值,得到该指标的波动指标序列如图2所示。直观地看,中国财政收入的波动序列的波动频率还较高,在1978~2011年一共出现过7次波动(同期的国内生产总值共出现过6次波动),波动频率达到了0.2,波动幅度也较大,平均值达到了18%,远高于国内生产总值的波动幅度(5.4%)。再者,从波形上看,似乎波峰值要比波谷值的绝对值更大一些,因此为了更加确切地验证峰谷偏离趋势值的距离,下面用“谷—谷”法对中国财政收入的周期进行划分[3],列出每一轮周期的峰值和谷值,在此基础上,再对其波动序列的峰谷绝对值进行比较。

图2 财政收入HP滤波趋势值及波动序列
中国财政收入的周期划分及其峰谷值计算结果于表1所示。
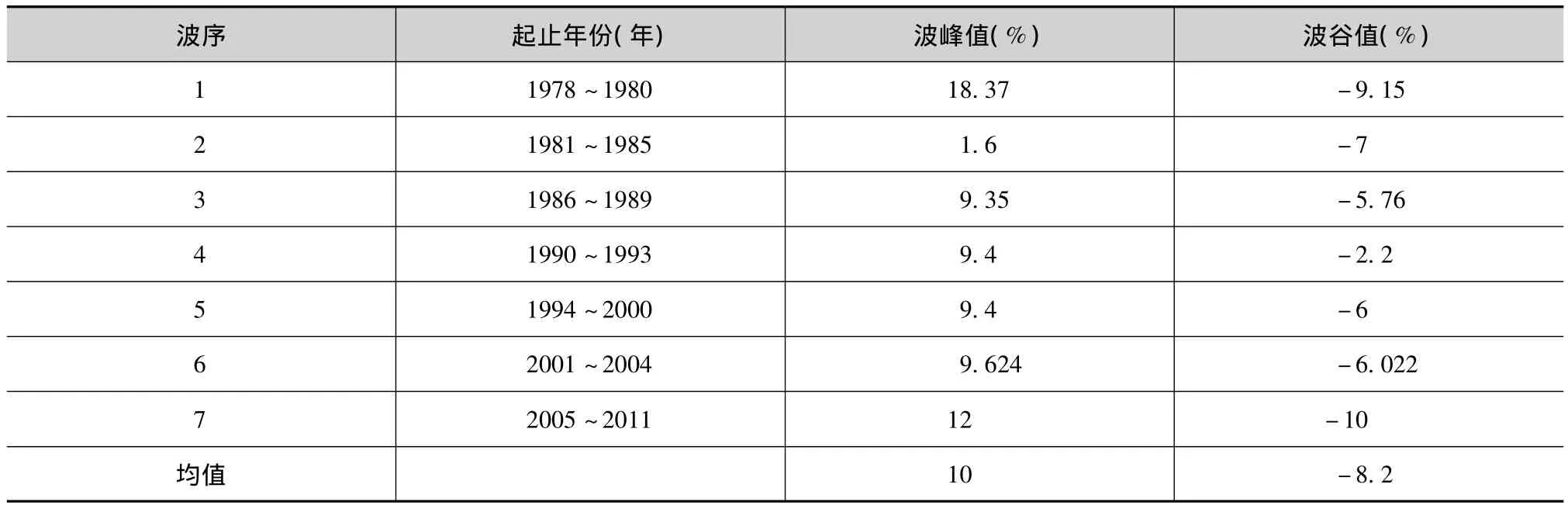
表1 中国历轮财政收入周期的峰值与谷值计算
由表1可知,除了第二轮周期之外,其余周期的波峰绝对值显著大于波谷的绝对值,说明波峰偏离趋势值的距离比波谷要大。
再来看财政支出的HP趋势值及其波动序列,如图3所示,由其可知,中国财政支出一共呈现出5个周期,其波动频率比财政收入要稍小,但是其波动幅度也达到了16%,虽比财政收入要略微小些,但是却也是远远高于国内生产总值的波动幅度,通过与财政收入同样的方法,也可计算出财政支出的周期划分及其峰值和谷值如表2所示。

图3 财政支出HP滤波趋势值及波动序列

表2 财政支出历轮周期波峰与波谷值计算
由表2可知,财政支出的波峰与波谷的绝对值也是呈现出与财政收入相同的结果,即波峰偏离趋势的距离要更大。
通过对财政收入和财政支出的峰谷偏离度的计算,可以初步得知中国财政周期在扩张时与收缩时的镜像不重合,而且波动呈现出显著的扩张式的深度型非对称[4]。
三、中国财政周期波动的陡度型非对称特征检验
接下来本文运用BK模型法对中国财政周期的陡度型非对称进行检验。BK模型是博德里(Beaudry)和库普(Koop)于1993年创立的,其主要思想是:由于经济周期的非对称性,因此在构造经济周期的模型时必须引入非对称项和非线性成分,BK模型主要是一个基于ARMA模型的表达式[5],具体如下:

(2)式主要是引入了非对称项εt,系数K(L)和M(L)都是滞后L阶的滞后算子多项式,其中St是时间序列中yt的衰退程度变量,其最大滞后项为n,故 (2)式是一个包含衰退变量的ARMA(p,q)模型。那么 (2)式是否包含了非对称的含义呢?再对 (2)进行简化分析。先假设两个滞后算子K(L)和M(L)都等于1,而衰退变量只有一项,那么 (2)式则变成了 (3)式:

如 (3)式中的β值不等于零,那么该序列就会产生非对称性,例如假如β值大于零,当εt-1小于零时,序列yt出现收缩时,其受到的冲击就会使其实际值低于其趋势值Δyt=α+β1St-1,而此时的衰退变量并没有发生变化,因此反向冲击的持续作用比正向冲击εt大于零的时候要小一些,而当εt-1大于零时则会相反,由此原时间序列yt和其增长率序列Δyt都会出现非对称性[6]。
关于衰退变量St,一般来说包括平均衰退变量、绝对衰退变量和门限衰退变量,由于绝对衰退变量和平均衰退变量都容易造成过长和过久的记忆,因此本文采用门限衰退变量来进行实证检验。
门限衰退变量实际上是每一轮周期的峰值与该周期内每年的实际增长率的差值,假如某个周期内的峰值为m2t,而实际增长率为Δyt,那么衰退变量St=mt-Δyt,从而可计算出历轮周期的衰退变量。因此可利用“谷—谷”法得出历轮财政收入和财政支出周期中的门限峰值如表3和表4所示 (由于本文是采用的财政收入增长率指标,因此周期划分与表1的计算结果有所不同)。然后再求其与实际增长率的差值,可得门限衰退变量的曲线如图4和图5所示。

表3 财政收入周期波动中的门限峰值

表4 财政支出周期波动中的门限峰值

图4 中国财政收入波动的门限衰退变量

图5 中国财政支出波动的门限衰退变量
由图4和图5可知,中国不论是财政收入还是财政支出,其门限衰退变量都是在改革开放初期的时候衰退程度较大,随着改革的深入,其衰退程度逐渐减弱。这说明随着中国宏观经济的稳定,财政收入得到了强有力的保障,因此使得收入和支出都得到了相当程度的增长,财政的抗衰退能力也越来越强[7]。
在构建完两个财政指标的衰退变量之后,再来建立门限衰退变量以及财政收入和支出的滞后项的BK模型。这里的BK模型是采用ARMA模型的形式来建立的[8],因此首先需要确定ARMA模型的滞后项。通过EVIEWS软件求二者的自相关系数和偏相关系数得知,他们都是在4阶时出现截尾,并且衰退变量的滞后项为4时BK模型是最优模型,所以本文选择ARMA(4,4)模型和n=4。首先,建立财政收入的BK模型:

其次,财政支出的BK模型如 (5)式所示:

由 (4)式和 (5)可知,两个回归式的拟合度都较高,说明其回归结果较理想。不论是财政收入还是财政支出,都是一阶滞后项的门限衰退变量的t统计值显著,这说明本文构造的门限衰退变量能在相当程度上解释中国财政收入和财政支出,并且表明中国的财政周期波动存在基于门限衰退变量的非对称,其波动曲线图的扩张与收缩的影像不重合。
再者,从上面两个回归式可以看出,一阶滞后项的门限衰退变量的系数都是大于零的,说明在中国财政波动中,其所受到的正向冲击比反向冲击要大,结果是上升较下降要急促,也就是说,中国的财政波动是属于扩张型的陡度非对称[9]。
四、中国财政周期波动的尖度型非对称特征检验
将以二阶导数作为分析工具,对中国财政周期的尖度型非对称性进行检验。由于尖度型非对称是比较峰谷增长率的变化率,而该变化率又可以用增长率的导数 (即总值的二阶导数)来表征,因此本文将计算出财政收入和支出每一轮周期的波峰和波谷增长率的导数,然后再对二者进行比较,即可检验出财政波动是否存在尖度型非对称[10]。首先介绍二阶导数方法:
用gt来 表示第t 年的财政收入增长率,则其中,
在年度时间序列数据中的Δt都是1,因此可以近似得到下式:

由 (6)式可知,可以用相邻两年增长率的差来度量收入波动的变化,假设收入的波峰年份为第t年,那么波峰值的变化率则为Δ=gt-1-gt。如Δ的绝对值大则表明增长率变动剧烈。再根据 (6)式,还可计算出历年财政收入和支出的二阶导数值如图6所示,该图表明,中国财政总值的二阶导数曲线越来越趋向于平缓,说明财政波动曲线越来越平滑。
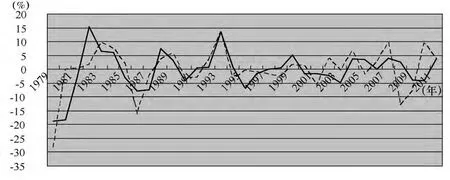
图6 中国财政收入和支出的二阶导数曲线
最后根据表3和表4的周期划分结果,可计算出财政收入和支出的历轮周期的波峰值和波谷值的导数值 (如表5和表6所示)。

表5 基于波峰和波谷年份的我国财政收入的二阶导数值 (%)

表6 基于波峰和波谷年份的中国财政支出的二阶导数值 (%)
由表5和表6可知,不论是收入还是支出,其波峰年份的二阶导数值的绝对值都要显著大于波谷年份的导数值。说明波峰时的曲率要比波谷时的曲率尖耸,至少在该样本期内,可以认为中国的财政波动应该是呈现出扩张尖度型的非对称[11]。
综上所述,本文通过HP滤波法、BK模型估计和二阶导数法,有力地证明了中国财政周期波动存在着显著的深度型、陡度型和尖度型非对称,说明不论是财政收入还是财政支出,都是扩张时期受到的冲击较收缩时要大,因此波峰的偏离度要比波谷高。
五、总结
财政收入和财政支出是宏观经济的重要组成部分,该两项指标的波动规律的分析对于中国宏观经济的稳定有着重要意义。因此本文以收入和支出为例,对中国的财政周期波动的非对称性特征进行了分析,本文的实证分析得出了一系列有意义的结论。经济周期非对称主要分为深度型、陡度型和尖度型。本文分别从这三种类型的角度对中国财政波动进行了检验。从深度型的角度来看,先通过HP滤波计算出收入和支出的趋势值,然后通过比较,可知收入和支出两项指标的峰值都要大于谷值的绝对值,因此可以认为二者都存在深度型非对称;其次通过BK模型法得知,门限衰退变量的一阶滞后系数显著大于零,这不仅表明中国财政收入和支出存在显著的非对称,而且可以证明其所受到的正向冲击要大于负向冲击,因此有力的证明了财政周期波动存在扩张陡度型非对称;再从尖度型的角度来看,通过求峰谷年份的二阶导数值的方法,得知收入和支出都存在一个显著的特点,即波峰年份的增长率变化值 (即总值的二阶导数值)的绝对值都要明显大于波谷年份的变化值,表明由扩张向收缩转换的概率要大于由收缩向扩张转换的概率,这与国外学者对尖度型非对称的定义是一致的。
通过综合分析,本文认为中国财政波动存在扩张深度型、陡度型和尖度型相结合的非对称特征。该项结论对于中国的宏观调控有着重要的启示。首先财政波动的扩张深度型非对称特征表明,财政收入和支出在扩张期的迅速增长是中国经济过热的重要原因,因此中国的宏观调控的着力点应该主要致力于扩张时期,尤其在经济扩张时,要警惕中国的财政支出过快增长,建立起财政支出的监控和预警机制;其次尖度型非对称的分析结论表明,在经济繁荣时期,必须防止中国财政收入的急剧滑坡,要采取措施保持财政收入的稳定增长。
[1]刘金全,刘志刚,于冬.我国经济周期波动性与阶段性之间关联的非对称性检验——Plucking模型对中国经济的实证研究[J].统计研究,2005,(8):8-12.
[2]Sichel D E.Business Cycle Asymmetry:A Deeper Look[J].Economic Inquiry,1993,(31):224-236.
[3]刘金全.中国实际GDP序列的非对称性度量和统计检验[J].财经研究,2002,(1):80-86.
[4]陈浪南,刘宏伟.我国经济周期波动的非对称性和持续性研究[J].经济研究,2007,(4):43-52.
[5]Bachmeier Griffin.New Evidence on Asymmetric Gasoline Price Responses[J].Review of Economics and Statistics,2003,22(3):43-67.
[6]张欣.崔日明基于非对称随机波动模型的人民币汇率波动特征研究[J].国际金融研究,2013,(1):66-68.
[7]万解秋,徐涛.政府支出、财政扩张与货币政策效率[J].财贸经济,2001,(2):75-79.
[8]Nicolas E Magud.On Asymmetric Business Cycles and the Effectiveness of Counter-Cyclical Fiscal Policies[J].Journal of Macroeconomics,2008,30(3):53-62.
[9]Khurshid M,Kian I.Detecting Business Cycle Asymmetries Using Artificial Neural Networks and Time Series Models[J].Computational Economics,2005,26(3):56-62.
[10]陈宇峰,陈启清.国际油价冲击与中国宏观经济波动的非对称时段效应:1978-2007[J].金融研究,2011,(5):60-66.
[11]李想,穆月英,郑丽琳.粮食价格波动对物价水平的非对称影响——基于STR模型的实证分析[J].统计与信息论坛,2012,(7):30-36.

