基于趋同性及ON/OFF的网络流量建模研究

高波，王昌伟，段虎

（1.深圳信息职业技术学院信息技术研究所，广东 深圳 518172；2.深圳信息职业技术学院计算机学院，广东 深圳 518172）

【信息技术理论研究】

基于趋同性及ON/OFF的网络流量建模研究

高波1，王昌伟1，段虎2

（1.深圳信息职业技术学院信息技术研究所，广东 深圳 518172；2.深圳信息职业技术学院计算机学院，广东 深圳 518172）

基于网络行为趋同性及ON/OFF模型，提出了一种改进的数据网络流量模型C-ON/OFF。通过理论分析及仿真实验，研究了C-ON/OFF模型中两个具有物理意义的参数（N和n）与生成流量归一化自协方差之间的关系。相比于其他模型，C-ON/OFF模型具有结构简单、计算复杂度低、物理意义明确等优点。

趋同性；长相关性；网络流量建模

1 引言

网络流量融合了网络运营时所有的信息，是最基础也是最关键的测量数据，因此对网络流量数据的分析与研究格外重要。随着物联网、泛在网络等概念的提出，下一代互联网骨干网各节点之间、局域网各节点之间的网络流量数据将呈现大幅度增长，互联网流量已迈入大数据时代。在大数据流量背景下，网络业务类别的急剧增加导致网络流量性质发生改变，传统的流量模型已不适用于当今乃至下一代互联网流量的分析与预测，因此对网络流量建模的研究势在必行。

20世纪90年代以前，数据网络的用户数量相比于传统电话网络的用户数量几乎可以忽略不计，数据网络的流量性质并未得到运营商、电信公司以及科研人员的关注，大多数人认为数据网络与传统电话网络的流量性质是一致的。但在1994年，Leland[1]等人指出，数据网络流量的特性与传统电话网络流量的特性有很大的差异——传统电话网络流量的自相关函数随时间间隔的增大呈负指数衰减，而数据网络流量的自相关函数的衰减速度明显慢于传统电话网络，与双曲函数的衰减速度类似。流量数据自相关函数的过慢衰减导致数据网络流量不同时间点的流量值之间的时间相关性始终存在，即使时间间隔足够大，这种相关性也不可忽略。这种特殊性质造成了如下后果：数据网络排队队列长度的衰减速度比按照Poisson模型和Markov模型估计出的结果慢得多，导致缓冲区溢出现象明显。这意味着，按照Poisson模型或Markov模型设计的数据网络，当用户数量达到一定规模后，在实际运营中会出现丢包率上升、时延增大的现象，严重恶化网络服务质量。

传统电话网络流量数据自相关函数的快速衰减特性被称为短时相关性（又称短相关，Short Range Dependence，SRD），而数据网络流量数据自相关函数的慢衰减现象被称为流量的长程相关性（又称长相关性，Long Range Dependence，LRD）。给出短相关随机过程和长相关随机过程的数学定义：某均值为零的随机过程，若其自相关函数r(k)满足式（1），则称该随机过程为短相关过程；若其自相关函数满足式（2），则称该随机过程为长相关过程。

其中，k代表时间间隔。联系到前文的自相关函数衰减现象，式(1)中r(k)的绝对收敛表明短相关过程的r(k)衰减速度应快于负指数函数的f(k)=k-1衰减速度；同理，式(2)代表的长相关过程r(k)的衰减速度应等于或慢于f(k)=k-1的衰减速度。因此，本文通过比较r(k)的衰减速度来判断流量数据是否具有长相关性。

另一种判断LRD的方式依靠Hurst参数值[2]。若某随机过程的Hurst参数值位于区间(0.5,1)时，则该随机过程具有长相关性；若其Hurst参数值位于区间(0,0.5)时，则该随机过程是短相关的。

20世纪末期，大多数网络流量建模的思路主要集中于找到刻画长相关性的数学工具，由此出现了很多长相关模型，例如FBM模型[2]、基于重尾分布的ON/OFF模型[3-5]、FARIMA模型[6,7]等；进入21世纪后，一些学者将人工神经网络[8,9]用于网络流量的建模，依靠智能算法强大的非线性能力来拟合长相关流量数据；目前，研究人员又将目光聚焦于混合模型[10,11]的建立，即将以上模型中的两种（甚至更多）结合在一起，优势互补，调和模型复杂度与准确度之间的矛盾。这些模型对于长相关性质的描述能力基本相当，不足之处在于：模型建立的时间成本较高（高计算复杂度）。

除以上方法外，将短相关模型加以改进，使之能够拟合长相关性质的流量模型开始涌现，例如文献[12]给出了一种新的拟合算法，将经典短相关模型ARMA转化为长相关模型，不但降低了系统复杂度，而且为长相关流量模型的研究开辟了新思路。但该系统模型参数仅能凭经验设置（参数不具备物理意义），模型的普适性较差。

综上所述，为适应大数据背景下的Internet骨干网流量特性，为网络的设计、管理、运营、计费提供技术参考和模拟数据，建立一个结构简单、计算复杂度低、具备一定物理意义的网络流量模型是十分必要的。

2 网络趋同性现象

随着Internet网络的普及、网络多媒体业务的快速增长、社交类网络的兴起，出现了这样的情形：年龄、兴趣、职业等等方面相近的人们对相同的热点事件或热门新闻的关注程度具有一致性，并且这些人对事件、新闻的关注会持续较长时间，直到下一个值得关注的事件或新闻的出现。这种特殊现象就是在当前各领域中经常提及的趋同性：一些互相协作的个体为了完成某个任务或者达到某种共同的目的，需要在某个都感兴趣的问题上达成一致。上文提到的“人们”就是这些互相协作的个体，这些个体的兴趣在于对新鲜事物的好奇，在于对事件的关注和评论，在于对新闻的传播和分享等等。趋同性现象已存在于自然界和很多应用研究领域，例如分布式计算[13]，协同控制[14]等等。

在网络研究领域，同一局域网内的用户（例如在某住宅小区、某所大学、某家企业居住、求学、工作的人们），他们的网络行为相似甚至相同，使得趋同性的现象更加明显，并且经常发生这样的情形：众多用户近乎同时的突然做出相同的网络行为。这些因素导致了局域网的网络业务流量之间产生了较大的相关性和较大的突发性。因此，以往的ON/OFF模型中对于各个ON/OFF源之间独立同分布的假设变得不切实际，导致ON/OFF模型生成流量的合成流量的自相关函数并不满足实际网络流量的长相关特性。虽然研究人员在ON周期持续时间的概率分布上做了一些改变（将轻尾分布变成重尾分布），但是实验结果仍然不尽如人意，存在着合成流量Hurst参数偏小的问题，即合成流量的长相关特性与实际网络流量的长相关特性相比不够显著。针对这一问题，有必要对ON/OFF模型之间不独立的情况进行研究，考察合成流量的性质与ON/OFF模型各源之间相关性的关系，根据研究结果，对ON/OFF模型加以改进，使之成为符合网络流量长相关特性的新模型。后文将以网络趋同性现象为基础，从理论和仿真实验两方面论证新模型生成流量的长相关性质。

3 引入趋同性的ON/OFF模型流量性质

3.1 理论分析

首先给出ON/OFF模型的结构图及其周期示意图，分别如图(1)、图(2)所示。每个ON/OFF源在各自的ON周期内随机发送数据包，在OFF周期内停止发送（ON周期和OFF周期的持续时间服从某种随机分布），以此来模拟数据网络中各终端用户产生的流量，最终汇聚成输出总流量，代表骨干网链路上的流量。

假设ON/OFF模型中有N个ON/OFF源，每个ON/ OFF源产生的流量分别是X1(m)、X2(m)、……、XN(m)，其中m为整数离散时间，m≥0。这N个源生成流量的合成流量X(m)为：

设n为时间间隔，n为大于等于零的整数，那么，X(m)的自相关函数为：

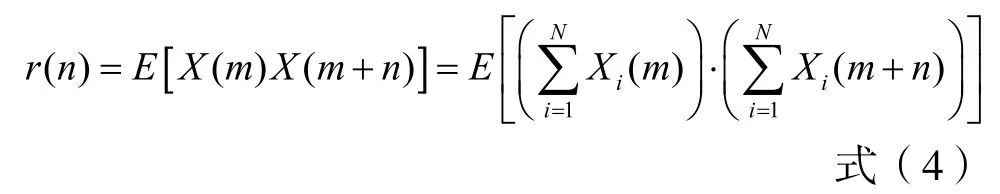
将上式展开，有：

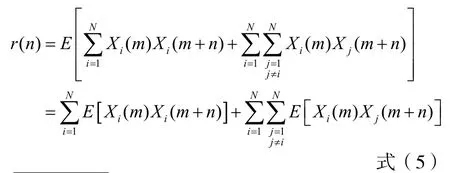
图1 ON/OFF模型Fig.1 ON/OFF model

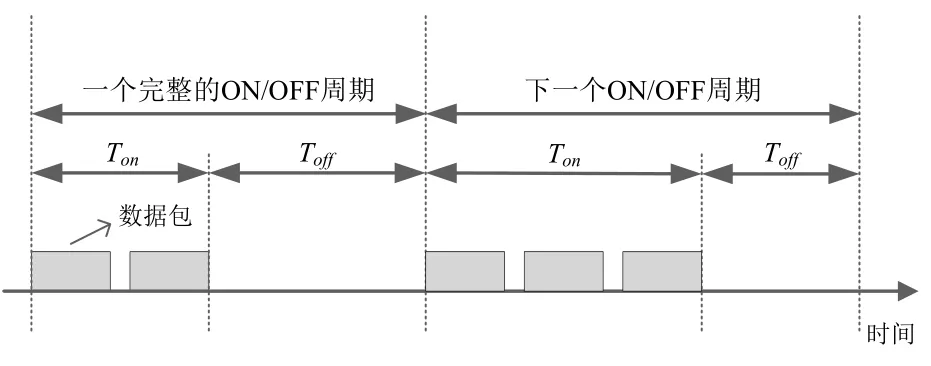
图2 ON/OFF模型的周期Fig.2 Period of ON/OFF model

当{Xi(m),m=0,1,2…}满足独立同分布条件时（i=1,2,3,…,N），令Mi=a，根据自协方差函数与自相关函数的关系：

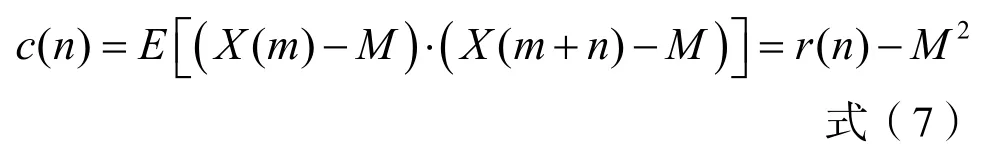
有下式成立：

把上式第二项中的 拆为，则有如下结果：

设每个Xi(m)的自协方差函数为ci(n)，则：

至此，本文得出了N个独立同分布ON/OFF源的合成流量的自协方差函数与每个源流量自协方差函数的关系。V.Paxson等人[15]指出，ON周期或OFF周期的持续时间具有轻尾分布的ON/OFF模型在独立同分布条件下产生的合成流量是短相关流量，所以，当每个ON/OFF源的ON、OFF周期的持续时间都被预先设置为轻尾分布时（如指数分布），合成流量的自协方差函数c(n)是可加的（在连续条件下即可积的），也就是说：

那么，当N为有限值时，必有：

上式说明，当ON/OFF结构模型满足独立同分布、ON周期或OFF周期持续时间呈轻尾分布时，单个源产生的流量具有短相关性质。

接下来考察另外一种情况，即：ON/OFF模型各个源的ON周期或OFF周期持续时间不独立。

仍然假设各个源的ON周期或OFF周期持续时间分布的期望均为a，根据式(4)、式(5)、式(6)，有：

式（13）的第一项与第二项恰好分别是各个源产生流量的自协方差函数与互协方差函数，即：

由于之前的假设中，各源之间不独立，具有一定的相关性，因此式(14)中的互协方差函数必然不为零。那么，在计算c(n)的可加性时，必须对各源产生的流量之间的互相关性加以考虑。与前一步的假设条件相比，仅仅更改了独立性这个条件，而ON周期或OFF周期的持续时间的概率分布函数依旧保持为指数分布，也就是说，单个源生成流量的自协方差函数仍然可加。这意味着，单个流量之间的互协方差是否可加将直接决定聚合流量自协方差函数是否可加，即各源生成流量之间的互相关性的强弱决定了合成流量自协方差的可加性。

另外，当ON/OFF模型各源ON周期或OFF周期持续时间呈重尾分布时，根据文献[17]的结论：如果各源生成流量之间独立同分布，那么合成流量将具有长相关性质。那么，令ON/OFF模型只有一个流量生成源，则合成流量（即此唯一的ON/OFF源生成的流量）也是长相关流量。这就是说，只要满足独立同重尾分布这个条件，无论单个流量还是合成流量都是长相关流量。如果各源之间不独立，具有一定相关性，那么，对于重尾分布来说，合成流量必然长相关。这是由于在式(14)中，第一项在重尾分布的条件下已经不可加，第二项只可能增强合成流量自协方差函数的不可加性，所以c(n)必然不可加。

3.2 流量性质的验证

为了验证以上结论，本节将仿真实验分为四组进行对比。实验中采用归一化自协方差函数和Hurst参数做为衡量实验结果的评价标准，根据归一化自协方差函数的衰减速度和Hurst参数估计值来判断合成流量是否长相关。归一化自协方差函数定义如下：设k表示时间间隔变量，c(k)为某随机过程的自协方差函数，随机过程的方差是2σ，那么，这个随机变量的归一化自协方差函数R(k)是：

归一化自协方差R(k)又称为自相关系数。

Hurst参数的估计方法有很多，本文采用方差时间法和R/S图法来估计仿真实验中合成流量的Hurst参数。

第一组实验的条件设置如下：ON/OFF模型各源的ON、OFF状态周期均呈轻尾分布（为了让实验具有可比性，一致选取指数分布作为轻尾分布的代表），且各源之间相互独立。从图3可以发现，互相独立呈轻尾分布的ON/OFF模型生成流量的合成流量的归一化自协方差函数衰减很快，在时间间隔之后，便在纵轴零点附近震荡，根据短相关过程自相关函数快速收敛为零的特点，容易判断第一组实验数据是短相关数据。

图3 合成流量归一化自协方差函数对比Fig.3 Contrast of normalized autocovariance functions of aggregation traffic

第二组实验的条件设置如下：ON/OFF模型各源的ON、OFF状态周期均呈轻尾分布（指数分布），但各源之间不独立，具有一定相关性。从图3可以发现，与第一组实验结果相比，第二组实验的归一化自协方差函数衰减十分缓慢，直到时间间隔 仍然没有衰减为零，而且在时间间隔 时出现了一个“尖峰”，说明在这样的设置条件下，数据的归一化自协方差函数存在一定的起伏，这是ON/ OFF模型各源之间的相关性较大所导致。

第三组实验的条件设置如下：ON/OFF模型各源的ON、OFF状态周期均呈重尾分布（选取Pareto分布作为重尾分布的代表），且各源之间相互独立。实验结果符合文献[13]的研究结果，第三组实验数据具有长相关性。与第二组实验结果比较之后发现，两组的归一化自协方差函数衰减速度相近，所以第二组实验数据也具有长相关性。

第四组实验的条件设置如下：ON/OFF模型各源的ON、OFF状态周期均呈重尾分布（Pareto分布），各源之间不独立，具有一定相关性。从图3可以看出，第四组的衰减速度比第三组要缓慢得多，这说明ON/OFF模型各源之间的相关性增加了长相关性的程度，使得归一化自协方差函数的衰减更慢，合成流量的长相关性更显著。

这四组实验数据的Hurst参数值分别采用方差时间法和R/S图法两种方法估计，估计结果见表1。如表1所示，各组实验的Hurst参数值表征了各组数据的长相关性，其中：各源之间独立同轻尾分布的ON/OFF模型合成流量Hurst参数值小于0.5，是短相关的；其余三种类型的ON/OFF模型合成流量Hurst参数值均大于0.5，因此都是长相关流量。从表1还可以发现，各源之间不独立的轻尾分布ON/OFF模型合成流量与各源之间独立同重尾分布的ON/OFF模型合成流量的Hurst参数值相差不大，自相似程度相近；而各源之间不独立、重尾分布的ON/OFF模型合成流量的Hurst参数值较大，更接近于1。这说明，在各源之间增加相关性，即使ON/OFF模型的ON周期和OFF周期持续时间呈轻尾分布，也可使合成流量具有自相似性；假如ON周期和OFF周期持续时间呈重尾分布，那么各源之间的相关性将加剧合成流量的自相似程度，增大Hurst参数值。

通过自相关函数衰减速度的对比和Hurst参数的估计，两种方法得到的结论基本一致。将本节得出的结论整理于表2，“单个源”是指只有一个ON/ OFF源产生流量数据，“多个源独立”是指存在多个独立同分布的ON/OFF源，“多个源相关”是指存在多个互相相关的ON/OFF源。

表1 不同类型ON/OFF模型的Hurst参数估计结果Tab.1 Estimated results of Hurst values with ON/OFF models

表2 不同条件下流量相关性的结果Tab.2 Results of traffic correlation on different conditions

4 C-ON/OFF模型的实验结果与分析

根据前一节的讨论可知，当ON/OFF模型各源之间存在相关性时，可以增加合成流量的长相关特性，特别是当ON/OFF模型各源的ON周期持续时间概率分布为重尾分布时，合成流量的长相关特性进一步增强。对于ON/OFF模型这种建立在网络流量汇聚过程模仿的物理模型来说，明确的物理意义和符合实际网络模式的特性就变得尤为重要，这是物理模型建模的根本。所以，要对现有的ON/OFF模型进行改进，根据第2节所提到的趋同性，考虑各ON/OFF源之间的趋同因素，把各源间的互相关性加入到新的模型当中，使之成为切合实际、符合需要的网络流量模型。

根据用户的网络行为趋同性，可以合理的假设各终端产生的流量波形大致相同、仅存在一定延时。根据这个假设条件，结合图1中ON/OFF模型的结构，可将某一ON/OFF源的生成流量分别延迟0、n、2n、3n、……、Nn个时间单位（n、N均为大于等于1的整数），每次延迟后的流量相当于一个终端生成的流量，将原始流量与延迟流量叠加，得到最终的汇聚流量。这些延迟流量相当于图1中其他ON/OFF源的生成流量，由于原始流量与延迟流量之间存在的差异仅是时间上的延迟，所以彼此之间具有一定的相关性，这就改变了经典ON/OFF模型中各源独立的特征，可基于“不独立”的新特征对经典ON/OFF模型进行改进。在此，将改进后的ON/ OFF模型命名为C-ON/OFF。

图4是C-ON/OFF模型的结构图，在一个ON/ OFF源后加入N个延迟单元，其中每个延迟单元的延迟时间相同，均为n个时间单位，将得到的 个流量叠加，获得最终的生成流量。在这里，N可以视为用户数量，即经典ON/OFF模型中ON/OFF源的个数，n可以看作用户网络行为在趋于一致过程中的反应时间，N和n都是具有实际意义的参数。

对C-ON/OFF模型生成流量性质的验证，本文采用流量数据的归一化自协方差作为评价指标，这是由于：网络流量模型的优劣在于模型是否能够刻画网络流量长相关特性，而非捕捉流量数据的幅度、均值、方差等统计性质，因此，网络流量长相关性质所特有的归一化自协方差函数慢衰减现象是否明显将决定网络流量模型的有效性和实用性。

为研究参数N和n对模型生成流量性质的影响，分别进行如下两组实验：

（1）固定n，观察C-ON/OFF模型生成流量的归一化自协方差随N值的变化情况；

（2）固定N，观察C-ON/OFF模型生成流量的归一化自协方差随n值的变化情况。

将两组实验的实验结果与延迟单元之前的单个ON/OFF源的生成流量进行比较，观察流量汇聚前后的差异。实验（1）和实验（2）中，延迟单元之前的单个ON/OFF源的ON周期和OFF周期的概率分布均设置为轻尾分布（本文中选取的轻尾分布为指数分布）。

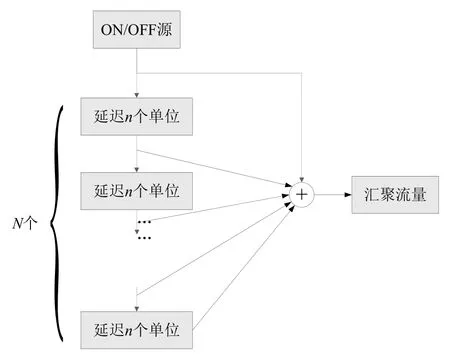
图4 C-ON/OFF模型结构Fig.4 Structure of C-ON/OFF model

图5 C-ON/OFF模型生成流量的归一化自协方差随N值变化关系Fig.5 Variation of C-ON/OFF model generating traffic's normalized autocovariance related to parameter N

图5和图6分别为实验（1）和实验（2）的仿真结果，其中，参数值为“n=0，N=1”时的曲线代表延迟单元之前的单个ON/OFF源生成流量的归一化自协方差。与上一节的研究结果相同：由于事先将ON/OFF源的ON周期和OFF周期的概率分布设置为指数分布，所以该曲线表现出短相关性质，衰减速度很快，当横轴的时间间隔大于1之后，曲线几乎始终在纵轴零点附近游荡。这两幅图中的其余曲线，代表不同参数设置下的C-ON/OFF模型生成流量的归一化自协方差，可以明显看出，这些曲线的衰减速度很慢，在横轴的时间间隔大于2之后，几乎看不出明显的下降趋势，这与长相关流量的性质极为相似。

图5中，当n值固定时，归一化自协方差的衰减速度随N的增大而趋缓，并且当图中各曲线的参数N相差为5时，衰减速度的差异十分显著，但在N=30和N=25时，两条曲线差别较小，这说明归一化自协方差随N值的变化有上界，当N值达到并超过这个上界时，N值对归一化自协方差的影响几乎不存在。在C-ON/OFF模型的使用中，N值应在10和25之间的整数中选取。N可做为模型的粗调参数，用于选择所需生成流量的归一化自协方差的大致衰减速度。

图6中，当N值固定时，归一化自协方差的衰减速度随n的增大而逐渐趋缓，但在某些时间间隔上，又出现了n值较小但归一化自协方差较大的现象，这说明当N值固定时，生成流量的归一化自协方差随n值的变化不太明显，在C-ON/OFF模型中，适合做为精调参数，在N值选定的基础上，对生成流量的归一化自协方差衰减速度进行细微调整以求达到要求。

图6 C-ON/OFF模型生成流量的归一化自协方差随n值变化关系Fig.6 Variation of C-ON/OFF model generating traffic's normalized autocovariance related to parameter n

为进一步量化参数N和n与生成流量归一化自协方差的关系，计算了实验（1）与实验（2）中相应生成流量的Hurst参数值以及相应归一化自协方差的均值（除去归一化自协方差在零点的值），分别将计算结果列于表3和表4。归一化自协方差的均值可以表征其衰减速度，对于长相关流量的归一化自协方差函数来说，均值越大表明衰减速度越慢，而衰减速度越慢则说明生成流量的长相关性质越显著，相应生成流量的Hurst参数值证明了这一点。表3和表4的最后一行为单个ON/OFF源在指数分布条件下的生成流量性质，可以看出该流量的归一化自协方差的均值近似为零，说明其衰减速度极快，迅速衰减为零，该流量具有明显的短相关性，Hurst参数值0.1943（小于0.5）也表明其短相关性。

在表3和表4中，随着N值（或n值）的逐渐减小，Hurst参数值不断降低，但始终大于0.5，这说明生成流量均为长相关流量。此外，与Hurst参数值的下降趋势相同，归一化自协方差的均值也随着N值（或n值）的减小而降低。

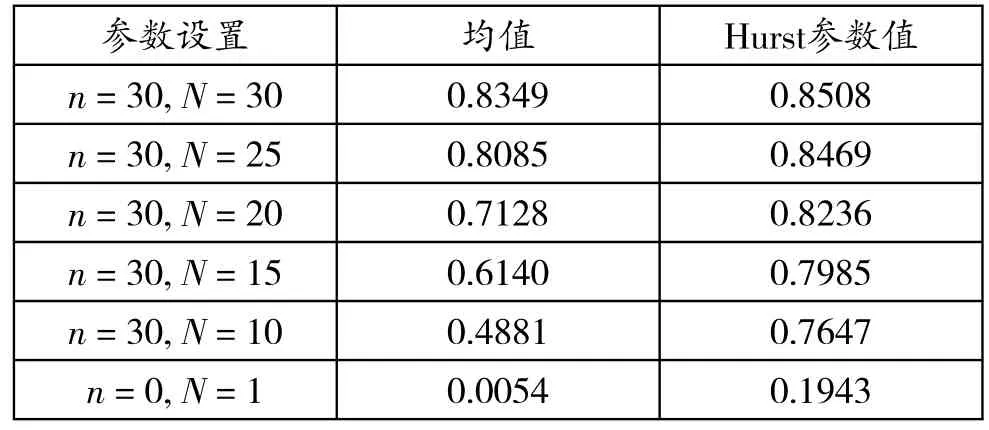
表3 不同参数条件下生成流量的统计结果及Hurst参数值（I）Tab.3 Statistic results and Hurst values of generating traffic's normalized autocovariance with different parameters (I)

如果把图4所示的C-ON/OFF模型中ON/OFF源的ON周期的概率分布设置为Pareto分布，那么，根据Pareto分布的方差无穷特点，ON/OFF源的ON周期持续时间的长度将具有极高的可变性，对于在ON周期以恒定速率生成数据包的ON/OFF源来说，其生成的数据包数量也将具有极高的可变性，在流量波形上则表现为流量数据的高突发性。因此，C-ON/ OFF模型生成具有极高突发性的流量，需要设置的参数如表5所示，其中符号“√”表示需要设置，符号“×”表示模型中不存在该参数、无需设置。

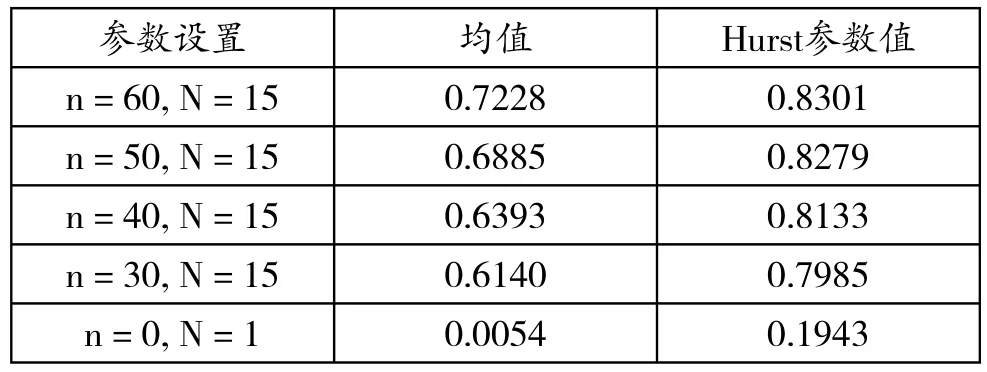
表4 不同参数条件下生成流量归一化自协方差的统计结果及Hurst参数值（II）Tab.4 Statistic results and Hurst values of generating traffic's normalized autocovariance with different parameters (II)

表6列举了几种常见的网络流量模型，从流量是否长相关、模型是否具有物理意义以及模型复杂度等方面与C-ON/OFF模型进行了对比。从表6可以看出，在建立具有长相关特性的网络流量模型时，C-ON/OFF模型在以上三个方面均占有优势。

表5 C-ONOFF模型的参数Tab.5 Parameters of C-ON/OFF model

表6 几种常见模型的对比Tab.6 Comparison of some familiar models

5 结束语

本文提出了Internet网络中用户网络行为的趋同性现象，并依此为依据对经典ON/OFF模型进行了改进。首先研究了经典ON/OFF模型与改进的ON/ OFF模型的生成流量的性质，通过理论分析证明了如下结论：在经典ON/OFF模型的基础上加入各ON/ OFF源之间的时间相关性，可以在ON周期和OFF周期持续时间分布为轻尾分布的条件下产生长相关性质的流量；然后对上述结论进行了仿真验证，仿真结果表明：在ON/OFF模型各源之间增加相关性之后，即使ON/OFF模型的ON周期和OFF周期持续时间呈轻尾分布，合成流量依然具有长相关性，若ON周期和OFF周期持续时间呈重尾分布，那么各源之间的相关性将加剧合成流量的自相似程度，表现为Hurst参数值的增加；依据以上研究结果，建立了一种改进的ON/OFF模型：C-ON/OFF模型，对该模型生成流量的归一化自协方差性质进行了定量分析之后，深入讨论了C-ON/OFF模型中两个具有物理意义的参数（N和n）与生成流量归一化自协方差之间的关系。在C-ON/OFF模型与其他常见网络流量模型比较之后发现，C-ON/OFF模型具有结构简单、计算复杂度低、物理意义明确等优点。

（References）

[1]Leland W E,Taqqu M S,Willinger W,et al.On self-similar nature of ethernet traffic (extended version)[J].IEEE/ACM Transactions on Net-working,1994,2(1):1-15.

[2]Norros I.On use of fractional Brownian motion in theory of connectionless networks[J].IEEE Journal of Selected Areas in Communications,1995,13(6):953-962.

[3]Willinger W,Taqqu M S,Sherman R,et al.Self-similarity through high-variability:statistical analysis of Ethernet LAN traffic at the source level[J].IEEE/ACM Transactions on Networking,1997,5(1):71-86.

[4]马晓艳.网络流量模型化与拥塞控制研究[D].北京:北京化工大学,2012.MA Xiaoyan.Studies on Modeling and Congestion Control of Network Traffic[D].Beijing:Beijing University of Chemmical Technology,2012.(in Chinese)

[5]吴启武.基于分形理论的物联网分层业务模型与性能分析[J].北京邮电大学学报,2012,35(4):38-41.WU Qiwu.Fractal-theory-based layered traffic model used in Internet of Things[J].Journal of Beijing University of Posts and Telecommunications,2012,35 (4):38-41.(in Chinese)

[6]Beran J,Sherman R,Taqqu M S,et al.Long-range dependence in variable-bit-rate video traffic[J].IEEE Transactions on Communications,1995,43 (234):1566-1579.

[7]苏占波.基于FARIMA模型的网络流量建模与预测[D].成都:电子科技大学,2010.SU Zhanbo.Network Traffic Modeling and Predicting Based on FARIMA[D].Chengdu:University of Electronic Science and Technology of China,2010.(in Chinese)

[8]Gowrishankar,Satyanarayana P S.Neural-network-based traffic prediction for wireless data networks[J].International Journal of Computational Intelligence Systems,2008,1(4):379-389.

[9]Park D C.Structure optimization of bilinear recurrent neural networks and its application to Ethernet Network traffic prediction[J].Information Sciences,2009,10(5):1-11.

[10]冯兴杰,潘文欣,卢楠.基于小波包的RBF神经网络网络流量混沌预测[J].计算机工程与设计,2012,33(5):1681-1686.FENG Xingjie,PAN Wenxin,LU Nan.Chaotic prediction of network traffic based on wavelet packet[J].Computer Engineering and Design,2012,33(5):1681-1686.(in Chinese)

[11]Alarcon-Aquino V,Barria J A.Multi-resolution FIR neural-network-based learning algorithm applied to network traffic prediction[J].Applications and Reviews,2006,36(2):208-220.

[12]Markus L.,Philipp S.,Markus R..Parsimonious fitting of long-range dependent network traffic using ARMA models[J].IEEE Communications Letters,2013,17(12):2368-2371

[13]Dutta P,Guerraoui R,Pochon B.Time-complexity of local decision in distributed agreement[J].SIAM Journal on Computing,2007,37(3):722-756.

[14]Wei R,Beard R W.Consensus seeking in multi-agent systems under dynamically changing interaction topologies[J].IEEE Transactions on Auto-matic Control,2005,50(5):655-661.

[15]Paxson V,Floyd S.Wide area traffic:failure of poison modeling[J].IEEE/ACM Transactions on Networking,1995,3(3):226-244.

[16]张宾,杨家海,吴建平.Internet流量模型分析与评述[J].软件学报,2011,22(1):115-131.ZHANG Bin,YANG Jiahai,WU Jianping.Survey and analysis on Internet traffic model[J].Journal of Software,2011,22(1):115-131.(in Chinese)

Network traffic modeling based on homogeneity and ON/OFF

GAO Bo1,WANG Changwei1,DUAN Hu2
(1.Institute of Information Technology,Shenzhen Institute of Information Technology,Shenzhen 518172,P.R.China;2.School of Computer Shenzhen Institute of Information Technology,Shenzhen 518172,P.R.China)

A modified network traffic model named C-ON/OFF is established after research of ON/OFF model's characteristics and Internet users’ behavior homogeneity.By analyzing and simulating,the correlation between C-ON/OFF model's two meaningful parameters (N and n) and its traffic normalized autocovariance function is identified.Compared to other models,C-ON/OFF has such advantages as simple structure,low computational complexity and clear physical meaning.

homogeneity;long range dependence (LRD);network traffic modeling

TP393.06

：A

1672-6332（2014）01-0001-09

【责任编辑：杨立衡】

2014-1-10

广东省自然科学基金资助项目（S2013010012669）；深圳市科技计划资助项目（JC201105190829A，JC201006020811A，JCYJ20130401095947233）

高波（1982-），男（汉），黑龙江哈尔滨人，讲师，博士，主要研究方向：网络流量建模与预测、图像及视频处理；E-mail：gaob@sziit.edu.cn