基于粒子群算法的太阳能电动汽车复合能源系统优化

周世琼，郭桂芳，袁骥轩

（1.深圳信息职业技术学院交通与环境学院，广东 深圳 518172；2.西藏民族学院信息工程系，陕西 咸阳 711200）

基于粒子群算法的太阳能电动汽车复合能源系统优化

周世琼1，郭桂芳2，袁骥轩1

（1.深圳信息职业技术学院交通与环境学院，广东 深圳 518172；2.西藏民族学院信息工程系，陕西 咸阳 711200）

太阳能电动汽车的复合能源系统优化匹配问题可以看成一个多目标优化问题，两个相互冲突的目标是极大化系统的峰值功率满足率和极小化系统的成本，前者关系到系统的可靠性后者涉及到样车能否量产，所以两个优化目标都很重要。本文提出了改进的粒子群算法优化配置太阳能电动汽车复合能源系统，这种改进的粒子群算法引进了遗传算法里的变异算子，并且打破常规算法里的加速因子为常数的惯例而使加速因子随时间改变。优化结果显示：改进的粒子群算法也能够很好地解决复合能源系统的多目标优化问题。

太阳能电动汽车；粒子群算法；多目标优化

1 引言

能源危机向人类敲响了警钟，常规能源己面临枯竭。同时以化石能源为主体的能源结构对人类环境的破坏显而易见，每年排放的二氧化碳达210万吨，并呈上升趋势，冰雪消融，冰川退缩，全球气候变暖，空气中大量二氧化碳，粉尘含量己严重影响人们的身体健康，人类赖以生存的自然环境己遭到极大的破坏。太阳能电动汽车（Solar Energy Electric Vehicle简称SEEV）是一种节约石油资源、无污染的理想“零排放”汽车，并可加大非石油资源的利用率，无疑是解决上述问题的有效途径，因此受到了广泛的关注和重视。

目前，在太阳能电动汽车的复合能源系统中，国内外学者关于蓄电池容量和超级容量的确定分别进行了大量的研究。Egiziano 提出了一种使用光伏发电系统的混合太阳能汽车的非线性模型并讨论其实验特性[1]，Hammad 研究了和车厢相关的所有参数，为太阳能汽车的能源系统设计奠定了坚实的基础，Craparo 在TRNSYS(Transient Systems)框架的基础上构建了太阳能电动汽车仿真模型的代码，它是一个模块化的太阳能系统应用仿真程序[2]，而来自伦敦南岸大学的团队设计了一系列"Mad Dog" 太阳能电动汽车并在世界的太阳能车竞赛中取得成功等等。这些文献的研究主要集中在太阳能车或太阳能电动汽车的设计，建模和太阳能发电系统的应用上面，而对太阳能电动汽车的成本和可靠性考虑甚少。

本文把太阳能电动汽车的复合能源系统看成一个独立的小型光伏发电系统。以复合能源系统的辅助能源，即光伏电池组件和超级电容的一次性投资成本和峰值功率不满足率为优化目标（这里峰值功率的不满足率定义为一个循环工况内超级电容的能量不满足峰值功率需求的秒数），使用智能计算的方法来优化匹配太阳能电动汽车复合能源系统。首先，陈述问题；其次，给出复合能源系统各单元的数学模型；最后，使用改进的粒子群算法优化配置太阳能电动汽车复合能源系统。

2 数学模型

太阳能电动汽车复合能源系统主要由光伏电池、最大功率跟踪器、超级电容、铅酸蓄电池组、电机驱动控制器和电动机组成，其结构简图如图1所示。

图1 太阳能电动汽车发电系统结构图Fig.1 Solar power generation system in car

光伏电池用于将光能转换为电能，提供能量的来源。因为光伏电池输出V-I特性的非线性，其输出的功率随机性较大，在光伏电池和电动机之间接上超级电容就可以把这种随机能量储存起来供电动机需要的时候使用。电机驱动器用于驱动电机以及控制电机转速转矩等，同时也起到对储能电池放电进行控制的作用。电机把电能转换成机械能驱动车辆行驶。由此可见，太阳能电动汽车复合能源系统就相当于一个负载为电动机的带有储能系统的小型独立光伏发电系统。

3 储能系统的优化模型

3.1 优化模型

对于太阳能电动汽车复合能源的优化配置问题，可以通过一个抽象的模型来描述。在这个模型里，不考虑能量在传输路径里损失的能量。这里我们定义：在t时刻，从蓄电池输入或输出的能量为，从光伏电池输出的能量为，输入或输出超级电容的能量为，如图2所示。这里不考虑车辆的再生制动功能。

图2 能量流示意图Fig.2 Energy flow

对于太阳能电动汽车复合能量系统的优化匹配，车辆行驶中的需求功率对于给定的工况来说是既定的，它被认为是一个已知函数，可以用表示。

在车辆正常行驶的过程中，车辆的动力系统符合功率守恒的原则，即车辆行驶所消耗的功率等于蓄电池和超级电容所提供的功率和，功率守恒等式如式（1）：

因为在每一个能量传输的环节均有损失，所以在每个时间段内，我们需要考虑的不仅是通过能量传输环节传递到电动机的功率，而且还要考虑超级电容和蓄电池提供的总功率。在图2中，仅有一部分的超级电容和蓄电池的能量到达能量汇总结点。在优化模型中，我们可以定义取值均在0～1之间的三个效率函数来分别表示光伏电池、超级电容和蓄电池的效率。实际上，效率取决于功率，具体数值由实验的方法得到，为了突出问题的重点，在本文中我们对这三个值均取常量。T为车辆行驶的总时间。因此，在时刻t，蓄电池提供给电动机的总功率、超级电容提供给电动机的总功率和光伏电池提供给超级电容的总功率计算如下：

由于在式（2）～（4）中的分母小于1，所以车辆行驶过程中所消耗的总功率大于传输到电动机的功率积分量。

为了说明超级电容的充入或提供的能量，我们定义如下函数：

3.2 优化目标

假设太阳光辐射强度为实验地的平均水平。峰值功率不满足率（Loss of Peak Power Probability，简称LPPP）可以定义为：

对于太阳能电动汽车复合能源系统的优化匹配问题，目前鲜有使用多目标优化方法来分析求解的。为了“尽可能多地”利用可再生能源——太阳能，这里需要在复合能源的成本和峰值功率满足率之间选择一个平衡点。因此峰值功率的满足率可以选作系统设计的目标。这样，降低峰值功率不满足率和成本是复合能源系统优化设计的两个目标，显然这两个目标是相互冲突的。因此，得出一个多目标优化问题：

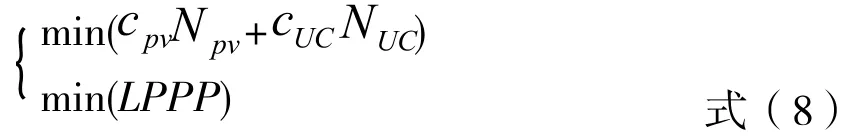
3.3 约束函数和决策变量

在时刻t，优化问题的约束函数为：

第一个等式反映了系统合理性的要求，在实验地平均辐射强度的水平下，光伏电池能够给超级电容充满。

第二个不等式是对系统可靠性的要求，即在车辆行驶的总时间内，超级电容和蓄电池储存的能量能够保证车辆正常行驶的要求。

第三、四个不等式分别是为了防止过充和过放对蓄电池组和超级电容器造成严重损害，直接影响蓄电池的使用寿命，所以对蓄电池组和超级电容器充放电容量的上下限进行限制。

4 基于改进粒子群算法的多目标优化

4.1 粒子群算法

粒子群算法（particle swarm optimization，PSO）模拟鸟集群飞行觅食的行为，鸟之间通过集体的协作使群体达到最优目的，是一种基于Swarm Intelligence的优化方法。在 PSO中，每个优化问题的解都被看成是搜索空间中的一只鸟。称之为“粒子(Particle)”。所有的粒子都有一个速度决定他们飞翔的方向和距离，每个粒子还有一个由被优化的函数决定的适应值。然后粒子们就追随当前的最优粒子的位置在解空间中搜索。

PSO算法数学表示如下：假设搜索空间为D维，总粒子数为n，第i个粒子位置的向量表达式为Xi=（xi1,xi2,…,xiD）；第i个粒子 “飞行”历史中的过去最优位置（即该位置对应解最优）向量为Pi=（pi1,pi2,…,piD），其中第g个粒子的过去最优位置Pg为所有Pi(i=1,…,n)中的最佳位置；第i个粒子的位置变化率即速度的向量为Vi=(vi1,vi2,…,viD)。则每个粒子的速度和位置更新方程为：

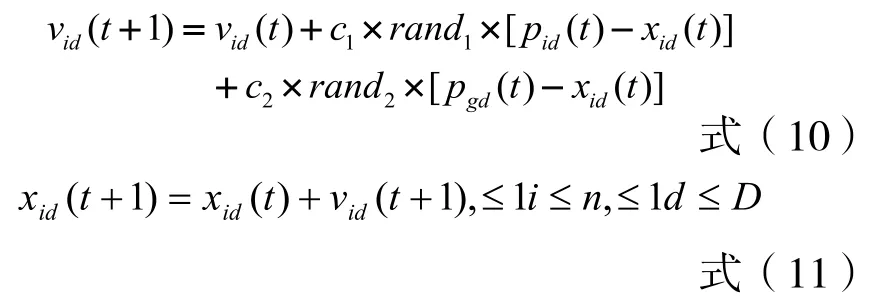
其中，c1，c2为正常数，称为加速系数或学习因子，分别调节向全局最优粒子和个体最优粒子方向飞行的最大步长，若太小，则粒子可能远离目标区域，若太大则会导致粒子突然向目标区域飞去或飞过目标区域[3,4]；rand1和rand2为[0，1]之间的随机数；第d（1≤d≤D）维的位置变化范围为[-xmaxd，xmaxd]，速度变化范围为[-vmaxd,vmaxd]，迭代中若位置和速度超过边界范围则取边界值。

4.2 改进粒子群算法的多目标优化

4.2.1 多目标粒子群优化算法

为了尽可能获得或接近Pareto最优解，映射到目标函数空间，要求算法在Pareto前沿面中保持种群的多样性，也就是要求粒子在Pareto前沿面上的尽可能均匀分布。

本文在适应度分配概念的基础上，把初始化后的种群划分为两个子群，一个称为支配子集（NP_set），另一个为非支配子集（P_set）。如果初始种群规模为N，P_set和NP_set的规模分别为N1和N2，一定有N1+N2＝N。

显然满足：

每次迭代只对NP_set中的粒子进行速度和位置的更新，在适应度分配概念的基础上，把更新后的NP_set中的粒子与P_set中的粒子进行比较。

粒子之间动态交换的策略：

4.2.2 改进的粒子群算法

这里提出的改进的粒子群（Improved Particle Swarm Optimization，简称IPSO）算法的策略就是使粒子群算法中的加速因子不是取固定值而是随时间变化的。改进粒子群算法流程如下：

第二步：随机初始化每个粒子的位置和速度，检查约束条件，条件满足继续下一步，否则再进行下一步；

第三步：利用目标函数分别计算粒子的适应度值，

在适应度分配思想的基础上，把初始化后的种群划分为两个子群，一个称为支配子集（NP_set），另一个为非支配子集（P_set），规模分别为N2和N1。

第四步：分别按式（10）和式（11）来更新NP_set内的每个粒子的速度和位置，如果速度/位置超过其各自的边界限制，则按边界取值，其中整个种群的Pgd从P_set子集中随机产生；

第六步：计算出的变异率pm对NP_set子群内所有粒子的各维变量的速度进行更新，更新粒子的新位置，检验约束条件；

交换xi、xj的位置，并更新各自集合中的位置和序号；

xi和xj中每一个xj比较以后，如果不存在j，使优于成立，显然也有可能是一个非支配解集，因此把纳入非支配解集。

更新P_set和NP_set子集，如果P_set或NP_set有重复的k个元素，删除重复的，并在NP_set中重新随机生成k个粒子。

更新N1和N2，直到N1＝N或达到最大迭代次数，否则跳转到第四步。

第八步：结束。

为了方便我们这里把具有随时间变化的加速系数的变异粒子群算法称为改进的粒子群算法(Improved Particle Swarm Optimization,简称IPSO)。通过式（12）的函数对比IPSO和基本PSO的性能。当时，通过求式（5-14）所示函数的最大值实现改进后的微粒群算法和基本微粒群算法的比较：

这里初始化参数：粒子群的数量为10；变量维数为2；最大迭代次数为200；最大和最小权重系数分别为0.9和0.4；加速因子和；粒子群的变异率最大和最小值分别取0.5和0；m取20。图3所示是改进的PSO和PSO算法的一次运行结果的对比。表1为分别经过20次运行后两种PSO算法所得结果平均值的对比。

图3 IPSO和PSO算法的一次运行结果的对比Fig.3 Comparison of a running result between IPSO and PSO

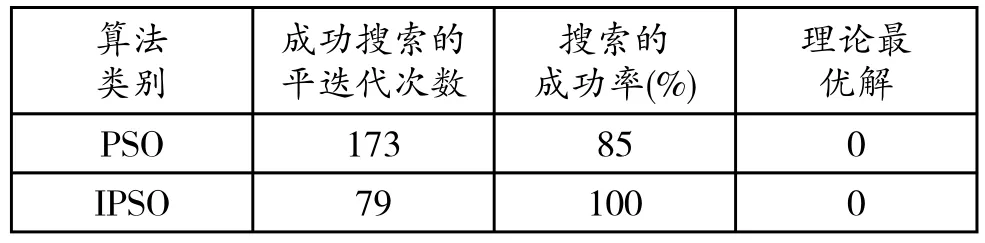
表1 分别运行20次后IPSO和PSO算法结果对比Tab.1 Comparison of 20 times running results between IPSO and PSO

从图3和表1可以看出，相对于PSO算法，改进后的PSO即IPSO收敛较快。

综上所述，改进的粒子群算法IPSO，无论是在全局寻优还是收敛速度等性能方面比起基本的粒子群算法PSO要改进很多。

5 基于粒子群算法的复合能源系统的多目标优化

图4 1月某天广州的太阳能辐射强度（从上午11：00：05到下午15：30：05点）Fig.4 Solar radiation intensity,taking a January day in Guangzhou 11:00:05 to 15:30:05

本章所使用环境数据如太阳辐射强度和环境温度是广州某校园内一月的实测数据，辐射强度S如图4所示，环境温度T为21℃左右。这里带有光伏电池最大功率跟踪器的光伏电池、超级电容和蓄电池功率的实际使用效率取值分别是：，，，且初始状态超级电容和蓄电池均满荷。

运用上文描述的光伏电池组件工程数学模型来计算各种外界条件下的光伏电池输出特性，太阳能电动汽车上单块光伏电池晶片的输出功率如图6所示。

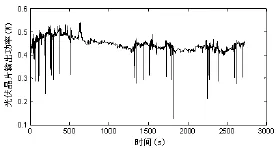
图5 单个光伏晶片的输出功率Fig.5 Output power of a photovoltaic cell

从图4和图5可知，在中午11点钟到15：30这段时间(温度变化不大)，光伏阵列输出的功率是随辐照强度的变化而变化，由于这段时间光照强度比较大，所以光伏阵列输出功率也比较大，大约在0.47W左右。

初始化运行的参数：种群数N=30，N1=15，N2=15变量维数D=2，最多迭代次数，最大和最小权重系数分别为wmax＝0.9和wmin＝0.4；加速因子；粒子群的变异率最大和最小值分别取。

图6 中国某实测工况所需求的功率Fig.6 Power demand of a real condition in China

使用图6所示的中国某道路的工况所需求的功率作为仿真依据，求解本章提出的多目标优化问题，种群的演化从图7多注的“Initial”开始，“Pareto Front”为所求的非支配解集。从图中可以看出，虽然决策变量是在其取值范围内随机产生，并且和“Pareto Front”相差较远，非支配解前沿面在目标空间中具有广泛分布、非凸和不连续的性质，但是由于受到约束条件的限制其变化规律基本遵循非支配解的变化趋势。

图7 非支配解的前沿面Fig.7 Non-dominated frontier solutions

以Pareto解集中的一个解为例，对于给定的LPPP=0.07，这里 Cost＝10,578元。这时光伏电池单体串联数和超级电容单体的串联数分别是25和18。

从运行的结果来看，LPPP的范围是[0，0.07]时，复合能源系统的价格在10,578元和11,802元之间变化，光伏电池单体串联数范围为[25，46]，超级电容单体串联数范围为[17，20]。从图7优化的结果来看，在Pareto解集中，随LPPP的减小，光伏电池和超级电容的成本之和也是一直减小的，最后达到优化的目的。

计算机CPU为Intel Pentium Processor 2.83GHz，内存为3.00GB，软件平台为MATLAB7.1，运行时间为5分钟。

6 结论

本章在基本粒子群算法的基础上，提出了改进的粒子群优化算法。通过对多元函数的优化，对比基本的粒子群算法和改进的粒子群算法的特性，后者较前者能够较快地收敛到最优解。

太阳能电动汽车的复合能源系统优化匹配问题可以看成一个多目标优化问题，两个相互冲突的目标是极大化系统的峰值功率满足率和极小化系统的成本，前者关系到系统的可靠性后者涉及到样车能否量产，所以说两个优化目标都很重要。基于Pareto适应度分配策略得到Pareto非支配解，改进的粒子群算法也能够很好地解决复合能源系统的多目标优化问题。

References)

[1]Bull S R.Renewable energy today and tomorrow[J].Proceedings of the IEEE,2001,89(8):1216-1226.

[2]茆美琴、余世杰、苏建徽等.风/光复合发电系统变结构仿真建模研究[J].系统仿真学报,.2003,15 (3):361-364.MAO Meiqin,YU Shijie,SU Jianhui.Variable structure modeling of hybrid power system[J].Journal of System Simulation,2003,15 (3):361-364.(in Chinese)

[3]曾建湖，介婧，崔志华.微粒群算法[M].北京：科学出版社．2004.ZENG Jianhu，JIE Jing，CUI Zhihua.Particle Swarm Optimization[M]．Binjing：Science Press．2004．(in Chinese)

[4]王凌.智能优化算法及其应用[M]．北京：清华大学出版社，2001．WANG Ling.Intelligent Optimization Algorithms with Applications[M]．Beijing:Tsinghua University Press，2001.(in Chinese)

Optimization of hybrid power system based on particle swarm algorithm

ZHOU Shiqiong1,GUO Guifang2,YUAN Jixuan1

(1.School of Traffic and Environment,Shenzhen Institute of Information Technology ,Shenzhen 518172,P.R.China;2.Department of Information Engineering,Tibet University for Nationalities,Xianyang 711200,P.R.China )

The sizing of hybrid power system（HPS）can be taken as a multi-objective optimization problem involving two conflicting objectives as minimization of cost and minimization of loss of peak power probability (LPPP).The improved particle swarm optimization (IPSO) algorithm is proposed for the optimal sizing of HPS problem which combines the PSO with the mutation operator and updates the acceleration factors with time varying.Comparing with the optimization results using adaptive genetic algorithm (AGA),this proposed method is also well suitable for obtaining the solution of multi-objective optimization problem.

solar electric vehicle；particle swarm algorithm ；multi-objective optimization

TN3

：A

1672-6332（2014）01-0010-06

【责任编辑：杨立衡】

2013-11-12

The research is supported by a grant from National Natural Science Foundation of China（No.51166012）

周世琼(1976-)，女（汉），河南信阳人,副教授,博士，主要研究方向:新能源汽车能量管理；E-mail:zhoushiqiong@sohu.com