求解约束优化问题的偏好多目标进化算法

董 宁,王宇平

(1.西安电子科技大学数学与统计学院,陕西西安 710071; 2.西安电子科技大学计算机学院,陕西西安 710071)

求解约束优化问题的偏好多目标进化算法

董 宁1,王宇平2

(1.西安电子科技大学数学与统计学院,陕西西安 710071; 2.西安电子科技大学计算机学院,陕西西安 710071)

将约束优化问题转化为双目标优化问题,用进化算法求解转化的双目标问题.设计了新的混合交叉算子以提高算法在进化过程中的搜索能力,加快算法收敛;借鉴多目标优化加权度量法中成绩标量函数的特点,提出新的偏好适应度函数,进行个体比较和选择.新适应度以个体到参考点的加权距离衡量个体优劣,参考点和权向量体现选择的偏好.在进化过程中,自适应地选择参考点和权向量平衡进化的不同阶段对各个目标的偏好程度,增加种群多样性,避免算法早熟收敛.

约束优化;多目标优化;进化算法;偏好;成绩标量函数

约束优化问题是科学和工程应用领域经常出现的一类数学规划问题,也是优化领域一类很难处理的问题.进化算法是一种基于群体的搜索方法,它能有效地解决复杂问题,因此适合于求解约束优化问题,近年来引起许多学者的关注,并涌现出大量的约束优化进化算法[1-6].用进化算法求解约束优化问题,其性能好坏取决于两个因素:一是进化算法的搜索机制,二是约束处理技术[6].由于约束优化问题是要找到满足约束条件的最好解,约束满足是首要问题.如何用约束条件和目标函数定义适应度函数是至关重要的,也是非常困难的,因为此时适应度函数不仅要评价解的好坏,还要反映解与可行域的距离.约束优化进化算法发展初期,一些算法认为可行解总是优于不可行解[2,7],进化搜索过程中过分强调可行解的作用,忽略甚至抛弃不可行解携带的有用信息,而对于最优解位于可行域边界的优化问题,从约束违反小的不可行解出发比从远离边界的可行解出发更容易找到全局最优解.忽略或者抛弃这些不可行解,算法性能将大受影响.利用罚函数思想,将约束优化问题转换为多目标优化问题是近年来处理约束的一种有效方法[8-9].在求解转化的多目标问题时,如果用Pareto支配关系比较个体,即认为目标函数和约束满足同等重要,一些远离可行域但目标函数值较小的不可行解首先被保留下来,而实际上,这些解对某些问题(如最优解在可行域内部)的寻优没有帮助.因此在进化搜索过程中,个体的比较和选择是影响算法效率的重要因素,应设计恰当的适应度函数以平衡进化过程对约束满足和目标函数最优的偏好.

笔者将约束优化问题转化为双目标优化问题[8-9],设计了新的进化算法求解这个有偏好的双目标优化问题.在进化算法搜索时,设计了新的混合交叉算子,保证在进化初期群体快速向可行域靠近,在进化后期快速收敛到全局最优解.在约束处理技术上,将原问题转化为双目标问题,借鉴多目标优化中的加权度量函数——成绩标量函数(ASF)的特点,将原问题的目标函数和约束违反函数标量化为适应度函数,该函数使用参考点和加权向量平衡进化过程对不同目标的偏好程度.在进化过程中,根据群体特征,自适应地确定参考点和加权向量,使算法在进化初期偏好约束满足,在进化后期偏好原问题的目标函数,保证进化过程中群体的多样性和个体的最优性,使算法快速找到全局最优解.

1 约束优化问题及相关概念

1.1 约束优化问题

不失一般性,考虑如下的约束优化问题:

其中,x=(x1,x2,…,xn)∈S⊂Rn,是决策向量.一般地,搜索空间S={x∈Rn|li≤xi≤ui,i=1,2,…,n},其中,ui∈R,li∈R,分别表示xi的上下界;f(x)是目标函数;gi(x)≤0,是不等式约束;hj(x)=0,是等式约束;Ω={x|x∈S,gi(x)≤0,hj(x)=0,i=1,…,q,j=q+1,…,m},称为问题(1)的可行域,可行域中的点称为可行解.

1.2 问题的转化及相关概念

传统的罚函数法是求解约束优化问题时常用的约束处理方法,但罚参数的选取比较困难,且罚参数的取值直接影响算法的性能.此外,在基于罚函数的处理方法[7]中,当进行个体比较时,可行解总是优于不可行解;对全局最优解位于可行域边界附近的优化问题,从位于最优解附近的不可行解出发比从远离最优解的可行解出发更容易找到最优解.如果忽略这些不可行解,算法的效率将受到影响.利用罚函数思想将约束优化问题转化为有两个目标的多目标优化问题是近年来处理约束的有效方法[8-9],具体转化方法为:

其中,δ为等式约束条件的容忍值,一般取较小的正数.显然,Gi(x)≥0.若Gi(x)=0,则x满足第i个约束条件;若Gi(x)＞0,则Gi(x)表示x违反第i个约束条件的程度.定义约束违反函数,它表示个体x违反所有约束条件的程度,同时也反映了个体x离可行域的距离.

将问题(1)的目标函数f(x)作为一个目标,将约束违反函数G(x)作为另一个目标,则问题(1)可转化为有两个目标的多目标优化问题:

其中,x∈S⊂Rn,是决策向量;S称为决策空间,x∈S的像空间称为目标空间.为简单起见,将问题(3)的两个目标记为f1(x)=f(x),f2(x)=G(x).下面给出双目标优化问题的基本概念.

定义1(Pareto支配) 设向量u=(u1,u2),u Pareto支配(Pareto非劣于)向量v,v=(v1,v2),记为u≺v,当且仅当u1≤v1且u2＜v2,或u1＜v1且u2≤v2.

定义2(Pareto最优解) 向量xu∈S,称为双目标问题(3)的Pareto最优解(Pareto非劣解),当且仅当xv∈S,使得v≺u,其中,u=(f1(xu),f2(xu)),v=(f1(xv),f2(xv)).

定义3(Pareto最优解集) 对双目标优化问题(3),Pareto最优解集合记为PS,则

定义4(Pareto前沿) 对双目标优化问题(3),Pareto最优解集合PS在目标空间中的像称为Pareto前沿,记为PF,则

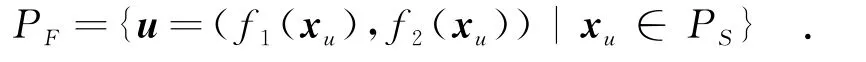
虽然将约束优化问题(1)转化成双目标优化问题(3),但是它们的解有着本质区别,如图1所示.问题(3)致力于找到位于Pareto前沿上均匀分布的代表解集,而问题(1)是要找到满足约束条件(即G(x)=0)且f(x)达到最小值的解,即Pareto前沿和可行域的交点f(x*).

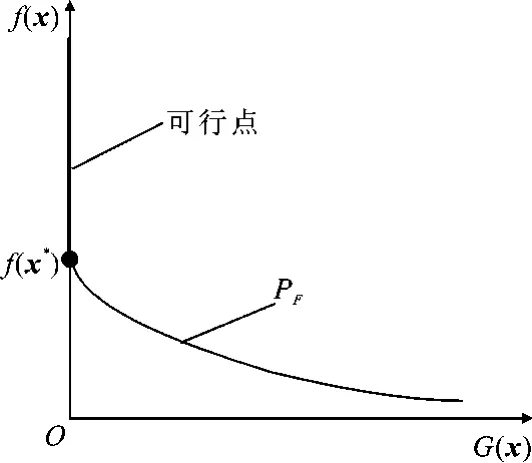
图1 双目标优化问题及约束优化问题最优解的关系

2 双目标进化算法

2.1 基于偏好的新适应度函数

在多目标进化算法中,个体间的比较是偏序关系,即当两个个体互相非支配时不能比较其优劣.利用双目标求解约束优化问题时,目的是找到满足约束(G(x)=0)且使目标函数f(x)达到最小的解,约束满足是首要问题,因此问题(3)实际上是有偏好的双目标问题.基于这一特点,借助多目标优化技术的加权度量法,将两个目标通过加权度量化为一个标量函数——成绩标量函数(Achievement Scalarizing Function,ASF),该函数通过加权向量和参考点体现对两个目标的不同偏好.对一般的双目标问题(极小化问题),成绩标量函数为

图2 多目标加权度量函数与成绩标量函数示意图

基于上述成绩标量函数的特点,结合约束优化问题最优解和多目标Pareto最优解的关系,将种群进化分为3个阶段.在每一阶段自适应选择参考点和权向量ω,以F(x)为适应度函数进行个体的比较和选择,实现在不同进化阶段偏好不同的目标.

第1阶段:群体中只有不可行解,即ρ=0(其中ρ表示群体中可行解的比例).此时个体的比较要偏好于约束满足,即约束违反小的个体.但是,如果只考虑约束,一些约束违反较小但目标函数值较大的个体会优先进入下一代,这些解对种群进化作用较小,而这种选择策略会忽略那些约束违反稍大,但目标函数较小的个体(即群体中一部分Pareto最优解).另外,还有一些算法采用多目标的Pareto排序法[11],这种方法认为所有目标同等重要,种群中所有Pareto最优解被赋予小的适应值,优先进入下一代.实际上,对于某些问题(如最优解在可行域内部),那些远离可行域且目标函数值较小的不可行Pareto解对寻优没有帮助.基于上述考虑,在这一阶段,在保证约束违反小的同时也要求目标函数值不太大.此外,由于群体中没有可行解,约束违反最小的非支配不可行解(称其为最好不可行解)是目前种群中的最好解,因此选择它作为参考点.由于此时群体进化方向偏好于约束满足,故取ω=(0.1,0.9),即离最好不可行解的ω加权距离式(4)越小,个体越好;反之越差.如图3(a)所示.

图3 进化不同阶段适应度函数的等高线及个体选择情况

第2阶段:群体中既有可行解也有不可行解,即0＜ρ＜1.若ρ较小,即可行解较少,要么进化处于初期阶段,要么可行域较小,找到可行解的难度较大,此时应偏好于可行解;若ρ较大,即可行解较多,则约束违反小的非支配不可行解比一些目标函数值较大的可行解更重要,特别是对最优解处于可行域边界或其附近的优化问题.在这一阶段,选择最好的可行解作为参考点.当ρ较小时,偏好于可行解(G(x)=0)及约束违反G(x)小的解;当ρ较大时,偏好于目标函数值f(x)小的个体.由于要求的是满足约束条件的最优解,约束满足是首要的,对目标函数的偏好不能太大,因此对目标函数的偏好权值设定上限为0.5,即,故如图3(b)和图3(c)所示.

第3阶段:群体中只有可行解,即ρ=1.由于只有可行解,因此按照目标函数值的大小比较优劣,即在式(4)中,最好的可行解作为参考点,权向量ω=(ρ,1-ρ)=(1,0).

以F(x)作为个体的适应度,适应度越小,个体越好.由于采用加权距离式(4)进行个体比较,为了避免目标函数f(x)与约束违反程度G(x)数量级不同对目标偏好的影响,先对目标函数f(x)和约束违反程度G(x)进行如下正规化:

其中,fmax和fmin、Gmax和Gmin分别表示f(x)、G(x)的最大值和最小值.由于已知Gmin=0,其他未知,因此用当前群体中f(x)的最大值和最小值、G(x)的最大值分别表示fmax,fmin和Gmax.此处不用当前群体中G(x)的最小值作为Gmin,是因为用该值正规化函数后,约束违反最小的不可行解将变成可行解.

2.2 混合交叉算子

用进化算法求解双目标优化问题式(3)时,进化初期群体中只有不可行解,而且这些不可行解的目标函数值通常较大.在这一阶段,需要设计有效的交叉算子使群体快速向可行域靠近,同时个体的目标函数值也得到改善,针对这一特点提出了非支配聚类交叉算子.随着种群进化,一些个体进入可行域,此时群体中既有可行解又有不可行解.针对很多约束优化问题的最优解位于可行域边界上或边界附近的特点,设计了可行解和不可行解之间的二分交叉算子,使群体向可行域边界聚集,加快收敛速度.

2.2.1 非支配聚类交叉算子

非支配聚类交叉算子用于不可行群体(即种群中只含有不可行个体).由于种群中只有不可行解,首先找到种群的所有非支配个体,每个非支配个体主导一个聚类.种群中的其他个体至少被一个非支配个体支配.根据支配关系将被支配个体聚入支配它的非支配个体主导的聚类,在每一个聚类内,让被支配个体向非支配个体靠近,从而使被支配个体沿不同方向向约束违反函数减小最快的方向移动,从而快速找到可行解.设第k代群体P(k)={x1,x2,…,xN},且G(xi)＞0(i=1,2,…,N).具体算法如下.

算法1 非支配聚类交叉.

(1)Pareto非支配解:找到P(k)的非支配个体.不妨设P(k)的前k个为非支配解,且其约束违反由小到大排列,记非支配解集合(k)={x1,x2,…,xk},令P(k)=P(k)(k),并将其元素表示为P(k)={y1,y2,…,yN-k}.

(3)交叉:每个聚类内只有一个非支配个体xi,其他个体yj都被xi支配,因此交叉分两种情形.

①对聚类内的支配个体yj,让yj沿着方向dj=xi-yj进行一维搜索,希望产生比xi和yj都好的后代yj+1=yj+αdj,其中,α＞0,为步长.因为xi≺yj,沿方向dj,个体yj的目标函数值f和约束违反函数G都可能下降.

②对聚类的主导个体xi,找约束违反比它小的主导个体进行线性交叉.

该交叉算子保证所有被支配解都向支配它且约束违反最小的非支配解靠近,既能保证约束违反减小,又使目标函数值得到改善,而且聚类方法保证在多个下降方向中,选择让约束违反函数减小最快的方向,使群体沿不同方向快速向可行域靠近,加快算法的收敛.

2.2.2 二分交叉算子

二分交叉算子用于既有可行解,又有不可行解的种群进化.设种群中要进行交叉的个体为xi.若xi是可行个体,则在种群中找到和它非支配的不可行个体xj进行配对,此时f(xj)＜f(xi).若xi为不可行个体,可分为如下两种情况:(1)若存在支配xi的可行个体xj,则将xj与xi配对,此时f(xj)＜f(xi)且G(xj)＜G(xi);(2)若不存在支配xi的可行个体,则任意找一个可行个体xj与xi配对,此时G(xj)＜G(xi),将配对的个体进行二分交叉生成后代xi+1=(xi+xj)/2,即取xi和xj连线的中点作为xi的后代,xi+1可看成将个体xi沿着由xi指向xj的方向向xj靠近.由于xj至少在一个目标上比xi好,从而上述配对进行二分交叉的方法使后代个体的目标函数值或者约束违反程度减小.此外,生成的个体可能是可行解,也可能是不可行解,维持了种群的多样性.

混合交叉算子对搜索空间进行线性搜索,加快了算法的收敛速度.为了避免算法早熟收敛,提高算法的搜索能力,在进化过程中引入单形交叉算子.

2.2.3 单形交叉算子

单形交叉算子[12]是进化算法中常用的交叉算子,它基于均匀分布产生后代个体,并且交叉过程不需要父代个体的适应值信息.单形交叉算子的搜索区域随着进化过程自适应地调整,保证了算子在进化初期具有较强的全局搜索能力,后期具有较强的局部搜索能力.具体步骤如下:

在Rn中,n+1个独立的父代个体xi(i=1,2,…,n+1)形成一个单形,首先以一定比例ε将单形沿各个方向xi-o(i=1,2,…,n+1)扩张形成一个新的单形,其中o是n+1个父代的中心,即,新单形的顶点yi=(1+ε)(xi-o),i=1,2,…,n+1.然后在新单形中任取一点作为后代个体z,即z=k1y1+ k2y2+…+kn+1yn+1+o,其中ki(i=1,2,…,n+1)是[0,1]上均匀分布的随机数,且k1+k2+…+kn+1=1.

2.3 双目标偏好约束优化进化算法

对转化的双目标优化问题(3),笔者提出的偏好进化算法步骤如下.

(1)初始化群体:随机产生规模为N的初始种群P(0)={x1,x2,…,xN},其中xi∈S(i=1,2,…,N),令k=0.

(2)交叉操作:计算种群中可行解的比例ρ.当0≤ρ＜1时,先对种群进行混合交叉,并采用稳态策略更新种群,对更新后的种群再进行单形交叉;当ρ=1时,对种群只进行单形交叉.将进行交叉的个体称为目标个体.

①混合交叉:以概率pc1选择交叉的个体.若ρ=0,对P(k)中个体进行2.2.1节的非支配聚类交叉.若目标个体是被支配个体,则后代个体直接代替目标个体;若目标个体是主导个体,且后代个体支配目标个体,或与目标个体互相非支配且后代个体的约束违反小,则后代个体代替目标个体,否则抛弃后代个体.若0＜ρ＜1,进行2.2.2节的二分交叉.若后代可行,则后代和可行父代中目标函数值小的代替可行父代;若后代不可行,则后代和不可行父代中约束违反值小的代替不可行父代.

(3)变异操作:设xi=(xi1,xi2,…,xin),是以概率pm从O1中选出进行变异的个体,对xi进行如下变异.(a)随机从xi=(xi1,xi2,…,xin)中选择一个基因位xik(k=1,2,…,n);(b)从[lk,uk]随机产生实数x′ik代替xik,得到变异后代x′i=(x′i1,x′i2,…,x′in),即

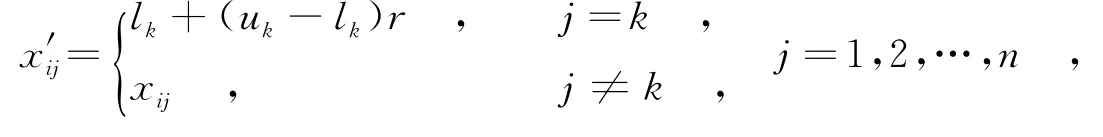
其中,r是[0,1]的随机数,变异后代集合记为O2.

(4)选择操作:在P(k)∪O1∪O2中,用2.1节的适应度函数选择适应值小的前N个个体作为下一代种群P(k+1).

(5)判断停止准则:若满足停止条件(通常采用目标函数值评估次数),则输出最优解;否则,令k=k+1,转步骤(2).

3 数值实验

3.1 测试函数及参数设置

为了测试笔者提出算法的有效性,采用文献[1]中6个常用的标准测试函数进行试验.实验中,参数取值如下:种群规模N=250,混合交叉概率pc1=0.5,单形交叉概率pc2=0.8,变异概率pm=0.1,单形交叉扩张比例ε=6,产生后代个数λ=5,适应度函数评价次数(FES)是240 000,等式约束违反的容忍值δ=0.000 1.对所有测试函数,独立运行30次,记录结果的最好值、平均值、最差值以及标准差.

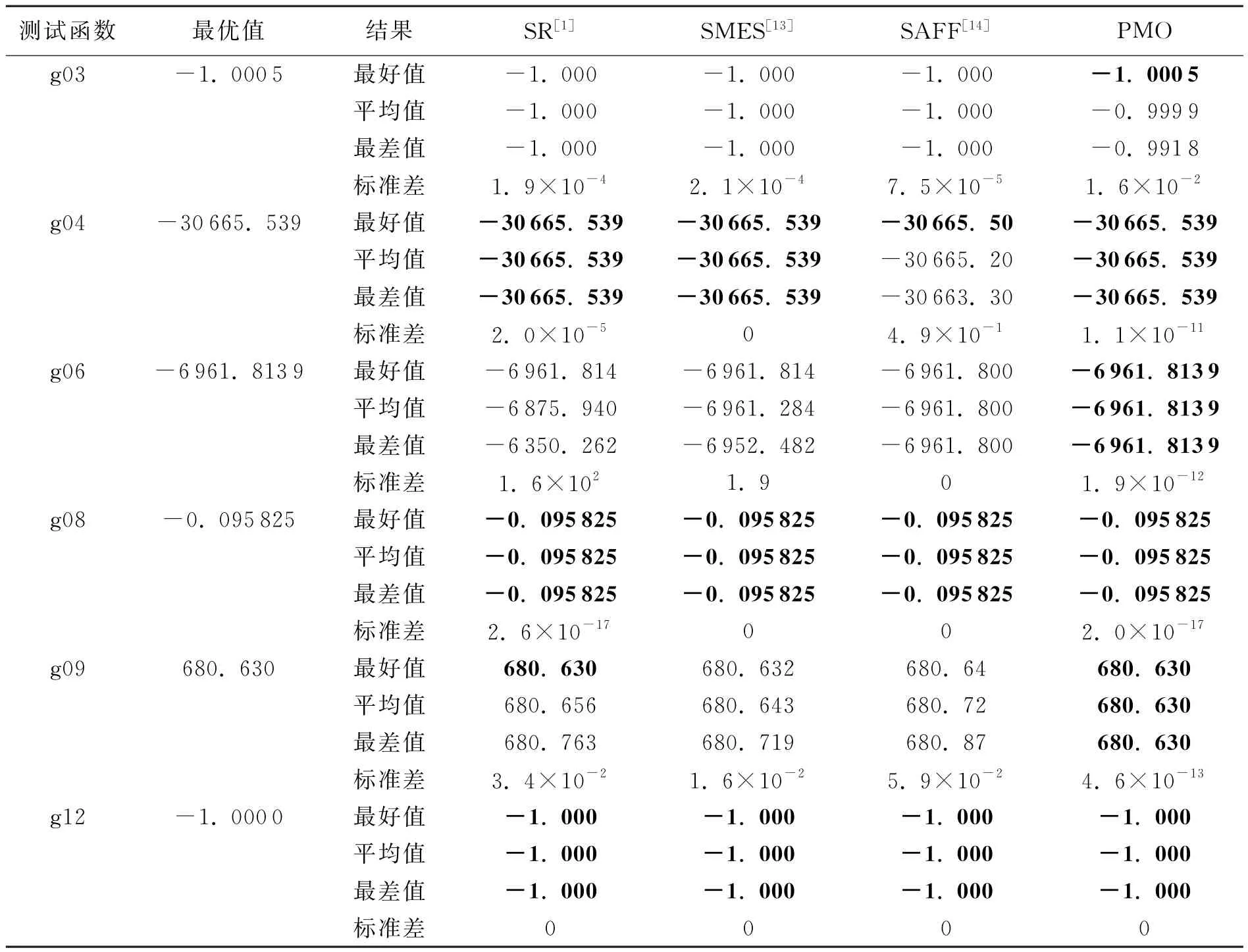
表1 笔者提出的算法(PMO)与经典算法SR,SMES和SAFF的实验结果比较

3.2 结果及分析

将笔者提出的算法(PMO)与另外3个经典高效的进化算法SR[1],SMES[13]和SAFF[14]进行比较.表1给出了各方法的最好值、平均值、最差值及标准差(3种经典算法的结果来自相关文献).从表1可看出,除g03外,笔者提出的算法在30次运行中都找到了全局最优解,且所得到解的最好值、平均值、最差值以及方差都比另外3种算法好,说明笔者提出的算法具有良好的稳定性.

此外,从函数评估次数来看,PMO为240 000次,与SMES算法相同,比SR算法的350 000次及SAFF算法1 400 000次都少.对于g03,笔者提出的算法找到了最优值,虽然在平均值、最差值上稍劣于其他方法,但是从30次运行的统计结果看,有18次得到的结果优于-1.000.如果将函数评估次数增加到350 000,进一步实验表明,30次独立运行结果中有15次找到全局最优解-1.000 5,此外还有12次的结果优于-1.000,只有3次的结果稍劣于-1.000.

以上结果表明,PMO算法用较少的计算次数得到的结果类似或优于另外3种算法,得到结果的方差更小,因此PMO算法具有较强的寻优能力和良好的稳定性.

4 总 结

笔者将约束优化问题转化为双目标优化问题,用进化算法求解转化后的问题.根据群体特征设计了混合交叉算子,保证群体在进化初期沿着不同方向快速向可行域靠近,加快了算法收敛.提出了新的带偏好适应度函数进行个体比较和选择,新适应度函数以个体到参考点的加权距离衡量个体优劣,参考点和加权向量体现了进化过程中选择的偏好.笔者将算法的进化过程分为3个阶段,在每个阶段,自适应地选择参考点和加权向量,实现进化过程对不同目标的偏好,使算法快速找到全局最优解.数值实验结果表明,笔者提出的算法对具有不同特点的测试问题是有效的,与3种经典算法[1,13-14]的结果对比,说明笔者提出的算法效率更高.

[1]Runarsson T P,Yao X.Stochastic Ranking for Constrained Evolutionary Optimization[J].IEEE Transactions on Evolutionary Computation,2000,4(3):284-294.

[2]Deb K.An Efficient Constraint Handling Method for Genetic Algorithms[J].Computer Methods in Applied Mechanics and Engineering,2000,186(2):311-338.

[3] 刘若辰,焦李成,雷七峰,等.一种新的差分进化约束优化算法[J].西安电子科技大学学报,2011,38(1):47-53. Liu Ruochen,Jiao Licheng,Lei Qifeng,et al.New Differential Evolution Constrained Optimization Algorithm[J]. Journal of Xidian University,2011,38(1):47-53.

[4]郑建国,王翔,刘荣辉.求解约束优化问题的ε-DE算法[J].软件学报,2012,23(9):2374-2387. Zheng Jianguo,Wang Xiang,Liu Ronghui.ε-Differential Evolution Algorithm for Constrained Optimization Problems [J].Journal of Software,2012,23(9):2374-2387.

[5] 刘大莲,徐尚文.求解约束优化问题的内外交叉遗传算法[J].系统工程理论与实践,2012,32(1):189-195. Liu Dalian,Xu Shangwen.Inward-outward Crossover Based Genetic Algorithm for Constrained Optimization Problem [J].System Engineering-Theory and Practice,2012,32(1):189-195.

[6] 龙文,梁昔明,徐松金,等.聚类佳点集交叉的约束优化混合进化算法[J].计算机研究与发展,2012,49(8):1753-1761. Long Wen,Liang Ximing,Xu Songjin,et al.A Hybrid Evolutionary Algorithm Based on Clustering good-point Set Crossover for Constrained Optimization[J].Journal of Computer Research and Development,2012,49(8):1753-1761.

[7]Homaifar A,Qi C X,Lai S H.Constrained Optimization Via Genetic Algorithms[J].Simulation,1994,62(4):242-254.

[8]周育人,李元香,王勇,等.Pareto强度值演化算法求解约束优化问题[J].软件学报,2003,14(7):1243-1249. Zhou Yuren,Li Yuanxiang,Wang Yong,et al.A Pareto Strength Evolutionary Algorithm for Constrained Optimization [J].Journal of Software,2003,14(7):1243-1249.

[9]Wang Y,Cai Z X.Combining Multiobjective Optimization with Differential Evolution to Solve Constrained Optimization Problems[J].IEEE Transactions on Evolutionary Computation,2012,16(1):117-134.

[10]Miettinen K.Nonlinear Multiobjective Optimization[M].Boston:Kluwer Academic Publishers,1999.

[11]Aguirre A H,Rionda S B,Coello C C A,et al.Handling Constraints Using Multiobjective Optimization Concepts[J]. International Journal for Numerical Methods in Engineering,2004,59(15):1989-2017.

[12]Tsutsui S,Yamamura M,Higuchi T.Multi-parent Recombination with Simplex Crossover in Real-coded Genetic Algorithms[C]//Proceedings of the Genetic and Evolutionary Computing Conference.San Francisco:Morgan Kaufmann Publishers,1999:657-664.

[13]Mezura-Montes E,Coello C C A.A Simple Multimembered Evolution Strategy to Solve Constrained Optimization Problems[J].IEEE Transactions on Evolutionary Computation,2005,9(1):1-17.

[14]Farmani R,Wright J A.Self-adaptive Fitness Formulation for Constrained Optimization[J].IEEE Transactions on Evolutionary Computation,2003,7(5):445-455.

(编辑:郭 华)

Multi-objective evolutionary algorithm based on preference for constrained optimization problems

DONG Ning1,WANG Yuping2

(1.School of Mathematics and Statistics,Xidian Univ.,Xi’an 710071,China; 2.School of Computer Science and Technology,Xidian Univ.,Xi’an 710071,China)

Constrained optimization problems(COPs)are converted into the bi-objective optimization problem and solved with a new preference based multi-objective evolutionary algorithm.A new hybrid crossover operator is proposed to improve the search ability in the evolutionary process,and also a novel fitness function with preference based on the achievement scalarizing function(ASF)which is used in the method of weighted metrics in multi-objective optimization is presented.The new fitness measures the merits of individuals by the weighting distance from individuals to the reference point,where the reference point and the weighting vector afford the preference for selection.In different evolutionary stages,the reference point and weighting vector are chosen adaptively according to the individuals in population to make a tradeoff between the preferences to the two objectives.Numerical experiments for several standard test functions with different characteristics illustrate that the new proposed algorithm is effective and efficient.

constrained optimization;multi-objective optimization;evolutionary algorithm;preference; achievement scalarizing function

TP301.6

A

1001-2400(2014)01-0098-07

10.3969/j.issn.1001-2400.2014.01.018

2012-10-16 < class="emphasis_bold">网络出版时间:

时间:2013-09-16

国家自然科学基金资助项目(61272119)

董 宁(1980-),女,西安电子科技大学博士研究生,E-mail:dongning@snnu.edu.cn.

http://www.cnki.net/kcms/detail/61.1076.TN.20130916.0926.201401.121_014.html