1 bit脉冲超宽带接收机采样抖动性能分析方法
张 超,岳光荣,尹华锐
(1.西安交通大学电信学院,陕西西安 710049;2.电子科技大学通信抗干扰技术国家重点实验室,四川成都 611731;3.中国科学技术大学电子工程与信息科学系,安徽合肥 230027)
1 bit脉冲超宽带接收机采样抖动性能分析方法
张 超1,岳光荣2,尹华锐3
(1.西安交通大学电信学院,陕西西安 710049;2.电子科技大学通信抗干扰技术国家重点实验室,四川成都 611731;3.中国科学技术大学电子工程与信息科学系,安徽合肥 230027)
为了准确评估1 bit脉冲超宽带接收机存在采样抖动时的性能,提出了一种基于中心极限定理的性能分析方法.首先将存在抖动的采样信号通过一阶泰勒展开为无抖动采样信号和采样抖动变量的线性函数,然后利用中心极限定理将接收机的判决变量建模为一个高斯分布的随机变量,从而得出接收机误码率表达式,最后根据采样抖动的随机分布模型,给出平均误码率上界表达式.该分析方法首次给出存在采样抖动时1 bit数字接收机性能的解析表达式,并且可用于其他线性干扰存在情况下的性能评估.实验结果表明,给出的平均误码率上界可以很好地反映接收机的实际性能,并且可用于高斯分布和平均分布两种随机采样抖动模型.
脉冲超宽带;采样抖动;数字接收机;中心极限定理
脉冲无线电超宽带技术(Impulse-Radio Ultra-WideBand,IR-UWB)利用低占空比的极窄脉冲作为载体传递信息,具有低成本、低功耗、低功率谱密度和高传输速率等优势,在高速无线互联、无线个域网和生物医疗传感网等方面有着广泛的应用前景[1].
由于IR-UWB脉冲信号持续时间极短,所以IR-UWB接收机对于采样定时抖动非常敏感.文献[2]首先对UWB系统采样定时抖动的影响进行了讨论,并发现采样定时严重影响着UWB系统的性能.文献[3]考察了定时抖动和信道估计误差均存在时,IR-UWB接收机可以取得的误码率.然而,以上的工作均基于传统的全精度接收(Full-Resolution,FR)技术,即认为采样点的量化是足够精确的.
随着应用场景的拓展,IR-UWB接收机在功耗、复杂度和体积等方面有着越来越高的要求.因此,目前主要考虑使用低功耗、低复杂度的有限精度数字接收技术[4].为了减少接收机模-数转换器的复杂度和功耗,文献[5]首先提出了1 bit量化的数字接收机思想,并设计了基于匹配滤波概念的接收算法.随后,文献[6]在1 bit采样量化的基础上提出了2 bit采样量化的接收机.文献[7]提出了基于1 bit采样量化的最优接收机算法,但是没有给出解析的接收机性能表达式.因为1 bit数字接收机以较低的复杂度和功耗,实现了接近传统全精度接收的性能[7-8],所以近来得到了较多的关注.文献[9]讨论了窄带干扰对1 bit数字接收机的影响,但是仍没有给出解析的性能表达式.文献[10-11]则讨论了1 bit接收机在测距和组网方面的应用.笔者从采样定时抖动入手,对1 bit IR-UWB数字接收机性能进行了分析,首次给出了存在采样抖动时1 bit数字接收机性能的解析表达式,而且该分析方法可用于其他线性干扰存在下的1 bit数字接收机的性能评估.
1 系统模型
1.1 1 bit数字接收机
考虑一个单用户的IR-UWB通信系统.设发射信号采用二进制幅度调制,

其中,k是发送符号标记;Ts是发送符号周期;dk∈{+1,-1},是发送的二进制符号;ptr(t)是发送脉冲波形.假设dk出现+1和-1的概率相同.考虑到信道估计的有效性,这里只讨论相干时间内的信道衰落情况,所以信道可以建模为线性时不变系统[6].设信道响应函数为h(t),那么接收信号r(t)=s(t)*h(t)+v(t).这里*为卷积运算符号,v(t)为双边带功率谱密度为N0/2的加性高斯白噪声.
1 bit数字接收机[7]的结构如图1所示.首先对接收到的信号进行低通滤波.考虑Ts足够大,因此不存在符号间干扰[6].设接收机低通滤波器为理想低通滤波prec(t)=(N0B)-1/2sin(2πBt)(πt),这里B为低通滤波器的带宽.那么接收波形可表达为pref(t)= ptr(t)*h(t)*prec(t).接收机接收的信号为
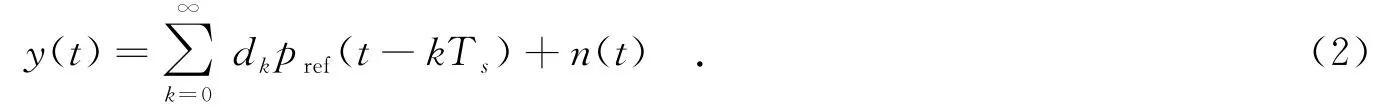

图1 1 bit接收机的结构
数字接收机对接收的波形进行采样,得到
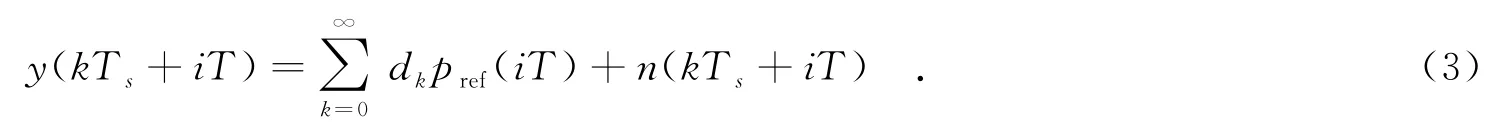
采样脉冲周期为T=1/(2B),每个脉冲信号周期内有N=T/Ts个采样点.这里n(kTs+iT)是均值为0、方差为N0/2的高斯噪声.
采样后,1 bit接收机对采样信号进行1 bit量化.因为发送符号由+1和-1组成,所以最佳的量化门限为0.第k个脉冲的第i个采样点1 bit量化结果为

在第k个符号dk的脉冲周期内,可以得到1 bit量化矢量信号[yk,0,yk,1,…,yk,N].所以1 bit最优数字接收机[]为

其中,wi为最优加权系数,其定义为

这里,εi为yk,i≠dk发生的概率.wi一般通过发射训练序列进行估计.首先对大量的训练序列进行过采样和1 bit量化,然后统计采样点是否与已知的发射符号相同,从而得出1 bit采样量化的错误概率εi.以上具体步骤请参见文献[7].笔者重点研究采样定时抖动对1 bit数字接收机的影响,为了简化研究目标,假设wi是精确已知的.
1.2 采样抖动模型
超宽带信号所需要的采样频率非常高,因此,对于模数转换器存在的采样抖动将会非常敏感.设第k个符号的第i个采样脉冲的采样定时抖动变量为δk,i,那么1 bit量化后的结果为

注意,此时采样点噪声n(kTs+iT+δk,i)服从均值为0、方差为N0/2的高斯分布.加权系数的估计虽然也存在采样抖动,但是估计εi时所用的采样点进行了大量的平均化运算,当训练序列足够多时,可以近似认为采样抖动对最优加权系数没有影响[3].因此,可以认为此时1 bit数字接收机的检测准则为

由于δk,i的绝对值往往很小,因此可以对pref(iT+δk,i)在iT处进行泰勒展开,
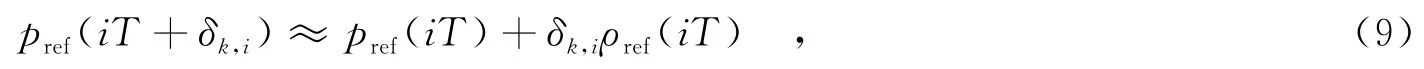
其中,ρref(iT)为pref(iT)的一阶导数.由于ptr(t)和prec(t)均已知,而h(t)可以通过训练序列进行估计.假设已经精确估计信道h(t),所以ρref(iT)也可以精确得到.记采样抖动失真项Δk,i=δk,iρref(iT),那么式(7)可写为

2 性能分析方法
2.1 确定性抖动分析
首先考虑N个采样点的采样抖动都是确定的.令yk=[y′k,0,…,y′k,N-1]T和w=[w0,…,wN-1]T.那么根据式(8),接收机判决变量为

因为dk取+1和-1的概率相同,所以接收机检测误码率(Bit Error Rate,BER)可以表示为

因为w是已知的,所以λk在dk=1时的概率分布由yk的概率分布决定.
由于使用了奈奎斯特采样频率,当采样抖动不存在时,各采样点之间是完全独立的[6],即对任意i≠j,n(kTs+iT)和n(kTs+jT)之间相互独立.对于存在抖动的情况,设v(t)为1 bit接收机的接收噪声n(t)的一阶导数,那么则有n(kTs+iT+δk,i)≈n(kTs+iT)+δk,iv(kTs+iT).所以可认为此时的采样点之间也相互独立,因此yk的各个分量之间也相互独立.首先考察dk=1时y′k,i的分布函数.因为每个采样点均服从均值为pref(iT)+Δk,i、方差为N0/2的高斯分布,所以y′k,i的概率分布函数为


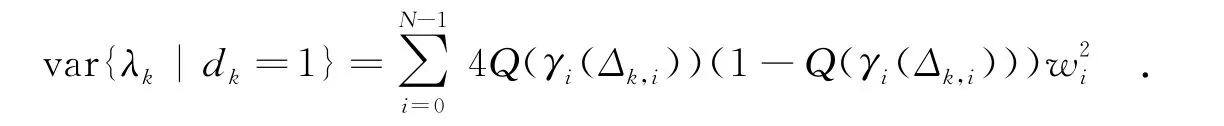
令qi=Q(γi(0)),则容易知道一般情况下,qi<0.5.考虑到当x→0时,有ln(1+x)≈x,那么加权系数wi可表达为
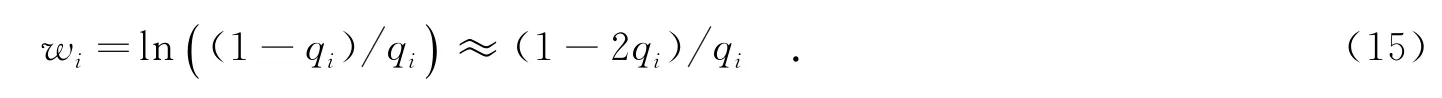
记γΔk,i=Δk,i,那么有

由于γΔk,i的取值非常小,因此可对Q(γi(Δk,i))在γi(0)处进行泰勒展开,即有


文献[6]证明了在使用高斯脉冲的IR-UWB系统中,即使有限精度量化采样点y′k,i之间的概率分布参数不同,接收机判决变量仍近似服从高斯分布.所以,式(12)所表示的误码率可计算为
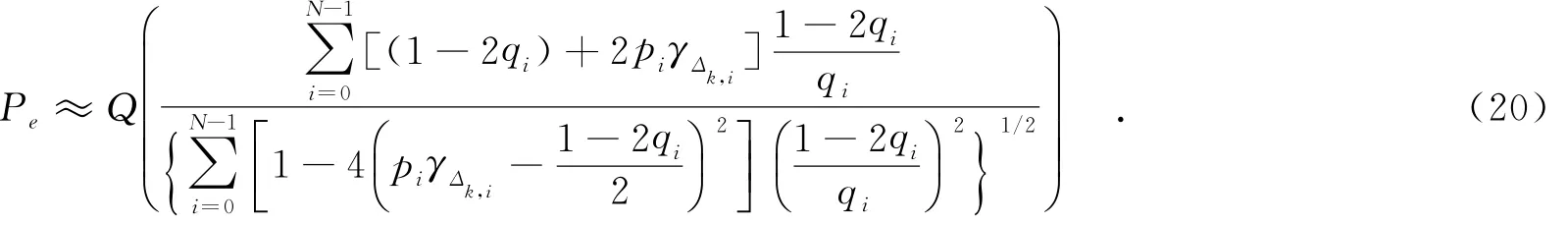
根据式(20),当没有采样抖动(即γΔk,i=0)时,1 bit IR-UWB数字接收机误码率为

2.2 随机性抖动分析
以上的分析过程均认为采样抖动是确定的,然而实际上采样抖动一般建模为一个平稳随机过程.这里使用最常用的随机抖动模型——高斯分布模型[3].需要说明的是,由于一个IR-UWB脉冲的持续周期非常短,所以可以合理地认为一个脉冲周期内的采样抖动是独立同分布的[3].
由于γΔk,i和pi都非常小,因此,可以认为

所以,式(21)可以进一步写为

采样抖动δk,i一般建模为均值为0、方差为的高斯分布.则 ,服从均值为0、方差为的高斯分布.因此,平均错误概率可计算为

由于式(24)不易直接计算,可考虑利用公式Q(x)≤exp(-x2/2)[12]计算平均误码率上界,即
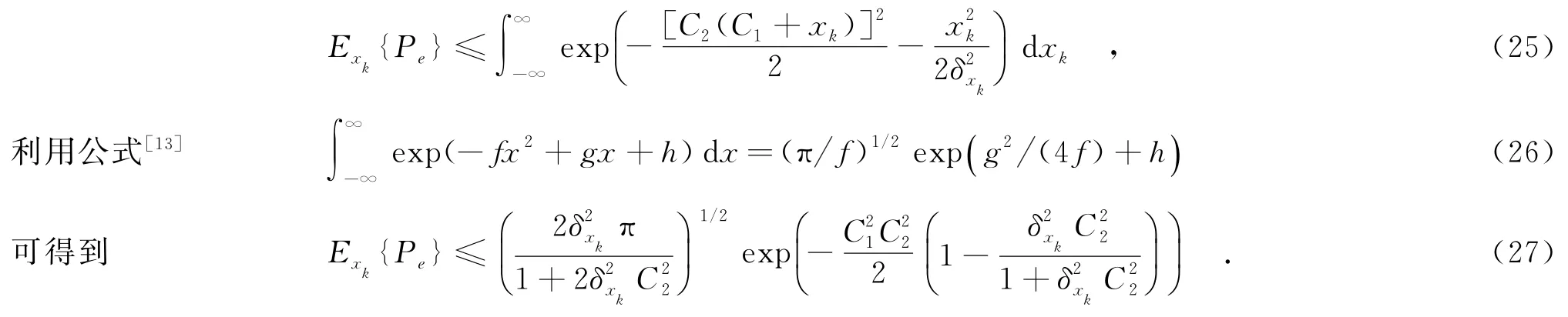
注意,式(27)仅是高斯随机抖动模型下1 bit接收机平均误码率的一个上界,但是其合理性在仿真实验中得到了验证.为了进一步挖掘文中分析方法的通用性和可靠性,对以下4种情况进行讨论:
(1)采样抖动服从其他分布的情况.考虑更通用的情况,采样抖动δk,i服从均值为0、方差为的任意分布时,根据中心极限定理,可近似认为xk仍服从均值为0、方差为的高斯分布.因此式(27)仍成立.例如,δk,i在区间[-A,A]上均匀分布[2],此情况将通过仿真实验验证.

可以看出,误码率随信号功率增加而产生的下降速率不再服从负指数规律,因而误码率下降速率非常缓慢.这说明采样抖动较大时,接收机将产生严重的性能下降.因此,1 bit数字接收机需要控制采样抖动.

可以看出,误码率随信号功率增加而产生的下降速率将服从负指数规律.实际情况下的采样抖动方差不会等于0,所以,不考虑等于0的情况.
(4)当信噪比较大时(γi(0)→∞).此时qi→0,pi→1/21/2.那么进一步有,和C2→0.因此,式(27)变为

很显然,式(29)和式(30)具有相同的指数项,这说明当信噪比增加到一定程度时,不同采样抖动下的误码率下降速率是相同的.因此,可以说明当信噪比较大时,不同的采样抖动只会引起误码率曲线的平移,不会影响曲线的斜率.
从以上的讨论中可以看到,文中不仅给出了1 bit IR-UWB数字接收机在存在采样抖动时的性能上界表达式,而且还为1 bit数字接收机的性能分析提供了一套较为完整的解决方法.例如,被采样信号中存在任意线性干扰信号时,均可以采用文中的分析方法给出性能上界.
3 仿真实验
通过计算机仿真对以上分析结果进行验证.使用二阶微分高斯脉冲作为发射信号,

其中取τ=0.16 ns以满足美国联邦通信委员会(FCC)对UWB信号的定义[9].使用标准CM1多径衰落信道模型[13].接收机理想低通滤波器带宽为8 GHz,采样周期为62.5 ps,脉冲发送速率为10M/s,高斯白噪声方差N0=1.式(27)是一次信道实现得到的平均误码率,实验中对式(27)的理论计算结果进行了1 000次信道实现平均.IR-UWB信号能量定义为

图2给出了采样抖动服从高斯分布时不同抖动均方根情况下的接收机误码率曲线.这里使用均方根表示采样抖动的大小.图2中不同的记号表示不同的采样抖动均方根情况下的仿真结果,实线则表示相应情况下理论误码率上界的计算结果.可以看到,所有的理论上界结果与实验仿真结果完全重合,因此,文中给出的误码率理论上界可以准确地反映出1 bit接收的误码率性能,可用于评估1 bit数字接收机的性能.当信噪比达到11 dB以上时,不同采样抖动下的误码率曲线斜率几乎一致,也验证了式(27)的讨论结果.观察同一误码率下的信噪比取值情况,例如误码率为10-5时,4 ps抖动下接收机比无抖动接收机需要0.8 dB左右的额外信噪比; 8 ps抖动下接收机比5 ps抖动下接收机需要0.1 dB额外信噪比;15 ps抖动下接收机比10 ps抖动下接收机需要0.1 dB额外信噪比.这说明当采样抖动变大时,性能损失增加的速率并没有增加.

图2 存在高斯分布采样抖动的1 bit接收机性能

图3 存在均匀分布采样抖动的1 bit接收机性能
图3给出了采样抖动服从均匀分布时不同采样抖动情况下的接收机误码率曲线.图3标记与图2完全一样.可以看到所有情况下的理论上界与仿真结果也基本一致.当抖动均方根较小时,例如4 ps,8 ps情况下,仿真结果略小于理论上界计算结果.这是因为均匀分布严格限制了抖动取值的范围,而高斯分布则可能使得抖动取值超过均匀分布的范围.因此,同样均方根情况下,均匀分布抖动引起的性能损失略小.当抖动均方根较大时,理论与仿真一致性较好.这也验证了结果讨论(1)的内容.
图4给出了全精度接收机和1 bit接收机在不同采样抖动情况下的性能.图中实线表示全精度接收机的性能,虚线表示1 bit接收机的性能.当没有采样抖动时,可以看到全精度接收比1 bit数字接收机有约2 d B的信噪比增益,这是由于1 bit量化引起的性能损失[7].当抖动均方差等于4 ps时,全精度接收机相对于无抖动情况会损失0.9 dB信噪比,而1 bit接收机则损失1 dB信噪比.这说明抖动均方根较小时,1 bit接收机比全精度接收机会产生更多的性能损失.但是,当抖动均方差为12 ps时,全精度接收机相对于无抖动情况会损失超过5 d B信噪比,而1 bit接收机则损失3.9 d B信噪比.这种情况在抖动均方根为20 ps时更加明显.这说明抖动均方根较大时,定时抖动对1 bit接收机的影响小于对全精度接收机的影响.
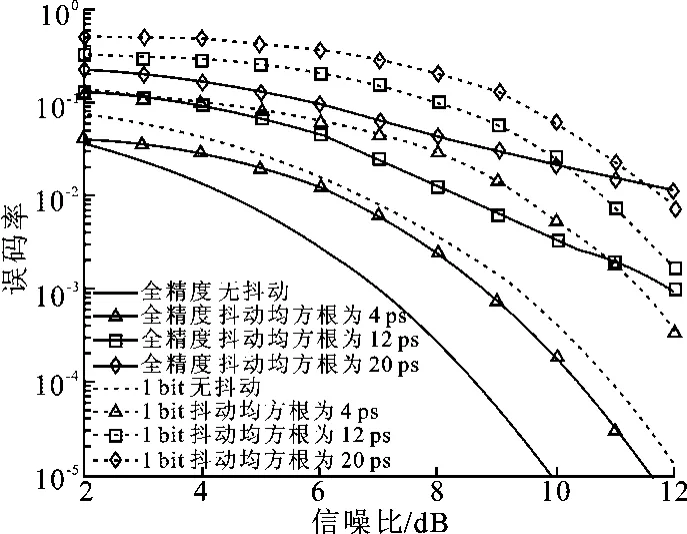
图4 相同采样抖动情况下全精度接收机和1 bit接收机的性能
4 结束语
综上所述,笔者提出的误码率上界能够很好地评估高斯随机抖动和均匀随机抖动情况下1 bit接收机的性能,所提出的分析方法可以用于其他情况下评价1 bit接收机的性能.从结果来看,相同的干扰强度,1 bit接收机的性能不一定比全精度接收机的差,强度较小的抖动对于1 bit接收机影响较大,但是强度较大的抖动对于1 bit接收机反而小于对于全精度接收机的影响.这个结果进一步丰富了1 bit接收机的理论和应用.
[1]Akyildiz I F,Melodia T,Chowdury,K R.Wireless Multimedia Sensor Networks:a Survey[J].IEEE WirelessCommunications,2007,14(6):32-39.
[2]Lovelace W M,Townsend J K.The Effects of Timing Jitter and Tracking on the Performance of Impulse Radio[J]. IEEE Journal of Selected Areas in Communications,2002,20(9):1646-1651.
[3]Fort A,Chen M,Desset C.Impact of Sampling Jitter on Mostly—Digital Architectures for UWB Biomedical Applications[C]//Proceedings of IEEE International Conference on Communications.Piscataway:IEEE,2007:5769-5774.
[4]Tang Jin,Xu Zhengyuan,Sadler B M.Performance Analysis of b-bit Digital Receivers for TR-UWB Systems with Inter-Pulse Interference[J].IEEE Transactions on Wireless Communications,2007,6(2):494-505.
[5]Hoyos S,Sadler B M,Arce G R.Monobit Digital Receivers for Ultra-wideband Communications[J].IEEE Transactions on Wireless Communications,2005,4(4):1337-1344.
[6]Ke Lei,Yin Huarui,Gong Weilin.Finite-resolution Digital Receiver Design for Impulse Radio Ultra-wideband Communication[J].IEEE Transactions on Wireless Communications,2008,7(12):5108-5117.
[7]Yin Huarui,Wang Zhengdao,Ke Lei.Monobit Digital Receivers:Design,Performance,and Applications to Impulse Radio[J].IEEE Transactions on Communications,2010,58(6):1695-1704.
[8]Gong Weilin,Yin Huarui,Ke Lei.Performance Analysis of IR-UWB 1 bit Digital Receivers[C]//Proceedings of IEEE Conference on Information Science and Systems.Piscataway:IEEE,2010:897-901.
[9]Zhang Chao,Yin Huarui,Ren Pinyi.The Effects of Narrowband Interference on Finite-Resolution IR-UWB Digital Receivers[J].IEEE Communications Letters,2011,15(5):536-538.
[10]Sun Fei,Yin Huarui,Wang Weidong.Finite-Resolution Digital Receiver for UWB TOA Estimation[J].IEEE Communications Letters,2012,16(1):76-79.
[11]Chen Xiaohui,Xu Sheng,Yin Huarui,et al.Potentials of IR-UWB Technology for Ubiquitous Computing[J].Personal and Ubiquitous Computing,2011,15(1):75-84.
[12]Gold S A.Wireless Communications[M].Cambridge:Cambridge University Press,2005.
[13]Gradshteyn I S,Ryzik I M.Table of Integrals,Series,and Products[M].7ed.Amsterdam:Elsevier,2007.
[14]Forester J.Channel Modeling Sub-committee Report Final[R/OL].[2012-08-08].http://grouper.ieee.org/groups/ 802/15/pub/2003/Mar03/02490r1P802-15_SG3a-Channel-Modeling-Subcommittee-Report-Final.zip.
(编辑:李恩科)
Novel method for analyzing the performance of the 1 bit IR-UWB receiver in the presence of timing jitter
ZHANG Chao1,YUE Guangrong2,YIN Huarui3
(1.School of Electronic and Information Engineering,Xi’an Jiaotong Univ.,Xi’an 710049,China;2. National Key Lab.of Communications,Univ.of Electronic Science and Technology of China,Chengdu 611731,China;3.Dept.of Electronics Engineering&Information Science,Univ.of Science and Technology of China,Hefei 230027,China)
A novel method based on the Central Limit Theorem(CLT)is proposed to analyze the performance of the 1 bit Impulse-Radio Ultra-WideBand(IR-UWB)receiver in the presence of a timing jitter.First,the sampled signal with timing jitter is expressed as a linear function of the sampled signal without jitter and timing jitter through first-order Taylor series expansion.Then by the CLT,the decision variable of the 1 bit receiver is considered as Gaussian distributed and the bit error rate(BER)is derived. After that,an upper bound of the averaged BER is also provided based on the distribution of random timing jitter.The given analytical result is the first analytic expression of the BER performance of the 1 bit receiver with timing jitter and can be used for the case where the 1 bit receiver has a linear interference. Experimental results show that the proposed upper bound agrees with the actual performance of the 1 bit receiver very well and can be used for both Gaussian distributed and uniform distributed timing jitter.
impulse-radio ultra-wideband(IR-UWB);timing jitter;digital receiver;central limit theorem
TN914.42
A
1001-2400(2014)01-0140-07
10.3969/j.issn.1001-2400.2014.01.025
2012-10-16 < class="emphasis_bold">网络出版时间:
时间:2013-09-16
国家自然科学基金资助项目(61102082,60802008);教育部博士点基金资助项目(20110201120011)
张 超(1982-),男,讲师,博士,E-mail:chaozhang@mail.xjtu.edu.cn.
http://www.cnki.net/kcms/detail/61.1076.TN.20130916.0926.201401.174_021.html

