避免非视距影响的蒙特卡罗移动节点定位方法

阔永红,周文文,陈 健

(西安电子科技大学通信工程学院,陕西西安 710071)

避免非视距影响的蒙特卡罗移动节点定位方法

阔永红,周文文,陈 健

(西安电子科技大学通信工程学院,陕西西安 710071)

为避免引入移动传感器网络中受到非视距影响的信息,提出了基于节点一跳邻居的广播信息进行定位的算法,采用信息洪泛的方式来提高节点的利用效率.在采样阶段,将已定位节点作为虚拟锚节点,并优化已定位节点邻居的采样箱,提高在低锚节点密度下的定位精度;在滤波阶段,利用连通性理论和未知节点的位置信息改进滤波条件,提高节点的采样效率;利用虚拟锚节点一跳信息逐层实现网络所有节点的定位.仿真结果表明,无论有无障碍物,该算法与传统算法相比,定位精度均得到提高,尤其在低锚节点密度的网络中具有较好的定位效果.

无线传感器网络;节点定位;蒙特卡罗算法;虚拟锚节点;采样;过滤

在无线传感器网络的各种应用中,监测到事件后就需要确定事件的发生位置,因此节点自身的准确定位对无线传感器网络的应用有着重要的意义.无线传感器网络自身定位方法有两种机制,分别是基于测距的机制和无须测距的机制.基于测距的定位机制需要测量未知节点与锚节点之间的距离或角度信息,有基于到达角(Angle Of Arrival,AOA)、到达时间(Time Of Arrival,TOA)[1]、接收信号强度(Received Signal Strength Indicator,RSSI)[2]的定位等;而无须测距的定位机制仅根据网络的连通性等信息实现节点的定位,有质心法[3]、距离向量算法(Distance Vector Hop,DV-Hop)[4]、基于采样的定位方法[5]等.

以上算法适用于静止传感器网络.在移动环境中,网络结构与节点间拓扑约束关系不断变化,算法的定位精度急剧下降,如何利用节点移动信息提高定位精度成为一个热点问题.文献[6]提出蒙特卡罗定位(Monte Carlo Localization,MCL)算法,为无线传感器移动节点的定位开辟了新径;文献[7-8]采用蒙特卡罗箱(Monte Carlo Boxed,MCB)算法,通过建立采样箱提高节点采样效率;文献[9]将距离向量算法与蒙特卡罗定位算法相结合来提高定位精度;文献[10-11]应用测距信息提高蒙特卡罗定位算法的定位精度.在视距环境下,蒙特卡罗定位、蒙特卡罗箱等算法利用锚节点的广播信息进行定位并达到了较高的精度;但在非视距环境下,障碍物可能对锚节点二跳邻居节点的定位产生负面信息,算法将产生较大的定位误差.

针对上述问题,笔者研究了一种避免非视距影响的移动节点定位算法——EMCB(Enhanced Monte Carlo Boxed),采用一跳邻居洪泛信息进行定位,改进采样与过滤方法,避免了非视距的影响,克服了二跳负面信息引起的定位误差.将已定位节点转化为虚拟锚节点,增加了一跳定位信息,提高了算法在低锚节点密度网络中的定位精度;利用连通性理论和未知节点的位置信息强化滤波条件,提高节点的采样效率;利用虚拟锚节点广播的信息,逐层定位网络内的所有节点.

1 蒙特卡罗箱算法描述

蒙特卡罗箱算法中未知节点利用其一跳、二跳通信范围内的锚节点广播的信息进行定位,其过程由采样阶段与过滤阶段构成,如图1所示.

图1 t时刻节点的定位流程图

1.1 采样阶段

假设未知节点为A,图2中阴影部分为节点A可能所在的区域,Vmax为节点最大运动速度,P点为节点A在t-1时刻的位置,R为节点的通信半径,s1、s2为节点A的锚节点.图2(d)中阴影区域为节点A、s1的一跳通信范围和s2的二跳通信范围的交集.由于阴影区域不规则,为了方便计算,取各圆外接矩形的重叠区域作为采样箱,节点可在采样箱中随机采样.

图2 蒙特卡罗箱算法

1.2 过滤阶段

由图2(d)可以看出,由于采样箱用矩形表示,矩形区域大于节点的预测区域,因此随机采样时可能取到无效的采样点,需要对采样点进行过滤.

l表示未知节点的采样点,确定有效采样点集合O的条件为

其中,S1、S2分别表示未知节点的一、二跳锚节点集合,R表示节点的通信半径,d表示距离.

1.3 蒙特卡罗箱算法存在的问题

在理想情况下,蒙特卡罗箱算法可以达到较高的定位精度,但实际存在的障碍物可能使得二跳通信范围内的锚节点广播的信息成为负面信息,如图3所示.

图3中s1为锚节点,A、B、C、D为可相互通信的未知节点,且A、B节点与s1可以直接通信,D可以通过A或B与s1间接通信.由于存在障碍物,C与s1无法直接通信,也需通过A或B与s1间接通信,因此s1错将C当成二跳邻居,采样区域由s1的一跳通信区域变成了s1的二跳通信区域,见图3中的阴影部分,将出现较大的定位误差.

图3 负面信息效果图

2 EMCB算法

2.1 定位思想

为解决1.3节所述问题,考虑仅利用一跳邻居广播的信息对节点进行定位.但在低锚节点密度网络中,大部分节点不是一跳锚节点的邻居,采样箱需扩展到整个通信区域,导致误差不可控制.为了增加节点可利用信息量,EMCB算法将已定位节点作为虚拟锚节点,逐层完成节点的定位.图4给出了以一个锚节点为中心的多层定位示意图.

由锚节点开始,首先对锚节点可直接通信的节点(图4中第1层节点)进行定位,然后第1层节点转化为虚拟锚节点,对其可直接通信的节点(图4中第2层节点)进行定位,依次向外延伸,各节点逐层定位.

EMCB算法仍由采样阶段与过滤阶段构成,如图5所示.

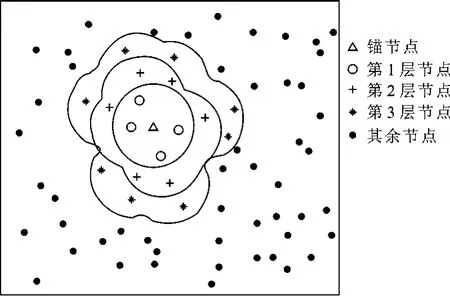
图4 逐层定位图示

2.2 采样阶段

所有节点采用受控的洪泛方式向其一跳邻居发送信息.由于虚拟锚节点自身定位存在误差,故在EMCB算法中锚节点广播当前时刻自身的位置,虚拟锚节点向邻居广播其采样箱的位置,每个未知节点分两个阶段确立采样箱,而后在其采样箱内随机采样.

图5 EMCB算法流程图

2.2.1 第1层节点采样箱的确立

由于锚节点与虚拟锚节点广播的信息不同,故第1层与其余层节点采样箱确立过程不同,如图6所示.

图6(a)中第1层节点A利用锚节点s1、s2的一跳通信范围确定重叠区域作为初步采样箱,类似于蒙特卡罗采样箱确立过程(见图2).图6中的参数如下:

图6 第1层节点确立采样箱

其中,(xj,yj)为节点A的一跳锚节点的坐标,为节点A在时刻t-1的采样值,R为节点的通信半径,Vmax为节点最大运动速度.

节点A、B彼此优化采样箱,见图6(b)所示.当A、B已经确定初步采样箱时,广播自身的采样箱信息.A收到B的广播信息,并确定A在B的通信范围内.由于B的真

实位置是其初步采样箱内的某一点,则A节点必然在包含B初步采样箱所有可通信范围的正方形区域B1B2B3B4内.取B1B2B3B4与A的初步采样箱的交集得到A的最终采样箱,即图6(b)中阴影区域,采样箱区域位置(xAmin,xAmax,yAmin,yAmax)为

B的最终采样箱确立与上述过程相同,这样就确定了第1层节点的采样箱.

2.2.2 其余层节点的采样箱的确定

每层节点定位以后转化为虚拟锚节点.由于定位存在误差,如果由其预测位置坐标确定下一层节点的采样箱,误差累计迅速增大,因此,每层节点向其邻居广播其采样箱信息,它们采样箱的确立如图7所示.

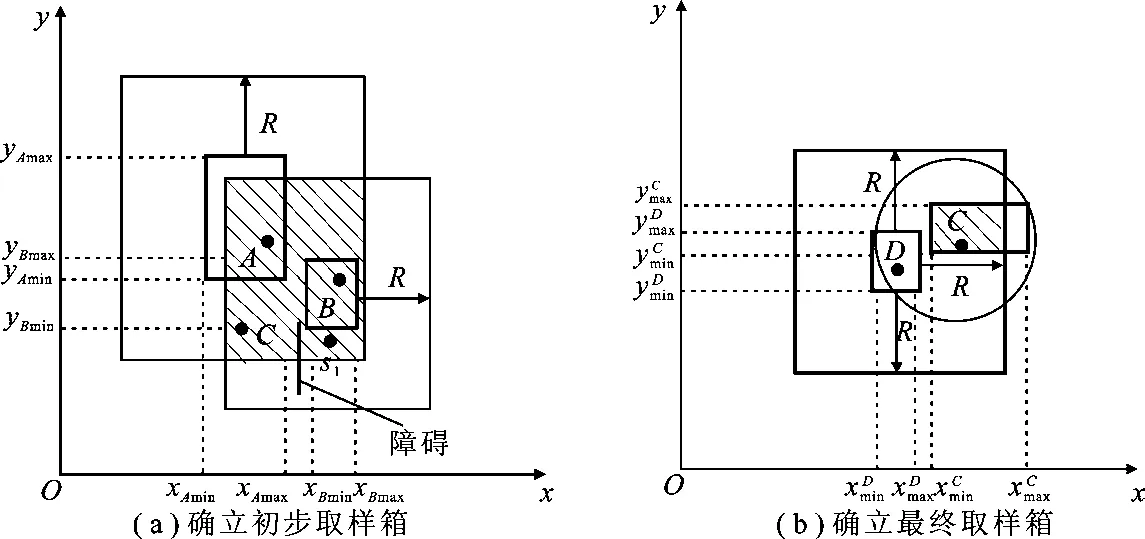
图7 其余层节点确立采样箱

由于存在障碍物,C由第1层节点变为第2层节点,其虚拟锚节点为第1层节点A、B,则C的初步采样箱为图7(a)中阴影区域,它的采样箱为

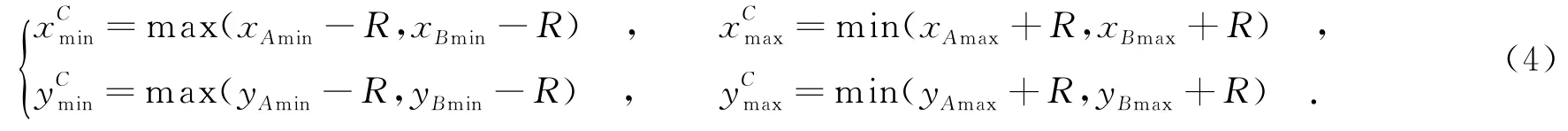
D为第2层节点,同样也利用其第1层虚拟锚节点确立初步采样箱节点C、D彼此优化初步采样箱的过程与第1层节点的相同,节点C确立最终采样箱见图7(b)阴影部分.其余层节点确立采样箱的过程与第2层节点的相同.在定位过程中,采样箱可能产生坐标冲突或在通信范围外,这时候重置采样箱于初步状态或整个通信区域.

2.3 过滤阶段

EMCB算法不仅利用式(1)的约束条件进行过滤,还利用节点连通性限制理论过滤采样点,利用未知节点的位置信息预测节点当前时刻所在的区域,提高采样效率.

2.3.1 连通性限制理论过滤采样点

如图8所示,假设阴影区域C(z)内不存在节点C的邻居,则节点C从Ct-1移动到Ct,连通性不发生改变.

反之,若节点C移动时连通性不变,移动最大距离z[12]必须确保阴影区内不存在C的邻居,此时,

图8 连通性理论限制图

2.3.2 运动区域过滤采样点

在实际应用中,节点在短时间内运动方向一般改变不大.笔者利用节点前两个时刻的预测位置连线预测当前时刻的运动方向[13].

如图9所示,假设Ct-1、Ct-2为未知节点C在t-1、t-2时刻的预测位置.在t时刻,节点C沿大于沿其他方向移动的概率.但由于Ct-1、Ct-2存在误差,所以节点C在t时刻的运动方向加入松弛角度Δφ,即如果的运动方向为θ,则C当前时刻的运动方向区域为[θ±Δφ].

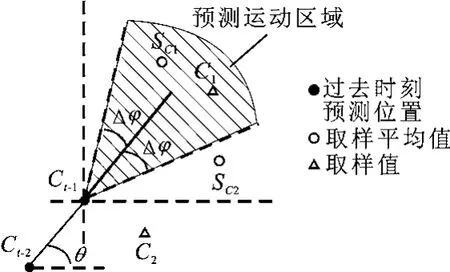
图9 运动区域约束示意图

移动节点随时可能改变其运动方向,所以上述预测约束方法仅在以下条件下使用:当采样平均值SC位于预测运动区域内时,说明当前时刻节点的运动与前两个时刻的运动相关性高,如图9中SC1,此时运动区域约束适用,把不在阴影区域内的采样值C2过滤掉,保留在区域内的采样值C1.当采样平均值SC不在预测运动区域内时,如图9中SC2,此区域预测不成立.

随着松弛角度增大,运动方向约束区域变大,许多不合理采样点仍然存在,如Δφ为180°时,此过滤阶段无过滤无效点的作用;当松弛角度较小时,由于运动方向约束区域很小,会过滤掉许多有效采样值点.引入精度提高的定义[13],其中E表示在不同的松弛角度下提高的精度:

图10给出了Δφ在[15°,180°]之间改变对精度提高的影响.由图可见,当Δφ为45°时,定位精度最高.因此在定位过程中取Δφ=45°.

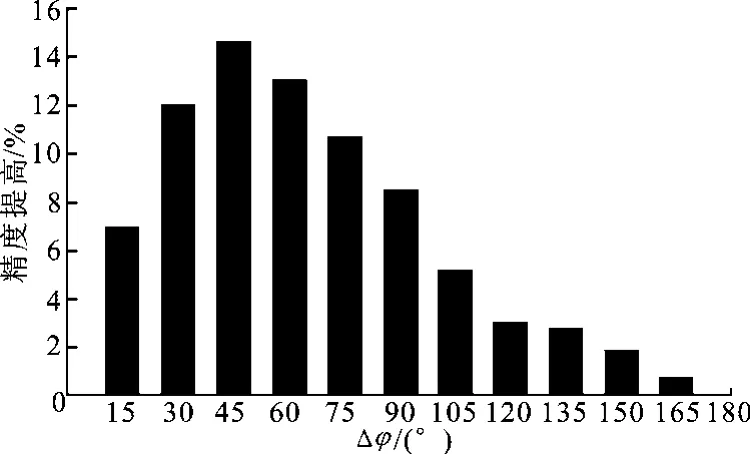
图10 松弛角度Δφ对算法的影响

3 性能仿真与分析

仿真环境为500 m×500 m的矩形区域,节点总数为350,锚节点密度为8%.所有节点的射频通信半径R均为50 m,且均以[0,Vmax]的速度移动,最大移动速度Vmax=R,所有节点均按照随机路点[14]移动模型运动.图11研究了EMCB算法与蒙特卡罗定位、蒙特卡罗箱算法的收敛性,以及定位误差与锚节点密度、节点运动速度、未知节点数目、节点通信不规则度(半径不规则度D)、非视距影响(非视距影响概率ρ)的关系.

3.1 算法的收敛性

图11(a)表明了3种算法随着时间变化的定位误差.由仿真结果可看出,3种算法定位误差都逐渐下降,经过5 s后,定位误差趋于稳定.EMCB算法整体优于蒙特卡罗定位、蒙特卡罗箱算法,在最好情况下,定位误差提高了0.1R.

3.2 锚节点密度对算法性能的影响

仿真过程中节点总数为350,节点最大移动速度Vmax=R,锚节点密度从1%变至15%,3种算法性能如图11(b)所示.随着锚节点密度增大,未知节点接收到更多的锚节点位置信息,从而减小了采样箱面积,因此3种算法的定位精度都逐渐提高,且定位精度差距也在减少.但在低锚节点密度网络中(1%),EMCB算法定位误差约为蒙特卡罗箱算法的40%,定位精度明显提高.

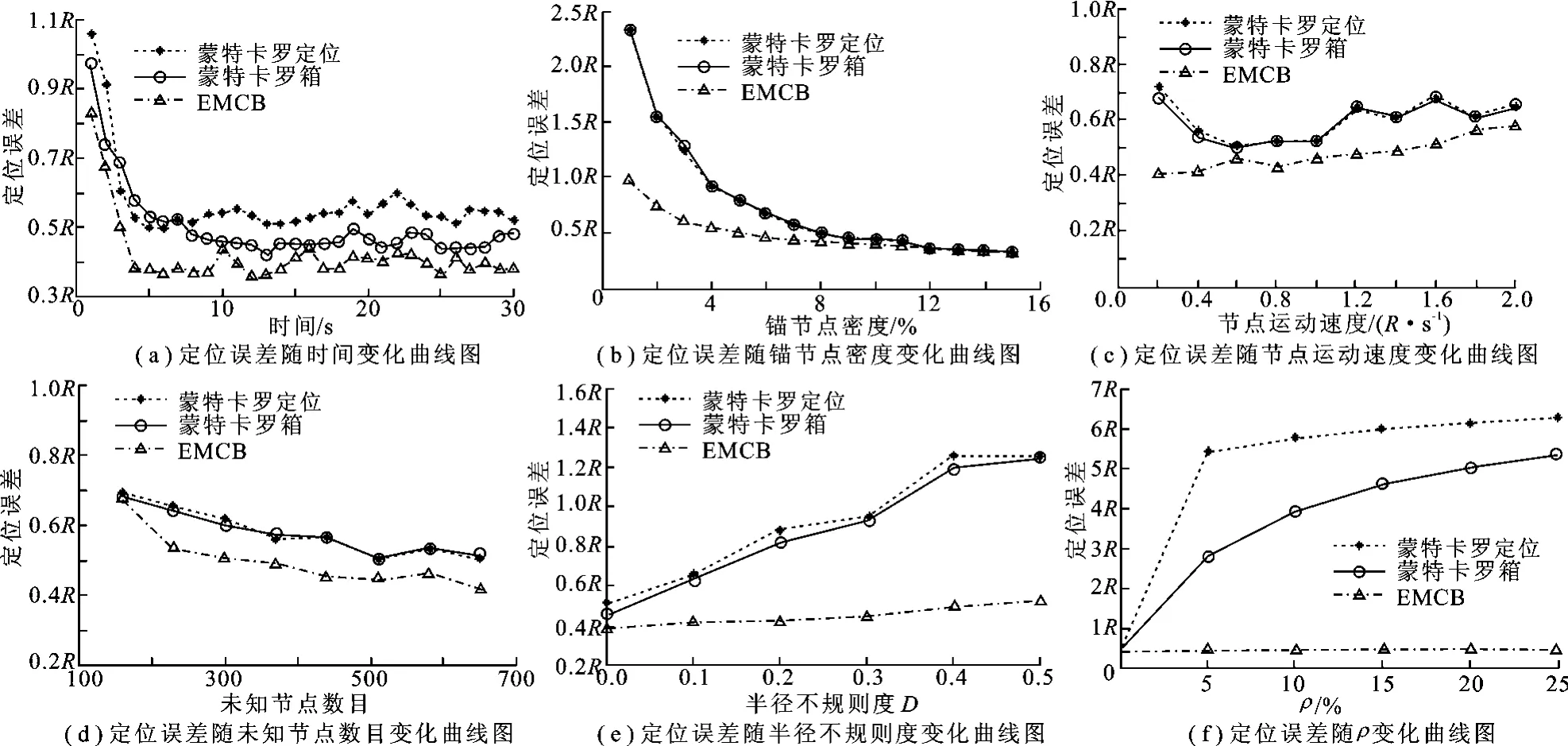
图11 定位误差变化曲线图

3.3 节点移动速度对算法性能的影响

仿真过程中节点总数为350,锚节点密度为8%,运动速度从0.2R变至2R.图11(c)表明,当节点运动速度很慢时,EMCB算法定位精度比蒙特卡罗箱算法提高了约0.3R.随着节点运动速度的增大,EMCB算法定位误差增大,但仍比蒙特卡罗箱、蒙特卡罗定位算法约低0.1R.因此,EMCB算法比蒙特卡罗定位、蒙特卡罗箱算法更适合拓扑结构变化稍快的网络.

3.4 未知节点密度对算法性能的影响

仿真过程中锚节点数目为28,节点最大移动速度Vmax=R.改变未知节点数目,观察其对算法性能的影响,同时节点总数也发生改变,仿真结果如图11(d)所示.当未知节点密度较低时,各算法的定位精度相近.随着未知节点数目增大,EMCB算法比蒙特卡罗定位、蒙特卡罗箱算法的精度约提高0.1R.蒙特卡罗定位、蒙特卡罗箱算法虽然仅应用一跳、二跳锚节点的位置信息,但未知节点数目增大时,未知节点的二跳锚邻居也可能增多;而EMCB算法将已定位节点转化为虚拟锚节点,充分地利用了未知节点,因此增加未知节点数目有利于提高算法的定位精度.

3.5 节点半径不规则度对算法性能的影响

在实际应用环境中,无线传感器网络中节点的通信半径会受到很多环境因素的影响.为了更逼近于实际环境,笔者引入通信半径不规则度D.节点的通信半径在[(1-D)×R,R]内随机选择.若D=0.2,则表示节点通信半径在[0.8R,R]内随机选择.仿真过程中节点总数为350,锚节点密度为8%,最大运动速度Vmax=R,参数D从0变到0.5,3种算法的性能如图11(e)所示,它们的平均定位精度都随着节点通信半径不规则度的增大而降低.D对蒙特卡罗定位、蒙特卡罗箱算法影响较大.当D＞0.3时,两种算法的定位误差超过R,已经不能满足普通网络的定位精度要求;而EMCB算法的平均定位精度下降缓慢(小于0.6R),可以满足普通网络的定位精度要求.

3.6 非视距影响对算法性能的影响

仿真过程中节点总数为350,锚节点密度为8%,最大运动速度Vmax=R.节点之间的通信是否受到非视距影响为随机的,笔者设置参数ρ表示非视距影响概率(仅考虑对定位影响比较大的非视距影响,如图3所示).若ρ=5%,则表示5%的一跳锚节点由于非视距影响,被未知节点当做二跳锚节点.ρ从0%变到25%,观察3种算法的性能.

由图11(f)可以看出,在非视距环境下,随着ρ的提高,蒙特卡罗定位、蒙特卡罗箱算法的定位精度急剧下降(达到5R以上,意味着定位出现严重错误),而EMCB算法的平均定位精度远在蒙特卡罗定位、蒙特卡罗箱算法之上,维持在0.4R左右.随着ρ的提高,EMCB算法变化不大,这是由于EMCB算法定位中可用信息比较多,ρ值的提高等价于锚节点密度的下降,虽然定位精度下降,但不会出现蒙特卡罗定位、蒙特卡罗箱算法的定位错误情况.

4 总 结

笔者提出了一种适用于非视距条件下的移动无线传感器网络的移动节点定位算法.仿真结果表明:在节点通信受到非视距的影响情况下,原始算法定位错误,而EMCB算法定位仍然较为准确;在无障碍物环境下,EMCB算法的定位精度优于原始算法的定位精度.另外,EMCB算法还可以应用在网络锚节点密度低的场合,定位精度受通信半径不规则度影响小.

[1]Xu Enyang,Ding Zhi,Dasgupta S.Source Localization in Wireless Sensor Networks from Signal Time-of-Arrival Measurements[J].IEEE Transactions on Signal Processing,2011,59(6):2887-2897.

[2]Salman N,Ghogho M,Kemp A H.On the Joint Estimation of the RSS-Based Location and Path-Loss Exponent[J]. IEEE Wireless Communications Letters,2012,1(1):34-37.

[3]Wang Jun,Urriza P,Han Yuxing,et al.Weighted Centroid Localization Algorithm:Theoretical Analysis and Distributed Implementation[J].IEEE Transactions on Wireless Communications,2011,10(10):3403-3413.

[4]Agashe A A,Patil R S.An Optimum DV Hop Localization Algorithm for Variety of Topologies in Wireless Sensor Networks[J].International Journal on Computer Science and Engineering,2012,4(6):957-961.

[5] 程伟,史浩山,李冬.无线传感器网络中的进化规划重采样定位算法[J].西安电子科技大学学报,2011,38(4):154-159. Cheng Wei,Shi Haoshan,Li Dong.Novel Localization Algorithm Based on Evolutionary Programming Resampling in WSN[J].Journal of Xidian University,2011,38(4):154-159.

[6]Hu Lingxuan,Evans D.Localization for mobile sensor networks[C]//International Conference on Mobile Computing and Networking.Piscataway:IEEE,2004:45-57.

[7]Baggio A,Langendoen K.Monte Carlo Localization for Mobile Wireless Sensor Networks[J].Ad Hoc Networks,2008,6(5):718-733.

[8]Soltaninasab B,Sabaei M,Amiri J.Improving Monte Carlo Localization Algorithm Using Time Series Forecasting Method and Dynamic Sampling in Mobile WSNs[C]//International Conference on Communication Systems Networks and Applications.Piscataway:IEEE,2010:389-396.

[9]Yi J Y,Yang S W,Cha H J.Multi-hop-based Monte Carlo Localization for Mobile Sensor Networks[C]//4th Annual IEEE Communications Society Conference on Sensor,Mesh and Ad Hoc Communications and Networks.Piscataway: IEEE,2007:163-171.

[10]Wang W D,Zhu Q X.RSS-based Monte Carlo Localization for Mobile Sensor Networks[J].IET Communications,2008,2(5):673-681.

[11]Shao Qingliang,Xu Hongyu,Liang Jia,et al.The Research of Monte Carlo Localization Algorithm Based on Received Signal Strength[C]//International Conference on Wireless Communications,Networking and Mobile Computing. Piscataway:IEEE,2011:1-4.

[12]Radhika N,Howard S,Jonathan B.Organizing a Global Coordinate System from Local Information on an Ad Hoc Sensor Network[C]//2nd International Workshop on Information Processing in Sensor Networks.Berlin:Springer-Verlag,2003:333-348.

[13]Sheu Jangping,Hu Weikai,Lin Jenchiao.Distributed Localization Scheme for Mobile Sensor Networks[J].IEEE Transactions on Mobile Computing,2010,9(4):516-526.

[14]Vasanthi V,Romen Kumar M,Ajith Singh N.A Retailed Study of Mobility Models in Wireless Sensor Network[J]. Journal of Theoretical and Applied Information Technology,2011,33(1):7-14.

(编辑:郭 华)

Monte Carlo mobile node localization for NLOSenvironment

KUO Yonghong,ZHOU Wenwen,CHEN Jian
(School of Telecommunication Engineering,Xidian Univ.,Xi’an 710071,China)

Enhanced Monte Carlo Boxed(EMCB),based on the broadcasting messages of one-hop neighbor nodes,is proposed in a mobile wireless sensor network for NLOS environment.The utilization efficiency of nodes is improved in the way of message flooding.The located nodes are used as the virtual anchor nodes in order to improve the location precision in the network with few anchors,optimizing the sample boxes of the neighbor nodes.Besides,both the theoretical limit of connectivity and the previous location information are used to enhance the filtering performance.Taking advantage of the one-hop messages,all the nodes are located layer-by-layer.Finally,the results of simulation show that the location precision is improved compared with the traditional algorithms in any situation.Especially,a good performance is achieved with fewer anchor nodes.

wireless sensor network;node localization;Monte Carlo algorithm;virtual anchor nodes; sampling;filtering

TP393

A

1001-2400(2014)01-0006-07

10.3969/j.issn.1001-2400.2014.01.002

2012-11-01 < class="emphasis_bold">网络出版时间:

时间:2013-09-16

国家自然科学基金资助项目(60972072,61340033);高等学校学科创新引智计划资助项目(B08038)

阔永红(1967-),女,教授,E-mail:yhkuo@mail.xidian.edu.cn.

http://www.cnki.net/kcms/detail/61.1076.TN.20130916.0926.201401.8_032.html