短突发传输系统的联合导频和迭代译码载波同步
孙锦华,王雪梅,吴小钧
(1.西安电子科技大学综合业务网理论及关键技术国家重点实验室,陕西西安 710071; 2.长安大学信息工程学院,陕西西安 710064)
短突发传输系统的联合导频和迭代译码载波同步
孙锦华1,王雪梅1,吴小钧2
(1.西安电子科技大学综合业务网理论及关键技术国家重点实验室,陕西西安 710071; 2.长安大学信息工程学院,陕西西安 710064)
针对短突发通信在低信噪比条件下的载波同步算法存在估计精度低和同步范围小的问题,提出了联合导频和迭代译码的载波同步算法.首先对导频序列的去调制信息进行互相关,并利用互相关之和对载波参数进行粗估计;然后再重新利用导频序列和扩展Turbo译码器输出的信息位和校验位的软信息进行载波参数的细估计,进而实现有效的载波同步.理论分析和仿真结果表明,粗估计算法能够兼顾频率估计范围和估计精度的要求,针对一定长度的数据序列,Preamble-Middle结构是最优的帧结构;当归一化频偏小于1.5×10-3时,通过粗同步,使得Turbo码在剩余频偏范围内输出软信息比较可靠,再结合译码器输出的软信息进行细估计,使得Turbo码能够达到理想的误码率性能.
同步;导频;Turbo码;软输出
近年来,Turbo码、LDPC(Low Density Parity Check)码等香农极限码的性能一直受到广泛的关注,但其编码增益高、工作信噪比门限低等优异的性能只有在精确同步的条件下才能体现出来.尤其是在低信噪比条件下,短突发通信能否有效地进行,载波同步是首要解决的问题.
像Kay、Fitz、L&R、最大似然估计[1-2]等传统的数据辅助的载波同步算法是通过增加导频序列的长度来提高载波估计精度的,因此不适合短突发通信系统.近年来,针对迭代接收机提出的编码辅助的载波同步算法[3-10]在低信噪比下的估计性能获得了较大的改进.有许多研究表明,利用香农极限码的结构特点,将译码和同步相结合,可以显著地提高载波同步参数的估计性能.文献[3]针对Preamble-Postamble(PP)结构和Preamble-Middle(PM)结构提出了一种基于导频互相关和期望最大化算法的载波同步方案,该算法只能校正较小范围的频偏(ΔfTs≤6×10-4).文献[6]提出的最大似然联合迭代软判决引导的载波同步算法(MLISDD),利用周期图谱峰结合Turbo译码软信息改善低信噪比下的载波同步性能.首先粗估计部分利用导频基于最大似然估计算法对频率进行粗搜索,然后细估计部分利用经过非线性变换的Turbo译码输出的软信息基于最大似然估计算法对频率进行细搜索.仿真结果表明,对于10°以内的相位抖动和较小的频偏(ΔfTs≤7×10-4),仅需要22个导频比特估计性能就能达到克拉美罗界[11].但当频偏ΔfTs>7×10-4时,由于导频数目有限,经过粗估计后的剩余频偏达不到Turbo译码的要求,由此得到的译码软信息可靠性很差,即使通过多次迭代译码仍无法提高软信息的可靠性.另外,粗估计和细估计都是基于最大似然估计算法进行频率搜索,同时细估计部分还需要对译码软信息进行非线性变换,在一定程度上导致ML-ISDD算法比较复杂.在文献[7]中,最大似然迭代试验判决(ML-ITDD)载波同步算法联合导频和迭代译码软信息进行载波估计,粗估计部分仅基于最大似然估计算法进行相位估计,是导致ML-ITDD算法频率估计范围受限的一个因素;首先细估计部分对Turbo译码器迭代输出的软信息进行试验判决,判决后的信息位经过重新编码,联合导频序列映射成调制信号,然后基于最大似然估计算法进行频率细搜索.该方法只能校正较小范围的频偏(ΔfTs≤7×10-4),并且对试验判决后的信息需要重新编码,造成ML-ITDD算法的复杂度很大.另外,非数据辅助M2S2O迭代载波同步算法[8]能校正大范围的载波频偏和相偏,获得接近理想Turbo译码的误比特性能,但必须采用频相二维搜索,运算复杂度非常高,难以在实际系统中应用.因此,针对低信噪比短突发系统,利用尽量短的导频联合译码软信息对较大范围内的频偏进行估计,是目前载波同步的一个研究趋势.
在短突发通信系统中,导频的位置对载波参数的估计范围和估计精度有重要的影响[12-13].为获得较大的载波参数估计范围和较高的估计精度,基于Preamble-Middle(PM)的导频结构并借鉴对Turbo译码软信息进行试验判决的思想,笔者提出了一种新的联合导频和迭代译码的载波同步算法.首先利用去调制的导频序列的所有相关函数对载波参数进行粗估计,用频率和相位的粗估值校正接收信号;然后重新利用导频序列和扩展Turbo译码器输出的信息位和校验位的软信息基于最大似然估计算法进行载波参数的细估计,进而实现有效的载波同步.

图1 联合导频和Turbo迭代译码的载波同步系统模型
1 系统模型
图1给出了联合导频和Turbo迭代译码的载波同步算法的系统模型.数据d首先通过并行Turbo编码器,编码后码字c与导频序列复用,再通过QPSK调制器,调制信号s通过高斯白噪声信道,且附加载波频偏和随机相偏.假设系统的符号定时已经通过导频和数据确定,接收端的基带信号可以表示成

其中,Ts是符号周期;Δf是载波频偏,且满足ΔfTs≪1;φ是相位偏移,建模为Random Walk模型,相偏为均值属于[-π,π]、标准差为σφ的高斯分布;wk是一个复高斯随机变量,均值为零,方差为
在接收端,接收信号首先被送到QPSK解调器和解复用器,提取出导频序列并送至载波估计器进行载波粗估计;用粗估计出的频率和相位对接收信号进行补偿,将补偿后的信号重新送至QPSK解调器和解复用器并提取出信息序列送至Turbo译码器;Turbo译码器输出的软信息和导频序列重新被送到载波同步估计器进行细估计;经过一定次数的迭代译码,最后提取出扩展Turbo译码器输出的信息位软信息并进行硬判决,即恢复出信息比特序列.
2 联合导频和Turbo迭代译码的载波同步算法
2.1 基于导频序列的粗估计
图2给出了以下3种帧结构:导频平均放置在数据段前后的Preamble-Postamble(PP)结构,导频平均分成两段插入到数据中的Preamble-Middle(PM)结构以及导频平均分成几段插入到数据中的Preamble-Middle-Preamble-Middle(PMPM)结构.图中,D是相邻导频之间的距离,L是总的导频长度,N是总的数据长度.

图2 数据帧结构
文献[12]针对PP结构利用了一种相位估计算法,即


文献[3]为提高低信噪比时估计算法的抗噪声能力,对PP结构利用接收导频信号的所有相关函数之和进行频率估计.当导频长度达到120 bit时,该算法联合细估计算法只能校正ΔfTs≤6×10-4范围的归一化频偏;当归一化频偏ΔfTs=2×10-4,误码率为10-4时,相比理想同步条件下信噪比损失在0.5 dB以上.
借鉴文献[3]的思想,利用去调制后的导频序列的所有相关函数之和进行频率估计,即

可以证明归一化频率估计方差为

相应的相位估计可以表示为
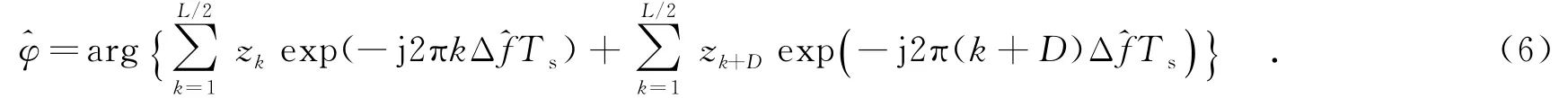
针对图2中的PP和PM数据帧结构,可以分别利用式(4)和式(6)进行频率和相位估计,只是对于不同的导频结构,相邻两段导频的距离D不同.根据归一化频率估计方差和频率估计范围,可以看出针对不同的导频结构,频率偏差的估计范围和估计精度也不同,如PP结构的D最大,它的频率估计精度最高,PM结构的估计精度较高;而PP结构的频率估计范围最小,PM结构的频率估计范围较大.针对多段的PMPM结构,利用相邻两段导频求相关和并累加对频率进行估计,其中,为分段数.分的段数越多,频率的估计范围就越大,同时频率估计精度就越低.
2.2 联合导频和迭代译码的细估计算法
在接收端如果没有理想的载波同步,进入Turbo译码器的信息就会有附加的频偏和相偏,使得进入译码器的先验信息变得不可靠,进而导致译码器不能正确译码.所以进入译码器之前,首先利用导频序列进行载波参数粗估计,保证接收信号的剩余频偏能够使Turbo译码收敛;然后重新利用导频序列和译码器输出信息位和校验位的软信息基于最大似然算法进行载波参数细估计.载波同步原理图如图3所示.
接收序列r={rk,k=0,1,…,K-1},通过载波粗估计并对其进行补偿,将补偿后的信号依次通过解调器、解复用器和扩展Turbo译码器.假定Turbo码的码率为1/3,可以分别得到译码器输出的系统位、第1校验位和第2校验位3路软信息Λd、Λp1和Λp2,再将这3路软信息进行硬判决,硬判决后的信息与导频序列复用;然后将复用后的信号通过调制器,得到调制信号;最后将调制信号和接收信号同时送至最大似然估计器对载波进行细估计,用细估计出的频率和相位重新校正接收信号,校正后的信号用于下一次迭代译码,直至满足一定的迭代次数,迭代即停止.其频率估计和相位估计为

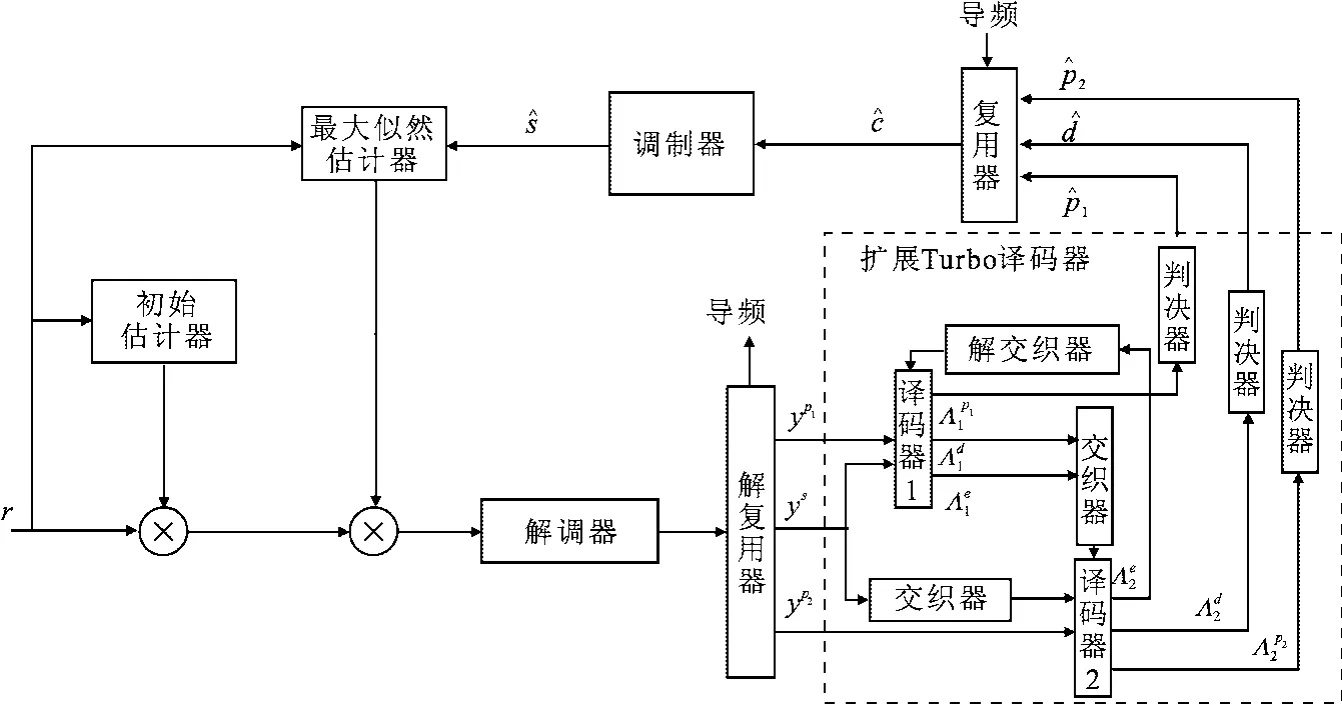
图3 联合导频和Turbo迭代译码的载波同步算法原理框图
3 仿真结果与分析
下面对算法的性能进行分析.仿真参数如下:信息序列长度N=256 bit,码率为1/3,并行Turbo码的递归系统生成多项式g=(5,7)8,进行6次迭代译码.
3.1 粗估计范围及分析
图4分别给出了PP、PM、PMPM这3种导频结构的归一化频率均方根误差曲线及估计范围曲线,其中导频为32个QPSK符号.理论上,根据式(5)和归一化频率估计范围,可以分析出D越大,其频率估计精度越高,同时频率估计范围就会越小.从图4(a)~(c)中可以看出,PP结构具有最高的估计精度,PM结构次之,PMPM结构估计精度最差.在低信噪比范围内,各自频率估计范围内最大归一化剩余频偏分别为ΔfTs=6×10-5,ΔfTs=1.3×10-4,ΔfTs=2.5×10-4.由于PP结构的D最大,即前后导频的距离最远,所以它的估计范围最小.从图4(d)可以看出,PMPM结构的频率估计范围最大,PM结构次之,PP结构估计范围最小,其归一化频偏估计范围依次能达到因此,为了兼顾粗估计具有较大的估计范围和较高的估计精度,笔者选择PM数据帧结构.
3.2 误码率性能及分析
图5给出了归一化频偏ΔfTs分别为0、1.0×10-5、1.0×10-4、2.0×10-4、3.0×10-4时对Turbo码性能的影响.从仿真图中可以看出,当误码率在10-3~10-5范围内时,归一化频偏ΔfTs为1.0×10-5、1.0×10-4、2.0×10-4、3.0×10-4,相比无频偏条件下信噪比依次损失了0.25 dB、0.5 dB、1 dB、2.5 dB,所以针对在低信噪比条件下工作的Turbo码,归一化频偏在ΔfTs<2.0×10-4范围内Turbo译码的误比特性能影响较小.图6给出了当信噪比时,导频长度对使用ML-ISDD算法频率粗估计和使用笔者提出的算法频率粗估计的影响.从图中可以看出,笔者提出的粗估计算法的频率估计精度明显优于最大似然估计算法频率估计精度.当导频为22 bit时,笔者提出的粗估计算法的归一化频偏均方根误差略大于2.0×10-4,而最大似然估计算法的归一化频偏均方根误差达到2.0×10-3.结合图5,当剩余归一化频偏ΔfTs>2.0×10-4时,对Turbo译码的误比特性能影响很大,造成信噪比损失在1 dB以上.当导频达到60 bit时,笔者提出的粗估计算法的归一化频偏均方根误差小于1.2×10-4,并逐渐趋于1.0×10-4,而最大似然估计算法的归一化频偏均方根误差几乎接近5.0×10-4.所以,为保证笔者提出的算法经过粗估计后的剩余归一化频偏ΔfTs<2.0×10-4,Turbo译码能够收敛,同时为使得频率的估计范围较大,采用长度为32个符号的导频,基于PM结构联合导频和Turbo迭代译码软信息进行载波估计并进行性能仿真,且与ML-ISDD算法和ML-ITDD算法进行比较.
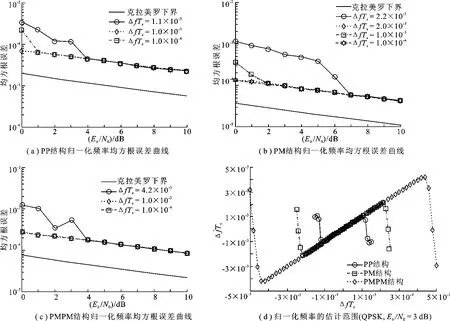
图4 不同导频结构的频率归一化均方根误差曲线和估计范围曲线

图5 频偏对Turbo码性能的影响
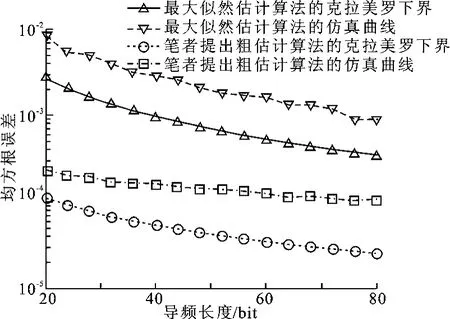
图6 导频长度对最大似然估计算法以及笔者提出的频率粗估计算法的影响

图7 联合导频和迭代译码载波同步算法下的误比特性能
图7给出了笔者提出的算法在归一化频偏ΔfTs为1.5×10-3和1.0×10-4、ML-ISDD算法和MLITDD算法在归一化频偏ΔfTs为9.0×10-4和6.0×10-4时Turbo码的误码率曲线与理想曲线的比较图,其中相偏均采用均值属于[-π,π)、方差为5°的高斯随机变量.从仿真图中可以看出,无论是在小频偏(ΔfTs=1.0×10-4)或是较大频偏(ΔfTs=1.5×10-3)的条件下,笔者提出的算法均能有效地估计并校正载波偏差,获得几乎接近理想同步条件下Turbo译码的误比特性能.在误码率为10-2~10-6时,信噪比损失在0.3 dB以内.而ML-ISDD算法和ML-ITDD算法在其频率估计范围内,如仿真图中归一化频偏为6.0×10-4时,能够校正并获得接近理想的误码率性能;若超出了频率估计范围,如归一化频偏为9.0×10-4时,误码性能严重下降.由于ML-ISDD算法和ML-ITDD算法粗估计采用最大似然估计算法,导频序列很短,导致粗估计的频率估计精度很低,进行粗估计后的剩余频偏很大,使得Turbo译码每次迭代使用的软信息不可靠,进而细估计不能对较大的频偏进行正确的跟踪,导致误比特性能损失很大.
3.3 算法复杂度
笔者所提的算法与ML-ISDD算法和ML-ITDD算法一样需要载波偏移粗估计和细估计两步实现.在粗估计部分,笔者提出的算法利用导频序列去调制信号的所有相关函数进行载波频率估计,与ML-ISDD算法和ML-ITDD算法中基于导频序列的最大似然估计频率搜索相比,基于时域相关的方法较频域频率搜索相比大大降低了运算复杂度;在细估计部分,与ML-ITDD算法相比,笔者提出的算法直接对判决信息进行复用、调制,省去了重新编码的过程,与ML-ISDD算法相比,笔者提出的算法没有对软信息进行非线性变化的过程,因此,在兼顾较大的估计范围和较好的估计性能的前提下,笔者提出的算法的运算复杂度很小,易于在工程中实现.
4 总 结
针对低信噪比、较大频偏条件下短突发通信系统的载波同步问题,笔者首先根据导频提出新的粗估计算法,提高了频率估计精度,并通过设计合适的导频结构来扩大粗估计的频率范围;然后重新利用导频序列和Turbo译码器输出的软信息进行载波细估计.仿真结果表明,笔者提出的算法可以校正较大范围内的频偏,同步范围较大,同时仅需要很短的导频开销,就能使得Turbo译码在剩余频偏范围内的误码率曲线接近理想曲线.与其他方案相比,笔者提出的方案复杂度较低,适合于短突发通信系统.
[1]Mengli U,D’Andrea A N.Synchronization Techniques for Digital Receivers[M].New York:Plenum Press,1997:79-97.
[2] 朱勇刚,姚富强,刘永祥.一种适用于低信噪比的ML载波频偏估计方法[J].系统工程与电子技术,2011,33(2): 427-431. Zhu Yonggang,Yao Fuqiang,Liu Yongxiang.ML-based Carrier Frequency Offset Estimation and Its Low SNR Threshold[J].Systems Engineering and Electronics,2011,33(2):427-431.
[3] 晏辉,唐发建,张忠培.一种基于低码率LDPC码的编码与导频联合辅助载波同步算法[J].电子与信息学报,2011,33(2):470-474. Yan Hui,Tang Fajian,Zhang Zhongpei.A Joint Assisted Carrier Synchronization Algorithm with Code and Pilot Based on Low Rate LDPC Code[J].Journal of Electronics&Information Technology,2011,33(2):470-474.
[4] 史治平,唐发建,晏辉.极低信噪比下的导频联合编码辅助载波同步算法[J].电子与信息学报,2011,33(10):2506-2510. Shi Zhiping,Tang Fajian,Yan Hui.Joint Assisted Carrier Synchronization Algorithm by Pilot and Code at Extremely Low SNR[J].Journal of Electronics&Information Technology,2011,33(10):2506-2510.
[5]包建荣,詹亚峰,陆建华.基于LDPC译码软信息的迭代载波恢复[J].电子与信息学报,2009,31(10):2416-2420. Bao Jianrong,Zhan Yafeng,Lu Jianhua.Iterative Carrier Recovery Based on Soft Decision Metrics of LDPC Decoding [J].Journal of Electronics&Information Technology,2009,31(10):2416-2420.
[6]Rahamim Y,Freedman A,Reichman A.ML Iterative Soft-Decision-Directed(ML-ISDD):a Carrier Synchronization System for Short Packet Turbo Coded Communication[J].IEEE Transactions on Communications,2008,56(7):1169-1177.
[7]Rahamim Y,Freedman A,Reichman A.ML Iterative Tentative-Decision-Directed(ML-ITDD):a Carrier Synchronization System for Short Packet Turbo Coded Communication[C]//11th IEEE Conference on Electronics,Circuits and Systems. Piscataway:IEEE,2004:346-349.
[8]Freedman A,Rahamim Y,Reichman A.Maximum-Mean-Square Soft-Output(M2S2O):a Method for Carrier Synchronization of Short Burst Turbo Coded Signals[J].IEE Proceedings:Communications,2006,153(2):245-255.
[9]Sun Jinhua,Zhu Jili,Wu Xiaojun.A Joint Pilot and Demodulation Soft Information Carrier Synchronization for SOQPSK Signals[C]//IEEE Global Symposium on Millimeter Waves.Washington:IEEE Computer Society,2012:512-516.
[10]王西玲.短突发Turbo编码系统的载波同步研究[D].西安:西安电子科技大学,2012.
[11]D’Andrea A N,Mengali U,Reggiannini R.The Modified Cramer-Rao Bound and Its Application to Synchronization Problems[J].IEEE Transactions on Communications,1994,42(2-4):1391-1399.
[12]Godtmann S,Pollok A,Hadaschik N,el at.On the Influence of Pilot Symbol and Data Positioning on Turbo Synchronization[C]//IEEE 65th Conference on Vehicular Technology.Piscataway:IEEE,2007:1723-1726.
[13]Godtmann S,Hadaschik N,Steinert W,et al.A Concept for Data-Aided Carrier Frequency Estimation at Low Signal-to-Noise Ratio[C]//IEEE International Conference on Communications.Piscataway:IEEE,2008:463-467.
(编辑:郭 华)
Joint pilot and iterative decoding carrier synchronization for the short burst transmission system
SUN Jinhua1,WANG Xuemei1,WU Xiaojun2
(1.State Key Lab.of Integrated Service Networks,Xidian Univ.,Xi’an 710071,China; 2.School of Information Engineering,Chang’an Univ.,Xi’an 710064,China)
Considering the low estimation accuracy and small synchronization range of carrier synchronization algorithms in low signal to noise ratio(SNR)for short burst communication systems,a joint pilot and iterative decoding soft-output carrier synchronization algorithm is proposed.Firstly,the received pilot sequence is extracted and modulation is removed,with the modulation-removed signals made cross-correlated.Then the summation of all the correlation values is used to perform initial carrier parameters estimation.Secondly,the pilot sequence is reused with the soft-output information based on the extended Turbo decoder to obtain fine frequency and phase estimation values.Theoretical analysis and simulation results show that the coarse estimation algorithm can satisfy the requirements of the frequency estimation range and estimation accuracy,and preamble-middle pilot placement is optimal for a certain length of the data frame;The turbo decoder can obtain more reliable soft-output information with small residual frequency offset after initial coarse synchronization when the normalized frequency offset is less than 1.5×10-3,with the joint pilot and soft-output of the decoder used to estimate fine carrier parameters,which can make the turbo code achieve optimal BER performance.
synchronization;pilot;Turbo code;soft-output
TN911.23
A
1001-2400(2014)01-0023-06
10.3969/j.issn.1001-2400.2014.01.005
2012-10-18 < class="emphasis_bold">网络出版时间:
时间:2013-09-16
国家自然科学基金资助项目(60902039,61271175);中央高校基本科研业务费专项资金资助项目(K50511010014,K5051201043,CHD2011JC088);长安大学基础研究支持计划资助项目
孙锦华(1979-),女,副教授,博士,E-mail:jhsun@xidian.edu.cn.
http://www.cnki.net/kcms/detail/61.1076.TN.20130916.0926.201401.29_001.html

