一种针对目标跟踪的自适应波形选择方法

靳 标,纠 博,刘宏伟,苏 涛

(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)

一种针对目标跟踪的自适应波形选择方法

靳 标,纠 博,刘宏伟,苏 涛

(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)

在自适应交互多模型的框架下,提出了一种雷达发射波形选择方法.将常速模型和“当前”统计模型应用到交互多模型算法中,得到自适应交互多模型跟踪算法.从信息论的角度出发,对误差椭圆正交法进行了推导,并给出其控制论角度的等价形式.根据这种等价形式,该方法存在无法调节距离和速度跟踪误差权重的问题.针对这个问题,结合自适应交互多模型跟踪算法,提出了基于最小均方误差准则的自适应雷达发射波形选择方法.

认知跟踪;自适应跟踪;交互多模型;波形选择;模糊函数;分数阶傅里叶变换

认知雷达(Cognitive Radar,CR)[1]改变了传统自适应雷达单向的信息处理方式,实现了从接收到发射的闭环处理.它可以通过对外部环境和目标不断的感知,在一定的约束下自适应地选择工作模式、发射波形和接收信号处理方法,充分利用各种信息进行智能化处理,并在日益复杂的环境下最大限度地发挥各种资源的效能.因此,认知雷达一经提出便得到了广泛的关注,并被认为是雷达未来发展的一个重要方向.与此同时,认知雷达这一概念的出现也赋予了发射波形优化新的内涵,如何根据环境和目标的先验信息进行发射端的自适应调整成为波形优化研究的一个热点[2-3].

近年来,针对目标跟踪的发射波形优化受到了广泛的关注[4-8].文献[4]首次在传统的雷达目标跟踪系统中增加了波形自适应选择模块,基于卡尔曼滤波并面向单目标背景,利用参数估计理论中Fisher信息矩阵的逆作为观测噪声协方差,建立了发射波形与跟踪滤波之间的联系,通过波形选择及参数寻优使得跟踪误差达到最小.文献[5-6]利用文献[4]的观测模型,即发射波形估计目标距离和速度的克拉美罗下界(Cramer-Rao Lower Bound,CRLB),分别研究了基于粒子滤波和容积卡尔曼滤波(Cubature Kalman Filter,CKF)等非线性跟踪算法的波形自适应问题,但是二者在波形选择和参数寻优时的复杂度较高,计算量较大.文献[7]讨论了一系列基于目标跟踪的波形选择标准,特别讨论了线性调频(Linear Frequency Modulation,LFM)信号的调频率与目标机动指数[9]的关系,指出最优调频率可以使观测误差椭圆与预测误差椭圆相互正交.这是误差椭圆正交法的雏形,直观地解释了跟踪误差最小所需满足的条件,但是缺乏详细的理论推导.文献[8]将文献[7]的误差椭圆正交理论进行了推广,提出利用分数阶傅里叶变换(Fractional Fourier Transform,Fr FT)来旋转模糊函数,从而完成观测误差椭圆与预测误差椭圆正交,并在交互多模型(Interacting Multiple Model,IMM)框架下使用此方法进行波形选择,最后验证了该方法在目标加速度和状态转移概率信息不准确的情况下的鲁棒性.误差椭圆正交法具有明确的物理意义,而且计算简单,易于求解.但是文献[7-8]只给出了此方法的实验性结果,并未给出其相关的数学推导,而且该方法还存在一个问题,即距离误差和速度误差在量纲上不一致,需要对二者的权重进行调节.此方法的代价函数并未体现,可能造成实际应用时的不便.

为了提高雷达系统的跟踪性能,需要将发射波形选择与自适应的跟踪算法相结合.传统的针对目标跟踪的波形选择方法都是在非自适应跟踪算法的基础上进行的[4-8].笔者将认知雷达的概念应用于跟踪系统,提出在自适应跟踪算法的基础上进行波形优化,可以大幅度地提高雷达系统的跟踪性能.首先将常速(Constant Velocity,CV)模型和“当前”统计模型应用到交互多模型算法中,得到自适应交互多模型(Adaptive Interacting Multiple Model,AIMM)算法.在此基础上,从信息论的角度推导了误差椭圆正交法,并给出了其控制论角度的等价形式.然后针对此波形选择方法存在的无法调节距离和速度跟踪误差权重的问题,基于最小均方误差准则提出了相应的解决方法.

1 基于自适应交互多模型的目标跟踪数学模型

目标的运动模型可以分为非机动目标运动模型和机动目标运动模型.文中非机动目标运动模型采用标准的常速模型[10],机动目标运动模型采用“当前”统计模型[11].将这两个模型应用于交互多模型[12]框架,便得到了自适应交互多模型算法.在自适应交互多模型算法中,动态噪声方差是自适应变化的,这是与传统交互多模型算法的最大区别.这种两模型的交互多模型,一方面由于模型个数少,可以减少跟踪算法的运算量;另一方面由于动态噪声方差的自适应变化,可以提高系统的跟踪性能.

1.1 动态模型

目标的动态方程为

其中,i=1,表示非机动目标运动模型;i=2,表示机动目标运动模型.F为状态转移矩阵,U为加速度输入矩阵,w为动态噪声,为加速度均值.

1.2 观测模型

目标的观测方程为

式中,H为观测矩阵,v为观测噪声.

传统的雷达只使用距离的观测数据进行跟踪.文献[13]指出引入速度观测之后,会明显提高雷达的跟踪性能.笔者所考虑的是距离和速度共同观测的情况,故观测矩阵观测噪声vk与xk|k-1独立,且vk～N(0,Rk),其中Rk为观测噪声的协方差,令其等于k时刻发射波形估计目标距离和速度的克拉美罗下界,即考虑完全检测的情况[4].这样就建立起了跟踪系统与发射波形之间的关系.图1给出了观测噪声的协方差Rk与发射波形的关系.图1中,f0(t)为基础波形,即单频信号;A0(τ,υ)为f0(t)对应的模糊函数,是关于时延τ和多普勒频移υ的二维函数;J0为f0(t)对时延τ和多普勒频移υ估计的Fisher信息,可表示为在原点处的海森矩阵[14];η为雷达系统的信噪比;R0为基础波形f0(t)对目标的距离和速度估计的克拉美罗下界[14];T为[τ,υ]T到[r,̇r]T的变换矩阵,即

其中,c为光速,fc为雷达载频.

图1 观测噪声的协方差与发射波形的关系

如图1所示,对模糊函数A0(τ,υ)在时延-多普勒平面进行角度为φk的旋转,对应的发射波形f0(t)要进行分数阶因子为的分数阶傅里叶变换[15].由于文中的讨论不需要涉及分数阶傅里叶变换的具体算法,所以在此不再赘述.根据图1所示的思路,可得k时刻的发射波形fk(t)所对应的估计目标距离和速度的克拉美罗下界为

其中,R0为基础波形f0(t)估计目标的距离和速度的克拉美罗下界;旋转矩阵φk为k时刻模糊函数A0(τ,υ)在时延-多普勒平面的旋转角度,φk对应的发射波形为fk(t),即对基础波形f0(t)进行分数阶因子为的分数阶傅里叶变换.

2 基于自适应交互多模型的发射波形选择方法

2.1 误差椭圆正交法

大多数针对目标跟踪的波形选择方法都是对波形的时宽、调频率等参数进行直接寻优[4-7],从而找到使跟踪误差最小的发射波形.文献[8]提出利用分数阶傅里叶变换来旋转模糊函数,使得观测误差椭圆与预测误差椭圆相互正交,从而使跟踪误差最小.这样误差椭圆正交法把原来对波形的各个参数进行寻优的多变量优化问题转化成只优化模糊函数的旋转角度的单变量问题,降低了运算复杂度,而且该方法具有直观的物理意义.如图2所示,图2(a)和图2(b)是两个误差椭圆不正交的情况;图2(c)是两个误差椭圆正交的情况.显然,当两椭圆正交时,重叠区域的面积最小,即跟踪误差最小.但是文献[8]只给出了此方法的实验性结果,并没有给出相关的数学推导.笔者从最大互信息的角度对此方法加以推导,并给出其在控制论角度的等价形式.

图2 误差椭圆相交的不同情况

将卡尔曼滤波的观测方程式(2)代入式(5),可得目标状态预测值xk|k-1与观测值zk的互信息

其中,I为单位矩阵,Rk(φk)由式(4)给出,Pk|k-1为自适应交互多模型框架下预测误差的协方差,即

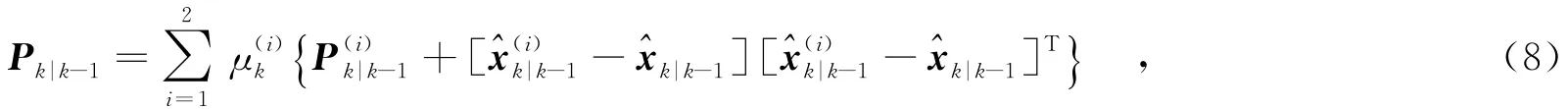
由式(6)可得目标状态预测值xk|k-1与观测值zk的互信息为

由卡尔曼滤波算法可得后验估计误差协方差Pk|k的行列式为

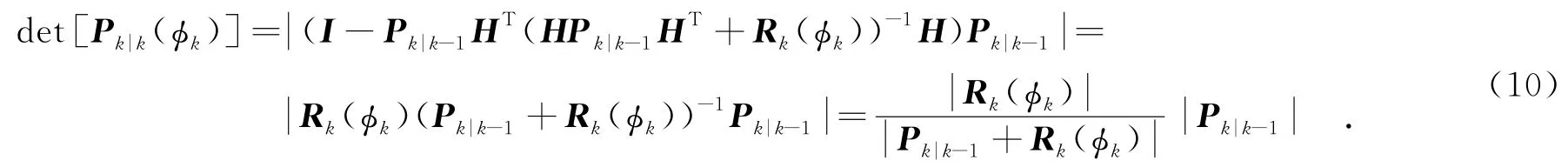
由于Pk|k-1与波形参数φk无关,故等价,即等价.所以,误差椭圆正交法在控制论角度的等价形式是

即后验估计误差协方差Pk|k的行列式最小.

2.2 最小跟踪误差法

误差椭圆正交法物理意义明确,而且容易求解.但是,此方法存在一个问题,即距离误差和速度误差在量纲上不一致,需要利用一个调节因子对二者的权重进行调节,而此方法的代价函数式(11)并未体现,这有可能造成实际应用时的不便.针对此问题,笔者从最小跟踪误差的角度提出了相应的解决方法.

文献[4]提出了一种基于跟踪误差最小的代价函数:

即后验估计误差协方差Pk|k的迹最小.但是此代价函数仍未考虑距离跟踪误差与速度跟踪误差在量纲上不一致的问题.针对这个问题,文献[5-6]中的代价函数均有体现,即在式(12)中加入一权重因子γ,对距离跟踪误差和速度跟踪误差进行调节

其中,p11为Pk|k的第1行第1列的元素,代表距离跟踪误差方差;p22为Pk|k的第2行第2列的元素,代表速度跟踪误差方差;Γ=diag{1,γ},γ的单位为s2.当γ=1 s2时,式(13)与式(12)相同.

式(13)中的权重因子γ可以调节距离跟踪误差和速度跟踪误差的权重,但是在实际应用中,权重因子γ的值并不好确定.笔者提出一种实际应用中更容易操作的代价函数:

其中,ξ为速度跟踪精度需满足的门限,即在速度跟踪满足一定精度要求的条件下,寻找令距离跟踪误差最小的发射波形.

3 仿真结果及分析

首先通过仿真说明代价函数式(13)和式(14)对距离跟踪误差和速度跟踪误差的调节作用,其次将说明在自适应交互多模型框架下进行发射波形选择的优势,对比算法为文献[8]中的方法.为了突出波形选择的效果,还添加了在标准交互多模型和自适应交互多模型框架下,不含波形选择的跟踪结果.

仿真场景考虑一分段机动运动目标,跟踪参量为目标的径向距离和径向速度.假定目标的初始距离和速度目标在总观测时间100 s内经历了5个不同的运动状态,分别对应5个不同的平均加速度,每个运动状态的持续时间为20 s.跟踪器的状态转移概率矩阵为

矩阵MTracker中第i行第j列元素表示状态i到状态j的转移概率.其他参数为:观测间隔Δt=1 s,基础波形f0(t)的时宽T0=10μs,雷达系统的信噪比为16 dB,载频fc=10.4 GHz.仿真结果由100次蒙特卡洛实验统计得到.

图3为在标准交互多模型框架下,分别利用误差椭圆正交法(IMM-WS1,即文献[8]的方法)、式(13)(其中γ=0.3 s2)(IMM-WS2)和式(14)(其中ξ=(14.2 m/s)2)(IMM-WS3)作为代价函数的距离跟踪均方根误差和速度跟踪均方根误差.从图3中可以看出,利用式(13)和式(14)作为代价函数可以灵活地调节距离跟踪误差和速度跟踪误差的权重,这样可以避免因为距离误差和速度误差在量纲上的不一致而带来的工程应用上的不便.但是,距离跟踪精度和速度跟踪精度本身是一对矛盾,它们此消彼长,距离跟踪精度的提高是以速度跟踪精度的损失为代价的,反之亦然.在实际情况中,需要结合目标的运动状态和工程需要对式(13)和式(14)中的调节参数进行预先设定.显然,式(14)在满足速度跟踪精度的要求下,令距离跟踪误差最小,在实际应用中更容易操作.

图4分别为在标准交互多模型和自适应交互多模型的框架下,不含波形选择的方法(IMM-WS0/ AIMM-WS0)、利用误差椭圆正交法(IMM-WS1,即文献[8]的方法/AIMM-WS1)及利用式(12)作为代价函数方法(IMM-WS2/AIMM-WS2)的距离跟踪均方根误差、速度跟踪均方根误差和模糊函数的旋转角度.从图4(a)和(b)中可以看出,含波形选择方法的跟踪性能要好于不含波形选择的方法,这说明通过发射波形的自适应选择可以提高雷达系统的跟踪精度.另外,误差椭圆正交法的跟踪性能与利用式(12)作为代价函数的方法性能非常接近,这是由于其代价函数式(11)与式(12)数学形式接近,对距离和速度的估计性能是相当的.更重要的一点是,基于自适应交互多模型的波形选择方法明显优于基于标准交互多模型的波形选择方法.在图4(c)中,标准交互多模型框架下利用误差椭圆正交法(IMM-WS1,即文献[8]的方法)及利用式(12)作为代价函数(IMM-WS2)的方法,对模糊函数的旋转角度大约在104.2°,而在自适应交互多模型框架下利用误差椭圆正交法(AIMM-WS1)及利用式(12)作为代价函数(AIMM-WS2)的方法,对模糊函数的旋转角度大约在102.3°.这说明在自适应交互多模型框架下,利用较小的模糊函数旋转角度就可以达到距离和速度的跟踪精度要求,而在标准的交互多模型框架下,要满足给定的跟踪精度则需要对波形进行更大的自适应变化.所以在自适应交互多模型框架下进行发射波形优化更具优势,正是跟踪算法与发射波形共同的自适应调整使得最终的跟踪误差达到最小.

图3 标准交互多模型框架下不同波形选择方法的仿真结果

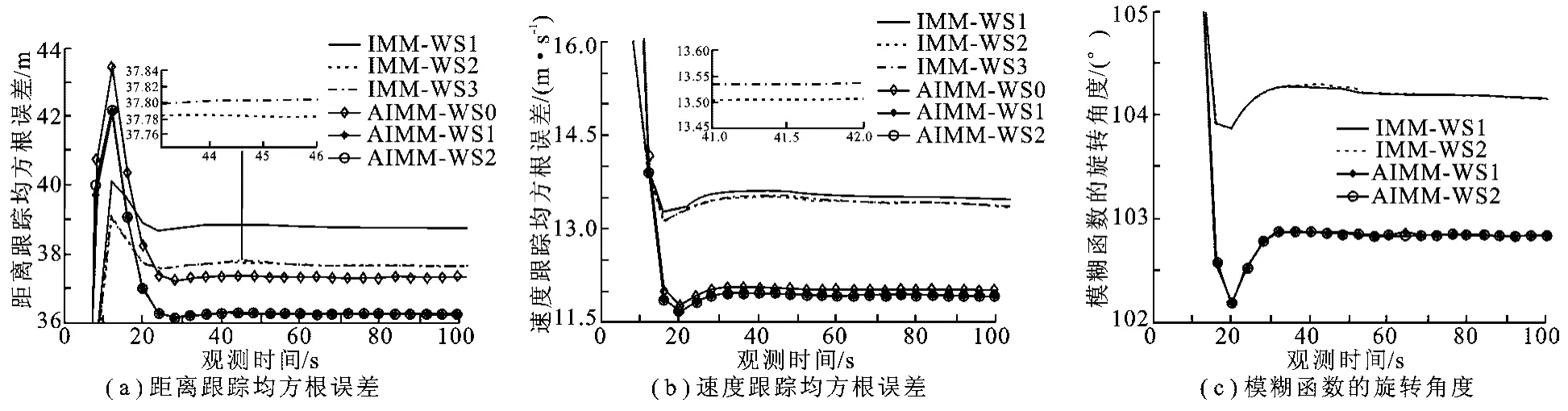
图4 不同模型下各种波形选择方法的仿真结果

4 总 结

笔者首先将常速模型和“当前”统计模型加入交互多模型方法,得到自适应交互多模型跟踪算法,并结合该算法,提出了基于最小均方误差准则的自适应发射波形选择方法.仿真结果表明:笔者提出的算法解决了误差椭圆正交法不能调节距离和速度跟踪误差权重的问题,而且在自适应交互多模型跟踪算法的基础上进行发射波形选择,可以显著地提高系统的跟踪性能.但在实际中,雷达发射机通常工作在饱和状态下,很难实现对发射信号的幅度调制.因此,如何在发射信号的恒模约束下进行自适应发射波形优化设计将是进一步研究的重点.

[1]Haykin S.Cognitive Radar[J].IEEE Signal Processing Magazine,2006,23(1):30-40.

[2]Cochran D,Suvorova S,Howard S D,et al.Waveform Libraries[J].IEEE Signal Processing Magazine,2009,26(1): 12-21.

[3]Sira S P,Li Ying,Papandreou-Suppappola A,et al.Waveform-agile Sensing for Tracking[J].IEEE Signal Processing Magazine,2009,26(1):53-64.

[4]Kershaw D J,Evans R J.Optimal Waveform Selection for Tracking Systems[J].IEEE Transactions on Information Theory,1994,40(5):1536-1550.

[5]Sira S P,Papandreou-Suppappola A,Morrell D.Dynamic Configuration of Time-varying Waveforms for Agile Sensing and Tracking in Clutter[J].IEEE Transactions on Signal Processing,2007,55(7):3207-3217.

[6]Haykin S,Zia A,Arasaratnam I,et al.Cognitive Tracking Radar[C]//Proceedings of the IEEE Radar Conference. Washington:IEEE,2010:1467-1470.

[7]Niu R X,Willett P,Bar-Shalom Y.Tracking Considerations in Selection of Radar Waveform for Range and Range-Rate Measurement[J].IEEE Transactions on Aerospace and Electronic Systems,2002,38(2):467-487.

[8]Savage C O,Moran B.Waveform Selection for Maneuvering Targets within an IMM Framework[J].IEEE Transactions on Aerospace and Electronic Systems,2007,43(3):1205-1214.

[9]Bar-Shalom Y,Li X R,Kirubarajau T.Estimation with Application to Tracking Navigation[M].New York:Wiley,2001:280-281.

[10]Li X R,Jilkov V P.Survey of Maneuvering Target Tracking.Part I:Dynamic Models[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(4):1333-1364.

[11]周宏仁,敬忠良,王培德.机动目标跟踪[M].北京:国防工业出版社,1991:10-20.

[12]Blom H A P,Bar-Shalom Y.The Interacting Multiple Model Algorithm for Systems with Markovian Switch Coefficients [J].IEEE Transactions on Automatic Control,1988,33(8):780-783.

[13]张怀根,张林让,吴顺君.利用径向速度观测值提高目标跟踪性能[J].西安电子科技大学学报,2005,32(5):667-670. Zhang Huaigen,Zhang Linrang,Wu Shunjun.The Use of the Radial Velocity to Improve the Performance of Target Tracking[J].Journal of Xidian University,2005,32(5):667-670.

[14]Van Trees H L.Detection,Estimation,and Modulation Theory:PartⅢ[M].New York:Wiely,2001:275-308.

[15]Stankovic'L,Djurovic'I.Relationship Between the Ambiguity Function Coordinate Transformations and the Fractional Fourier Transform[J].Annales des Telecommunications,1998,53(3/4):91-94.

[16]Williams J L.Information Theoretic Sensor Management[D].Massachusetts:Massachusetts Institute of Technology,2007.

[17]Suvorova S,Howard S D,Moram W,et al.Waveform Libraries for Radar Tracking Applications[C]//Proceedings of IEEE Conference on Infromation Science and Systems.Piscataway:IEEE,2007:1424-1428.

(编辑:郭 华)

Adaptive waveform selection approach for target tracking

JIN Biao,JIU Bo,LIU Hongwei,SU Tao
(National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China)

Within an adaptive interacting multiple model(IMM)framework,an approach to selecting the transmitted waveform of radar is proposed.The adaptive IMM algorithm is attained when the constantvelocity(CV)model and the current statistical model are applied to the IMM filter.Firstly,the error ellipse orthogonal method is derived from information theory,and an equivalent form is given in terms of control theory.According to the equivalent form,the range and velocity tracking error can not be adjusted effectively using the error ellipse orthogonal method.To solve this problem,an adaptive transmitted waveform selection approach is proposed based on the minimum mean-squared error,combining with the adaptive IMM algorithm.Simulations show that the proposed algorithm is feasible and effective.

cognitive tracking;adaptive tracking;interacting multiple model;waveform selection; ambiguity function;fractional Fourier transform

TN953

A

1001-2400(2014)01-0057-07

10.3969/j.issn.1001-2400.2014.01.011

2012-11-07 < class="emphasis_bold">网络出版时间:

时间:2013-09-16

国家自然科学基金资助项目(61271291,61201285);新世纪优秀人才支持计划资助项目(NCET-09-0630);国家自然科学基金青年科学基金资助项目(61001204)

靳 标(1986-),男,西安电子科技大学博士研究生,E-mail:jinpuresky@hotmail.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20130916.0926.201401.73_007.html