基于改进PSO-BP神经网络的变压器故障诊断
张国祥,袁丹,张浩,彭道刚
(1.上海电力学院自动化工程学院,上海200090; 2.国网浙江宁波市鄞州区供电公司,浙江宁波 315100)
变压器作为电力系统的重要设备,其运行的可靠性直接影响整个电力系统的安全性和经济性.在现有的变压器故障诊断方法中,油中溶解气体分析技术为常用手段之一,但由于变压器发生故障时与多种因素存在耦合,很难通过理论分析获得油中特征气体浓度到变压器故障类型的映射.多层前馈神经网络具有很强的非线性映射能力,非常适合特征气体浓度到变压器故障类型的映射,因此它在变压器故障诊断中得到了广泛应用.
误差反向传播(Error Back Propagation)算法及其改进算法可以有效提高训练的收敛速度.[1-2]由于误差曲线的复杂性,随机选择的初始值往往在局部极小点附近,需要增加网络规模才能满足训练结果,这导致训练后的网络泛化能力下降.采用粒子群算法来获得网络的初始权值和阈值可以提高其收敛性能.[2-3]
1 BP神经网络算法
BP神经网络是一种多层前馈神经网络,其主要特点是信号前向传递,误差反向传播.每一层的神经元状态只影响下一层神经元状态,如果前向传播输出与期望输出的误差达不到预期的精度,则会沿着误差的负梯度方向来调整各层神经元的权值和阈值.如此反复,直至网络误差达到预期精度.[1-2]由此可知,BP神经网络是基于梯度下降法的,不考虑以前的经验积累,学习过程收敛缓慢,易陷入局部极小值.对于这一问题,本文采用附加动量方法加以解决.带附加动量的权值学习公式为:
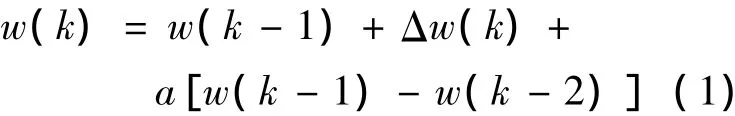
式中:w(k),w(k-1),w(k-2)——k,k-1,k-2时刻的权值;
a——动量学习率.
2 PSO算法及其改进
2.1 标准粒子群算法
粒子群算法中每个粒子都代表问题的一个潜在解,每个粒子对应一个由适应度函数决定的适应度值,粒子的速度决定了粒子移动的方向和距离,速度随自身及其他粒子的移动经验进行动态调整,从而实现在可解空间中的寻优.[2-4].
标准粒子群算法的极值寻优算法流程如图1所示.
假设在一个D维的搜索空间中,由n个粒子组成的种群为X=(X1,X2,X3,…,Xn),其中第i个粒子表示一个D维的向量Xi=(xi1,xi2,xi3,…,xiD)T,代表第i个粒子在D维搜索空间中的位置,也代表问题的一个潜在解.根据目标函数即可计算出每个粒子Xi对应的适应度值.在每一次迭代过程中,粒子通过个体极值和群体极值更新自身的速度和位置.
粒子速度和位置的更新公式为:

式中,Vid——第i个粒子的速度;
Xid——第i个粒子的位置;
Pid——个体极值;
Pgd——群体极值;
w——惯性权重;
k——当前迭代次数;
c1,c2——加速度因子,是非负的常数;
r1,r2——分布于[0,1]之间的随机数.
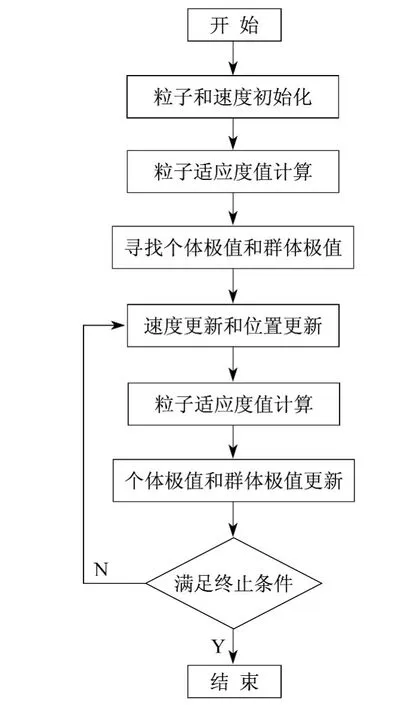
图1 PSO算法流程
2.2 引入动态变异的改进粒子群算法
虽然粒子群优化算法收敛快,具有很强的通用性,但同时也存在着容易早熟收敛、收敛精度较低、后期迭代效率不高等缺点.[4]因为在迭代过程中,所有粒子都向最佳位置逼近.如果该位置是一局部最佳位置,粒子群就无法在解空间内重新进行搜索,从而陷入局部最优解,而无法找到全局最优解.
在PSO算法中引入变异操作,即对某些粒子以一定的概率重新初始化.变异操作拓展了在迭代过程中不断缩小的种群搜索空间,使得粒子能够跳出先前搜索到的最优位置,在更大空间中展开搜索,同时又保持了种群的多样性,提高了算法找到全局最优值的可能性.
本文引入线性动态变异算子,即:

式中:P(n)——当前变异概率;
n——当前迭代次数;
N——最大迭代次数;
Pmax,Pmin——最大变异概率和最小变异概率.
刚开始迭代时,种群以一个极小的概率发生变异,几乎不发生变异,至迭代后期,变异概率迅速扩大,粒子可以迅速跳出当前搜索区域,在更大的区域内寻找最优解.
3 改进粒子群算法优化神经网络及网络模型
3.1 改进粒子群算法优化神经网络
改进粒子群算法优化神经网络分为神经网络结构确定、粒子群算法优化和神经网络预测3部分.首先,根据待解决问题的输入参数个数和输出参数个数确定神经网络的拓扑结构,进而可以根据阈值和权值的个数确定粒子群的个体长度.然后,利用粒子群算法优化神经网络的权值和阈值,其中每个粒子个体都包含了一个网络所有的权值和阈值,个体通过适应度函数计算个体适应度值,粒子群算法通过迭代搜索最优适应度值对应的个体.最后,粒子群算法将找到的最优个体赋值给神经网络,使神经网络获得初始权值和阈值,网络经过训练后,预测输出.算法流程如图2所示.
适应度函数选取网络训练后预测输出和期望输出之间的误差绝对值之和,其计算公式为:

式中:yi——网络预测输出;
Yi——网络期望输出;
n——测试样本总数;
k——常数系数.

图2 混合算法流程
3.2 网络模型
相关统计资料表明,放电性故障和过热性故障是变压器故障的主要类型.油中气体的成份、产气速率和含量可以很好地反应这两大类故障.[5-6]
为防止神经网络输入参数过多而导致饱和,本文利用变压器油中H2,CH4,C2H6,C2H4,C2H2共5种气体数据,以它们之间的比值(C2H2/ C2H4,CH4/H2,C2H4/C2H6)作为故障特征量,其中以3个比值作为神经网络的输入向量.采用无故障、中低温过热、高温过热、局部放电、低能量放电、高能量放电6种故障类型作为神经网络的输出向量.当变压器出现某种故障类型时,该对应的故障类型期望输出为1,而其他类型的期望输出为0.
4 实例分析
本文搜集的各类故障情况数据及正常运行数据共计163组,[5,7-9],其中无故障22组,占13.50%;中低温过热40组,占24.54%;高温过热46组,占28.22%;局部放电10组,占6.13%;低能量放电5组,占3.07%;高能量放电40组,占24.54%.[7-9]
为保证网络的可靠性和通用性,将不同故障状况的数据分别随机打乱后重新排序,按比例取其中前100组数据作为训练数据,余下63组数据作为测试数据.
在构建神经网络时,隐含层节点数的选择至关重要,如果隐含层节点数太少,神经网络难以建立复杂的映射关系,网络预测误差较大;如果隐含层节点数过多,网络学习时间增加,可能会出现“过拟合”现象[2,5,9].隐含层节点数分别取1至46,获得46组网络预测误差数据,其中,当隐含层节点数为4,5,29,31,35,36时,网络预测误差相对最小.部分隐含层节点数对应的网络误差如表1所示.考虑到样本数目为100组及逼近映射的复杂程度,本文神经网络隐含层神经元确定为35个.
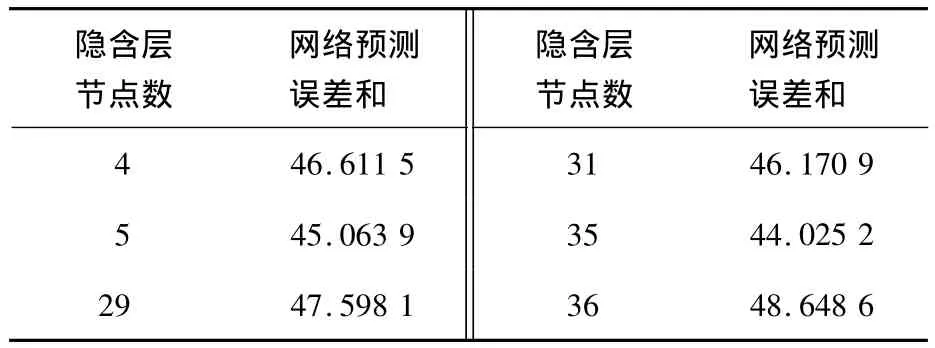
表1 部分隐含层节点数神经网络预测误差
神经网络选用3-35-6的结构.综合考虑种群个体的长度、寻找全局最优解的速度和运行所需时间,确定种群规模为30,最大迭代次数为300;迭代初期种群基本不发生变异,而迭代后期种群将以较大的变异概率来保证种群的多样性,同时为了保留每一代的最优个体,变异概率不应过大,综合考虑,最大变异概率和最小变异概率分别取为0.35和0.01.
根据确定的神经网络结构,分别采用相同层次网络结构的BP神经网络、PSO-BP神经网络、改进PSO-BP神经网络进行学习训练,预测输出.
3 种网络结构的训练误差如图3所示.3种网络结构的训练误差对比如图4所示.
由图3和图4可以看出,无优化的BP网络训练误差明显大于优化后的BP网络,而与标准粒子群优化的BP网络相比,改进的粒子群优化BP网络可以以较少的代数得到充分训练,同时也具有更小的训练误差,由此说明本方法是可行的.
3 种算法的诊断结果如表2所示.对于每一类具体的故障类型,改进PSO-BP算法诊断结果如表3所示.
从表2可以看出,与传统BP算法和PSO优化BP网络算法相比,本文所采用的改进PSO-BP算法具有更高的准确率.
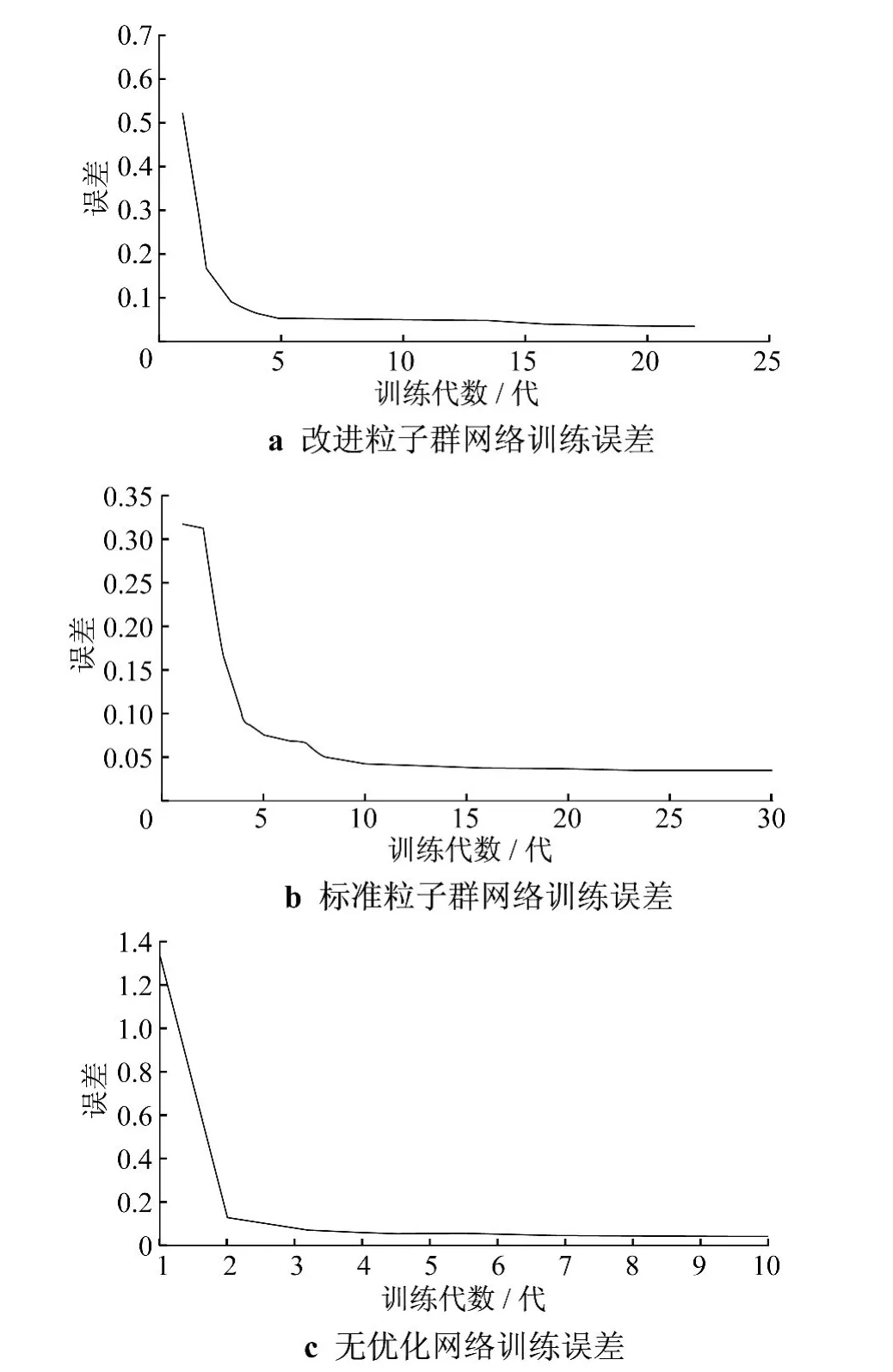
图3 3种网络结构的训练误差
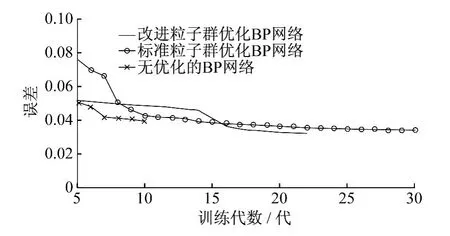
图4 3种网络结构的训练误差对比
从表3可以看出,由于之前网络训练时局部放电和无故障类型的训练数据较少,没有建立良好的映射关系,导致这两类故障类型的正确率不高.而对于局部放电,虽然用于网络训练的数据同样很少,但诊断结果正确,其原因是用于测试该类故障的样本数据与之前该类故障的测试数据较接近.
选取3个典型故障样本数据如表4所示,改进PSO优化BP网络的预测输出结果如表5所示.

表2 不同算法的诊断结果%

表3 改进PSO-BP算法的诊断结果

表4 变压器油中溶解气体体积分数的比值(10e-6)
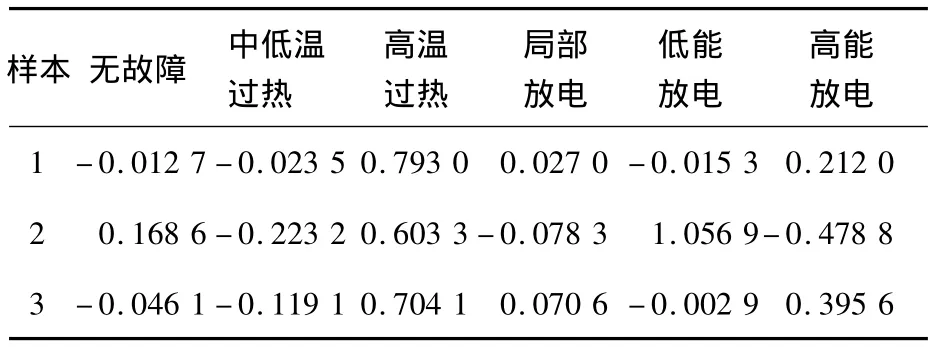
表5 改进PSO优化BP网络的预测输出结果
3 个典型样本用三比值法判断为高温过热、低能放电和高温过热,这与预测输出结果相同.
5 结语
将动态变异引入标准粒子群算法来优化神经网络,该改进算法可以有效避免标准粒子群优化神经网络算法易陷入局部极小值的缺陷,同时又可以有效提高算法的计算精度、收敛速度及网络的稳定性.该改进算法提高了变压器故障诊断的准确率,具有较好的推广应用价值.
[1]高骏,何俊佳.量子遗传神经网络在变压器油中溶解气体分析中的应用[J].中国电机工程学报,2010,30(30): 121-127.
[2]史疯,王小川,郁磊,等.MATLAB神经网络30个案例分析[M].北京:北京航空航天大学出版社,2010:236-242.
[3]程加堂,熊伟,徐绍坤,等.基于改进粒子群优化神经网络的电力变压器故障诊断[J].高压电器,2012,48(2): 42-45.
[4]魏星,舒乃秋,崔鹏程,等.基于改进PSO-BP神经网络和D-S证据理论的大型变压器故障综合诊断[J].电力系统自动化,2006,30(7):46-50.
[5]段侯峰.基于遗传算法优化BP神经网络的变压器故障诊断[D].北京:北京交通大学,2008.
[6]程加堂,熊伟.灰色神经网络在变压器故障诊断中的应用[J].高压电器,2010,46(8):56-58.
[7]王少芳,蔡金锭,刘庆珍.基于改进GA-BP混合算法的电力变压器故障诊断[J].电网技术,2004,28(4):30-33.
[8]王少芳,蔡金锭.GA-BP混合算法在变压器色谱诊断法中的应用[J].高电压技术,2003,29(7):3-6.
[9]刘宁.基于DGA的量子神经网络在变压器状态检修中的应用研究[D].吉林:东北电力大学,2010.
(编辑胡小萍)

