振动筛包覆层大梁低频涡流检测方法研究＊

许晓东 付 胜 吴广明

（1.北京工业大学机械工程与应用电子技术学院，北京市朝阳区，100022；2.大同煤矿集团精煤分公司，山西省大同市，037000）

振动筛是矿山洗选生产的关键设备之一，其安全可靠地运行对整个生产过程具有直接和极其重要的影响。在现代化原煤洗选系统中，各种关键设备层叠安装，振动筛处在中间处理环节，拆卸极为不便，同时振动筛为箱式结构，大梁位于振动筛的筛箱内，两边铆接固定在筛帮上，上面有筛板，下部为漏煤仓，检测空间相当狭小。振动筛的大梁在振动筛中间起着连接和支撑的作用，其受力相当复杂，除了承受设备本身的重力与静作用力外，还要承受动应力与交变应力的作用，因此极易出现疲劳裂纹。另外，为了减少大梁遭受恶劣工作环境条件的侵蚀，在大梁的外壁处覆盖有一层厚度约为7mm的防腐包覆层，如此厚的包覆层使得大梁的检测异常困难。相关专家曾提出运用磁记忆与涡流检测的方法来解决这一问题，但针对振动筛大梁的裂纹此类方法的研究尚不够深入，并没有解决磁记忆的定量与涡流透过包覆层检测定量的问题，而低频涡流检测技术受集肤效应的影响相对较小，检测深度可以大大增加，因此可将低频涡流检测技术运用到具有包覆层的振动筛大梁裂纹检测中，并且可以解决检测参数的选择和实现检测的定性与定量问题。

1 低频涡流检测分析

根据电磁感应原理，当载有交变电流的检测线圈靠近导电试件时，由于线圈中的交变电流产生交变磁场，从而在试件中感生出涡流，涡流产生原理见图1。

图1 涡流产生原理

由图1可见，由于涡流的大小、相位及流动形式受到试件导电性能等的影响，而涡流的反作用磁场又使得检测线圈的阻抗发生变化，因此通过测定检测线圈阻抗的变化，可以得出被检测试件的导电性差别及有无缺陷等方面的结论。

当交变电流通过导线时，导线周围变化的磁场也会在导体中产生感应电流，从而使沿导体截面的电流分布不均匀，表面的电流密度较大，越往中心处就越小，并且按照负指数规律衰减。定义涡流密度衰减到其表面值1／e时的透入深度为标准透入深度，涡流标准透入深度δ为：

式中：f——交流电流频率，Hz；

μ——材料磁导率，H／m；

σ——材料电导率，s／m。针对半无限平面导体，由麦克斯韦电磁场理论，可推导得出距离导体表面x 深度处的涡流密度见式 （2）：

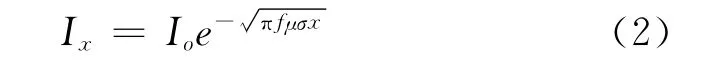
式中：Ix——至表面x 深处的涡流密度，A；

I0——无限大导体半表面的涡流密度，A；

x——至表面的距离，m。

由式（1）和式（2）可知，检测频率对于涡流检测是至关重要的，尽管不能无限制降低频率，但对于某一特定的金属构件检测对象，材料常数都是一个定值，因此可以通过调节频率参数f，使其能够透过一定厚度的包覆层以检测金属构件的缺陷。对于振动筛大梁裂纹的检测，要透过包覆层检测到大梁的裂纹，可以尝试采用低频涡流技术进行检测。

低频涡流检测对仪器本身与传感器都有相应的要求，对于仪器本身由于处在低频涡流检测中，表面因素引起的涡流变化较大，所以要注意表面干扰因素对检测结果的影响。由于响应信号相位受干扰信号影响较小，所以低频涡流仪器本身应具有平面阻抗显示以方便提供相位信息，同时为了提高检测灵敏度，应具有较大的激励功率和增益。对于传感器探头，为了能增加检测深度，传感器直径一般都比较大，因为传感器产生的激励磁场透入试件的深度约为传感器直径的1／4。

根据以上理论分析，对于具有包覆层的振动筛大梁裂纹检测，低频涡流技术是可行的。然而对于带有包覆层的振动筛大梁检测目前还存在以下需要解决的问题，一是在运用低频涡流检测时，对于特定厚度、材料的包覆层和本体材料应该确定相应的适宜检测的频率段；二是运用低频涡流透过包覆层检测实现对本体裂纹大小的定量判断，针对以上问题，通过大量的试验研究，为具有包覆层振动筛大梁的快速、准确、定量的现场检测提供帮助。

2 试验研究

2.1 试验设备与试件

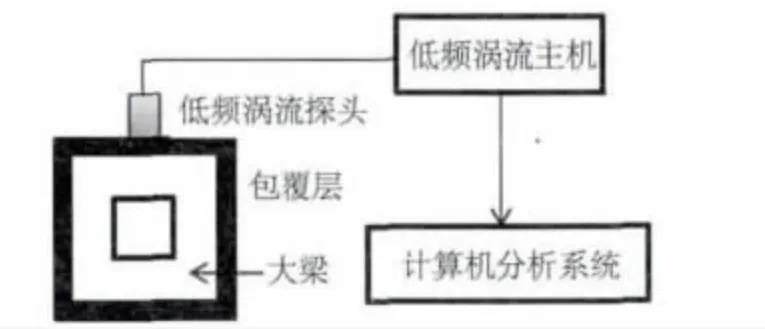
图2 测试原理图

运用低频涡流检测仪对包覆层大梁检测的测试原理见图2。试验过程中运用的设备由专用低频涡流检测仪与特制的低频涡流探头组成，试件本体材质选取的是与大梁材质一样的16 Mn钢，包覆层为现场选取的7mm 橡胶耐磨层。另外，针对振动筛大梁现场实际的检测要求，为了模拟不同大小的裂纹缺陷，分别采用线切割加工宽度为0.5 mm，深度为1mm、3mm、5mm、7mm 和10mm 的裂纹。同时，为了验证试验结论的准确性，本研究还进行了相应的现场试验。

2.2 试验数据分析

2.2.1 合适检测频率段的确定

低频涡流合适检测频率段的确定，根据涡流对比于试件上不同深度裂纹的响应情况而定。由于仪器的响应信号相位受干扰信号影响较小，通过改变试验频率，观察得到不同深度裂纹的相位响应，并通过响应信号的线性关系来确定合适的检测频率范围。由于相关系数能够很好地衡量两个变量之间线性相关的程度，为此采用相关系数及其减小误差比例来衡量不同频率范围及其响应的线性关系。相关系数r由式 （3）给出：

式中：Cov （x，y）——x 与y 的协方差；

σx——x 的标准差；

σy——y 的标准差。

从误差分析角度解释相关系数，统计学定义减少误差比例ε见式 （4）。

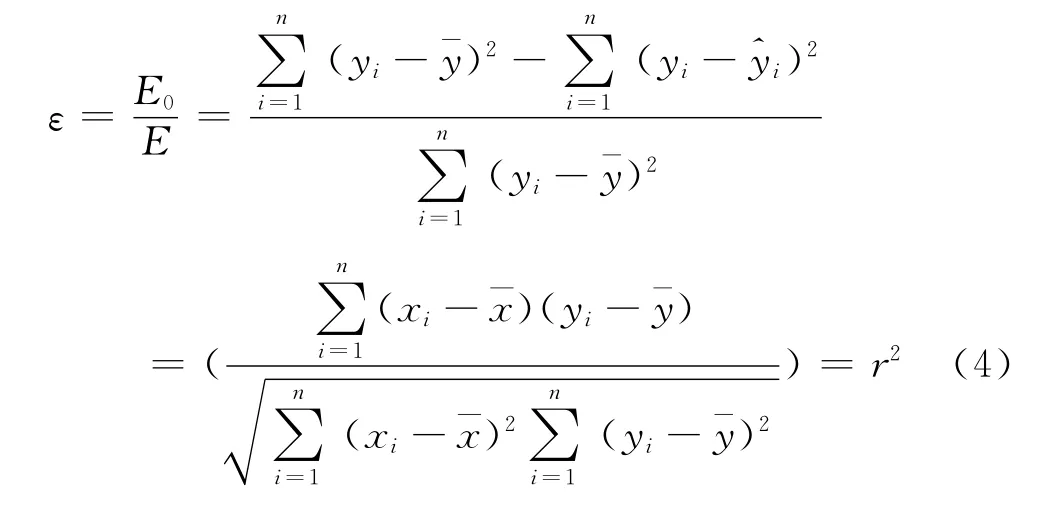
式中：E0——消减误差；

E——全部误差；

xi——第i个自变量；

yi——第i个变因量；

r——相关系数。

由式 （4）可见，r2的意义是以线性拟合方程作为预测工具时所能减小的误差比例，反映了一个量的变化中有多少是受另一个量的变化所决定的，r2越大则变量间的相关关系越密切。因此，r2不仅反映了线性相关程度，还反映了所能减小的误差比例，所以采用r2去衡量相位与频率间的关系更加完整有效。

综上所述，采用分析频率与相位的线性关系来确定合适的检测频率段，就是通过改变检测频率来观察低频涡流对于裂纹响应信号的变化，并根据响应信号的线性关系，比较r2的大小，从而确定合适的检测频率段，不同深度裂纹及不同频率下的相位值分析表见表1。

在试验检测中，当检测频率小于8kHz或大于61kHz时，检测信号的相位和幅值已经无法达到报警阈值，即无法检测与判断出裂纹信息，此时的相位值已无太大的意义，因此试验中选择8～61kHz的频率区间做检测。同时，由于深度为3mm 与7mm的裂纹处于深度为1mm、5 mm 和10mm 的裂纹范围内，且相位值以及其变化趋势基本相近，故在试验中选择了具有代表性的1mm、5mm 和10mm 的裂纹相位进行分析。其中，深度为1 mm、5 mm 与10 mm 的裂纹相位在频率8～61kHz的拟合曲线图见图3、图5和图7。深度为1mm、5 mm 与10 mm 的裂纹相位在频率12～40kHz的拟合曲线图见图4、图6和图8。

表1 不同深度裂纹及不同频率下的相位值分析表

由图3～图8对比后可以发现，不同深度裂纹在8～61kHz频率段时，尤其在接近8kHz 与61kHz时，仪器输出的相位线性关系较差，不利于裂纹信息的检测与获取；而不同深度裂纹在12～40kHz频率段时，相位的线性关系较好。然而随着检测频率区间的减小，线性关系自然会变好，因此对不同频率段的r2值进行计算比较后发现，在频率为8～61kHz时，深度为1mm、5mm 和10mm的裂纹r2值依次为0.857、0.883与0.874；在 频 率 为12～40kHz时，深 度 为1mm、5mm和10mm 的 裂 纹r2值 依 次 为0.952、0.959与0.939。

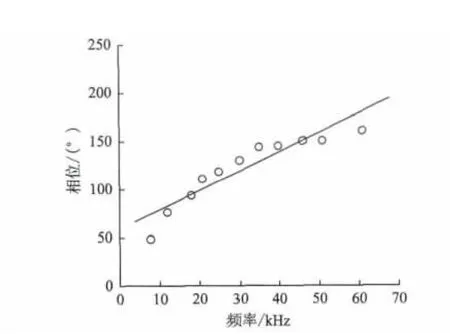
图3 深度为1mm 的裂纹相位在8～61kHz的拟合曲线

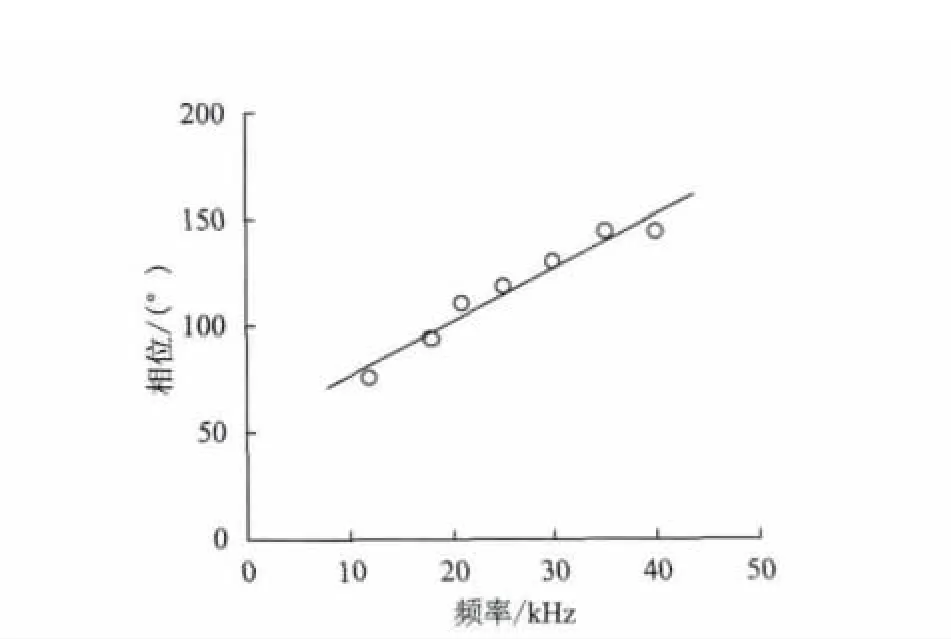
图4 深度为1mm 的裂纹相位在12～40kHz的拟合曲线

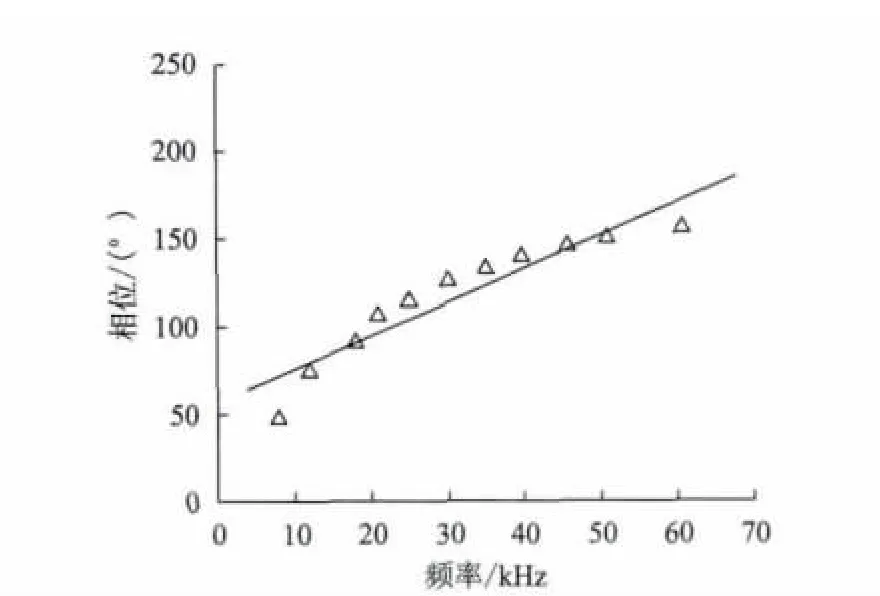
图5 深度为5mm 的裂纹相位在8～61kHz的拟合曲线

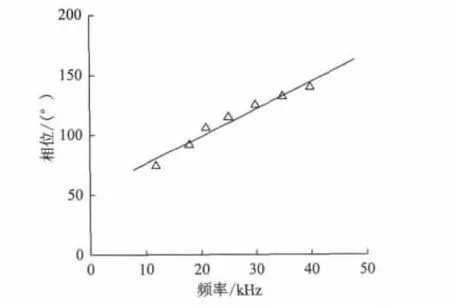
图6 深度为5mm 的裂纹相位在12～40kHz的拟合曲线

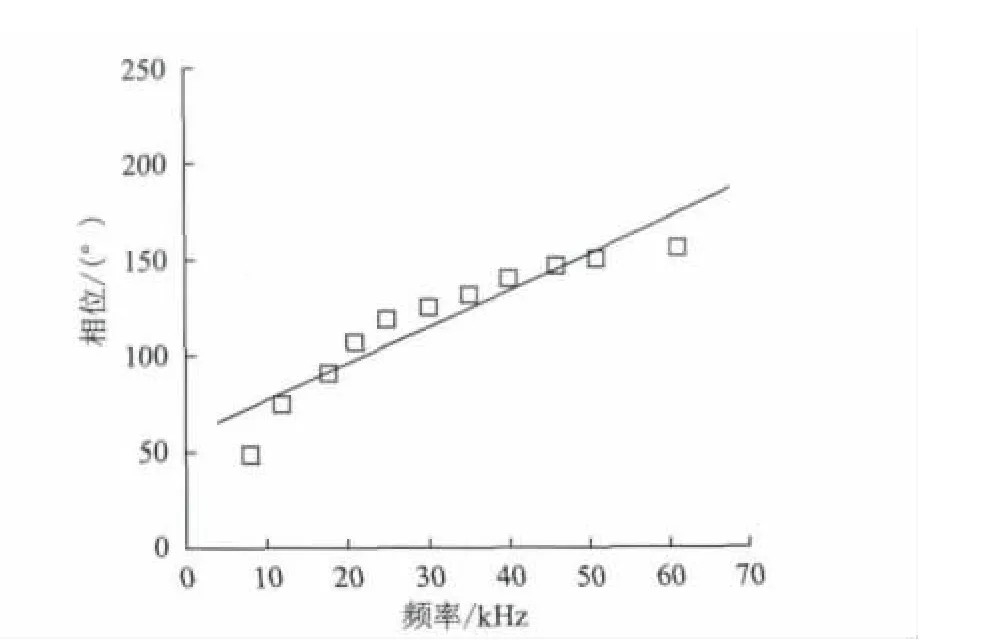
图7 深度为10mm 的裂纹相位在8～61kHz的拟合曲线

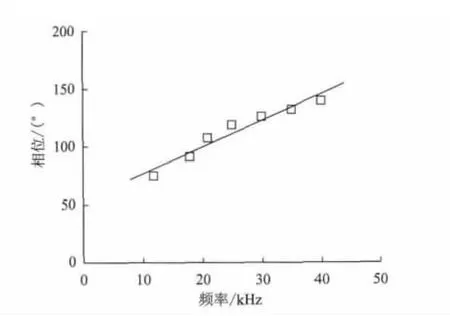
图8 深度为10mm 的裂纹相位在12～40kHz的拟合曲线

为了充分说明在12～40kHz区间的最佳性，对频率区间在18～40kHz时的r2值进行了计算，可以得到深度为1mm、5mm 和10mm 的裂纹r2值依次为0.936、0.957 与0.921。通过数据间的对比可发现，在频率为12～40kHz时，r2值比频率为8～61kHz以及18～40kHz时的值都大，说明在12～40kHz频率段下相位的线性关系和所能减小的误差比例都较好，更加有利于裂纹缺陷的发现，因此可以得出对于振动筛大梁合适的检测频率段为12～40kHz。

2.2.2 裂纹大小的定量试验

大梁裂纹大小的定量根据不同大小裂纹的低频涡流响应情况来确定，当传感器扫描到不同深度的裂纹区域时，探头感应到信号幅值明显变化，传感器靠近裂纹时，信号幅值开始变大，当传感器离开裂纹时，信号幅值开始变小。由此，可以根据传感器的响应信号幅值来判断裂纹的位置，通过对比不同大小裂纹的信号幅值特征，从而判定裂纹的深度，进而建立基于低频涡流检测的裂纹大小定量确定。本试验检测参数如下：前置为20dB、驱动为5、纠编为0、频率为21kHz、增益为30.5dB、相位为48 DEG以及包覆层为7mm 的橡胶耐磨层。

不同深度裂纹的幅值变化见图9，不同深度裂纹的阻抗变化见图10，其中图10 为运用EEC-2003+分析软件得到的裂纹阻抗图，深色区域为报警区域，线条为裂纹信号曲线。由于深度为3mm与7mm 的裂纹阻抗曲线介于深度为1mm、5mm与10mm 的裂纹阻抗曲线之间，并且变化趋势基本一致，考虑阻抗图的可观性，因此在图10中没有给出深度为3mm 与7mm 的深裂纹阻抗曲线。

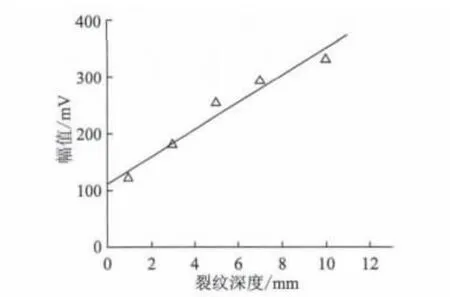
图9 不同深度裂纹的幅值变化

图10 不同深度裂纹的阻抗变化

由图9可见，响应信号幅值与裂纹深度基本呈线性关系，且随着裂纹深度的增加幅值变大。

由图10可见，随着裂纹深度的增加其报警区域内的阻抗曲线变大，即裂纹深度越深对应的阻抗幅值越大，同时也表明随着裂纹深度的增加其被检出性也更加容易。因此，综合以上这些时域特征量的分析，可以利用响应信号的幅值和裂纹深度间的试验结论，即随着裂纹深度的变大，其信号幅值也增大，同时其裂纹信号很容易被仪器获取进而检出裂纹，将裂纹深度与低频涡流信号幅值之间建立定量对应关系，根据这种定量对应关系，通过响应信号幅值的大小从而判断裂纹深度的大小。

3 结论

（1）针对目前振动筛大梁的检测具有包覆层厚的难点，将低频涡流检测运用到具有包覆层的振动筛大梁裂纹检测中，并且进行了切合实际现场的试验模拟研究。

（2）通过试验研究，得出检测频率与响应信号相位的关系，通过线性拟合确定合适的检测频率段为12～40kHz，对现场检测参数的确定具有重要的指导作用。

（3）通过试验研究，得出裂纹深度与响应信号幅值的关系，通过对线性分析与阻抗图的分析，得出裂纹深度与幅值的对应关系，对现场的实际裂纹大小定量判断具有重要的参考作用。

［1］ 薛光辉.大型振动筛大梁裂纹故障诊断方法研究［D］.北京：中国矿业大学 （北京），2009

［2］ 赵国瑞.基于振动监测的大型香蕉直线振动筛故障诊断方法研究 ［D］.北京：中国矿业大学 （北京），2007

［3］ 孙翠芝.中国选煤机械发展现状与发展方向分析［J］.中国煤炭，2012 （9）

［4］ 薛光辉，赵国瑞，朱世钢等.基于金属磁记忆和涡流检测技术的大型振动筛下横梁裂纹检测方法 ［J］.煤炭学报，2010 （7）

［5］ 徐可北，周俊华.涡流检测 ［M］.北京：机械工业出版社，2004

［6］ 任海燕，丁克勤.低频涡流检测激励频率选取的仿真研究 ［J］.无损探伤，2009 （3）

［7］ Hellier C.J.Handbook of nondestructive evaluation［M］.New York：McGraw-Hill，2003

［8］ 张玉华，罗飞路，孙慧贤.飞机轮毂涡流检测中探头提离效应的分析与抑制 ［J］.仪器仪表学报，2009 （4）

［9］ 孙红春，夏永发，崔雨.钢杆小裂纹最佳涡流检测参数的实验研究 ［J］.东北大学学报 （自然科学版），2012 （1）

［10］ 徐章韬.多种角度看线性相关系数 ［J］.数学通讯，2009 （7）