初中几何定理教学的开放性设计与有效调控方法初探

生伟

摘 要 初中几何定理教学如何处理好收和放的关系，使课堂教学发挥最大效益？在定理探索或发现多元解读处、思想方法运用的关键处、序列整合重组处进行开放设计，在学生“非标准思路”呈现需点拨时、知识的共性凸显需提炼时、在研究方向分散需集中时进行有效调控探索。

关键词 初中几何定理教学；开放性设计；有效调控；方法

初中几何定理教学是培养学生空间观念、推理能力、应用意识的重要载体，教师的引领作为引发学生学习的重要外部因素，要想最大程度地发挥作用，必须抓住时机、创造时机，唤起学生的学习积极性.在初中几何定理的教学中，我根据学生的实际情况，尝试对定理的教学进行开放性教学设计，并适时、适度进行调控，努力达到数学知识的掌握、数学技能的形成、数学思想方法的领悟和数学情感的生成相伴而行的目的，取得了较好的结果。

（1）定理证明方法往往有多种，在学生能对定理进行多元发现的交汇点进行开放设计，既提供了学生展示见解和发现的机会，促使学生个性化的解读定理，又有利于打开学生的思维空间，培养学生的发散思维.教师在学生的“非标准思路”处捕捉其独特的思维特征，并不失时机地加以点化，有利于激发学生的探究欲望、提高课堂效益。

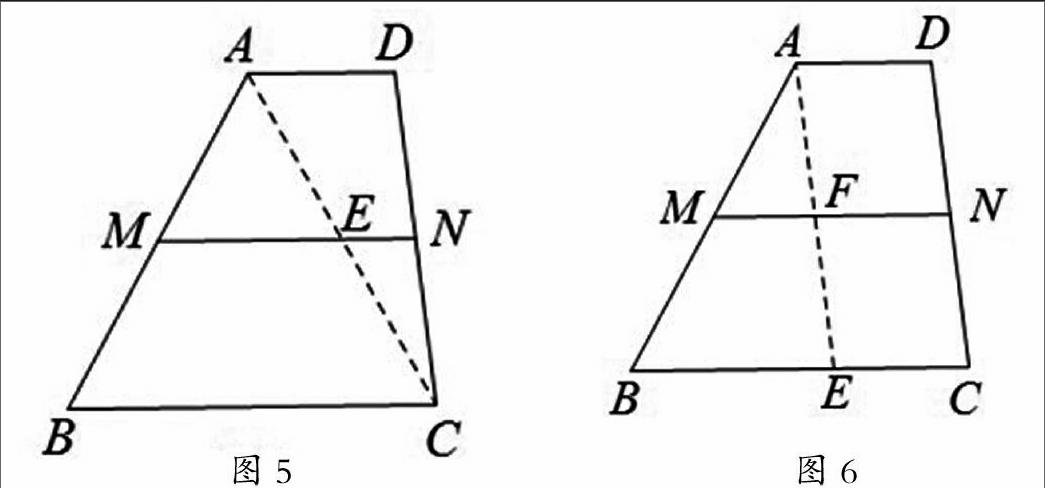
在苏科版八年级（上册）梯形中位线性质定理的证明教学中，教材设计的思路是将一张梯形硬纸片沿它的中位线剪成两部分，使分成的两部分能拼成一个三角形，让学生通过操作-观察-探索，转化为上节学过的三角形中位线的有关知识得出梯形中位线的性质（如图3）。设计意图体现就近转化.如果不拘泥于教材思路，定理的证明思路可再开阔些，学生应该有可能发现不同的证明方法.于是，作如下引导设计：问题1、通过前面三角形中位线性质的学习，你打算如何解释梯形中位线与上下底的关系？能不能转化为我们比较熟悉的内容？怎样转化？学生自己操作后，形成以下两种图形（如图2、图3）.问题2、除了利用旋转思想进行变换外，你还有没有其它方法在图形中构造三角形的中位线？引导学生转化为图5或图6进行证明。

图2、图3这两个图形是课前预设到的，大多数同学转化成图2而不是图3（因为上节三角形中位线定理证明时是按中位线剪开的！），于是，我因势利导：“同学们真的很了不起，发现了与教材不同的转化方法：把梯形问题转化为平行四边形的问题加以解决.那就用同学们发现的方法来证明吧！”学生精神振奋地投入到证明过程中.证明后，指导学生阅读教科书，比较和书上的证明思路的异同.学生自学比较，在巡视过程中，出乎意料的是，我发现一位同学构造出如图4的□EFDC，就问这位同学：“你是怎样想到的？”他说是课前预习时看到图3，想到既然能构造△ENC与△AND关于点N对称，为何不能如图4那样构造对称三角形呢？我就把他的发现重点向全班推荐，全班同学为他的与众不同而鼓掌。

【设计意图】一方面，对定理的多元化解读，课堂不能设计标准答案，不乱轻率地否定学生的探索，积极鼓励学生向书本挑战，向传统挑战，鼓励学生另辟蹊径，多视角，多层面的探索和研究问题，寻求不同答案.维果斯基认为，在进行教学时，必须注意到学生有两种发展水平：一种是他们的现有发展水平，另一种是即将达到的发展水平，这两种水平之间的差异成为“最近发展区”。教学“创造”着最近发展区.教师要设身处地从学生的角度思考问题.在我们提出的开放问题情境中，应充分注意形成展示学生展示其才能的机会和条件，使他们感到课堂有了“自由区”，这样，学生一旦充分理解所学事实的相互联系和关系，理解它的地位和意义，学生的学习兴趣和探索精神便会油然而生；一旦他从成功中得到满意，学习活动的难度、深度和期望达到的水平就会逐步提高，一般能力和个性特长才能健康的发展.另一方面，课堂要结合学生的问题来进行引导，对学生出现的信息，要迅速做出判断：“是否正确？有没有价值？是接住学生抛出的球，想出对策，对问题组织讨论？还是一两句话巧妙点拨？还是顺着学生的思路再生新枝，继续将课堂引向深入？”本节中，学生用自己的经验找到定理证明的一种转化方法，相对于我在备课时的思路和大部分同学的思路，不妨称之为“标准思路”而言，是“非标准思路”，往往更能揭示学生当前认识发展的独特状态，这种状态，既可能是学生从另一角度所作的独特思考，也可能是其思维障碍发生的关键所在.因此，教师若及时引导、点拨，由于是从学生的需要出发，容易“激活”学生思维，引起更深层次的思考.总之，让学生真切地感受到自己是学习的主人，教师只是“平等中的首席”。

（2）有时定理发现过程中蕴涵的思想方法比定理的应用更重要，可以紧扣并突出思想方法运用的关键环节，大胆放手让学生探索、思考，使其在自主参与的活动中去领悟“数学的灵魂”，教师掌握着共性凸显时“说破”的火候，从而达到下好一着棋而使满盘皆赢的目的。

在苏科版九年级（上册）圆周角定理教学中，可进一步挖掘定理发现过程中的特殊与一般的关系，而这对培养学生分析问题、解决问题的能力提高有着重要作用.我将课本中这一定理的发现过程作了延伸.为了提高课堂效率，对圆周角定理的发现进行了“浓妆重抹”：问题1：圆心角是指顶点在圆心的角，度数等于它所对弧的度数，假若顶点不在圆心的话，这个角度有何变化？在让学生自己作图实验探索以后，教师利用几何画板作出课件（如图7）.学生自己提出点P的位置要求后，教师拖动点P到不同位置，观看同弧所对角（“圆外角”、“圆周角”、“圆内角”）的变化，在学生对圆周角感兴趣后，提出圆周角的概念，引导学生在运动中观察同弧所对无数个圆周角和圆心的位置关系（圆心分别在圆周角的外部、一边上、内部），问题2：这些图形中，有没有你所熟悉的形状、大小、位置关系？学生容易发现特殊情形：圆心在圆周角的一边上，此时，同弧所对圆周角等于它所对圆心角的一半，问题3：另外两种情形是不是也符合总结出的结论？引导学生大胆猜想，作出过点P的直径，转化为圆心在圆周角的一边上来解决，从而得出圆周角定理.问题4、能否把点P的位置状态变得更“普通”些？比如“圆外角”、“圆内角”，还能有类似的结论吗？学生经过自己动手画图、小组交流，发现“普通”位置完全可以和圆周角挂起钩来.由于运动着的刺激物容易被知觉为对象，因此，学生理解了图形的演变过程，在动态中经历知识的生成过程，对于学生深刻理解定理的“来龙去脉”有着积极意义.特别是学生在一一展现自己的发现的时候的那份喜悦与自豪，令人久久难以忘怀。endprint