Goldstein枝切法对存在间断相位缺陷的解缠研究

曾凡光，吴光敏，MAI John D，陈剑鸣*

(1.昆明理工大学理学院，昆明650500;2.香港城市大学 机械与生物医学工程学系，香港)

引 言

作为干涉合成孔径雷达、光学干涉、核磁共振图像及新兴的光学非接触3维测量重建的关键步骤，2维相位解缠得到了迅速的发展和广泛的应用［1-2］。如果仅仅是将1维相位解缠的简单推广，2维相位解缠往往得不到满意的结果，因为相位解缠的结果往往与1维分割的取向、信噪比和2维采样率有着密切的关系［3］。在很多情况下，解缠误差会沿着水平或垂直的方向传递。因此，相位解缠的难点就在于如何能很好地消除误差对相位解缠的影响，来获取精确的解缠相位［4］。

目前常用相位解缠的方法可以主要归结为3类:(1)基于路径积分的相位解缠［5］;(2)基于最小范数的相位解缠［6］;(3)基于网络规划的相位解缠算法［7］。噪声或间断相位在缠绕相位中较为常见，不同的解缠算法对于噪声或间断相位引起的残差处理也不尽相同，主要包括:(1)找出优化的积分路径，避开残差点造成的误差传递［1］;(2)基于缠绕相位计算解缠相位的相位梯度估算值，将残差点造成的误差进行平差处理［6］;(3)对残差点不进行任何处理，在解缠结果中予以保留［7］;Goldstein枝切法采用第1种方式处理，找出优化的积分路径［4］，通过建立合理的枝切线，隔绝噪声区，阻止相位残差点所造成的积分误差在整幅图像中的传递。

Goldstein枝切法是在残差点电荷平衡的条件下用枝切线将附近的残差点连接起来，或者把极性相反的残差对连接在一起，或者将多个残差点对组成的集合用枝切线连接起来［4］。通常残差点与图像边界的连线也可以使残差点达到极性平衡。Goldstein枝切线的连线策略是尽量使得枝切线最短［3］。Goldstein枝切法作为典型的路径积分法，受间断相位影响很大［3］。与此同时，残差点的分布与枝切线的建立也有着紧密的内在联系。目前来看这类文献较少见到。本文中对这一问题展开专门的探讨和研究，通过模拟间断相位代替真实数据的相位跳变或缺失等问题，通过3组实验来研究不同的相位间断形式(包括单间断、双间断以及交叉双间断相位3种情况)对于解缠的影响。此外，还研究了枝切线搜索窗口半径的对解缠的影响，验证了存在“有效枝切线搜索窗口半径”的结论。

1 Goldstein枝切法相位解缠原理

从数学角度而言，解缠的目的就是要正确地将相位重建起来。1维相位解缠以一个周期内数据的连续性为前提条件的，沿着某一个方向上计算而进行的。通常干涉雷达图像数据是2维数据，通过两幅复数图像的配准计算出每一像素点上的干涉相位差。2维相位是对1维相位的扩展［8］。

给定一个2维相位矩阵φi，j，为了对该相位矩阵进行解缠，需要对每个点(i，j)加上或减去2π的整数倍值，从而得到一个连续的函数 φi，j，k为整数矩阵:

图1a中给出了1维缠绕相位，其中横坐标代表它的像素序列长度，纵坐标代表的是缠绕相位值，图1b中是图1a的解缠结果值。

图2a中给出了2维缠绕相位，其中横和纵坐标代表它的像素长度，竖直z坐标代表的是缠绕相位值，图2b中是图2a的解缠结果值。

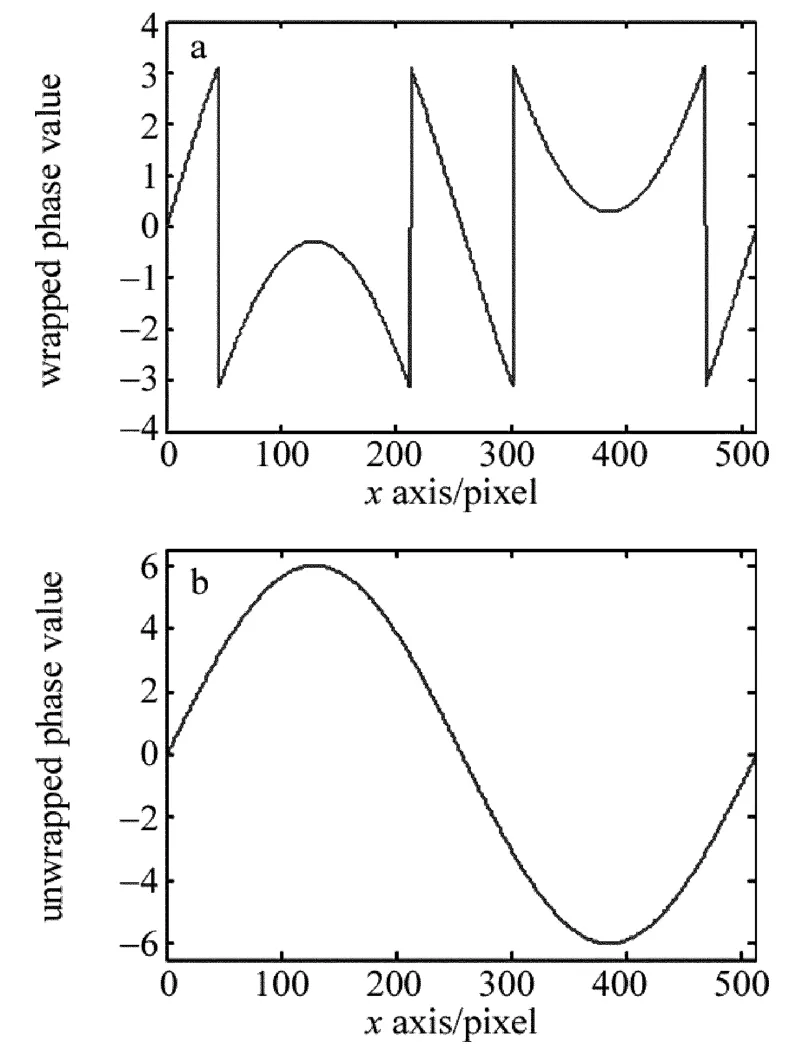
Fig.1 a—1-D wrapped phase b—1-D unwrapped phase

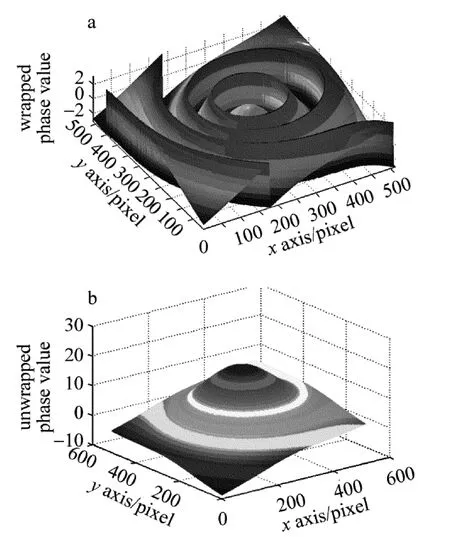
Fig.2 a—2-D wrapped phase b—2-D unwrapped phase

1.1 残差点

实际的干涉相位数据由于噪声和不连续点的影响，会出现不同路径积分的结果［9-10］。为了描述有旋分量对相位解缠的影响，引入不连续点或残差点的概念。在一幅原始缠绕数据中，定义一个2×2的窗口，以一个固定的方向，可以是顺时针或者逆时针方向，利用下面的式子计算相邻像素点之间的差值。其中q表示的4条边的像素差值和，Δ表示2×2窗口内的每条边的像素差值，W表示缠绕操作，φW表示原始缠绕相位矩阵，i和j分别为行和列值。当某一边的差值超过范围(－π，π)时，通过加减一个2π来处理，使得每条边的差值范围都保留在2π内，最后得到的值再除以2π。

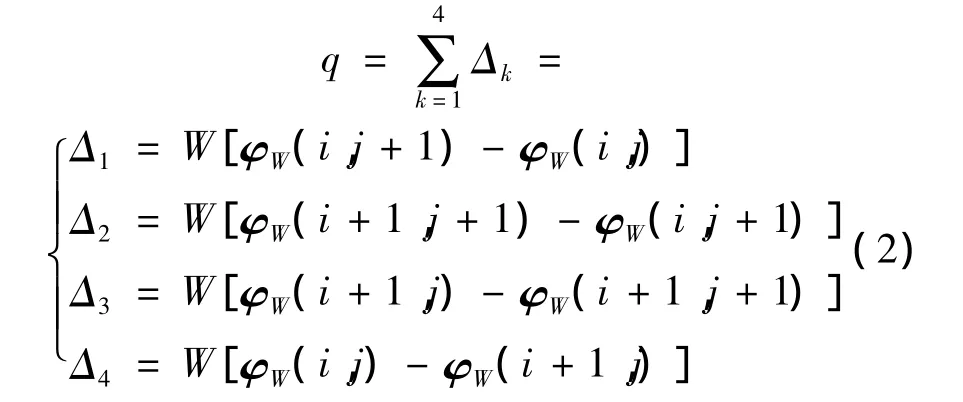
若q=0，则定义窗口内最左上角的点(i，j)上的路径为一致性路径，否则就是不一致性路径，且这个点(i，j)称为残差点。若q＞0，表示正残差点;若q＜0，表示负残差点。移动2×2窗口，直到找出整幅相位图像的残差点。

1.2 分支截断理论

分支截断理论的典型代表就是Goldstein枝切法，图3是Goldstein枝切法的流程图。通过计算相位图像的残差点，根据残差点标注的极性建立枝切线隔离区，最后通过建立的枝切线，在已知一个解缠相位点的情况下，标注出它的4个领域像素点［11］。通过建立的枝切线寻找最优积分路径，避开残差点所引起的误差传递。如果是在枝切线外，则利用已知的解缠相位点进行解缠绕，枝切线上的点留到最后进行解缠，这种积分方法也俗称洪水淹没法［12］。

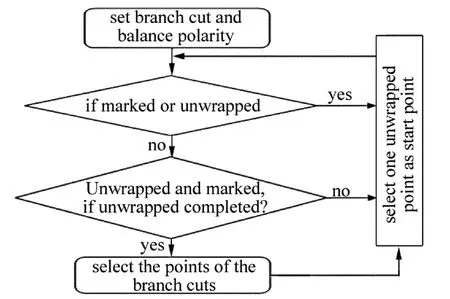
Fig.3 Flow chart of the Goldstein branch-cut algorithm

Goldstein枝切法的关键在于建立合理的枝切线，一条好的枝切线可以有效地阻断相位残差点所造成的解缠误差传递［4-5］。根据残差点的分布通常可以观察判断枝切线的放置是否有错误或存在被孤立的区域，而建立合理的枝切线又与枝切线内的搜索半径窗口有密切的关系。在枝切线搜索半径窗口设置过小，它不能穷尽搜索到所有的残差点分布;枝切线搜索半径窗口设置过大，又有可能导致连接到图像的边界，造成封闭的“孤岛”区域。

在如图4a所示的6个残差点中，黑色圆点表示负极性残差点，白色圆圈表示正极性残差点。图4b所示枝切线搜索半径窗口设置不合适，使得极性不平衡的残差点连接到图像的边界处，导致错误的枝切线。当建立图4b中的枝切线时，在两条枝切线半径之间，其残差点误差并没有完全隔离，当解缠穿越两条枝切线之间，会导致相位跳跃的情况。图4c中给出了正确的枝切线连接，这条枝切连线由于涵盖了图像中所有残差点，并且极性达到了平衡，有效地规避了残差点对解缠的影响。

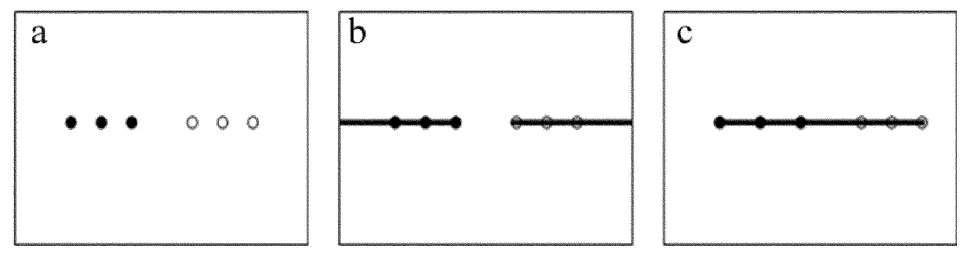
Fig.4 Branch-cut setting

2 间断相位与枝切线搜索半径的关系

为了对解缠结果进行评价，采用人工模拟的高斯模型作为实验数据，将解缠相位与真实人工相位的差值作为直观的体现，并引入了反缠绕相位均方差进行综合评判。

（1）严格区分煤矿关闭和企业破产。煤矿关闭是行政行为，而企业破产是法律行为，二者政策大不相同。国内煤矿关闭和企业破产之间没有严格的区分，安置措施缺乏针对性。

反缠绕相位均方差是将相位进行反缠绕［13］，把求得反缠绕相位和原始缠绕相位的均方差σ作为解缠精度评价的指标之一，其中σ为:

式中，φW为原始缠绕相位矩阵，ψW为解缠相位经过再次缠绕计算得到的相位矩阵;M，N为图像的行列数。该指标实质是评价解缠前后的主相位值的保持性。

2.1 单间断相位情况

在模拟高斯模型数据时，原始人工图的大小为512pixel×512pixel。人工切割只有单间断相位缺陷，并考虑在不同切割高度和切割深度的情况下，枝切线搜索窗口半径的变化关系。

在切割高度为50pixel，切割深度为80pixel的情况时，计算它的有效枝切线搜索窗口半径，如图5所示。图5a中给出了单间断相位缺陷的2维显示，图5b中给出了单间断相位缺陷的3维显示，图5c中给出了单缠绕相位缺陷的灰度2维显示。

Fig.5 Gaussian distribution models for the single phase discontinuity

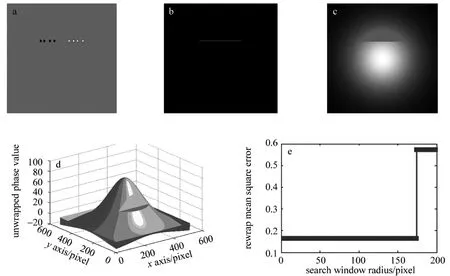
Fig.6 Goldstein branch-cut unwrapped result of the single phase discontinuity

通过计算发现，当枝切线搜索窗口半径处于65pixel～174pixel之间的任意一处值时，可以得到精确的解缠结果。图6a是残差点分布图，图6b是枝切线连线图，图6c是解缠相位的2维显示图，图6d是解缠相位的3维灰度显示图，图6e是反缠绕均方差曲线图。其中横坐标表示的窗口半径是枝切连线中寻找残差点平衡时的窗口的半径大小。从以上结果可以直观看出，Goldstein枝切法能正确建立枝切线，获得正确的解缠相位。从解缠相位与真实相位的差值图也可以看出，在大部分区域中的解缠误差为0。而在图像的边缘，由于只存在三领域，故在解缠时都被赋值为0，不参与解缠过程。在均方差与枝切线半径的曲线图(见图6e)中，横坐标表示枝切线搜索窗口的半径大小，纵坐标表示反缠绕相位均方差的值。从图6e中可以清楚地看出，在枝切线半径范围为65pixel～174pixel时，反缠绕相位均方差的值为0.1621。在枝切线搜索窗口半径大于174pixel时，反缠绕相位均方差的值跳跃为0.5714。注意到在半径小于65pixel时，反缠绕相位均方差的值仍然为0.1621，这主要与解缠结果有关。在枝切线半径小于65pixel时，在间断相位处，解缠结果有2π相位值的跳跃变化，而在计算反缠绕相位均方差值时，需要将解缠相位重新缠绕后再进行计算，因此这里的2π相位值的跳跃变化不影响总体的反缠绕相位均方差值。

对于不同的切割高度和切割深度，有效枝切线搜索半径大小范围有所变化，在切割高度为40pixel，切割深度为40pixel时，枝切线搜索半径窗口设置在73pixel～148pixel之间时，能够得到正确的解缠相位。通过不同大小的切口计算得到的规律为:切口越大，能够解缠的有效搜索半径的下限值就越大，而上限值由枝切线是否与边界接触确定。当枝切线连接到图像的边界，如果此时没有搜索完所有的残差点，遗留下未搜索的残差点容易引起解缠误差。如果已经搜索完所有的残差点，而此时连接到图像边界的枝切线如果没有形成一个不可解缠的“孤岛区域”，此时仍可以得到正确解缠。如果形成了一段封闭的“孤岛”区域，此时解缠依然会有误差。

2.2 双间断相位情况

首先讨论有两处不相交的切割间断相位的情况。在两处切割高度分别为60pixel和50pixel，切割深度都为80pixel时，如图7所示。图7a是两处间断相位缺陷的2维显示，图7b是两处间断相位缺陷的3维显示，图7c是缠绕两处相位缺陷的灰度2维显示。由于两处切割的距离为160pixel，故这里的枝切线半径窗口上限设置为160pixel。当超过160pixel时，枝切线搜索窗口容易连接到另一处间断相位的残差点，形成局部不可解缠的“孤岛”区域。由前面计算得知，在切割高度为50pixel时，它的有效枝切线搜索半径为65pixel～174pixel。在切割高度为60pixel，切割深度为80pixel时，有效枝切线搜索半径不小于89pixel。由于搜索窗口的变化步长一般为2pixel，为了方便确定搜索窗口内中心残差点坐标，一般的搜索半径窗口都是奇数，因此搜索半径的最大值应该为157pixel，由于158pixel的搜索窗口中心和157pixel是一样的，故这里设置158pixel。

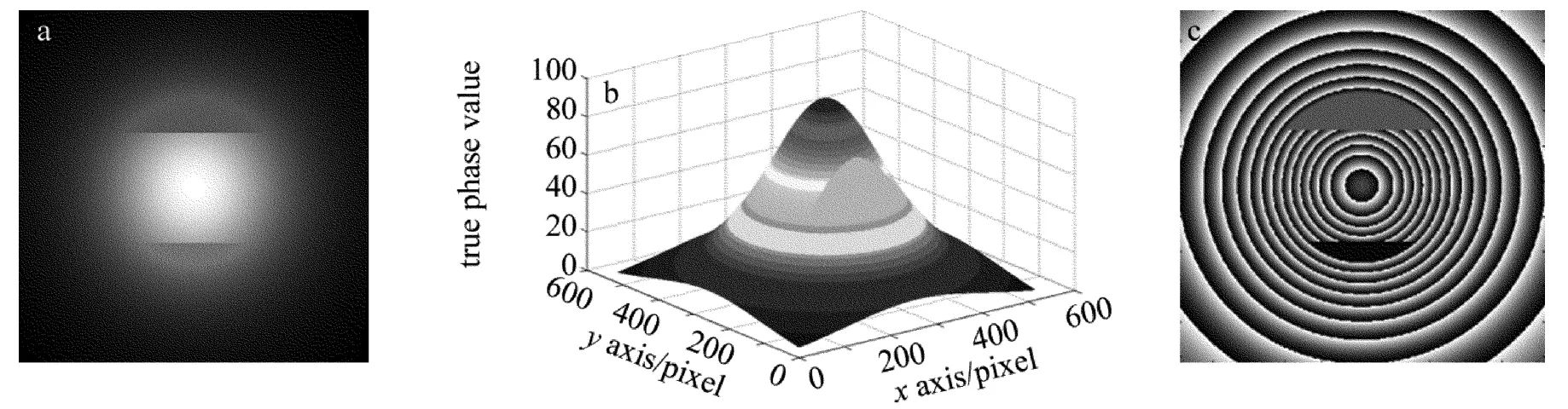
Fig.7 Gaussian distribution models for the two disjointed phase discontinuities

Fig.8 Goldstein branch-cut unwrapped result for two disjoint phase discontinuites

经过实际计算可知在枝切线半径处于89pixel～158pixel之间，对于两处不相交的间断相位能够正确解缠，在枝切线搜索半径处于这个范围之外，解缠结果会有误差。图8a是残差点分布图，图8b是枝切线连线图，图8c是解缠相位的2维显示图，图8d是解缠相位的3维灰度显示图，其中横纵坐标表示像素点个数，竖直轴表示解缠相位值，图8e是反缠绕均方差曲线图，横坐标代表的是枝切线搜索窗口的半径。从均方差与枝切线半径的曲线图(见图8e)可以看出，在枝切线半径大于158pixel时，它的反缠绕均方差显著增大，而在有效枝切线半径范围内，它的值固定在0.1621。

当两处不相交的间断相位切割高度同为50pixel，切割深度同为80pixel时，它的有效枝切线搜索半径范围为65pixel～158pixel。这说明在有两处不相交的间断相位时，如果事先知道每处间断相位能够正确解缠的枝切线范围，并且已知两处间断相位的像素距离，便可计算在两处单独有效的枝切线搜索半径的交集而获得的枝切线的有效范围。

如果两处间断相位发生了相交，解缠将会变得困难。图9中给出了两处间断相位垂直相交的情况，图9b中的横纵坐标表示相位像素点坐标，竖直z轴表示的是它的真实相位值。解缠的结果如图10所示。

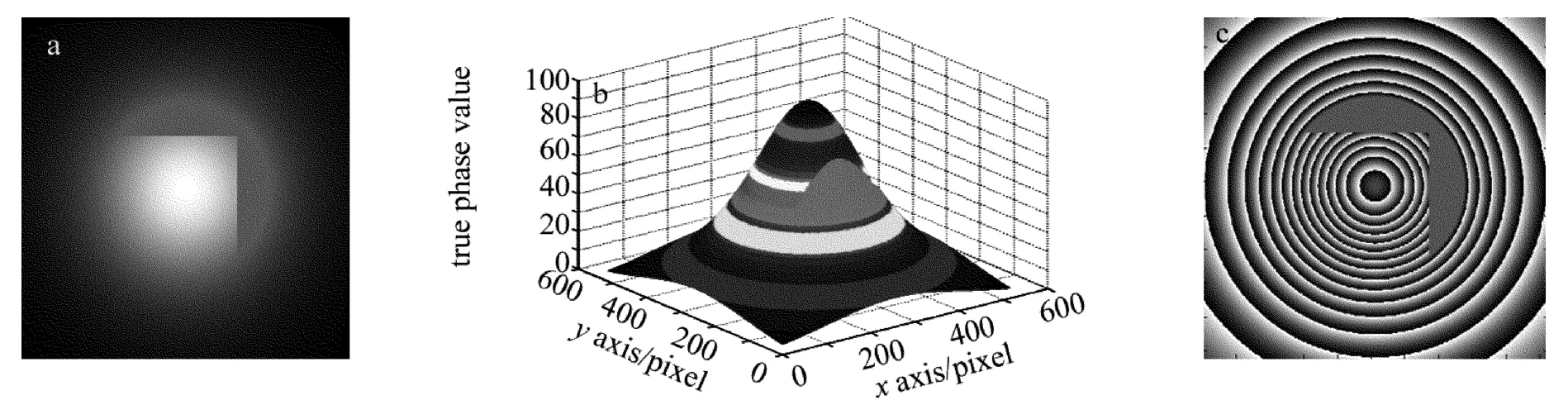
Fig.9 Gaussian distribution models of the two intersecting phase discontinuities

Fig.10 Goldstein branch-cut unwrapped result for two intersecting phase discontinuities

图10a是残差点分布图，图10b是枝切线连线图，图10c是解缠相位的2维显示图，图10d是解缠相位的3维灰度显示图，其横纵坐标表示像素点坐标值，竖直z轴表示解缠相位值。从解缠相位与真实相位的误差图(见图10e)中可以看出，解缠结果中存在一个明显的三角形的误差区域。在均方差曲线图(见图10f)中，横坐标代表枝切线搜索残差点窗口的半径大小，纵坐标代表计算得到的反缠绕均方差值。由于误差引起的均方差存在着起伏跳跃式变化，无论它们的切割高度和切割深度是否相同，两处间断处都含有分布较为紧密的残差点。尤其在间断相位相交处，非常容易形成不可解缠的“孤岛”区域，使得总体解缠结果有误差。枝切线搜索半径设置过大，容易连接间断相位处的所有残差点，造成由多条枝切线形成的封闭区域。如果枝切线搜索半径过小，容易造成残差点的未完全隔离，导致解缠误差的全局传递。从所讨论的情况来看，很难找到一个合适的枝切线搜索半径能够建立合理的枝切线，隔离所有残差点的误差，避免误差传递。

3 结论

(1)在单相位间断缺陷和双不交叉的相位间断缺陷的情况下，Goldstein枝切法仍然具有较好的解缠效果。

(2)对于双交叉相位间断缺陷，Goldstein枝切法在这一局部区域无法得到正确的解缠结果。

(3)不同的间断相位缺陷对应着不同的有效枝切线半径范围。在双不相交切割间断相位的情况时，可以根据有效枝切线半径的交集得到正确的解缠结果;而在双相交切割间断相位的情况时，Goldstein枝切法无法得到有效的枝切线半径范围，也就无法得到正确的解缠相位。由此可以得出，Goldstein枝切法解缠存在着有效枝切线半径。当枝切线搜索半径处于有效范围之外，解缠结果一般都存在误差。

本文中的实验结果对于采用或联合采用Goldstein枝切法进行的相位解缠理论研究和应用具有参考价值。

［1］ LI B，QIAN X F，LI X H，et al.Phase-unwrapping algorithm based on radial shearing principle［J］.Laser Technology，2013，37(1):44-47(in Chinese).

［2］ YANG F T，LUO J L，LIU Z Q，et al.Comparison of six phase unwrapping algorithms［J］.Laser Technology，2008，32(3):323-326(in Chinese).

［3］ GHIGLIA D C，PRITT M D.Two-dimensional phase unwrapping:theory，algorithms，and software［M］.New York，USA:Wiley，1998:103-121.

［4］ GOLDSTEIN R M，ZEBKER H A，WERNER C L.Satellite radar interferometry:two-dimensional phase unwrapping［J］.Radio Science，1988，23(4):713-720.

［5］ ITOH K.Analysis of the phase unwrapping algorithm［J］.Applied Optics，1982，21(14):2470-2470.

［6］ BONE D J.Fourier fringe analysis:the two-dimensional phase unwrapping problem［J］.Applied Optics，1991，30(25):3627-3632.

［7］ COSTANTINI M.A novel phase unwrapping method based on network programming［J］.IEEE Transactions on Geoscience and Remote Sensing，1998，36(3):813-821.

［8］ FLYNN T J.Two-dimensional phase unwrapping with minimum weighted discontinuity［J］.Journal of the Optical Society of A-merica，1997，14(10):2692-2701.

［9］ OESCH D W，SANCHEZ D J，TEWKSBURY-CHRISTLE C M.Aggregate behavior of branch points-persistent pairs［J］.Optics Express，2012，20(2):1046-1059.

［10］ HANSSEN R F.Radar interferometry:data interpretation and error analysis［M］.Dordrecht，Netherlands:Kluwer Academic Publishers，2001:22-23.

［11］ BAO Zh，XIN M D，WANG T.Radar imaging technology［M］.Beijing:Publishing House of Electronics Industry，2005:310-311(in Chinese).

［12］ ASUNDI A，WENSEN Z. Fast phase-unwrapping algorithm based on a gray-scale mask and flood fill［J］.Applied Optics，1998，37(23):5416-5420.

［13］ LEI S，ZHANG S.Digital sinusoidal fringe pattern generation:defocusing binary patterns vs focusing sinusoidal patterns［J］.Optics and Lasers in Engineering，2010，48(5):561-569.