自由式滑雪运动员曲线滑道段内空气动力特性的CFD研究

夏娇阳，韩秀华，马毅，王新

自由式滑雪运动员曲线滑道段内空气动力特性的CFD研究

夏娇阳1，韩秀华2，马毅3，王新4

目的：为了探讨自由式滑雪空中技巧运动员在跳台上滑行时的空气动力学特征，为出台速度的计算提供空气动力学参数。方法：根据逆向建模理论，对我国自由式滑雪运动员徐梦桃在曲线滑道中所受的空气动力特性创建自由式滑雪运动员曲线滑道段内的实体模型，在此基础上，利用三维虚拟设计软件建立运动员绕流流场的空间模型，并用CFD方法模拟运动员于曲线滑道中的绕流流场。结果：在曲线段，运动员所受的升力可忽略，而阻力值相对较大不能忽略；出台斜坡和立壁的角形区域内会形成涡流区。结论：（1）证明了CFD方法在研究自由式滑雪助滑阶段空气动力特性研究中的有效性；（2）在出台斜坡和立壁的角形区域内形成的涡流区对运动员起跳出台的速度以及稳定性有负面的影响；（3）临近曲线滑道末端时，空气阻力与运动员自身重力的切向分量相当，因此会产生较大的切向加速度，在阻力和自身重力切向分量共同叠加下，运动员的滑行速度会迅速衰减。

自由式滑雪空中技巧；曲线滑道；升力；阻力；CFD

自由式滑雪空中技巧是冬季奥运会常设比赛项目，我国运动员韩晓鹏曾于第20届都灵冬奥会夺得该项目的金牌，实现了冬奥会历史上我国雪上项目金牌零的突破，徐梦桃借助其高难度动作获得了索契冬奥会女子自由式滑雪空中技巧项目的银牌。自由式滑雪空中技巧由助滑、起跳、腾空翻转和落地4个阶段组成，比赛中运动员借助3.5～4 m的跳台起跳，在腾起高度达到15 m左右之后的下落过程中完成一系列的翻转动作，最终在37°的斜坡上着陆。自由式滑雪空中技巧项目的评分主要根据腾空翻转和落地阶段的完成质量来决定。所以，国内外相关研究多集中在腾空翻转和落地阶段，助滑和起跳阶段的研究则鲜有人问津，而且由于恶劣的场地环境以及试验手段和测试技术所限，国内外尚未见曲线滑道这方面的研究报道。随着计算机软硬件的飞速发展，CFD（computational fluid dynamics）方法日益成为复杂流体流动，甚至是流—固耦合传热、传质问题研究的主要方法和手段[1-3]。本文采用CFD理念和方法，研究曲线段滑道内我国自由式滑雪空中技巧优秀运动员的空气动力特性，为模拟再现运动员助滑阶段的运动过程奠定基础。

1 研究对象与方法

1.1 研究对象

运动员实体化模型的建立，一直是制约自由式滑雪助滑阶段空气动力特性CFD研究的瓶颈。根据逆向建模理论，采用激光三维扫描仪对我国优秀自由式滑雪空中技巧运动员徐梦桃（女，身高1.65 m，体重（含装具）63 kg，运动员迎风面的投影面积为0.676 935 m2）进行扫描，得到多达20余万个点的点云数据，在三维虚拟设计软件中经小平面建模、修补破面及实体化等过程建立运动员三维实体模型（运动员表面被分割为87个无缝连接的曲面片）（见图1）。

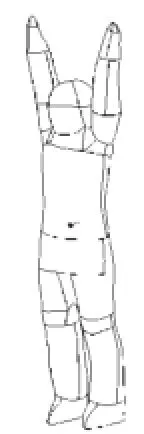
图1 运动员实体模型Figure1 Athletes physical model

1.2 研究方法

采用CFD理念和方法，对徐梦桃助滑曲线段的空气动力特性进行研究，模拟再现运动员助滑阶段的运动。试验时间为2013年备战索契冬季奥运会的专项准备阶段，试验场地为吉林省北大湖滑雪场自由式滑雪空中技巧国家队训练场地，数据采集为3周台滑道，试验数据由沈阳体育学院运动人体科学学院生物力学实验室采集并分析。

2 结果

2.1 CFD模型

CFD是伴随着计算机技术、数值计算技术的发展而发展的，CFD相当于模拟仿真实际的流体流动情况，其基本原理是数值求解控制流体流动的微分方程，得出流体流动的流场在连续区域上的离散分布，从而近似模拟流体流动情况。ADINA是CFD软件之一，以有限元理论为基础，通过求解力学线性、非线性方程组的方式获得固体力学、结构力学、温度场问题的数值解，该软件在计算流—固耦合流场计算中的性能优良。自由式滑雪的滑雪道是由直线下降段、平直段和曲线段组成，其中曲线段的曲线方程在国内外文献中鲜有详实报道，根据实测结果经多项式拟合得到的助滑道曲线段的曲线方程为：

式中：χ为横向坐标；y为纵向坐标；a1=0、a2=4.4×102、a3=1.3×105、a4=5.4×108、a5=1.6×1011、a6=1.6×1015。

R（相关系数）=0.999 98，SD（拟合标准差）=0.013 39，N（数据点）=20，P<0.013 39。最终，采用三维虚拟设计中的插入/合并与继承功能模块，建立了运动员绕流流场空间模型（为了节省计算成本，去除了滑道的直线下降段）。该运动员滑行到曲线段6.752 m处时的绕流流场空间模型见图2（该点曲率半径为3.09 m，该点滑道切平面与水平面的夹角为117.291°）。

图2 CFD计算模型Figure2 CFD computing model

2.2 CFD仿真研究

运动员所受的空气动力是空气施加于运动员的压力和摩擦力的合力，该合力可通过求解运动员绕流流场来求得。由于运动员复杂的外形和褶皱不平的表面，所以运动员贴体附近流场必为湍流流场，而离运动员较远的区域则应为层流流场，故宜采用在层流和湍流混合流场计算中表现优异的k—ωSST双方程湍流模型[4-5]，并采用有限元法[6]求解该湍流模型方程。将图3所示的绕流流场空间模型进行网格划分（划分为4面体4节点单元32万余个），考虑到贴近运动员表面的附面层内较大的速度梯度以及凸凹不平的运动员表面，网格划分时特意在运动员表面加密了网格（见图3）。程序中，运动员表面和雪道均被定义为不可穿透的壁面（运动员表面为移动壁面），其余的表面则为开放的表面（与实际相符）。假设比赛环境温度为-20°，则空气的密度和动力粘度分别为1.395 kg/m3、1.62×10-5Pa·s。与直线滑道中运动员进行平动的情形所不同的是，在曲线滑道中运动员是绕其瞬心转动，这个瞬心便是不断变化的曲线滑道的曲率中心。所以，在本文的研究中将运动员的运动设置为绕滑道曲率中心（即瞬心）的转动。

图3 网格划分示意图Figure3 Schematic diagram of grid division

2.3 曲线滑道段内空气动力学特征

分别计算了角速度为6、7、8、9、10、11、12°/s时的运动员绕流流场。角速度为8°/s时的若干纵剖面的速度分布图显示，各个纵剖面中速度分布均呈不均匀的特性（其中z=0的纵剖面与运动员的正中矢状面相重合）（见图4）。

图4 纵剖面速度矢量图Figure4 Longitudinal velocity vector diagram

经多项式拟合法得到的运动员升力和阻力与滑行速度之间的关系曲线和方程显示，升力和阻力均随运动员滑行速度的增加而非线性地增加，曲线是下凹的，故而随着运动员滑行速度的增加，升力和阻力增加的也越快，升力较之阻力而言要小一个数量级。若滑行速度为20 m/s，阻力和升力分别约为220 N和12 N，而此时自身重力（含装具）的切向和法向分量分别约为548 N和283.07 N（见图5、图6）。

图5 升力与滑行速度之间的关系曲线和方程Figure5 Curve and equation between lift and sliding velocity

3 分析与讨论

完美的起跳能保证完成腾空和翻转所需要的足够腾空高度和稳定性，而助滑阶段则是保障运动员完美起跳的关键。在助滑过程中，运动员姿势要由最初的马步状出发姿势适时地演变为双臂直举、身体直立的出台姿势（在曲线滑道段，运动员基本上保持图1所示的姿势不变）（见图7）。掌控助滑阶段，尤其是曲线滑道段内运动员所受的空气动力特性对于完成高质量的起跳具有重要的意义。

图6 阻力与滑行速度之间的关系曲线和方程Figure6 Curve and equation between resistance and sliding velocity

图7 滑道中运动员姿势演变图Figure7 Athletes posture slideway evolution diagram

尽管运动员的滑行速度较大，但由于除雪道外的其他壁面为开放的壁面，所以运动员所卷带的周围空气的流动速度较之运动员滑行速度而言是微乎其微的。当运动员临近滑道尽头时，受运动员驱动的影响，运动员即将投身的空间区域内形成了与运动员滑行速度同向的气流流动，而在运动员即将出台的斜坡和立壁的角形区域内则形成了涡流，这对运动员的平稳出台会有消极的影响，是运动员能否成功起跳、起跳高度如何的重要因素。从技术角度考量，运动员出台起跳时的技术影响因素主要包括出台速度、体位角度以及足底压力[7]3个主要方面。在训练和比赛中，助滑速度越快可致使出台速度增加，但是可导致运动员出台的稳定性差。运动员体位角度的减小可以减少迎风面积，重心位置的降低可减少涡流对出台技术的影响。与前人[8]研究结果一致，体位角度增大势必会造成重力矩增大，导致垂直于起跳方向的力的分量减小，在使运动员在空中绕横轴的翻转速度加大的同时，减小了速度的垂直分量，从而使腾空高度降低。

升力较之自身重力的法向分量而言要小得很多，所以升力可忽略。雪板与滑道之间的摩擦力主要是由自身重力的法向分量和离心力而引起的，阻力则与自身重力的切向分量相当，强大的空气阻力与自身重力切向分量的双重作用下，运动员切向加速度可达-12.2 m/s，因此，运动员的滑行速度在曲线滑道的末端会迅速降低。

4 结论

根据逆向建模理论，在创建了自由式滑雪运动员在曲线滑道段内的实体模型的基础上，利用三维虚拟设计软件建立了运动员绕流流场的空间模型，并用CFD方法模拟了运动员于曲线滑道中的绕流流场，证明了CFD方法在研究自由式滑雪助滑阶段空气动力特性研究中的有效性。结果表明：在出台斜坡和立壁的角形区域内形成了涡流，其对运动员起跳出台速度以及稳定性有着负面的影响；临近曲线滑道末端时，空气阻力与运动员自身重力的切向分量相当，因此会产生较大的切向加速度，运动员滑行速度的衰减非常明显。

[1] 刘丹，陈凤馨.CFD在计算船舶螺旋桨敞水性能中的应用研究[J].现代制造工程，2010（4）：18-20．

[2] 赖华威，刘月琴，吴家鸣.基于CFD方法的螺旋桨性能计算与分析[J].船海工程，2009，38（4）：131-135．

[3] 胡健，黄胜，王培生.螺旋桨水动力性能的数值预报方法[J].江苏科技大学学报，2008，22（1）：1-6．

[4] 雷延生，周正贵.风力机振荡翼型动态失速特性的CFD研究[J].太阳能学报，2010，31（3）：367-372.

[5] 周宇，钱炜祺，邓有奇，等.k-ωSST两方程湍流模型中参数影响的初步分析[J].空气动力学，2010，28（2）：213-217.

[6] 章本照，印建安，张宏基.流体力学数值方法[M].北京：机械工业出版社，2003.

[7] 王新，马毅，郝庆威，等.自由式滑雪空中技巧技术诊断体系的研究[J].沈阳体育学院学报，2011，30（2）：4-7.

[8] 马毅，闫红光，吴志海，等.影响自由式滑雪空中技巧动作难度的相关因素分析[J].沈阳体育学院学报，2010，29（1）：8-11.

CFD Study on Aerodynamic Characteristics of Freestyle Skiing Athletes in the Curve Slideway Period

XIA Jiaoyang1，HAN Xiuhua2，MA Yi3，WANG Xin4
（1.Dept.of PE，China University of Petroleum，Qingdao 266580，China；2.Harbin Institute of Technology，Harbin 150001，China；3. Shenyang Sport University，Shenyang 110102，China；4.Dept.of Human Sports Science，Shenyang Sport University，Shenyang 110102，China）

Objective：In order to explore the aerodynamic characteristics of athletes in the aerials event of freestyle skiing sliding on the platform，and provide aerodynamic parameters for the calculation on leaving platform speed.Methods：According to the reverse modeling theory，the model of aerodynamic characteristics of Chinese freestyle skier，Mengtao Xu，in the curve slideway period was established.Based on the entity model and by using 3D virtual design software，a space model of the flow field around was created，and CFD method was used to simulate the flow field around a curve slideway.Results：The lift of athletes in the curve slideway period can be neglected，and the resistance can not be neglected because it is relatively large.In addition，there was an eddy zone which formed by the slope on leaving platform and the angle area of the vertical wall.Conclusions：The study demonstrated that the CFD method is effective on the study of sliding period aerodynamic characteristics in Freestyle Skiing.The eddy zone which formed by the slope on leaving platform and the angle area of the vertical wall made a negative impact on the athletes take off speed and stability.Near the end of curve slideway，air resistance and athlete weight were tangential component，and therefore a larger tangential acceleration was created.With the common superposition of resistance and own gravitational tangential component，the athletes sliding speed will decay rapidly.

freestyle skiing aerials；curve slideway；lift；resistance；CFD

G 804.6

A

1005-0000（2014）03-190-03

2014-01-06；

2014-04-22；录用日期：2014-04-23

国家自然科学基金项目（项目编号：11102120）

夏娇阳（1978-），女，黑龙江齐齐哈尔人，博士，副教授，研究方向为冬季竞技体育运动。

1.中国石油大学（华东）体育教学部，山东青岛 266580；2.哈尔滨工业大学体育部，黑龙江哈尔滨 150001；3.沈阳体育学院院长办公室，辽宁沈阳 110102；4.沈阳体育学院运动人体科学系，辽宁沈阳 110102。