基于响应面法的高强度钢板热冲压成形圆角破裂的工艺参数优化
王梦寒,王彦丽,杨海
(重庆大学 材料科学与工程学院,重庆,400030)
高强度钢板热冲压成形过程繁琐,零件形状复杂,尤其是带有圆角的零件,稍有不慎将会造成圆角的破裂,影响使用安全性能。图1 所示为某车型汽车加强件热冲压过程中的圆角发生破裂的典型案例,零件圆角处于温度骤变及传力区,致使塑性降低,发生β 破裂。在高强度钢板热成形材料损伤方面,Skår 等[1]利用无损检测技术研究分析了U 形件热冲压成形过程中的磨损和破裂问题;Drillet 等[2]观察分析了热冲压成形件破裂过程中的微观组织变化;张志强[3]利用数值模拟技术分析了B 柱热冲压成形过程中板料厚度的变化规律。以上研究只是单纯的分析热冲压成形中钢板产生破裂的原因和工艺参数的影响规律。而通过优化相关工艺参数来避免热冲压成形件产生破裂的研究比较少。针对图1 所示的汽车加强件热冲压成形的破裂现象,论文利用Dynaform 模拟软件对其进行模拟,分析圆角发生破裂的原因,采用响应曲面法研究影响高强钢板成形质量的主要因素,以期获悉避免圆角破裂的最佳热冲压工艺参数条件组合。

图1 某车型汽车加强件零件图Fig.1 A model auto reinforcement detail drawing
1 基于响应面法高强度钢板厚度减薄率目标函数的构建
高强度钢板热冲压成形中板料破裂可以通过板厚的减薄率直接形象的表现出来,只要减薄率控制在允许的范围之内就不会出现破裂问题。图1 中的热冲压件形状复杂,存在B 和C 2 个不对称圆角,需要利用线性加权法得到高强度钢板圆角厚度减薄率的总目标函数。B 和C 圆角最大减薄率的计算公式分别为:
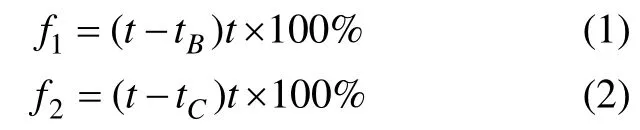
式中:f1和f2分别为B 和C 圆角的最大减薄率,%;t为板料原始厚度,mm;tB和tC分别为B 和C 圆角最小壁厚,mm。
对高强度钢板厚度减薄率进行响应分析的总目标函数为
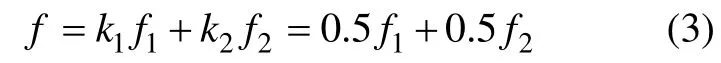
式中:f 为热冲压件的圆角厚度减薄程度(目标值),%;k1+k2=1,k1和k2为加权系数[4],热冲压件的2 个圆角有一定的关联性,处于同等重要的地位,取k1=k2=0.5。
响应面分析法(MSR)利用试验设计及数学知识,建立目标与影响因素之间的高度非线性模型,并通过不断的迭代试验,实现目标的收敛。响应模型中影响因素和目标函数的关系式[5-6]为

式中:ε 为综合误差项;f(x)为目标函数的近似响应模型,可表述为

n 为变量维数;βi,βii和βiii分别为一次、二次、三次基函数多项式回归系数;xi(i=1,…,n)和xj(j<i)为影响因子是第i,第j 的设计变量。
数值模拟中以成形极限图作为板料破裂和起皱的判断依据,满足约束的条件是板料的每个成形单元的应变值都处于破裂和起皱之间的安全区域。为了计算目标值,完成目标函数的构建,对加强件热成形过程进行模拟。
2 加强件成形过程仿真分析
论文使用宝钢生产的含硼高强度钢BR1500HS,板厚1.8 mm。通过热模拟实验[7-8]得到高强度钢板热冲压模拟分析所需数据,图2 所示为板料的真应力-真应变曲线,表1 和表2 所示分别为不同温度下的热膨胀系数和热传导系数。

图2 流变应力-应变与温度和应变速率的关系曲线Fig.2 Influence of temperature and strain rate on flow properties of BR1500HS

表1 不同温度下的热膨胀系数Table 1 Thermal expansion coefficient at different temperatures

表2 不同温度下的热传导系数Table 2 Heat conduction coefficient at different temperatures
在板料温度为750 ℃,压边力为80 MPa,摩擦因数为0.2 的初始条件下进行模拟,零件的成形极限见图3,成形结束时的厚度分布见图4。由图3 可以看出:零件的2 个圆角区域均出现了破裂现象,破裂位置与图1 所述实际生产破裂位置一致,即图1 的B 和C 处。

图3 圆角破裂件的成形极限图Fig.3 Forming limit diagram of broken part
高强度钢板强度高,塑性低,板料流入量不足,是造成圆角破裂的根源。具体破裂原因是一方面,零件圆角部分与模具接触较早,温度降低过快,从图2(a)可以看出:温度越高板料高温软化越明显,变形抗力越低,塑性越高,所以圆角区域温降过快,塑性越低。另一方面,当板料受到压应力时可以阻碍晶间的变形[9],静水压力越大,晶间成形越困难,越有利于提高金属塑性越有利。从图3 可见:热冲压件的圆角区域受到双向的拉应力,致使塑性降低,进而在双向拉应力的作用下发生拉伸变形时厚度减薄过快发生破裂。同时图1 中汽车加强件B 和C 圆角处的拉深深度相对比较深容易进料不充分, A 处侧翻面的倾斜圆角使该区域的板料流动受阻更大,更不易于向B 处补充材料。所以,为了消除圆角区域的破裂现象必须改善该区域的温度降低过快和拉应力过大的现象。
图4 所示为成形结束后零件的厚度分布。从图4可知:圆角处的最小壁厚为1.234 mm,计算所得减薄率为31.45%。对于该类厚度的板料成形,若壁厚减薄率超过30%时,则制件很易出现破裂[10-11]。为解决圆角的破裂问题,拟对板料温度、摩擦因数等工艺参数进行优化。

图4 成形结束后零件的厚度分布Fig.4 Thickness distribution of part after formation
3 避免圆角破裂的优化设计
3.1 试验方案及目标值
以板料温度、压边力、摩擦因数为影响因子,进行三因子四水平的正交试验设计,板料温度x1的各水平为500,700,850 和1 000 ℃,摩擦因数x2的各水平为0.1,0.15,0.2 和0.3,压边力x3的各水平为10,30,50 和70 MPa,共进行16 次模拟分析试验,试验方案及目标值如表3 所示。
3.2 试验结果分析
3.2.1 回归模型方程的建立和显著性检验
处理数据建立响应曲面模型,验证试验结果的显著性。对高强度钢板的圆角厚度减薄率进行回归分析,分析结果显示二次项显著,进行二次多元回归拟合,得到的目标值与因子之间的响应模型为
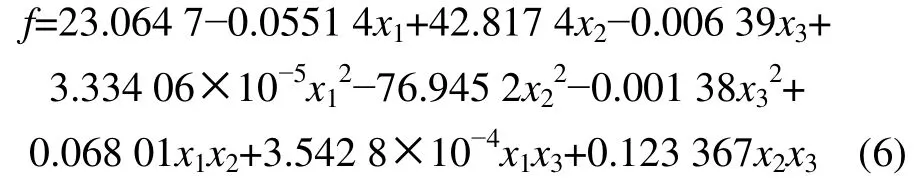
响应模型方程方差分析结果如表4 所示。从表4可见:F=25.11>F0.05(9,6)=4.10,P<0.05,表明响应模型极显著,不同处理间的差异极显著。模型的校正系数R2为0.974 1,证明该响应模型可以解释97.41%的因子与目标值之间的变化规律,仅有2.59%的数据不能用该响应模型进行解释。调整系数Radj=93.53%,S=2.301 12,说明实际值与预测值之间的误差比较小,模型的拟合程度较好,试验误差小,精度高。该模型可用于分析和预测板料厚度减薄率。利用式(6)预测的目标值见表3 中的f预测值。

表3 试验方案及结果Table 3 Experimental program and results
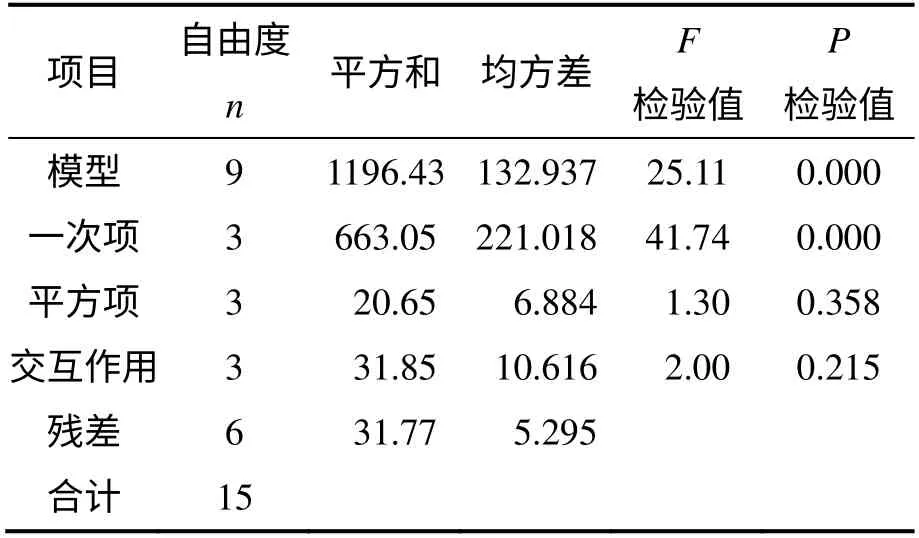
表4 回归方程的方差分析结果Table 4 Variance analysis of regression equation
3.2.2 响应曲面分析与优化
利用式(6)绘制的板料厚度减薄率响应曲面及等高线如图5~7 所示。从图5 可以看出:当温度在500~1 000 ℃之间,摩擦因数在0.1~0.3 之间时,随着温度的增加,响应值先减小后增大,随着摩擦因数的增加响应值一直增加。当温度在750 ℃左右,摩擦因数在0.15 左右时,响应值在10%~20%之间。从图6 可以看出:随着压边力的增加响应值不断增加,当压边力在30 MPa 左右时,响应值在10%~15%之间。从图7 可以看出:当响应值没有明显的波谷,但是从等高线可以进一步看出当压边力大致在35 MPa 之内,摩擦因数大致在0.17 之内时,响应值在20%之内。
通过响应曲面法对板料温度、摩擦因数、压边力进行单目标(板料厚度减薄率控制在30%之内)优化,对于如图1 所示的零件,最佳的工艺参数组合是:板料温度为850 ℃、摩擦因数为0.12,压边力为23.74 MPa,此时的板料厚度减薄率预测值为17.83%。
4 优化结果验证
4.1 仿真验证
采用优化结果进行模拟分析,得到如图8 所示的成形极限图,与优化前的结果(图3)比较得出汽车加强件的成形质量较好,圆角破裂现象得到了明显的改善,只有零件表面有少量的起皱现象,可以通过后续的整形工序进行校正,并且工艺补充面处的起皱现象不影响零件的使用性能不需要考虑[12-13]。优化后汽车加强件的B 和C 出的最大减薄率分别为18.27%和19.0%,符合厚度减薄率<30%的工艺要求,没有破裂现象出现。模拟得到的目标值为18.64%与预测值17.83%相近,验证了响应曲面优化分析的可靠性。

图5 x3=0 时响应f 与因子x1,x2 的三维曲面图和等值线图Fig.5 3D surface graph and contour for objective response f as x1 and x2 variables at x3=0

图6 x2=0 时响应f 与因子x1,x3 的三维曲面图和等值线图Fig.6 3D surface graph and contour for objective response f as x1 and x3 variables at x2=0

图7 x1=0 时响应f 与因子x2,x3 的三维曲面图和等值线图Fig.7 3D surface graph and contour for objective response f as x2 and x3 variables at x1=0
4.2 生产验证
依据优化结果进行生产试制,得到如图9 所示的成形件。从图9 可以看出:试验得到的零件成形质量比较好,在修剪线内没有出现明显的起皱、破裂等缺陷。通过拉伸试验和硬度测定,得出零件B 和C 两圆角的抗拉强度分别为1 380.20 MPa 和1 356.08 MPa,硬度分别为412.00 和401.94,均达到较高的强度和硬度,并且得到均匀马氏体组织,结果如图10 所示。可以满足生产要求[14-15],因而说明本文提出的将响应曲面法和数值模拟分析相结合的方法可以指导实际生产。

图8 优化后汽车加强件的成形极限图Fig.8 FLD diagram of optimized reinforcement

图9 优化后的成形件Fig.9 Forming parts after optimization

图10 圆角处的光学显微组织Fig.10 Optical microstructures of fillets
5 结论
1) 基于响应曲面法构建的函数模型符合度高达97.41%,与模拟结果的误差在5%之内,可以利用该模型代替数值模拟进行工艺参数优化。
2) 优化得到的最佳工艺参数组合如下:板料温度为850 ℃、摩擦因数为0.12、压边力为23.74 MPa。优化后的数值模拟和生产验证都得到了成形质量比较好的零件,圆角区域的抗拉强度和硬度都比较高,微观组织比较均匀,满足生产要求,表明提出的优化方法的可靠性,可指导高强度钢板的热冲压成形的试模和生产。
[1] Skår T, Krantz F. Wear and frictional behaviour of high strength steel in stamping monitored by acoustic emission technique[J].Wear, 2003, 255:1471-1479.
[2] Drillet P, Grigorieva R, Leuillier G, et al. Study of cracks propagation inside the steel on press hardened steel zinc based coatings[J]. La Metallurgia Italiana, 2012(1): 3-8.
[3] 张志强. 高强度钢板热冲压技术及数值模拟[J]. 热加工工艺,2010, 39(11): 103-105.ZHANG Zhiqiang. Hot stamping of high strength steel sheet and its numerical simulation[J]. Hot Working Technology, 2010,39(11): 103-105.
[4] 陈文琳, 邹文超, 曹俊. 基于响应面法的板料成形工作模面几何参数优化[J]. 农业机械学报, 2009, 40(11): 236-239.CHEN Wenlin, ZOU Wenchao, CAO Jun. Die-face-geometric parameters optimization based on response surface method[J].Transactions of the Chinese Society for Agricultural Machinery,2009, 40(11): 236-239.
[5] 张峻, 柯映林. 序列响应面方法在覆盖件成形过程优化中的应用研究[J]. 汽车工程, 2005, 27(2): 246-150.ZHANG Jun, KE Yinglin. A research on the optimization of auto panel forming process with sequential response surface method[J]. Automotive Engineering, 2005, 27(2): 246-150.
[6] SONG Guohui, WU Yu, LI Congxin. Engineering design optimization based on intelligent response surface methodology[J]. J Shanghai Jiaotong Univ, 2008, 13(3):285-290.
[7] LIU Hongsheng, BAO Jun, XING Zhongwen, et al. Modeling and FE simulation of quenchable high strength steels sheet metal hot forming process[J]. Journal of Materials Engineering and Performance, 2011, 20(6): 894-902.
[8] LIU Hongsheng, LIU Wei, BAO Jun, et al. Numerical and experimental investigation into hot forming of ultra high strength steel sheet[J]. Journal of Materials Engineering and Performance,2011, 20(1): 1-10.
[9] 朱巧红. 热成形模具热平衡分析及冷却系统设计优化[D]. 上海: 同济大学机械工程学院, 2007: 47-60.ZHU Qiaohong. Heat balance analysis of hot stamping and optimizing design of cooling system[D]. Shanghai: Tongji University. College of Mechanical Engineering, 2007: 47-60.
[10] 陈龙, 黄璞, 王炯, 等. 基于正交试验和灰色系统理论的拼焊板前纵梁成形优化[J]. 塑性工程学报, 2012, 19(4): 1-5.CHEN Long, HUANG Pu, WANG Jiong. Optimization of tailor-welded front longitudinal forming based on orthogonal experiment and grey system theory[J]. Journal of Plasticity Engineering, 2012, 19(4): 1-5.
[11] Marretta L, Lorenzo R D. Influence of material properties variability on springback and thinning in sheet stamping processes: A stochastic analysis[J]. International Journal of Advanced Manufacturing Technology, 2010, 51(1): 117-134.
[12] LIU Hongsheng, XING Zhongwen, BAO Jun, et al.Investigation of the hot-stamping process for advanced high-strength steel sheet by numerical simulation[J]. Journal of Materials Engineering and Performance, 2010, 19(3): 325-334.
[13] JIANG Chao, SHAN Zhongde, ZHUANG Bailiang, et al. Hot stamping die design for vehicle door beams using ultra-high strength steel[J]. International Journal of Precision Engineering and Manufacturing, 2012, 13(7): 1101-1106.
[14] CUI Junjia, LEI Chengxi, XING Zhongwen, et al. Predictions of the mechanical properties and microstructure evolution of high strength steel in hot stamping[J]. Journal of Materials Engineering and Performance, 2012, 21(11): 2244-2254.
[15] LIU Hongsheng, XING Zhongwen, LEI Chengxi. Hot formation quality of high strength steel BR1500HS for hot stamping without cooling system[J]. Trans Nonferrous Met Soc China,2012, 22(Suppl 2): 542-547.

