考虑履带滑动的转向过程仿真与试验验证

王红岩， 王钦龙， 芮 强， 盖江涛， 万 丽， 张 芳

(1. 装甲兵工程学院机械工程系，北京 100072； 2. 中国北方车辆研究所，北京 100072；3. 北京特种车辆研究所，北京 100072)

履带车辆的转向是决定其机动性能的关键因素之一，传统转向理论得出的结论无论在转向半径、转向角速度，还是在履带与地面之间的作用力等方面，与实际情况都有较大的差异[1]，其主要原因是没有考虑履带与地面之间的滑动。由于忽略了转向过程中履带的滑动，其结果是转向半径要比实际转向半径小约40%，理论转向阻力矩比实际值大50%以上[1-2]。最早研究考虑履带滑动的转向过程的是英国人W.Steeds[3]。前苏联学者对履带车辆转向性能进行了大量的研究[4]。日本的北野昌则[5]、加拿大的J.Y.Wong[6]等对履带车辆的转向过程做了大量的研究工作。国内在这方面的研究工作主要是从20世纪80年代开始的[2,7]。基于以上研究，本文建立了考虑履带滑动条件下的转向模型，并进行了实车试验验证，研究结果表明所建立的转向模型是可信的，可以用于实际工程中的转向参数修正性计算，具有一定的工程应用价值。

1 履带接地压力计算模型

图1为履带车辆转向过程的运动关系及接地压力。设大地坐标系为XOY，车体上的局部坐标系为xoy，车辆的几何中心为坐标原点，CG为车辆质心。

图1 转向过程的运动关系及接地压力

为了便于分析，假设如下：

1) 履带车辆在水平硬地面上作匀速转向运动，履带与地面之间的剪切力与剪切位移相关；

2) 不计履带的沉陷以及履带板在侧向剪切产生的推土效应；

3) 不计履带宽度对履带上的牵引力与制动力的影响，履带不可拉伸；

4) 履带与地面之间的接地压力考虑成连续线性分布的形式。

转向过程的大部分情况是高速侧履带滑转、低速侧履带滑移，这使两侧履带的转向极发生横向偏移，履带的瞬时转向中心如图1中的O′、O″所示，A2、A1分别代表高、低速侧的履带接地段转向极的横向偏移量。

在转向过程中，当车辆的质心出现离心力时，转向极有纵向偏移D，两侧履带的接地压力发生改变，履带接地段的法向负荷为

(1)

两侧履带的接地压力为

(2)

式中：R为转向半径(m)；yi(i=1，2)为两侧履带接地段任意点的纵坐标。

2 履带的纵向力、横向力及转向力矩

2.1 履带与地面之间的剪切变形

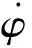
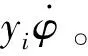
在大地坐标系下，两侧履带接地段上任意一点(xi，yi)的滑动速度在横向方向上的分量为

在纵向方向上的滑动速度分量为

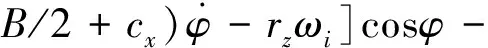
在两侧履带接地段上任意一点(xi，yi)，在XOY坐标系下，履带与地面之间的剪切变形量在X方向上的分量为

(cosφ-1)-yisinφ,i=1,2。

(3)

剪切变形量在Y方向上的分量为

sinφ-L/2+yicosφ,i=1,2。

(4)

履带接地段上任意一点(xi，yi)处的剪切变形为

(5)

2.2 履带的横向力与纵向力计算模型

当履带车辆在硬路面转向时，履带与地面之间的剪切作用力与两者之间的滑移量有关，剪切力可以表示为[7]

τ=pμ(1-e-j/K),

(6)

式中：p为履带与地面之间的正压力；K为土壤的剪切模量；μ为履带与地面之间的摩擦因数，为常量。

履带接地段单位面积上的切向作用力为

dFi=τidA=piμ(1-e-ji/K)dA,i=1,2。

(7)

两侧履带在纵向方向上的作用力为

μ(1-e-ji/K)sinδidy,i=1,2,

(8)

式中：δ1、δ2分别为高、低速侧履带滑动速度与x轴方向的夹角。

两侧履带在横向方向上的作用力为

μ(1-e-ji/K)cosδidy,i=1,2。

(9)

2.3 转向驱动力矩和转向阻力矩计算模型

根据两侧履带的纵向和横向方向的作用力，纵向力对图1中Ov点取矩，可以计算出转向驱动力矩，履带的横向力分别对两侧履带的O2、O1点取矩，可以计算出转向阻力矩。

两侧履带上的转向驱动力矩为

μ(1-e-ji/K)sinδidy,i=1,2。

(10)

两侧履带上的转向阻力矩为

μ(1-e-ji/K)cosδidy,i=1,2。

(11)

履带的滑移角δ1、δ2可根据图1中的运动学关系计算得出：

式中：Vjyi和Vjxi分别为两侧履带在局部坐标系的纵向方向和横向方向上的滑动速度。

2.4 转向的运动方程

根据履带作用力和转矩对局部坐标系的x轴、y轴方向力平衡，以及点Ov的力矩平衡关系，可以得到匀速转向运动方程为

(12)

(13)

(14)

式中：Rf1、Rf2为两侧履带的运动阻力，与两侧履带的法向负荷和道路阻力系数fr有关，即

(15)

在运动方程中，主要未知量是A2、A1和D，当给出车辆结构参数、地面参数以及转向运动学参数时，对以上3个方程进行迭代计算，可以得到各种车速和转向半径所对应的相对转向极偏移量a1、a2、a3，以及履带的作用力、转矩等。

2.5 转向运动学参数的修正系数

由于转向过程中履带的滑动，使得实际转向半径和转向角速度与理论值有较大的差别，为了在实际中准确估算转向参量的变化，需要给出转向半径和转向角速度的修正公式。

在局部坐标系，履带的瞬时转向中心点O′、O″在y轴方向上的速度是履带的理论速度，即

∓B/2+cx∓Ai)=Vi,i=1,2。

(16)

实际的转向角速度和相对转向半径为

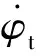
在转向过程中，由于履带与地面之间的滑动，实际的转向半径要比理论半径大，而实际转向角速度要比理论值小，即在一般情况下fρ>1，而fφ<1。

3 转向过程仿真与试验验证

3.1 履带滑动率的计算

计算中采用的行驶阻力系数由实车试验测试得到，变化范围为0.049～0.055，取f=0.05；履带与地面之间的摩擦因数μ=0.9；土壤的剪切模量K=0.015 m。

图2(a)、(b)分别给出了两侧履带的滑转率、滑移率随实际转向半径、车速的变化关系曲线。可见：两侧的滑动率都是随着转向半径的增大而减小；对于高速侧履带，车速对滑转率的影响较小；对于低速侧履带，当转向半径小于20 m时，车速对履带的滑移率略有影响。

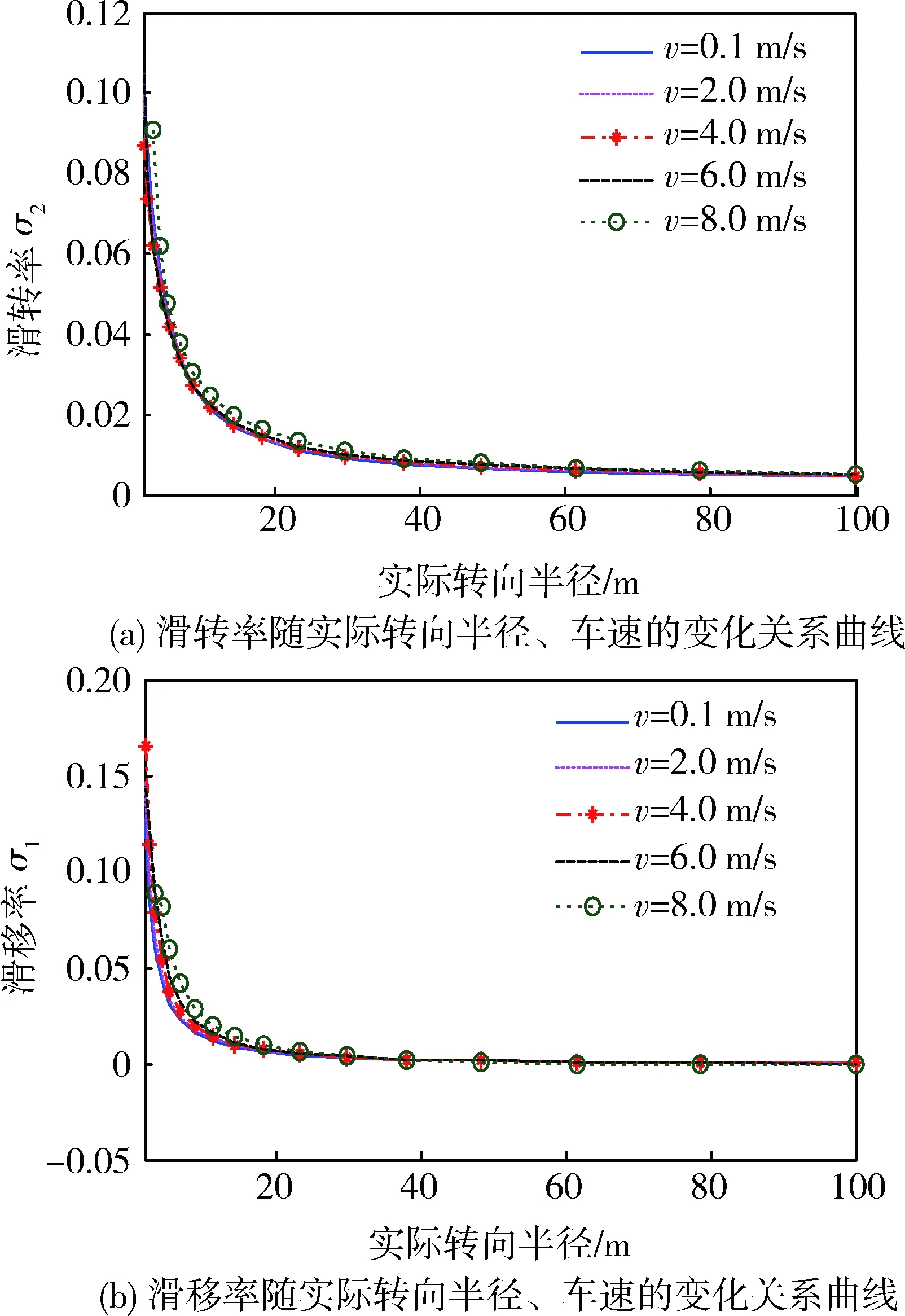
图2 履带滑动率随实际转向半径、车速的变化关系曲线

3.2 履带牵引力、制动力及转向阻力矩的计算

计算得到的两侧履带的牵引力、制动力如图3所示，图中给出了履带牵引力、制动力随车速和转向半径的变化规律，可以看出：两者都是随着转向半径的增大而减小的。由于离心力起到有利于转向的作用，因此，车速较高时，履带的牵引力、制动力要比低速时小。在较小半径范围内，离心力的影响更明显，特别是对低速侧履带的制动力的影响。

图3 牵引力、制动力随转向半径和车速的变化关系曲线

图4给出了转向阻力矩随转向半径和速度的变化关系曲线。可见：随着转向半径的增大，转向阻力矩减小；在转向半径较小情况下，车速对转向阻力矩的影响较明显。

图4 转向阻力矩随转向半径、车速的变化关系曲线

3.3 转向模型的试验验证

为了验证所建转向模型的可信性，笔者进行了实车试验，试验场地为沙土硬地面。试验时,履带车辆变速器挂1挡，工作在液力工况，车辆按顺时针方向连续进行不同半径下的转向试验。试验中同步记录车辆两侧主动轮转速、传动装置输出轴的转速和转矩、车辆的航向角、行驶轨迹、车速等信号。试验测试系统及传感器组成如图5所示。其中，车辆的转向半径、车速以及航向角等参数是由具有二次差分功能、高精度的GPS系统测取的。图6给出了GPS系统测试的车辆运行轨迹所拟合的转向半径图。

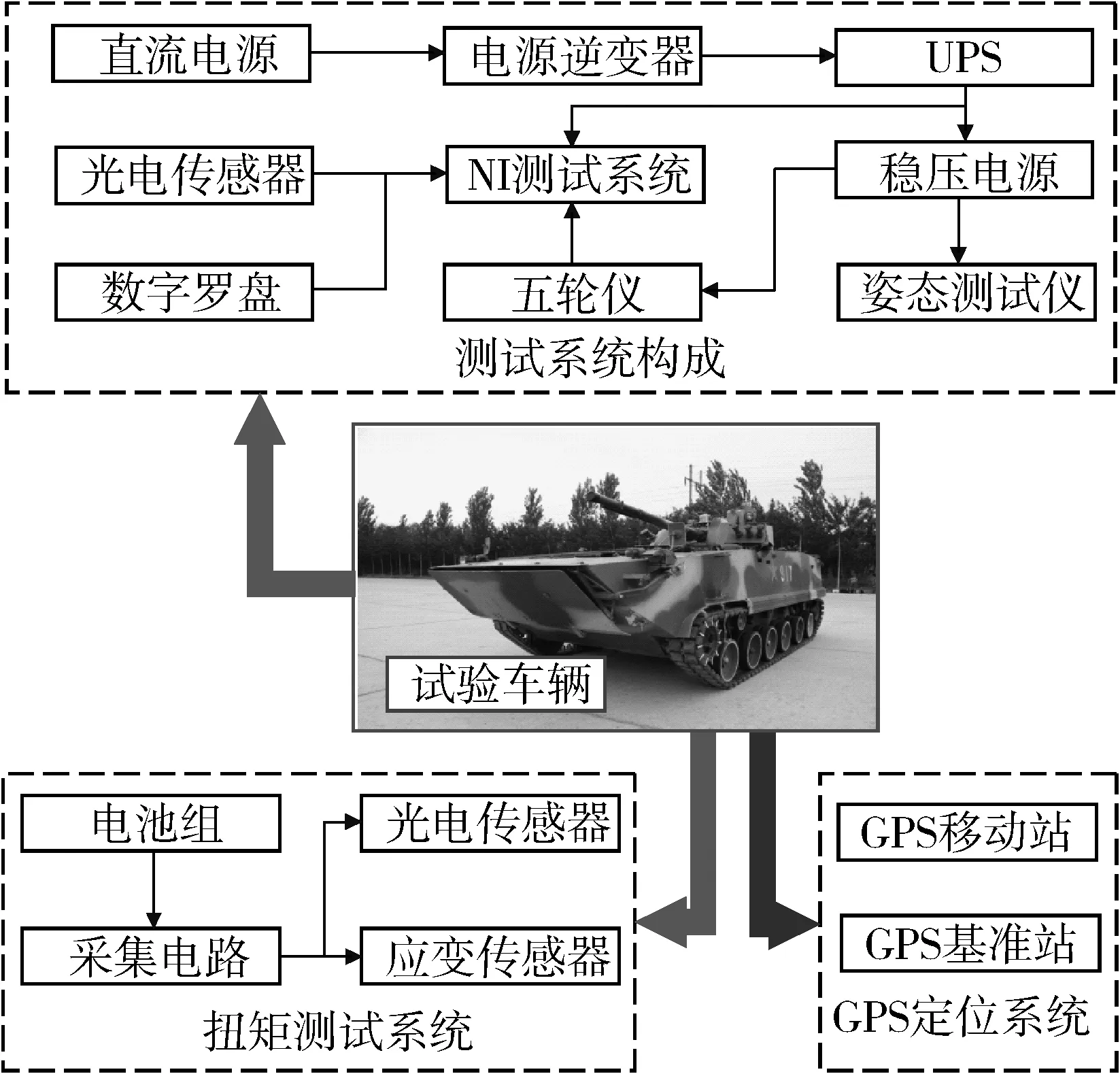
图5 试验测试系统及传感器组成

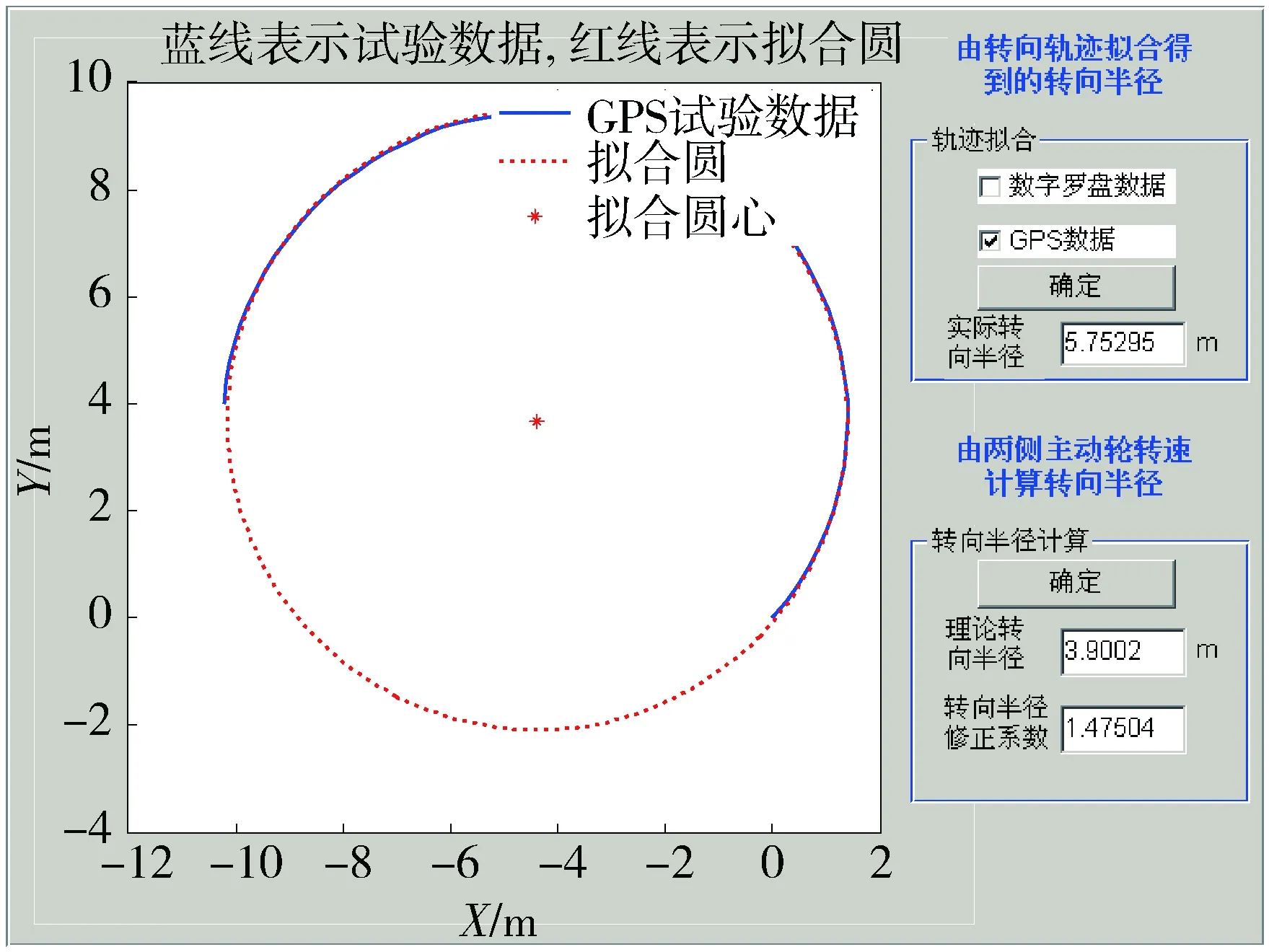
图6 转向轨迹拟合的转向半径

图7-9分别给出了转向半径修正系数、转向角速度修正系数、履带滑动率的计算与试验结果的对比。由图7、8可见：由于履带的滑动，实际的转向半径是理论转向半径的1.5倍左右；履带的滑动使转向角速度有所减小，是理论转向角速度的65%左右；各个半径下的转向半径、转向角速度修正系数的计算结果与试验结果具有良好的一致性。

图7 转向半径修正系数的计算与试验结果对比

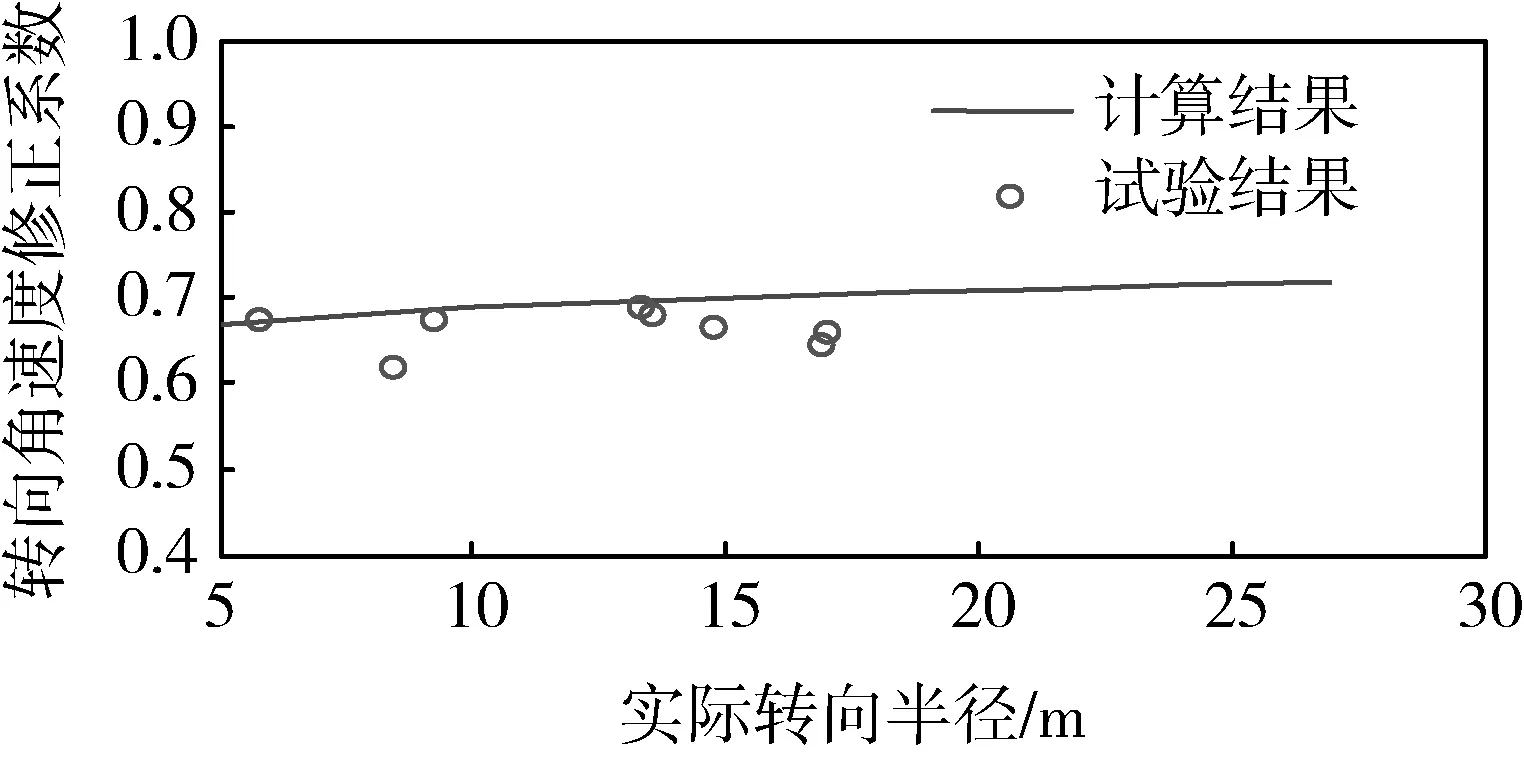
图8 转向角速度修正系数的计算与试验结果对比

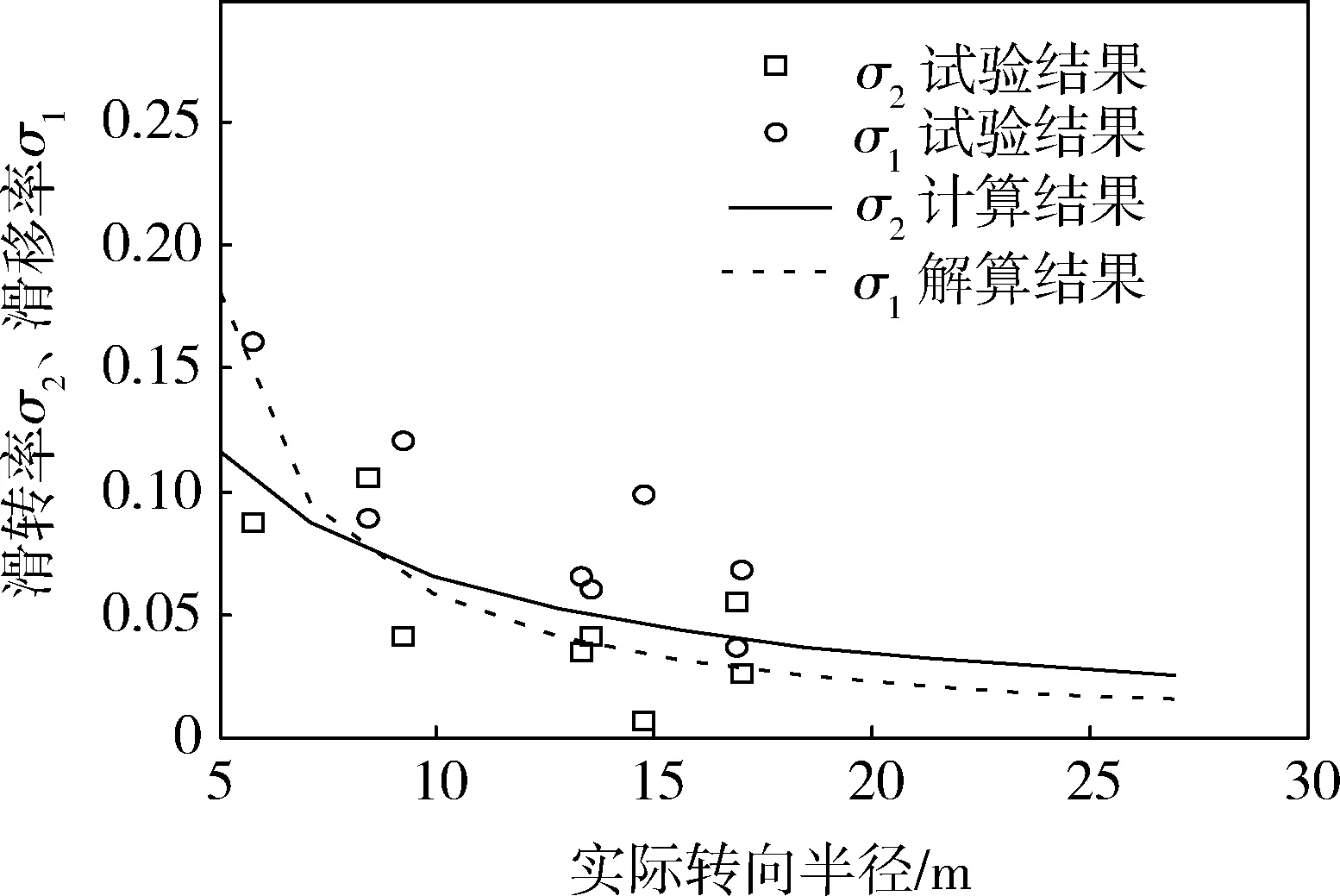
图9 履带滑动率的计算与试验结果对比

由图9可见：两侧履带的滑转率、滑移率的试验结果的分布范围较宽，但是试验结果与计算结果的变化趋势是一致的。

试验时，车速在0.665～1.025 m/s范围内变化，通过对转向轨迹的测量结果的拟合，获得一组转向半径，对应不同转向半径的履带牵引力、制动力的试验结果如图10中各点所示。图中的计算车速为1.0 m/s，从试验结果与计算结果的对比来看，两者的变化趋势和量值一致度均较高。

图10 履带牵引力、制动力的试验与计算结果对比

参考文献：

[1] 程军伟，高连华，王红岩．基于打滑条件下的履带车辆转向分析[J]．机械工程学报，2006，42(增刊)：192-195．

[2] 程军伟，高连华，王红岩，等．履带车辆转向分析[J]．兵工学报， 2007，28(9)：1110-1115．

[3] Steeds W．Tracked Vehicles：an Analysis of the Factors Involved in Steering[J]．Automobile Engineer，1950，4：143-148．

[4] 汪明德，赵毓芹，祝嘉光．坦克行驶原理[M]．北京：国防工业出版社，1983：29-35．

[5] Kitano M，Jyorzaki H．A Theoretical Analysis of Steerability of Tracked Vehicles[J]．Journal of Terramechanics，1976，13(4)：241-258．

[6] Wong J Y．Theory of Ground Vehicles [M]．3rd Edition．New York：John Wiley & Sons Inc，2001：390-420．

[7] 宋海军，李军，安钢，等．履带车辆转向过程仿真与试验研究[J]．装甲兵工程学院学报，2005，19(3)：17-21．