离散傅里叶变换在异步电机参数辨识中的应用

任志斌，曾 彪，曾德墙

（江西理工大学电气工程与自动化学院，江西赣州341000）

0 引言

在按转子磁场定向的异步电机矢量控制系统中，转子磁场能否准确定向取决于电机参数的准确性，进而影响系统的调速性能［1］。要对参数未测定的异步电机进行矢量控制时，准确辨识出电机参数，则是其控制系统具有良好调速性能的重要保证。在线辨识方法和离线辨识方法是目前异步电机参数辨识的两种方法。在线辨识包括遗传算法、粒子群算法等方法［2－9］，控制方法复杂，或者要增加一些额外设备，不易实现，目前尚处于理论研究和仿真阶段。传统的参数测试是利用堵转实验及空载实验来实现。但堵转操作不便，存在安全隐患，且实验中往往要电流表、电压表等测试设备，使这种方法有很大的局限性。该文研究了基于离散傅里叶变换（DFT）的异步电机离线辨识方案，易于实现，算法简单，且辨识精度高。

1 最小二乘法在辨识实验中的应用

最小二乘法是一种利用最小化误差的平方和来获取一组数据的最佳函数匹配的数据优化处理方法［10］。在直流实验中，电压与电流之间存在y＝ax＋b的线性关系，其中，y为相电压，x为相电流，a为电阻，b为此线性函数的参数。由于电压和电流在测量过程中存在误差，导致计算出的电阻不准确。实验中采取的是同一条件下多次测量方法，以便利用抵偿性来减少测量误差的影响。测出若干组xi，yi（i＝1，2，…，n）值，按最小二乘法的原理，未知参数a、b应该是

为最小值。使式（1）取极小值条件［11］为：

整理式（2）得：

解方程得：

其中，

因此，把所测数据代入式（5）就可以确定a，b的值了。

用最小二乘法处理数据，相对误差小，结果精确。采用最小二乘法处理数据是解决工程问题的一种非常有效、实用的方法。

2 离散傅里叶算法在辨识实验中的应用

设电压、电流含有k次谐波，则可用傅里叶级数表示为［12］：

其中，ak和bk分别是为各次谐波余弦相幅值和正弦相幅值：

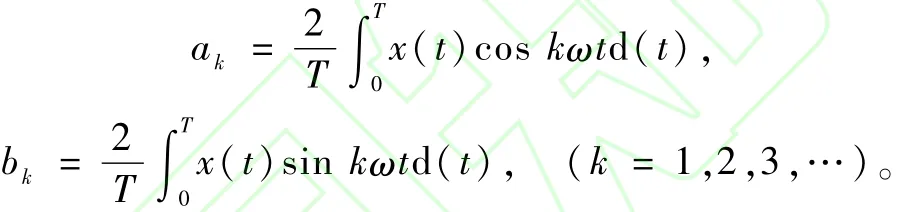
假设最高谐波次数为M，在每个周期内，通过均匀同步采样N个点获得序列x（n），如果要对序列x（n）作傅里叶变换，只要使周期采样次数满足N≥2M＋1［13］。

用离散序列表示为：

由式（11）可知，k次谐波的实部和虚部系数分别为：

电压、电流信号为连续信号，在实际计算中通过基波周期内同步采样进行离散化处理，设对电压、电流信号进行N次采样，则分别获得了电压、电流序列｛u（n）｝与｛i（n）｝，然后经过DFT变换，计算得到的电压电流基波成分为：

设电压、电流基波分量幅值为U1、I1，相位为θv、θi，则有：

功率因数角：

各次谐波的参数值可由离散傅里叶算法计算获得，然后利用各谐波分量就能间接求得总的电参数。这种方法滤波能力强，因此省去了硬件滤波装置，大大降低了成本，且能够起到减少系统误差的作用，适合于进行电压、电流信号分析。

3 参数辨识实验分析

电压空间矢量（SVPWM）是近些年发展的优化脉冲宽度调制（PWM）控制技术，按照特定的开关控制模式控制三相逆变桥，使得输出电流波形为正弦波形［14］。三相PWM逆变器原理图如图1所示。

图1 三相PWM逆变器原理图

3.1 直流斩波实验－定子电阻辨识

直流斩波实验中，将所产生的直流施加在异步电机定子上，由电感的特性可知：在直流电下电感相当于短路，回路中只有定子电阻Rs。等效电路如图2所示。

异步电机的定子电阻为：

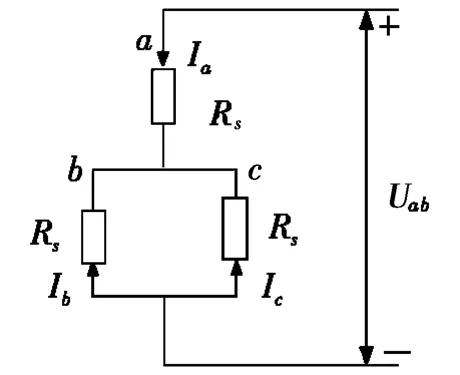
图2 直流斩波实验异步电机等效电路

控制逆变桥从而可以得到直流脉冲电压Uab，具体的实现流程为：令B、C相下桥臂恒通，对A相上桥臂金氧半场效应管（MOSFET）施加PWM脉冲，则调节PWM占空比，就能调节直流脉冲电压的大小。采用闭环控制来防止过流。利用逆变器三相开关管占空比和直流母线电压进行相电压重构［15］，那么线电压Uab也就可以通过相电压Ua得到了。相电流则通过电流传感器进行检测，由电流传感器的特性曲线，确定数字信号处理器（DSP）的模拟数字转换器（ADC）采样的相电流值与实际电流值之间的线性关系，从而获得实际的相电流值IA。采集电流和电压的若干组数据，利用最小二乘法对采集到的数据进行计算，进而得到定子电阻。

3.2 单相交流实验－转子电阻和漏感辨识

利用单相交流实验可以辨识出转子电阻、转子漏感和定子漏感。当只给异步电机定子的任意两相施加正弦交流电压时，由于不会产生电磁转矩，所以电机不会转动，类似于堵转。一般来说，定子漏感近似等于转子漏感，而互感Lm相对较大，故可忽略该回路的电流，相当于开路。等效电路如图3所示。

图3 单相实验异步电机等效电路

等效阻抗：

等效电阻：

等效电抗：

定、转子漏感：

式中，ω1为所加电压的基波角频率。

转子电阻：

在单相实验中，首先依据SVPWM算法，产生一单相交流电压，施加到异步电机定子侧。这一过程中，必须保证使B、C两相的导通状态始终一样。在不增加额外的硬件设备的条件下，同步采样电压、电流，通过离线计算，从而获得电压、电流的幅值及其功率因数角。

3.3 互感辨识－空载实验

互感辨识由空载实验来实现。通过逆变器产生旋转电压矢量Us，并施加到异步电机定子上，使其空载旋转。当空载运行时，异步电机没有带负载，转子转速几乎达到了同步转速，则转子支路近似开路。等效电路如图4所示。

图4 空载实验异步电机等效电路

等效阻抗：

等效电抗：

互感：

利用SVPWM算法，通过控制逆变桥产生圆形旋转磁场加在异步电机上，使电机旋转。在转速达到稳定状态后，类似于单相实验，采用离散傅里叶变换分析电压信号和电流信号，并通过获取其基波的实部、虚部，最后可计算出电压基波的有效值、电流基波的有效值及其功率因数。

4 参数辨识结果

采用TMS320F2812 DSP开发装置为硬件平台，并随意选取一台功率适当的异步电机，在此基础上进行辨识实验。异步电机铭牌为：额定功率40 W，额定电压24 V，额定电流4.2 A，额定频率50 Hz，额定转速1 400 rad／min。

在直流斩波实验中，待电流稳定后，通过数字模拟（DA）转换后，用示波器观察到直流电压和电流的波形，如图5a所示，直流斩波电压和电流保持不变。对电机的A相电压Ua和电流Ia进行连续采样，获取64组数据，利用最小二乘法进行计算，由式（16）可得定子电阻Rs。

图5 辨识实验中电压和电流波形

图5b为单相交流实验中电机的线电压和相电流波形，电压超前电流，电压和电流都近似于正弦波。图5c为空载实验中相电压和相电流波形，电压超前电流，相电流为正弦波，由于含有三次谐波，相电压为马鞍波。由实验波形可以明显看到电压、电流信号有较明显的干扰信号及谐波，因此采用离散傅里叶变换进行滤波和计算，能够消除谐波和干扰信号的影响，进而准确辨识参数。给定电流同步角频率ωe＝314.159 rad／s。电流、电压的采样周期为312.5μs，这样每采样64个数据恰好采样到一个周期20 ms的电流、电压。每隔312.5μs同时采样一次电流和电压，任取其中一个周期的数据，总共对64对数据进行DFT离散傅里叶变换，运用DFT计算线电压有效值Uab、相电压有效值Ua、相电流有效值Ia、功率因数cosφ和sinφ，根据式（17）～式（24）辨识定、转子漏感Llr＝Lls，转子电阻Rr及互感Lm。

表1 辨识实验结果

辨识结果如表1所示。

5 辨识参数的实验研究

利用离散傅里叶变换实现对异步电机矢量控制系统所需电机参数的辨识，其辨识结果为定子电阻Rs＝2.504 4Ω，定、转子漏感Llr＝Lls＝0.015 8 H，转子电阻Rr＝2.053 0Ω，互感Lm＝0.030 6 H。

将所辨识的电机参数在异步电机矢量控制系统中进行应用，以达到验证参数准确性的目的，其实验过程中相应波形如图6所示。

图6 矢量控制系统实验波形

在空载情况下，转速为600 r／min时，相电压、相电流、转速波形分别为图6a、图6b和图6c。相电压为马鞍波，相电流则逼近于正弦波，取得了较好的控制效果。图6c则为空载状态下转速的相应曲线，由图6c可以看出：转速无超调，且响应快，能够快速达到转速给定值，并保持稳定运行状态。图6d则是为从启动到突加负载过程中的相电流，在启动时，相电流增大，转矩也较大，待电机达到给定转速时，相电流有所降低，并维持稳定。在1.6 s时突加负载，可以观测到电流增大了，并快速建立了一个新的平衡，并维持稳定。由此可知，该控制方案的静态、动态调速特性好。实验表明了矢量控制系统定向准确，也就间接验证了所辨识电机参数具有较高的精度。

6 结论

通过将最小二乘法和傅里叶变换应用于电机参数的辨识，无需额外的硬件设备，具有实用性和简易性。所辨识的参数准确性高，是高性能矢量控制系统取得良好调速性能的基础，应用前景广阔。同时，必须说明的是，在电机运行过程中，由于受温度的影响，电机参数尤其是电机电阻会发生变化。异步电机参数在线辨识方法就是要实现在参数变化过程中进行实时校正，特别对于控制精度要求更高的矢量控制系统来说，显得尤为重要，也作为下一步研究的重点。

［1］ 孙大南，刘志刚，刁利军，等.牵引电机矢量控制转子磁场准确定向实时校正策略［J］.电工技术学报，2011，26（9）：116－123.

［2］ 徐奇伟，宋立伟，崔淑梅.感应电机矢量控制中转子参数自适应辨识［J］.电工技术学报，2011，26（6）：81－87.

［3］ 吴晓新，顾菊平，阮毅.基于自组织竞争网络的异步电机参数辨识研究［J］.微电机，2011，44（12）：21－24.

［4］ 郝桂芳，阴志先.强跟踪有限微分扩展卡尔曼滤波算法在异步电机中的应用［J］.太原理工大学学报，2011，42（6）：571－575.

［5］ 沈艳霞，陈中伟.高性能矢量控制中电机参数辨识及速度控制策略研究［J］.测控技术，2011，30（6）：67－71.

［6］ 李胜利.新型异步电机参数辨识方法［J］.煤矿机械，2012，33（8）：221－223.

［7］ 陈振锋，钟彦儒，李洁.感应电机参数辨识三种智能算法的比［J］.电机与控制学报，2010，14（11）：7－12.

［8］ 吴莹，黄显林，高晓智.一种文化鱼群算法及其在电机参数辨识中的应用［J］.电机与控制学报，2012，16（5）：102－108.

［9］ 才家刚.电机试验及性能分析简明手册［M］.北京：化学工业出版社，2013：236－240.

［10］ 王桂增，叶昊.主元分析与偏最小二乘法［M］.北京：清华大学出版社，2012：40－44.

［11］ 盘宏斌，罗安，唐杰，等.一种改进的基于最小二乘法的自适应谐波检测方法［J］.中国电机工程学报，2008，118（13）：144－150.

［12］ 冷建华.傅里叶变换［M］.北京：清华大学出版社，2004：200－202.

［13］ 吴静，金海彬.高准确度的相位差测量方法［J］.中国电机工程学报，2010，30（13）：41－45.

［14］ 康伟，张丽霞，康忠健.电流型双向PWM整流器SPWM与SVPWM控制输出特性比较［J］.电工技术学报，2011，26（11）：39－44.

［15］ 张旭，宋文祥，尹赟.一种三电平逆变器输出电压重构方法［J］.电气传动，2011，41（10）：29－32.