信息融合理论在消除多余力矩控制中的应用
赵书尚,冯清爽,叶秀玲,李阁强
(1.河南科技大学机电工程学院,河南洛阳471003;2.洛阳北方企业集团有限公司,河南洛阳471000)
0 引言
由于国防和民用工业的迫切需求,研制高性能的负载模拟器一直是飞行半实物仿真技术和加载技术的前沿课题[1-3]。早期负载模拟器的控制研究主要集中在多余力矩的控制方面,多采用结构不变原理,辅助同步补偿等方法。结构不变原理方法是设计一个前馈补偿器来达到有效抑制多余力矩的方法,但在实际应用中低频带效果尚可,高频带效果差;辅助同步补偿是利用位置补偿或速度补偿的办法来达到多余力矩的减小,但要做到舵机和负载模拟器的完全同步是不可能的,因此精度也不高。本文以信息融合理论为基础提出最优可预见控制算法。信息融合理论是研究相关信息、不相关信息、不确定信息、确定性信息及非线性信息的最优融合[4]。将最优预见跟踪控制器应用于被动式电液力伺服系中,通过仿真分析发现:最优预见跟踪控制器可以很好地抑制多余力矩的产生,达到更好的跟踪精度。
1 数学模型的建立
本文是以摆动马达作为控制对象建立的被动式电液力伺服系统。阀控摆动马达被动式电液力伺服系统的结构图如图1所示。图1中,左侧为加载系统,右侧为承载系统。加载系统和承载系统通过刚性连接轴连接在一起,加载系统的输出力矩受到了承载系统位置变化的影响,正是这种影响限制了被动式电液力伺服系统加载性能的提高。
阀控摆动马达被动式电液力伺服系统加载系统由以下方程来描述,式中物理量含义见文献[5-6]。
加载系统伺服阀的线性化方程:

加载摆动马达的流量连续性方程:


图1 被动式电液力伺服系统结构原理图
力矩平衡方程:

由方程(1)~方程(3)可以得到加载系统的开环传递函数为:

由式(4)中分子可以看出:承载系统的运动状态直接影响到加载马达的输出力矩,多余力矩的产生主要是由承载系统角位移的变化引起的。根据加载系统的传递函数得出加载系统的动力结构方块图如图2所示。
令干扰量为θl,伺服阀阀芯开口量XV=0,则输出量为T的传递函数为:

图2 加载系统动力结构方块图
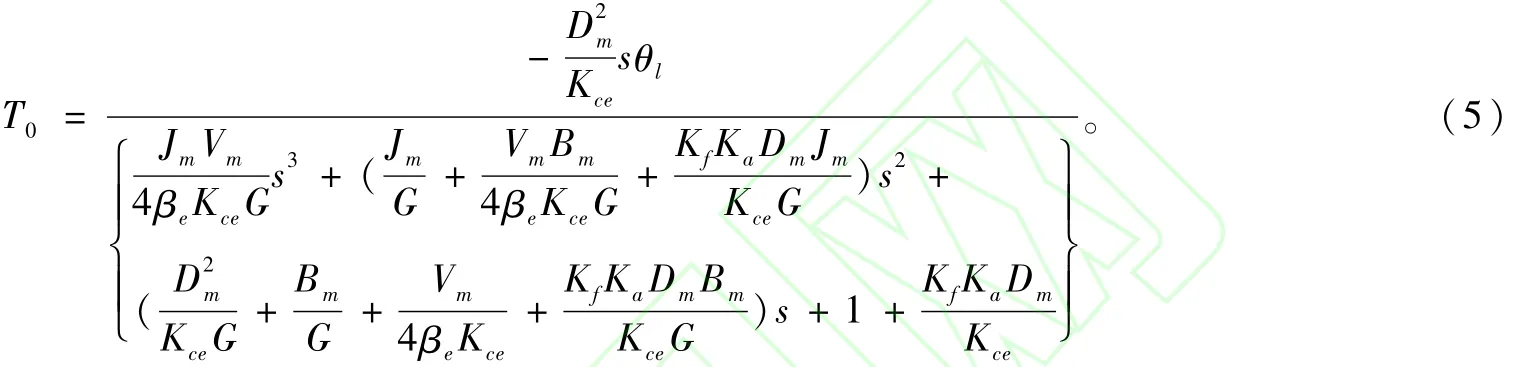
取仿真参数Jl=3.5×10-3kgm2,Gm=2.18×105Nm/rad,Bm=10 Nms/rad,Dm=8.14×10-5m3/rad,Jm=0.01 kgm2,βe=7×108N/m2,Vm=6.81×10-4m3,Ksv=2.52×10-2m3/(sA),令承载系统信号分别为θl=1°sin 2πt,θl=5°sin 2πt;θl=1°sin 2πt,θl=1°sin 10πt;比较承载系统在不同幅值信号或不同频率情况下对多余力矩的影响。代入仿真参数,得出仿真图形如图3所示。

图3 承载系统幅值及频率对多余力矩的影响
从图3可以看出:多余力矩在承载系统同频率不同幅值时会随着幅值的增加而增加;多余力矩在承载系统同幅值不同频率时会随着频率的增加而增加。另外,多余力矩的产生除了受到承载系统角位移变化的影响外,还受到承载系统角速度变化、角加速度变化的影响,其中角位移的变化是多余力矩产生的主要原因。
2 最优预见跟踪控制器的设计
在如何抑制多余力矩,提高系统跟踪精度方面,国内外学者进行了大量的研究。运用经典控制理论在一定程度上可以消除多余力矩、提高跟踪性能,但在小加载系统时并不能对系统起到有效的作用[7]。信息融合理论研究了不相关信息、相关信息、不确定信息、确定信息以及非线性信息的最优融合,将信息融合理论应用到控制问题中,把控制问题转化为估计问题,进而解决一些不容易解决的控制问题。根据信息融合的基本性质,信息融合常采用集中方式和序贯方式两种方法来进行求解。由于控制策略不同,序贯方式常用于闭环控制,集中方式常用于开环控制,对于被动式电液力伺服系统采用序贯方式来求解控制律。
假定控制对象为如下离散控制系统:

式中,x∈Rn×1是状态向量;y∈Rp×1是输出向量;u∈Rr×1是控制向量;A、B、C都为常数矩阵,维数分别为A:n×n;B:n×r;C:m×n。令B满秩,{A,B}可控。假定yr(k)表示输出向量,{u(k)}为求的最优控制序列,则二次性能指标为:
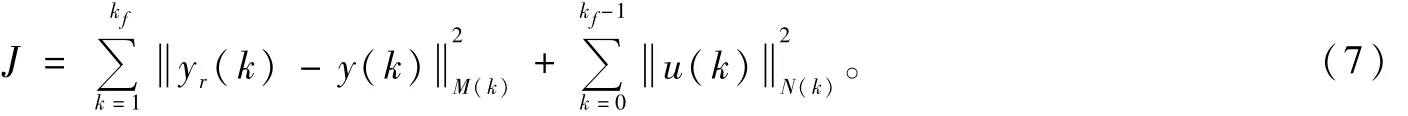
式(7)右边第1项约束了系统输出,这一项共提供了kf个输出信息,第2项约束了系统的控制量,表示控制量的消耗尽量小。假定在k时刻,xr(k+1)是yr(k+1)的最优估计,P(k+1)为信息量,则关于控制u(k)有如下方程表示:
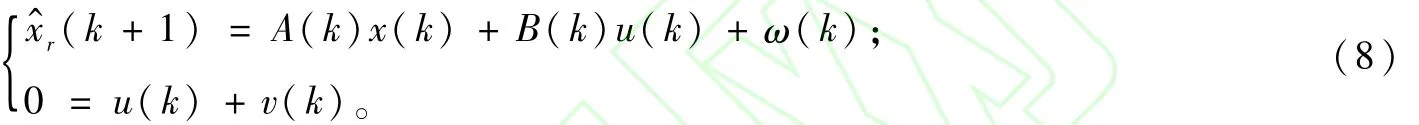
将式(8)变形并根据信息融合定理可以得到的最优融合信息量为:
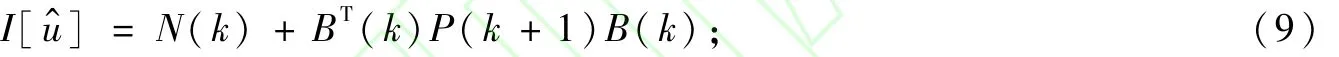
最优融合估计为:


式(11)中,v1(k)、v2(k)、v3(k)均为零值协方差,由信息融合理论得xr(k)的最优融合信息量为:
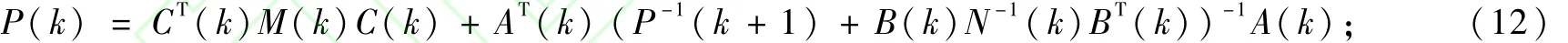
xr(k)的最优融合估计为:

以上是以信息融合理论为基础所设计的最优预见跟踪控制器的算法流程[8-10]。设计控制系统时,先设置初始参数,预测步长,输入给定信号,设置正定矩阵等,由式(12)~式(13)求出当前的融合信息量和虚拟状态值,最后求解当前k时刻控制律的融合估计u(k)。
3 仿真分析
由于被动式电液力伺服系实际的加载频率小于50 Hz,可以把伺服阀看作比例环节,考虑伺服放大器Ka=,则有Q=KsvKaUc。 引入式(1)~式(3)等可求得加载系统中各环节的传递函数方程如下:


式中,x= [ θmθmPL]T;u=Uc;d=θl;y=M;A=
被动式电液力伺服系统可以等效为多输入、单输出的系统,则可以把公式等效为:

式(15)对应的离散化方程为:

令加载信号为零,承载部分位移干扰信号幅值为1°,频率分别为5 Hz、10 Hz、15 Hz、20 Hz的正弦信号,正定权矩阵M=105、N=1、kf=20,取参数代入离散方程求得各系数,采用信息融合控制后,得到多余力矩仿真图,如图4所示。
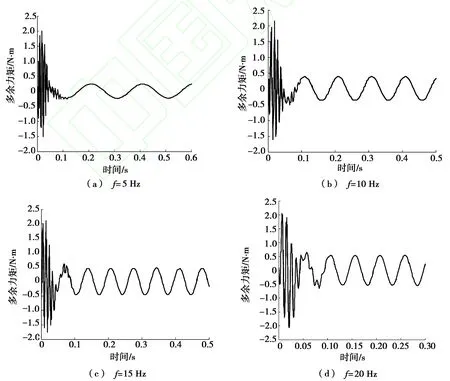
图4 信息融合控制力矩仿真图
由图4仿真结果可以看出系统在受到舵机干扰时多余力矩的情况。f=5 Hz时,多余力矩为0.30 Nm;f=10 Hz时,多余力矩为0.45 Nm;f=15 Hz时,多余力矩为0.49 Nm;f=20 Hz时,多余力矩为0.60 Nm。由此可知,采用信息融合控制理论很大程度上抑制了多余力矩的产生,同时说明了信息融合控制理论在消除多余力矩中的有效性。
4 结论
被动式电液力伺服系统是典型的非线性系统,具有很大的不确定性。采用传统的线性控制不能有效地消除多余力矩。在现代控制理论中,信息融合理论是研究不确定信息的一个常用的控制方法,可很大程度上消除系统本身不确定因素带来的影响。本文探讨了信息融合理论在消除多余力矩中的应用,给出了非线性融合控制算法并做出了仿真研究,验证了信息融合控制理论在消除多余力矩中的有效性。控制是一种策略,策略离不开信息,相信随着信息融合估计的发展,在融合不等式约束信息、时域指标信息等更一般的信息时,会更好地推动信息融合控制理论的发展。
[1] 李瑞,贾建芳,杨瑞峰.负载模拟器控制策略的研究综述[J].液压与气动,2012(10):12-16.
[2] 潘泉,增福,梁彦,等.信息融合理论的基本方法与进展[J].制理论与应用,2012,29(10):30-34.
[3] 李阁强,李水聪,黄飞.阀控非对称缸被动式电液力伺服系统的解耦控制研究[J].机床与液压,2013,41(1):7-10.
[4] 徐向荣.提高电液负载模拟器性能的研究[D].哈尔滨:哈尔滨工业大学,2006.
[5] 延皓,李长春,陈策.电液伺服系统综合负载模拟器仿真与试验研究[J].液压与气动,2013(3):49-51.
[6] 李阁强,赵克定,袁锐波,等.μ理论在电液负载模拟器中的应用[J].航空学报,2007,28(1):228-233.
[7] 王志胜,王道波.含理想控制策略和期望轨道的最优控制[J].控制与决策,2006,21(1):100-103.
[8] 李均阁.多源信息融合及其应用[J].甘肃科技,2013(2):62-67.
[9] Jiao Z X,Gao J X,Qing H,et al.The Velocity Synchronizing Control on the Lectro-Hydraulic Load Simulator[J].Chinese Journal of Aeronautics,2004,17(1):39-46.
[10] Chen Y H.Design of Robust Controllers for Uncertain Dynamical Systems[J].IEEE Transactionson Automatic Control,1988,33(5):487-491.

