混合流态下高速动压滑动轴承热润滑性能
王迎佳,魏 涛,岑少起,秦东晨
(1.郑州大学机械工程学院,河南郑州450002;2.河南工程学院计算机学院,河南郑州451191)
0 引言
流体径向滑动轴承具有承载能力强、回转精度高、寿命长等突出优点,在航空航天和高速精密加工机床主轴支承系统等高速、超高速旋转机械上有着广泛应用。
高速轴承油膜内复杂的流态是决定轴承静、动态性能的重要因素。对于工业上实际应用的轴承,由于结构要求,在同一轴承油膜中雷诺数相差较大,导致层流和紊流很可能同时存在于同一轴承油膜中,即出现了两种流态的混合状态[1]。虽然从20世纪60年代以来,高速滑动轴承的润滑理论研究(包括层流理论和完全紊流理论)取得了突飞猛进的发展[2-4],各国学者对此进行了大量深入的研究[5-12]。但目前的轴承润滑研究中大多忽略雷诺数的变化而假定油膜处于单一流态下,即要么层流,要么紊流,并依据层流或紊流润滑理论来计算轴承静、动态特性。显然,这很可能与实际情况不符,计算出来的油膜特性也会存在误差。而作为转子支承系统中的关键部件,滑动轴承的承载能力、摩擦功耗以及温升情况是影响轴承润滑效果、运转精度、稳定性的重要因素。因此,准确判定轴承内油膜流态分布是正确分析轴承特性的重要前提。
本文以高速动压径向滑动轴承为研究对象,基于层流、紊流润滑理论,将雷诺方程、能量方程和温黏关系方程有机结合,从而推导出油膜中多流态共存时的控制方程组,建立了层流、紊流同时存在于同一轴承油膜时的滑动轴承静态特性二维模型;并基于差分法编程求解方程组,分析主轴转速、偏心率等参数对油膜雷诺数、压力、温度分布以及承载力、摩擦力等静态特性的影响,形成了混合流态下动压滑动轴承静态特性的分析方法。
1 流态判据、控制方程及边界条件
1.1 油膜流态判据
雷诺数Re用来表征黏性流体的流动特性,Re=Uρh/μ,其中,U、ρ、h、μ分别为润滑油的流动速度、密度、厚度和动力黏度。通过比较其与临界雷诺数Rec(Rec=41.1(r/c)0.5,其中,r为轴颈半径;c为半径间隙)的相对大小来判定流体的流态是层流还是紊流。当油膜实际雷诺数Re小于Rec时为层流;当Re大于或等于Rec时为紊流。
在某些工况下,主轴转速较高,楔形油膜厚度相差较大,而且随着润滑油温度的升高,油黏度持续变小,会使流体各点雷诺数是个变量。则流体内非常可能会出现这样的情况:某些区域内油膜雷诺数Re小于Rec,为层流,而某些区域内Re大于或等于Rec,出现了紊流,也即在油膜中出现了层流、紊流共存的混合流态。
1.2 雷诺方程
设润滑油为不可压缩牛顿流体,忽略惯性力影响。假设轴承运转过程中,轴颈轴线始终与轴承轴线平行,即油膜厚度h不随轴向坐标变化。则由文献[4]可知:可导出层流和紊流流态下的二维无量纲雷诺方程:
层流流态下,
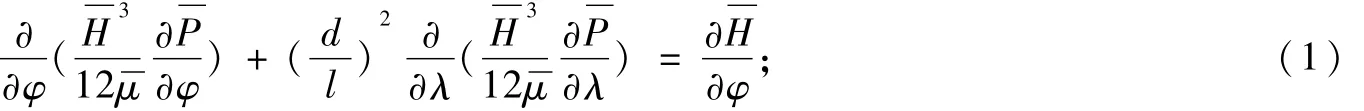
紊流流态下,
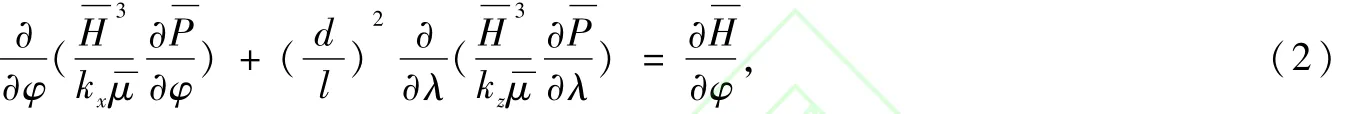
1.3 能量方程
本文对滑动轴承的热分析基于以下基本假设:(Ⅰ)绝热流动;(Ⅱ)润滑油在进油处的温度最低;(Ⅲ)润滑油密度和热容恒定不变,黏度只是温度的函数。引入T=T0,T、T0为润滑油温度和初始温度,可得到层流和紊流流态下二维无量纲能量方程如下:
层流流态下,

紊流流态下,

其中,A1=2μ0Ur/(ρcvT0c2),cv为润滑油比热;A2=A1/4。
1.4 温黏方程
黏度随温度的变化是润滑油十分重要的特性。常用的黏度与温度的关系式有Reynolds温黏关系式、Slotte温黏关系式、Vogel公式等,本文使用Reynolds温黏关系式,化为无量纲形式为:

大多数润滑油的动力黏度随温度的升高很快降低,而黏度直接影响雷诺数的大小,进而影响流态的判定。因此,在高速轴承润滑特性分析中,不能忽略温黏关系。
1.5 油膜厚度方程
图1为轴承结构示意图,如图1所示,由于轴颈轴线与轴承轴线平行,半径间隙c远小于轴颈半径r,则油膜厚度表达式为:

1.6 边界条件
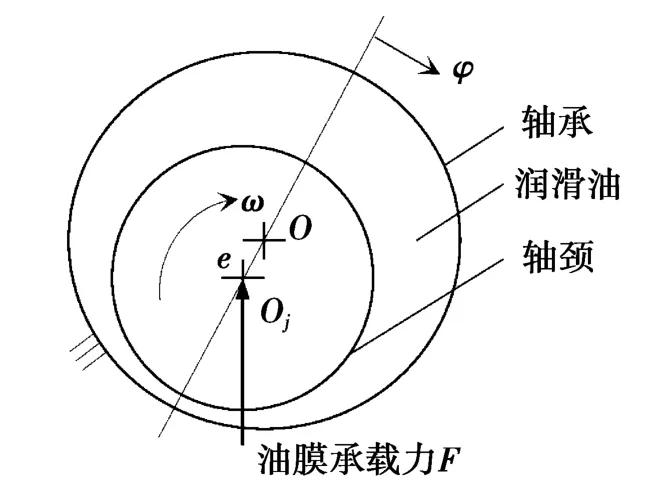
图1 轴承结构示意图
雷诺边界条件(亦可称为自然破裂边界条件)与实际测量结果比较接近,是应用更广而又比较合理的边界条件[4]。在进油边界上,即φ=0时,取为最大油膜间隙处,因动压滑动轴承中供油压力通常较小,可取压力为零,即=0;轴承两端边界和外界直接接触,压力也取为零;而油膜的终止边是油膜自然破裂的位置,位于最小油膜间隙之后发散区域内的某点,令此处φ=φt=0,且=0。本文采用雷诺边界条件,但油膜终止位置必须通过迭代计算得到,从而增加了求解的难度。
2 求解方法
本文采用有限差分法求解由前述控制方程所组成的方程组。图2为油膜差分网格划分示意图,如图2所示,将油膜划分为适当数量的网格,油膜周向用i编号,轴向用j编号,每个节点的位置用下标(i,j)二维编号表示。在周向共均匀划分为N格,i的编号就从1到(N+1),每一小格的宽度为△1= 2π/N;在轴向共均匀划分为M格,j的编号就从1到(M+1),每一小格的宽度为△2=2/M。则i,j即为节点(i,j)压力值i,j即为节点(i,j)温度值。

图2 油膜差分网格划分示意图
为节省篇幅,本文仅列出采用五点差分格式离散紊流流态下的雷诺方程的方法,层流流态下的雷诺方程和两种流态下的能量方程的离散方法基本相同,不再赘述。经系列推导,化简得紊流雷诺方程为:
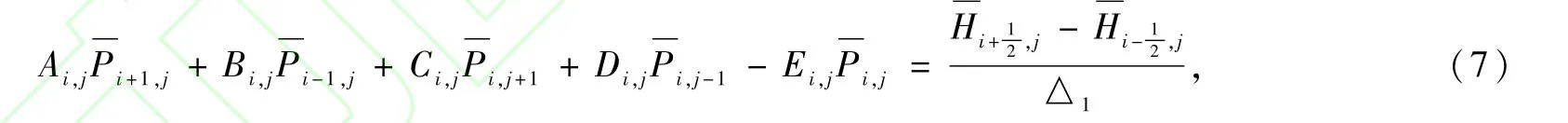
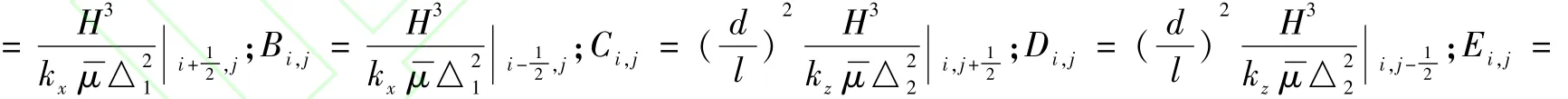
式(7)适用于所有内节点(i=2,…,N;j=2,…,M),所以各节点的式(7)构成(N-1)(M-1)个关于j的线性非齐次代数方程,由此方程组可以解出各内节点的压力值。
基于Matlab软件采用超松弛迭代法编程求解由离散后的雷诺方程、能量方程及计入温黏关系、边界条件所得到的控制方程组。先依据Reynolds边界条件将压力、温度和黏度初值赋予各边界节点,所有内节点压力取为零,作为首次迭代的初值;然后按照j=2,…,M的次序逐行计算,而每一行又按i=1,…,N逐点计算压力值。每算出一个压力新值,即取代该点的压力旧值。并将压力值为负数的节点压力值改为零。然后,将这些压力值代入能量方程以及温黏方程中求得各点温度、黏度的近似值,从而得到第2次迭代的近似结果。一直迭代下去,直至满足收敛条件,停止迭代,输出结果。
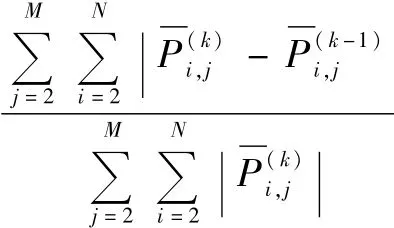
3 数值计算结果及分析
3.1 轴承的基本尺寸和计算参数
本文以普通圆柱动压径向滑动轴承为研究对象,轴承结构如图1所示。基本结构尺寸为:轴颈半径r=50 mm,半径间隙c=0.15 mm,宽径比l/d=1。润滑参数为:供油温度T0=40℃,温黏系数α=0.032 K-1,润滑油初始黏度μ0=0.038 4 Pas,密度ρ=860 kg/m3,热容cv=1 600 J/(kgK)。工作参数为:轴颈转速n=25 000 r/min,偏心率ε=0.1~0.8,临界雷诺数Rec=750。
3.2 雷诺数分布
图3a为不同偏心率条件下轴向中间平面内(λ=0)雷诺数沿周向的分布。由前所述,通过对比各点实际雷诺数和临界雷诺数的相对大小,可判断此处的流态。由图3a可见:各偏心率下油膜内基本处于层流、紊流共存的情况,特别在大偏心(ε=0.6~0.9)情况下,沿周向流态会发生多次转变。
由图3a可知:雷诺数曲线在某点附近数值非常接近,取其对应的周向角度为φz,则在区间[0,φz]内各点偏心率越小雷诺数越小,在区间[φz,φt]内各点偏心率越小雷诺数越大,大偏心时越过最小油膜厚度处后,黏度减小较多而使雷诺数快速增大。本工况下φz≈77.9°。
3.3 压力分布
图3b和图3c分别为不同偏心率下中间平面内沿周向的压力分布曲线和压力峰值所在轴向平面上的压力分布曲线。在各流态转换处,压力连续但压力梯度不连续,但由图3a可看出:雷诺数变化幅度不大,且油膜厚度连续,所以图3b和图3c中这种梯度不连续现象实际存在但并不明显。随偏心率的增大油膜压力峰值增大,如偏心率ε=0.8比ε=0.1时压力峰值高近21倍,压力峰值出现的位置处于油膜收敛区并逐渐向最小油膜厚度处移动。压力从零增大到峰值的过程中变化较为平缓,越过峰值后即迅速减小到零,这与楔形油膜压力的实际变化规律一致[4]。偏心率越大,油膜在越过最小油膜厚度处后越早破裂,油膜完整区域越小。由图3c可看出:沿轴向压力呈抛物线形分布,随偏心率的增大,轴承端部压力梯度逐渐增大。

图3 雷诺数、压力、温度和黏度沿轴向和周向的分布
3.4 油膜温度、黏度分布
图3d和图3e分别为不同偏心率下中间平面上沿周向各点温度分布曲线和φ=π处轴向平面上的温度分布曲线,图3 f为中间平面周向黏度分布曲线。由图3d~图3 f可以看出:相同条件下油膜沿周向温度逐渐升高,前半段各偏心下温升值比较接近,大约在20℃左右,而后半段偏心越大升温越快,如ε= 0.1时升温近12℃,ε=0.8时迅速升温近52℃;而温度沿轴向变化则平缓的多,中间平面温度稍低,接近轴承两端的位置温度稍高,但相差不大,如ε=0.8时,中间比两端温度低2.1%,即2.29℃,随着偏心率的减小,这种温度差异越来越小,当ε=0.1时温差为0.04℃。这说明油膜沿轴向温度变化与偏心率、主轴转速有关,但与绝对油温相比数值较小,在近似计算中也可认为温度沿轴向不变,这与文献[4]中的结论相似。沿圆周方向,黏度随温度的升高而持续减小,两者满足Reynolds温黏关系。小偏心时温升较低,黏度减小较少,而大偏心时温升较高,黏度减小也较多。
3.5 无量纲承载力和摩擦力
将前述求出的油膜压力进行相应积分,即可得到无量纲承载力和摩擦力。图4即为混合流态下油膜无量纲承载力和摩擦力随偏心率变化的曲线,并与无视实际流态变化而仅按单一层流和单一紊流计算的特性值[4]作对比。由图4可知:仅按单一层流和紊流计算的静态特性参数均和混合流态计算的结果有偏差。若按单一层流计算,承载力和摩擦力被低估最高可达15.3%和48.4%;若按单一紊流计算,承载力和摩擦力被高估最大可达28.2%和124.6%。由此可见,准确判断油膜内流态是正确得到轴承相应特性结果的重要前提。

图4 混合流态与单一流态下承载力、摩擦力的对比
4 结论
基于层流、紊流热流体润滑理论,采用有限差分法对处于混合流态下的高速动压滑动轴承进行了数值计算。通过改变偏心率得到油膜内雷诺数、压力、温度、黏度及承载力、摩擦力等静态特性参数变化曲线。研究结果表明:高速时油膜内流态变化复杂;仅按单一流态计算的静特性参数和实际情况差别较大。因此,流态的改变和热效应对高速轴承静态特性有着不可忽略的影响,在对轴承进行热流体润滑分析前,必须准确判定油膜流态分布,进而采用不同的润滑方程组,而且不能忽略温黏效应,才不会造成大的误差。
[1] 王迎佳,刘敏珊,岑少起,等.层流紊流共存时径向滑动轴承热流体润滑性能分析[J].郑州大学学报:工学版,2013,34(5):43-47.
[2] Ng CW,Pan C.A Linearized Turbulent Lubrication Theory[J].Journal of Basic Engineering,1965,87:675-688.
[3] Pinkus O,Sternlicht B.Theory of Hydrodynamic Lubrication[M].New York:McGraw-Hill Book Company,1961.
[4] 张直明,张言羊,谢友柏,等.滑动轴承的流体动力润滑理论[M].北京:高等教育出版社,1986.
[5] 胡伟奇,段明德,汪玉平,等.基于热流网络法的电主轴支撑系统热特性研究[J].河南科技大学学报:自然科学版,2013,34(2):17-21.
[6] Shyu S H,Li F,Jeng Y R,et al.THD Effects of Static Performance Characteristics of Infinitely Wide Turbulent Journal Bearings[J].Tribology Transactions,2010,53(6):948-956.
[7] Shyu SH,Lee W R,Hsieh S J,et al.Static Performance Characteristics of Finite-Width Turbulent Journal Bearings with THD Effect[J].Tribology Transactions,2012,55(3):302-312.
[8] Boubendir S,Larri S,Bennacer R.Numerical Study of the Thermo-hydrodynam ic Lubrication Phenomena in Porous Journal Bearings[J].Tribology International,2011,44(1):1-8.
[9] Santos E N,Blanco C JC,Macedo E N,et al.Integral Transform Solution for the Analysis of Hydrodynamic Lubrication of Journal Bearing[J].Tribology International,2012(52):161-169.
[10] Solghar A A,Gandjalikhan N S A.Numerical Analysis of Turbulent Lubrication in Plain Full Journal Bearing[J].Industrial Lubrication and Tribology,2013,65(2):91-99.
[11] 杨建玺,周浩兵,崔凤奎.液体动静压轴承油腔结构对承载特性的影响[J].河南科技大学学报:自然科学版,2012,33(5):37-40.
[12] 郑学普,周彦伟,邓四二,等.航空发动机主轴-轴承系统温度场分析[J].河南科技大学学报:自然科学版,2004,25(1):30-33.

