引入信道先验信息的卫星信道建模方法

郭业才，徐 冉，王南南

（南京信息工程大学a.电子与信息工程学院；b.江苏省气象探测与信息处理重点实验室；c.江苏省气象传感网技术工程中心，江苏南京210044）

0 引言

卫星通信系统中存在着非线性效应，这种非线性效应作用于通过卫星信道的信号，将会在接收端获得产生严重幅度畸变和相位旋转的信号。卫星内部高功率放大器（主要是行波管放大器）工作在饱和点或其附近是导致卫星信道非线性特性的原因之一，国内外对于卫星信道非线性特性的研究通常只考虑这一因素，具有一定的局限性［1－2］。文献［3］指出了非线性放大器和群时延效应都是导致信号非线性失真的重要原因，但是没有将两者联合加以研究。

采用合理的非线性模型去尽可能地逼近卫星信道的非线性特性，是对卫星信道非线性特性进行后续研究的关键。文献［4］推导了一种简化的非线性卫星信道VOLTTERA级数模型，文献［5］采用维纳模型对行波管放大器的非线性特性建模，两者均没有充分利用信道的先验信息，且没有研究群时延效应对卫星信道传输信号的影响；文献［6］提出采用ANFIS模型去辨识一个非线性系统，依据是ANFIS模型具有对非线性系统无限逼近的能力，但是也没有考虑信道的先验信息对非线性系统建模的影响。本文综合考虑了非线性放大器和群时延的非线性效应，构建了综合两种效应的卫星信道模型；在分析信道先验信息的基础上，构建了基于信道先验信息的卫星信道解析式模型。

1 卫星通信系统模型

非线性卫星信道等效基带模型如图1所示［7］。

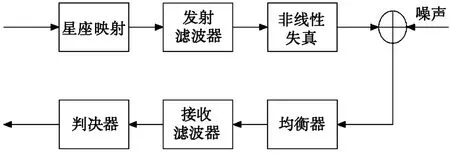
图1 卫星信道的等效基带模型

图1中的非线性信道表示综合行波管放大器非线性效应和群时延效应的联合信道。其中，行波管放大器的非线性效应与输入信号的瞬时功率有关［8］，而群时延效应与信号通过发射机、无线环境、卫星内部放大器所引起的相位的非线性变化有关，这两种非线性是相互独立的［3］，但是，由放大器中的线性滤波器和无线环境所产生的群时延信道会对输入放大器非线性部分信号的幅度产生影响，进而影响放大器非线性部分的调幅－调幅和调幅－调相效应。

基于上述分析可知：信号通过线性滤波器、非线性放大器及无线空间的组合信道和通过这个组合信道的群时延信道的过程是相互独立的，两个过程的输出信号相乘后产生整个系统的输出信号；信号通过由线性滤波器和无线环境所产生的群时延信道，与信号通过线性滤波器和无线环境的非群时延信道的过程是相互独立的，通过这两种失真效应的输出信号相乘后产生的信号共同作用于行波管放大器的非线性部分，控制行波管放大器的调幅－调幅和调幅－调相效应。

综合考虑卫星信道非线性效应产生的因素的同时，为了简化分析，将发射滤波器、上行链路无线环境与卫星内部高功率放大器的线性部分进行合并形成线性组合信道后，得到图2的卫星信道模型。

图2 卫星信道模型

图2中，a（n）为系统输入信号；b（n）为a（n）通过线性组合信道的输出信号；群时延信道1表示线性组合信道的群时延信道信道；z1（n）为a（n）通过群时延信道1的输出信号；x（n）为a（n）通过线性组合信道输出信号和a（n）通过群时延信道1输出信号的乘积除以a（n），是不可测量的；群时延信道2本应表示整个系统的群时延信道，为群时延信道1和非线性放大器群时延信道的级联，但是另一路a（n）在通过组合信道时已与线性组合信道的群时延效应进行了一次相乘，若再与整个系统的群时延效应相乘将会多乘一次线性滤波器的群时延效应，所以这里的群时延信道2应表示非线性放大器的群时延信道；z2（n）为a（n）通过群时延信道2的输出信号；y（n）为x（n）通过放大器调幅－调幅和调幅－调相非线性效应信道的输出信号；s（n）为整个系统的输出信号；TWT表示行波管放大器的非线性部分，具有调幅－调幅和调幅－调相效应，本文采用Salah模型的一种变形模型来描述这种非线性效应［9］，

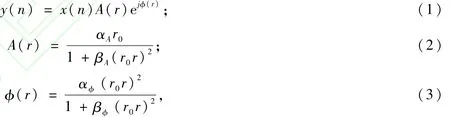
式中，A（r）和φ（r）表示卫星信道的调幅－调幅效应和调幅－调相效应；r＝，P（t）为输入信号的瞬时功率，为输入信号的平均功率；r0表示输入信号的幅度回退，dB；αA＝2.158 7；βA＝1.151 7；αφ＝4.003 3；βφ＝9.104 0。

进一步分析图2，信号通过线性滤波器、非线性放大器和群时延信道的实质都是使得输入信号产生了幅度畸变和相位旋转，有式（4）～式（9）。

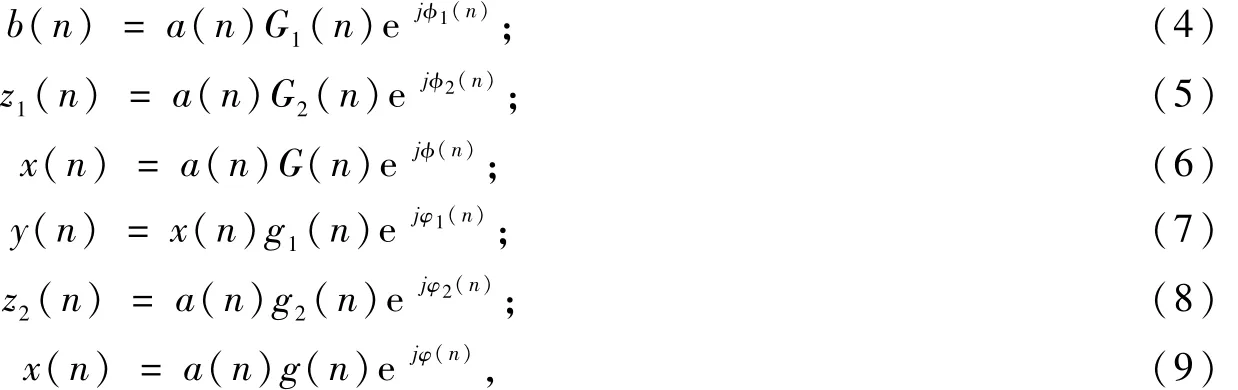
式中，G1（n）、G2（n）、G（n）分别为线性组合信道、群时延信道1以及行波管放大器之前信道的幅度增益；φ1（n）、φ2（n）、φ（n）分别为各个信道的相位变化；g1（n）、g2（n）、g（n）分别为非线性放大器调幅－调幅、调幅－调相非线性信道、群时延信道2以及整个系统的幅度增益；φ1（n）、φ2（n）、φ（n）为各个信道的相位变化。根据图2中各系统与其各自对应群时延信道的独立性，结果见式（10）～式（13）。

结合式（4）～式（9），得到如下关系：

由此，可以获得一条关于信道结构特性的先验信息。

2 基于信道先验信息的卫星信道建模

2.1 非线性卫星信道的先验信息

根据上节的分析所得到的卫星信道的先验信息有以下类型：

先验信息1：图2中的线性组合信道可以视为一个有记忆的线性滤波器。

先验信息2：群时延信道为非线性信道。

先验信息3：由式（14）和式（15）可知，将线性组合信道和群时延信道1看成是相互独立的两个滤波器，非线性放大器之前系统的输出为这两个滤波器输出信号乘积除以一次系统输入信号a（n）；将整个系统的非群时延信道和群时延信道2看成是相互独立的两个非线性滤波器，整个系统的输出为这两个滤波器输出信号乘积除以一次输入信号a（n）。

2.2 建模过程

本文所采用的建模方法与传统方法主要的不同在于：传统方法是直接采用特定的非线性函数（解析式模型）去逼近一个非线性卫星信道。而本文首先将现有信道结构解析式拆分成线性表达式和非线性表达式；然后，根据已知信道的先验信息，采用相应的线性和非线性表达式分别表示由先验信息推知的信道结构；再结合已知信道信息将各部分组合起来，完成信道模型的构建；最后，用新构建的解析式模型去逼近所研究的信道，完成信道建模过程。

以维纳模型为例，维纳模型的表达式为：

其中，W表示维纳模型的线性部分系数；F表示维纳模型的非线性部分系数；X（n）和Y（n）分别为线性和非线性部分的输出。本文采用维纳模型的线性和非线性部分表达式来构建新模型的线性和非线性部分。

设整个系统的输入信号为a（n），由先验信息1和先验信息3可知：输入信号首先通过一个有记忆的线性滤波器和其对应群时延滤波器的级联滤波器，用维纳模型的线性部分表达式表示线性组合信道，非线性表达式表示群时延滤波器，得到其输入－输入表达式为：

式中，c1m1（m1＝0，1，2，…，M1）为线性滤波器系数；c2m2（m2＝0，1，2，…，M2）为群时延滤波器系数。根据卫星内部行波管放大器的调幅－调幅和调幅－调相效应，再结合先验信息1，得到式（19）～式（22）。

式中，G（n）和p（n）分别表示非线性放大器的幅度和相位变化；c3m3（m3＝0，1，2，…，M3）为调幅－调幅效应表达式的权系数；c4m4（m4＝0，1，2，…，M4）为调幅－调相效应表达式的权系数；ρ（n）为x在n时刻的瞬时功率。由先验信息3，得整个系统的输出s（n）。

其中，c5m5（m5＝0，1，2，…，M5）为群时延信道2表达式的权系数。

根据先验信息2，除了知道群时延信道是非线性信道外，无法获得更多对解析式模型构造有帮助的信息。直接采用维纳模型的非线性部分表达式去表示群时延信道将带来一个问题：若群时延信道是一个复杂的有记忆非线性信道，这个有记忆非线性信道既具有记忆性且信道结构不能表示成有记忆线性结构和无记忆非线性结构的级联，则维纳模型的非线性部分将无法较好地表述这种非线性，若表示群时延的非线性模型在与实际信道逼近的过程中发散，将造成构建的整个解析式模型在逼近信道的过程中收敛性能下降甚至无法收敛，解决这个问题的方法是引入文献［10］所采用的一种非线性软判决函数：

这样，式（18）和式（23）可改写为：

软判决函数的功能就是控制其自变量函数的收敛，若本文所构建的群时延函数在逼近真实信道的过程中能够收敛，则维持其性能，若不能收敛，则限制其输出以维持整个模型的性能。

由式（18）～式（26），得到了基于信道先验信息、综合放大器非线性效应和群时延效应的非线性卫星信道解析式模型。

系统建模的过程其实就是采用相应的解析式对信道进行辨识的过程，设系统辨识的代价函数为：

其中，e（n）＝sout（n）－s（n），sout（n）为实际信道的输出。

系统辨识的过程就是利用随机梯度下降法不断地更新解析式模型各部分的权系数，以使得解析式模型输出尽可能地逼近信道输出，即让s（n）尽可能地逼近sout（n）。利用瞬时均方误差代替统计均方误差，并采用随机梯度下降法更新模型各部分权系数，权系数迭代式为：

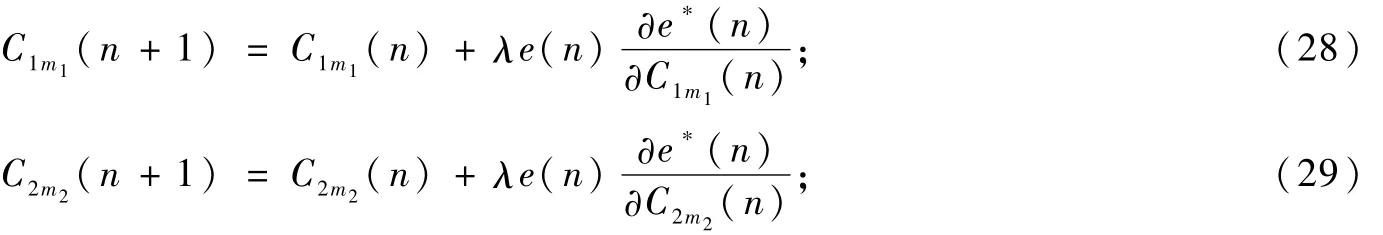
式中，C1m1＝｛c11，c12，…，c1M1｝；C2m2＝｛c21，c22，…，c2M2｝；C3m3＝｛c31，c32，…，c3M3｝；C4m4＝｛c41，c42，…，c4M4｝；C5m5＝｛c51，c52，…，c5M5｝分别为模型各部分的权系数。令

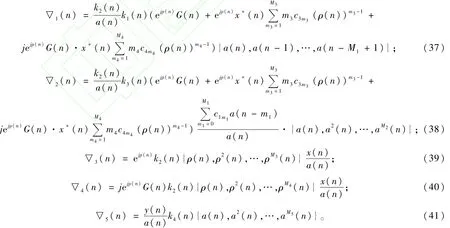
3 仿真结果

为了验证本文构建的解析式模型性能的优越性，采用8PSK信号作为模型的训练信号，线性组合信道参数取［0.796 2 0.153 8 0.076 9］［9－12］；图2中整个系统的群时延信道为文献［3］中设计的群延时信道，参数为：

h＝［0.009 1＋0.001 4j －0.024 7＋0.004 4j 0.054 9－0.005 6j －0.124 6－0.014 9j 0.238 1＋ 0.251 8j 0.707 9－0.468 8j 0.238 1＋0.251 8j －0.124 6－0.014 9j 0.054 9－0.005 6j －0.024 7＋0.004 4 j 0.009 1＋0.001 4j］；

整个系统的群时延信道为群时延信道1与群时延信道2的级联，假设这两个信道具有相同的信道参数。维纳模型、本文构建模型各部分权系数阶数均为3，抽头初始化均采用中心初始化法，维纳模型线性和非线性权系数迭代步长为0.000 8，本文构建模型各部分权系数迭代步长为0.000 5。

图3和图4分别为非线性放大器输入功率回退为较小和较大时两种模型逼近实际信道的均方误差曲线，每条曲线均进行了50次蒙特卡罗仿真获得，为了更好地观察曲线的收敛位置，还对每条曲线做了平滑处理；输入功率回退表示放大器工作在饱和点时的输入信号功率与实际输入信号功率的差值，这个差值越小，非线性放大器的调幅－调幅和调幅－调相效应越强，信号由非线性放大器调幅－调幅和调幅－调相效应所引起的非线性失真越严重。

从图3中可以看到：由于本文构建模型充分利用了信道的先验信息，使得模型结构从一开始较维纳模型与实际信道结构的拟合度就要高，所以在迭代初期，本文模型输出与实际信道输出的均方误差较维纳模型要小。在两种模型与实际信道不断逼近的过程中，相对于包含极少量信道信息的维纳模型，本文构建的模型由于包含了尽可能多的已知信道信息，迭代时模型参数只需做较小的调整就可匹配实际信道，所以收敛速度更快，图2中，本文模型的均方误差曲线在1 500步左右收敛，而维纳模型的均方误差曲线经历了大约4 800步才收敛，收敛后，本文构建模型的稳态均方误差也要略低于维纳模型。

图4表明：非线性放大器的非线性效应越弱，两种模型对信道的逼近程度越好，但是观察图3和图4中两种曲线收敛之后曲线之间的距离发现，随着放大器非线性效应的减弱，本文构建模型的性能提升较维纳模型更加明显。

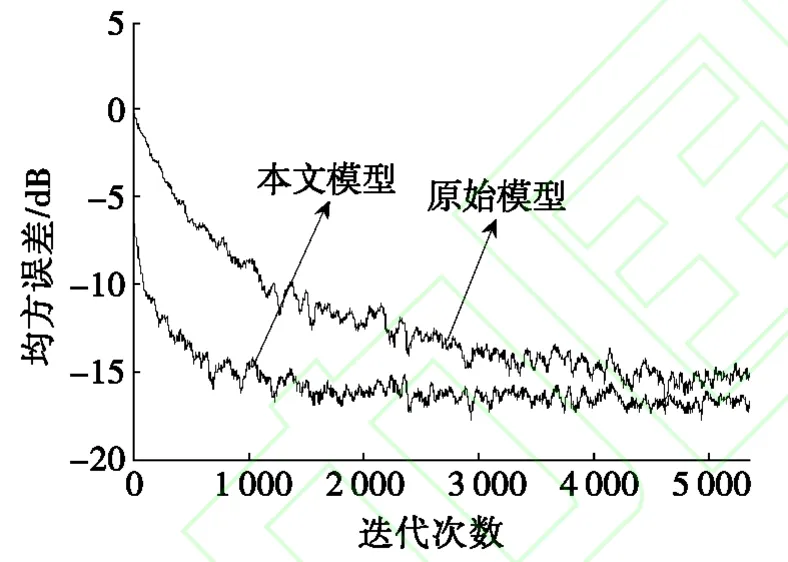
图3 输入功率回退较小时两种模型训练曲线

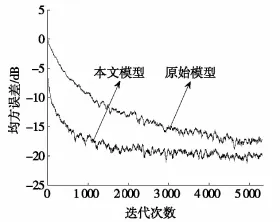
图4 输入功率回退较大时两种模型训练曲线

由于采用了维纳模型的线性和非线性部分结合信道先验信息对非线性卫星信道进行建模，本文构建的解析式模型的性能本身要受到维纳模型性能的影响，若选用其他对非线性信道逼近能力更强的非线性函数作为模型构建的工具函数，则可获得更好的效果。

4 结束语

本文分析了导致卫星信道非线性特性的非线性放大器的调幅－调幅、调幅－调相效应和群时延效应产生的原因与各自的特点，构建了一种综合两种非线性效应的卫星信道模型，更为精确地描述了卫星信道的非线性特征；同时，以维纳模型为工具，结合卫星信道的先验信息，构建了一种综合卫星信道非线性放大器的调幅－调幅、调幅－调相效应及群时延效应的信道解析式模型，采用随机梯度下降法对模型各部分权系数进行更新，并与维纳模型的建模效果进行了仿真对比。仿真结果表明：本文构建的模型在对信道进行逼近的过程中，无论在收敛速度还是稳态均方误差方面，性能都要好于维纳模型。

［1］ Thomas D，Gerhard B，Vito D.Transmit Precoding for M IMO-BI-CM-ID Satellite System with Nonlinear Power Amp lifiers［J］.Global International ITG Workshop on Smart Antennas，2013，3（11）：1639－1647.

［2］ 崔霞霞，张俊祥，潘申富.非线性卫星信道均衡［J］.无线电工程，2004，34（10）：49－51.

［3］ 张晓娟.卫星信道的非线性补偿技术研究［D］.秦皇岛：燕山大学，2010.

［4］ Thomas B，Ge′rard F.Nonlinear Channel Modeling and Indentification Using Baseband Volterra-Parafac Models［J］.Signal Processing，2011，92（6）：1492－1498.

［5］ Hyun W K，Yong S C，Dae H Y.An Efficient Adaptive Predistorter for Nonlinear High Power Amplifier in Satellite Communication［J］.IEEE International Symposium on Circuits and Systems，1997，4（9／12）：2288－2291.

［6］ 王晓里，曲强.基于的非线性信道的辨识［J］.计算机仿真，2008，25（5）：129－131，221.

［7］ 张晓娟，吴长奇.使用变步长频域LMS算法的自适应Volterra均衡器［J］.电路与系统学报，2012，17（4）：99－102.

［8］ Saleh A A M.Frequency-Independent and Frequency-Dependent Nonlinear Models of TWT Amplifiers［J］.IEEE Tran on Comm，1981，29（11）：1715－1720.

［9］ 许光飞，张邦宁，郭道省.卫星信道高阶APSK调制的非线性失真补偿算法［J］.电讯技术，2010，50（4）：69－73.

［10］ 张家树，肖先赐.用于混沌时间序列自适应预测的一种少参数二阶Volterrra滤波器［J］.物理学报，2001，50（7）：1248－1254.

［11］ 张艳萍，崔伟轩.引入动态动量因子的共轭梯度多模盲均衡算法［J］.河南科技大学学报：自然科学版，2013，30（3）：40－44.

［12］ 郭业才，袁涛，章涛.气象卫星信道模拟器的设计及其仿真［J］.计算机应用，2013，33（9）：2650－2652.