再入飞行器压心测量方法研究
秦永明,魏忠武,董金刚,陈 强,张 江
(中国航天空气动力技术研究院,北京 100074)
0 引 言
对于载人飞船返回舱等再入飞行器来说,其长细比和升阻比都比较小,如“联盟”、“双子星座”、“阿波罗”等,其升阻比为0.1~0.5,长细比为0.88~1.53[1]。而对于小升阻比载人返回飞行器的再入流谱比较复杂,在配平攻角下,迎风区一般为附着流,背风区和底部一般为分离流区,绕流流场内存在驻点区、亚声速流区、超声速流区、无粘激波层、粘性混合区、尾涡区、头激波、尾激波和压缩波、边界层等[2-3]。这些流谱对载人返回飞行器表面的压力分布有直接影响,而压力中心的位置会影响飞行器的配平攻角及稳定性[4]。
对于小升阻比飞行器,压心的位置对飞行器性能影响较大,如减小压心位置调整系数对末制导炮弹的捕获区域的增大有利;准确地确定弹体压心位置是编制高精度射表的前提条件之一[5-6];质量矩控制对飞行器对压心最大容许偏差范围也提出了更高的要求[7-13],等等。而对于某些飞行器,风洞实验的常规处理方法中不能给出的飞行器真实的压心,如:对于头部具有很高肩部的前伸杆形超声速尾翼式破甲弹,在攻角不等于0时,尾翼的法向力和肩部偏心的压差轴向力对全弹的稳定性都有贡献;对于头部带阻力环的超声速火箭弹,在有攻角时阻力环偏心的压差轴向力对全弹的稳定性也有影响;对于带柔性飘带子弹,弹体为平头短圆柱外形,有攻角时弹体迎风面上作用着偏心的轴向力,弹体和飘带的轴向力对稳定性都有贡献等。以上情形由于轴向力对俯仰力矩均有贡献,如果按风洞试验的常规处理方法给出的压心系数是不准确的。
要准确测量飞行器的实际压心位置,需要从天平设计、测量技术、数据处理方法等各方面共同努力提高才能解决。本文主要从数据处理方法方面对小升阻比再入飞行器压心测量方法进行了探究,得到了压心的准确位置,进一步分析了法向力和轴向力对俯仰力矩的影响。
1 常规风洞试验中飞行器压心的测量
1.1 常规飞行器压心的测量计算方法
若CN≠0,则cp按下式计算:

若α→α*时,CN→0,Cm→0,且CNα≠0,则α=α*时的¯xcp按下式计算:

其中,CN是飞行器的法向力系数,Cm是对飞行器质心的俯仰力矩系数,是飞行器头部顶点到质心的距离,lxcp为¯xcp的参考长度,l3为俯仰力矩系数参考长度。
从压力中心计算公式中可以看出,压力中心的大小取决于俯仰力矩系数Cm和法向力系数CN,而俯仰力矩是由法向力和轴向力共同产生的,所以在常规风洞测力试验中压力中心的计算是将轴向力产生的俯仰力矩等价为法向力额外产生的俯仰力矩,而且求得的压力中心是飞行器受到空气动力合力R与飞行器纵轴的交点。
飞行器在飞行中受到气动力的作用,其中法向力和轴向力均会引起对飞行器质心的俯仰力矩[15]。对于常规外形飞行器,轴向力一般较法向力小一个量级或者更多,而且轴向力对质心的力臂要比法向力对质心的力臂小得多,从而轴向力对俯仰力矩的贡献是次要的,所以对于常规布局飞行器,利用常规计算公式可以近似得到飞行器压力中心的位置。并且在攻角不大的情况下,常近似地把总升力在纵轴上的作用点作为飞行器的压力中心[16]。
1.2 再入飞行器压心测量的困难
对于小长细比再入飞行器,其升阻比比较小,小攻角时轴向力大于法向力,而且轴向力对质心的俯仰力矩和法向力对质心的俯仰力矩的量值相当,而且随着攻角的增加,轴向力对俯仰力矩的贡献逐渐增加,并逐渐大于法向力对俯仰力矩的贡献,这时对质心的俯仰力矩主要是由轴向力提供的,这时如果依然使用式(1)和式(2)的方法来计算压力中心,则误差较大,而且无法真实反映出飞行器的真实压心位置。
如图1所示,在常规测力风洞试验中,测量天平可以测量出飞行器的气动力和对天平参心的气动力矩,如此只能得到气动力R(即轴向力与法向力的合力)的大小、方向及气动力对天平参心力臂d的大小,如果利用常规的压力中心计算方法,则求得的压力中心位置为气动力与飞行器纵轴的交点CP′,而不是飞行器压力中心的准确位置CP。
2 再入飞行器压心准确测量解决方案
风洞试验中,从静态的测量方式,天平测量飞行器的气动力和力矩,只能得到轴向力与法向力合力的大小、方向及该合力力臂的大小,无法得到合力的作用点即压心的位置。而从动态的观点来看,飞行器在攻角连续变化时,其所受到的气动力和力矩是连续变化的,则其压力中心也是连续变化的。飞行器在攻角变化时,其所受到的气动力合力在体轴系中的方向也会发生变化,即气动力合力在体轴坐标系中是随攻角变化旋转的,压力中心即为是合力作用线的旋转中心,但该旋转中心的位置随攻角应是变化的。
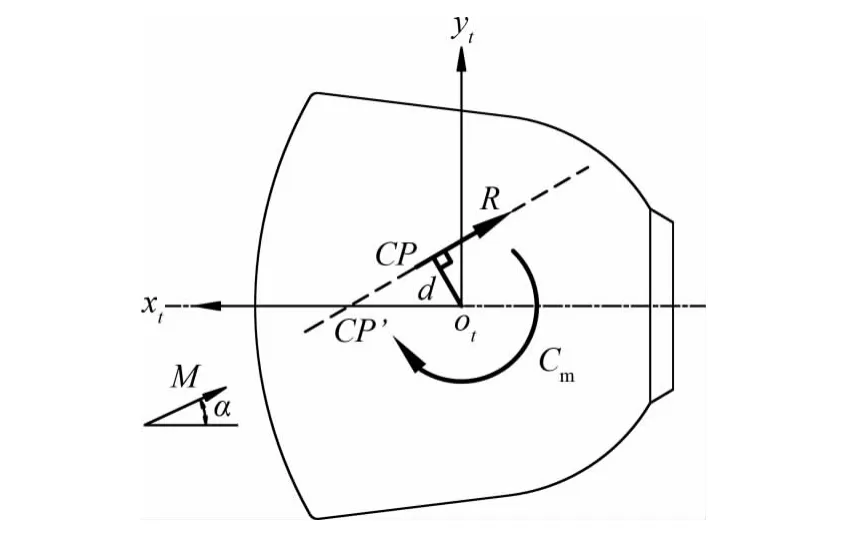
图1 飞行器受力示意图Fig.1 The schematic of force on re-entry aerocraft
假设再入飞行器攻角为α时,参见飞行器坐标系示意图2,压力中心在弹体坐标系(xtotyt)下坐标为(xP,yP),则下式成立:


图2 飞行器坐标系示意图Fig.2 The coordinate system schematic of re-entry aerocraft
当返回器攻角变化很小且为(α+△α)时,压力中心坐标满足等式:
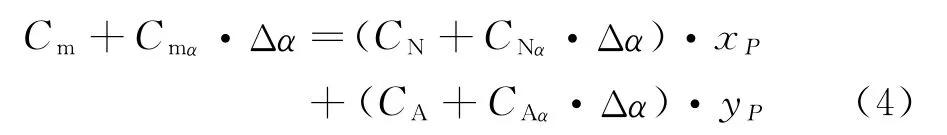
其中Cmα、CNα和CAα分别是Cm、CN和CA对攻角的导数。

综合式(3)、式(4)可求得:故在返回器本体坐标系(xoy)下,压力中心的坐标为
3 准确测量试验方法与结果
对于上述压力中心测量和计算方法,除了测量飞行器在每个姿态下的气动力之外,还需要得到飞行器在每个状态下气动力随攻角变化的导数。在常规试验中,攻角机构采用阶梯站位变化形式,测量的攻角个数较少,以此求得气动力随攻角变化导数的误差较大,从而得到压力中心的误差也比较大。随着风洞试验测试技术的发展,近年已有风洞在进行定常测力试验时采用攻角连续变化和数据实时采集的试验技术,这些技术不仅可以明显减少试验吹风时间,降低试验成本,更能够大幅度增加试验数据的数量,精确反映被研究对象气动特性随攻角变化的规律。
3.1 攻角连续变化和数据实时采集试验技术
攻角连续变化和数据实时采集试验技术主要包括风洞流场控制、攻角连续变化控制及数据实时采集与处理等三个方面。试验时,系统控制风洞启动,当流场建立并稳定后,攻角控制系统开始控制攻角机构偏转,当机构到达给定攻角起点并开始匀速变化时,数据采集系统开始对气流参数、攻角和天平输出按对应时序实时同步采集,直到攻角机构到达攻角范围终点,机构快速回零,风洞关车,数据采集系统采集末零,试验结束。对于超声速风洞试验来说,当风洞阻塞比满足要求,只要攻角变化速度适合,就能获得稳定的流场。
经过标模试验以及大量型号试验的对比与分析,连续攻角试验结果与阶梯攻角试验结果一致性很好,满足试验精准度要求,表明连续攻角变化采集的试验数据结果可靠。图3为M=2.01时AGARD-B标模测力试验中连续攻角与阶梯攻角的部分气动特性曲线对比。其中连续攻角试验中,攻角的运行速度为3°/s,采集频率为100Hz。
3.2 试验结果与分析
攻角连续变化运行方式可以得到模型随攻角变化的非常密集的试验数据,对这些数据点进行曲线拟合,得到再入飞行器气动力和力矩随攻角变化的函数关系。使用本文的方法,可以得到压力中心随攻角的变化规律以及不同攻角处CN和CA分别对Cm的贡献量。图4为某再入飞行器压力中心随攻角变化示意图(M=4.0),从图4可以看出,随着攻角的负向增大,压力中心的位置沿着轴向前移,并逐渐远离模型的对称轴。

图3 连续攻角与阶梯攻角下标模气动特性曲线(M=2.01)Fig.3 The comparison of standard model experiment with attack angle continuous change and discontinuous change
图5为压心位置坐标随攻角变化曲线,图6为CN、CA对Cm的贡献情况。图中数据点为计算结果的部分样点数据。
定义CN对Cm的贡献为:

定义CA对Cm的贡献为:

从图5、图6中可以看到,在攻角较小时压力中心常规计算值较压力中心轴向位置靠前,此时CA对产生的Cm为负值;在α=-10°附近,压力中心常规计算值和压力中心轴向位置相同,此时CA作用点在飞行器的对称轴上,其对Cm的贡献为0,Cm完全由CN提供;随着攻角的负向增加,CA对Cm的贡献逐渐增加,CN对Cm的贡献逐渐减小并成负值,压力中心轴向位置坐标值xP和常规计算值中压力中心和纵轴交点坐标值xcp的差量逐渐增大。而CN和CA在飞行器上合力的作用点偏离对称轴并不是很大,所以压力中心法向位置坐标值yP比较小。

图5 压力中心位置对比图(M=4.0)Fig.5 The comparison chart of pressure center
4 结 论
(1)对于再入飞行器,本文计算方法可以得到飞行器压力中心的准确位置。研究发现,在飞行器攻角较大时,飞行器压力中心坐标值与常规计算值差异较大,主要原因是:常规计算中近似认为Cm完全是由CN产生的,常规计算值为飞行器受到的气动力与飞行器纵轴的交点坐标值;对于再入飞行器,一定攻角范围内,CA大于CN,且Cm主要是由CA产生的,CN对Cm的贡献量很小甚至为负值,此时需要仔细分析CA和CN对Cm的影响量。
(2)本文计算方法需要测量飞行器气动力和力矩对攻角的导数,而采用攻角连续变化运行方式进行数据的实时采集,可以得到飞行器固定状态附近比较密集的试验数据,为计算的准确性提供保障。
(3)通过本方法可以解决再入飞行器压力中心的准确测量与预测的问题,获取压力中心准确位置及其随攻角变化规律,对于再入飞行器质心位置设计和姿控系统设计具有很好的参考意义。
[1]赵梦熊.载人飞船空气动力学[M].北京:国防工业出版社,2000.
[2]MOSELEY W C,WELLS B J.Wind tunnel investigation of the aerodynamic pressures on the apollo command module[R].NASA TN D-5514,1969.
[3]LEE D B.The aerothermo dynamic environment of the apollo command module during super orbital entry[R].NASA TN D-6792,1972.
[4]任玉荷.关于非对称外形再入飞行器的压力中心系数的新定义[J].空气动力学学报,1987,5(1):93-96.
[5]张进忠,宋卫东,成政.弹体压心位置变化对末制导炮弹弹道的影响[J].军械工程学院学报,2009,21(2):32-35.
[6]宋卫东,张进忠.末制导炮弹弹道模型研究综述[R].弹道学术交流会论文集[C].南京:南京理工大学,2007:1552160.
[7]魏鹏鑫,高长生,荆武兴.质量矩控制飞行器的压心不确定性问题研究[J].航天控制,2012,30(2):39-45.
[8]YU Y F,YANG J,YANG C,et al.On proper consideration of center of gravity and pressure center in design of air-to-air missile[J].Journal of Northwestern Polytechnical University,1998,16(1):42-46.
[9]SUN W H,LI G F.Attitude control of moving mass reentry vehicle using passivity-base techniques[J].Journal of Astronautics,2008,29(4):1314-1319.
[10]LI R K,GAO C S,JING W X,et al.Moving mass control and performance analysis for aerospace vehicl[J].Journal of Astronautics,2010,31(9):2165-2171.
[11]ZHOU F Q,CUI L M,ZHOU J.The control of ballistic warhead with variable centroid[J].Journal of Astronautics,2000,21(s):107-110.
[12]叶尧卿.便携式红外寻的防空导弹设计[M].北京:中国宇航出版社,2006:441-448.
[13]王春梅.气动载荷压心变化对机翼结构重量的影响[J].应用力学学报,2012,29(2):197-200.
[14]范洁川.风洞试验手册[M].北京:航空工业出版社,2002.
[15]吴子牛.空气动力学[M].北京:清华大学出版社,2007.
[16]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2008:171-174.

