低雷诺数翼型的气动外形优化设计

陈学孔，郭 正，易 凡，王瑞波，刘光远，李泓兴

（1.中国空气动力研究与发展中心 高速空气动力研究所，绵阳 621000；2.国防科学技术大学 航天与材料工程学院，长沙 410073）

0 引 言

翼型的选型和设计是飞行器气动设计中的一项基础性工作，翼型对飞行器的气动性能具有根本性的影响。现在的高性能飞行器已不再从翼型库中选择适用翼型后直接使用，而是以该翼型作为基准翼型进行气动优化，获得能满足飞行器性能要求的专用翼型［1－2］。基于数值计算的气动正优化是当前气动外形优化设计领域的主要方法。

传统的翼型气动外形优化研究主要针对雷诺数为107量级的大型亚跨声速飞行器翼型，对此有着较为深厚的技术积累。然而，近十年来，雷诺数在104～105量级之间的低雷诺数翼型随着微小型无人机的快速发展和高空低速太阳能飞行器的研制而产生了广泛的应用需求，有必要对低雷诺数翼型进行专门研究。低雷诺数翼型与传统的高雷诺数翼型存在差异。低雷诺数翼型厚度小且变化缓慢，Goe系列、Sd和Eppler系列翼型多可作为低雷诺数翼型使用。低雷诺数条件下绕翼型的流动一般为层流，边界层内流动动量难以克服逆压梯度的影响，流动容易过早分离，对气动性能产生影响，且气动性能对雷诺数变化敏感，对气动外形的依赖性也较强［3－4］。普通的翼型气动优化目的一般是为了提高飞行器的气动效率，高雷诺数翼型的优化目的在于获取升阻比最优翼型，而低雷诺数翼型以提升功率因子为优化目的更具实际意义。

目前，针对低雷诺数翼型的气动外形优化设计研究相比传统翼型还不是很丰富。国外［5－6］和国内［3，7－8］均对低雷诺数翼型进行了气动外形优化研究。左林玄［3］等对低雷诺数翼型进行了功率因子和力矩系数的加权单目标单点优化，李军鹏［7］等进行了降低不确定性的稳健优化，张亚锋［8］等进行了以升阻比为目标的单点优化。翼型气动外形优化方法的环节较多，作为优化前提的翼型参数化方法就有Parsec Method、Hicks－Henne型函数、B－spline Curves、Mesh points、CST等方法，其中Hicks－Henne型函数和Parsec（Parametric Section）方法是国内外常用的参数化方法，前者是通用方法，后者多见于超临界翼型Rae2822的气动优化研究［1，9－10］。在低雷诺数翼型参数化研究中，张亚锋［8］使用 Hicks－Henne型函数，左林玄［3］、王建军［11］对 Hicks－Henne型函数进行了改进，李军鹏［7］使用Parsec方法对E186翼型进行了优化。此外，当前的低雷诺数翼型气动优化多是单点优化和稳健优化，多点优化研究则极为少见。

基于数值计算的气动正优化问题中，一套成熟高效的方法是首先对翼型进行参数化，然后进行试验设计取样，再应用数值计算技术获取样本翼型的气动特性，最后通过代理模型和优化算法的结合搜索获得气动性能最优的翼型。本文亦采用此类方法进行研究工作，论述了功率因子对低雷诺数翼型的重要性；研究了低雷诺数翼型参数化方法，特别对常见的Parsec方法应用于低雷诺数翼型参数化描述的质量进行了研究；最后把常用于高雷诺数翼型的多点优化技术应用于低雷诺数翼型研究中，进行速度域跨度10m／s和15m／s的两组、每组两种不同加权系数的多点优化，同时也进行了单点优化，并分析比较了单点和多点优化结果。

1 优化目标分析

气动外形优化设计的目的在于实现翼型良好的气动效率，满足飞行器的性能需求。航时和航程是飞行器设计中考虑的重要问题，也成为翼型气动优化的重要目的。从航时角度考虑，亚跨声速内飞行的飞机，在最佳续航和升阻比最大状态下的航时最长［12］。因此传统高雷诺数翼型气动优化的目标是获取升阻比最大的翼型。而对于低雷诺数条件内的飞行器，翼型气动外形优化目标从功率因子方面考虑有利于实现航时延长的目的。升阻比K＝CL／CD与功率因子PI＝／CD从公式形式接近，实际中，翼型升阻比最大时的功率因子不一定最大，反之也成立。图1显示的是Sd7032翼型在雷诺数3.85×105条件下，升阻比和功率因子随迎角变化的情况。

图1 Sd7032翼型气动性能随迎角变化示意图Fig.1 Aerodynamic characteristics changed with angle of attack of Sd7032

低雷诺数范围内带动力的低速小型飞行器，平飞状态下的功耗可以简化表示为［13］：

式中，W 是飞机飞行总质量，ρ为来流密度，S为机翼面积，并定义功率因子。式中翼载荷W／S固定时，PI越大，飞行器功耗越小，飞行时间越长，这对希望延长航时的现代小型长航时无人机具有积极作用。因此，低雷诺数翼型的气动优化从功率因子角度考虑能获得满足低速小型飞行器航时性能要求的优化翼型。

2 数值计算方法

低雷诺数条件下，绕翼型的流动常在逆压梯度的影响下出现分离，并伴随层流或湍流分离泡的产生和附着，分离泡区域的大小比例在不同的雷诺数下不尽相同［3－4，14］，使得翼型的流场变得极为复杂。通过数值计算的方法模拟求解低雷诺数翼型的气动特性，需要准确捕捉以上现象并进行细致的分析，XFOIL程序恰好满足了要求，计算数据有效，并有广泛使用。

XFOIL由美国MIT的Mark Drela博士编写［15］，针对低雷诺数条件下翼型的数值模拟而专门开发的流场求解的开源程序，是国外进行低雷诺数翼型计算的主要工具，其准确性和可靠性在多篇文献中都得到验证应用，多年来该程序得到不断改进并完善。国外文献［6，16］、国内文献［3－4］使用的数值模拟求解器是XFOIL，文献［4］对其计算的准确性进行了专门验证。作者使用XFOIL前也对其进行了验证，计算了文献［4］的算例并进行对比，还通过文献［17］计算了其中的Eppler387翼型的气动性能并与风洞试验结果进行对比，结果表明，XFOIL数值计算的数据比较准确地反映了真实流场中翼型的气动特性。

3 翼型参数化方法研究

翼型的参数化描述方法包含多项式拟合法和解析函数线性叠加法等多种方法，如引言中提及的方法。本文选取国内外广泛使用的Hicks－Henne型函数和Parsec方法对低雷诺数翼型进行参数化研究。

3.1 Hicks－Henne型函数参数化研究

Hicks－Henne型函数［18］适合对任何翼型进行参数化描述，直观并易于控制。然而原始的Hicks－Henne型函数的函数项中没有对翼型尾缘点的控制函数，使翼型尾缘部分参数化空间得不到拓展，影响优化翼型质量［11］。要解决此问题，理论上使用无限多的型函数对翼型进行控制即可，但产生的计算量非常大，且效果并不突出。文献［3］和文献［11］对Hicks－Henne型函数进行了改进，文献［3］添加翼型前缘和尾缘的控制函数，文献［11］通过另一种形式的函数对翼型尾缘进行控制，两种改进方法产生的效果差别不大。本文以文献［11］中改进的Hicks－Henne型函数作为低雷诺数翼型参数化方法，即在原Hicks－Henne型函数中设计fn（x）＝αx（1－x）e－β（1－x）函数项，该函该在x＝1处一阶导数值不为0，可以改变参数化翼型的尾缘夹角，使参数化空间得到拓展。公式为：

以上式子中，yup、ylow表示翼型的上、下表面函数；y0up、y0low表示基准翼型的上、下表面函数；n为型函数数目；fk（x）为型函数；ck为设计变量，对翼型的外形进行约束，取值范围根据经验而定，无取值公式参考。

图2显示了使用Hicks－Henne型函数和改进Hicks－Henne型函数参数化描述的低雷诺数翼型尾部效果图，图2（a）图形使用改进的 Hicks－Henne型函数描述，图2（b）使用原始Hicks－Henne型函数描述。由图2可见，改进Hicks－Henne型函数有效实现了参数化翼型尾缘夹角的改变。

图2 改进的Hicks－Henne型函数和原始Hicks－Henne型函数参数化翼型图Fig.2 Images of Sd7032parameterized by improved and initial Hicks－Henne shape functions

3.2 Parsec方法参数化研究

Parsec方法［19］是国内外使用非常广泛的另一种翼型参数化方法，把翼型分为上下两个型面，通过以下公式进行描述：

式中各参数的求解可参考文献［20］。Parsec方法使用12个参数对翼型控制，示意图如图3所示。

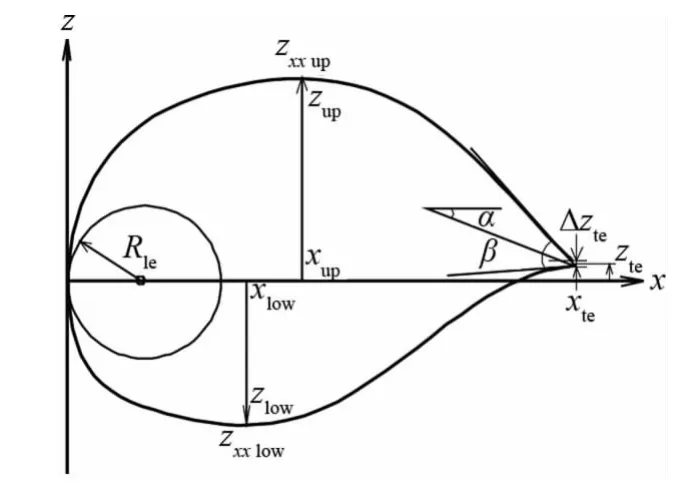
图3 Parsec方法示意图Fig.3 Schematic of parsec method

目前，Parsec参数化方法在超临界翼型Rae2822的研究案例中较为常见［1，9－10］，能否应用到低雷诺数翼型中还尚未形成结论。文献［7］使用Parsec方法对Eppler186翼型进行参数化描述，本文以Sd7032翼型为例，使用该方法对其进行多次描述，效果最好的一次参数取值范围列于表1中，参数化描述结果如图4所示。

图4 Parsec方法描述的参数化翼型Fig.4 Airfoil shapes parameterized by Parsec method

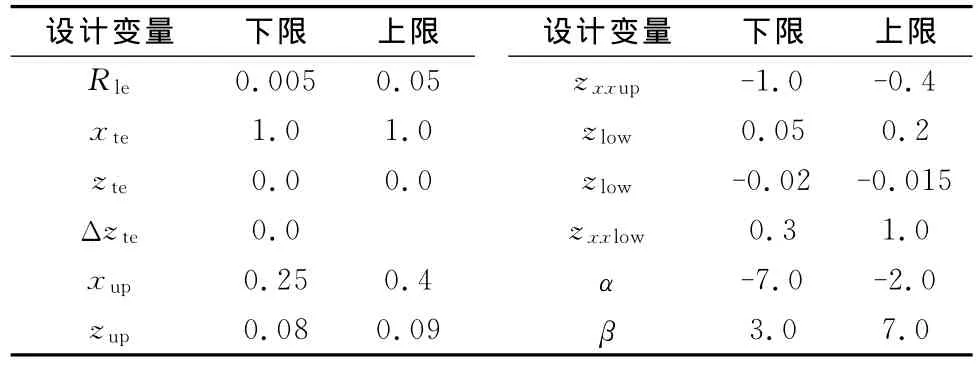
表1 Parsec设计变量取值范围Table 1 Ranges for design parameters of parsec method

图4显示的12个参数化翼型，畸变严重，不符合基本的翼型规范。鉴于Parsec方法对Rae2822和Eppler186翼型有过参数化案例，把Rae2822、Sd7032和Eppler186翼型显示于图5进行分析，由图5可见Rae2822与Eppler186翼型曲线相对弦线的变化空间比较大，而Sd7032翼型下翼面曲线相对弦线变化空间较为有限，并且存在明显的极小值和极大值两个点。作者分析认为，Parsec方法使用12个参数（最少9个）拟合翼型曲线，以较少的设计变量减小了描述翼型的工作量，实际中却使得设计变量的取值范围变得更为模糊，人工给定的参数范围往往脱离“真实”范围，致使参数化的翼型不合格数量增多，质量变差。Parsec方法描述相对弦线两侧曲线开度较大的翼型时能取得一定效果，但是对曲线开度很小的翼型，需要慎重使用。Parsec方法描述构型曲线的二阶导数明显为0的翼型时，还应该增加约束条件。

图5 Rae2822、Sd7032和Eppler186的外形图Fig.5 Shapes of Rae2822，Sd7032and Eppler186

4 单点优化与多点优化

单点优化和多点优化是气动外形优化中的两种优化方式。单点优化是对翼型在一个“点”处进行气动外形优化，如马赫数设计点或速度设计点等。多点优化是在连续的设计区域内取多个“点”，通过权函数综合翼型在各“点”处的气动性能进行的优化，实现优化翼型在该设计区域内的气动性能整体最优，避免飞行过程中不确定因素（如突风、气流密度变化等）的影响，改善飞机偏离单点工况后翼型气动性能恶化的状态，使飞行器在设计区域内实现平稳飞行［21－24］。

基于数值计算的气动正优化方法在单点优化和多点优化两种方式上都能实现良好的运用，是气动优化设计领域的重要研究手段。本文翼型参数化方法使用改进的 Hicks－Henne型函数［11］，采用均匀试验设计方法［25］取样，运用XFOIL程序对样本翼型进行数值计算，通过Kriging代理模型和遗传算法的结合，搜索获得满足约束条件的全局最优解。进行单点和多点优化时，根据低雷诺数翼型的特点，从基于功率因子最大的角度进行优化，优化目标没有直接设为功率因子，而是设成阻力系数最小，约束条件中对升力系数的1.5次幂和力矩系数施加约束，从间接层面实现了功率因子的最大，并兼顾了翼型良好的气动效率。单点和多点优化思想可以用数学式子表述为：

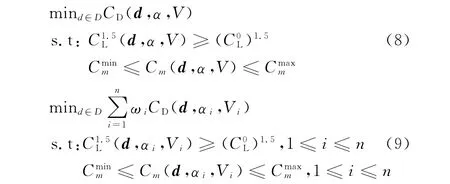
式（8）为单点优化公式，式（9）为多点优化公式。式（8）中的D代表设计空间，d为设计变量向量，α为迎角，V 为来流速度为升力系数的约束下限，和分别表示力矩系数的约束上下限；式（9）中的n代表设计点数目，ωi、αi和Vi分别代表第i个设计点的权重系数、迎角和来流速度，其它符号的含义与式（8）相同。

5 优化案例及分析

选择Sd7032翼型进行单点和多点优化，多点优化翼型的性能和权重系数与连续设计区域范围有关联，本文的多点优化是取两组不同设计域、每组两种不同权重系数的优化，最后分析比较了单点优化和多点优化结果。

5.1 单点优化

Sd7032翼型在迎角4°，速度17m／s，雷诺数3.5×105下优化。参数化方法使用文献［11］中改进的Hicks－Henne型函数，取6个型函数，对应节点0、0.2、0.4、0.6、0.8、1.0。约束条件为表2中12个设计变量的几何约束和性能约束：≥0.95，－0.12≤Cm≤－0.09。

表2 改进的Hicks－Henne型函数设计变量取值范围Table 2 Ranges for design parameters of improved Hicks－Henne shape functions

5.2 多点优化

对Sd7032翼型进行2组4次气动优化，分别记为Multi11、Multi12、Multi21和 Multi22。四个优化案例均在迎角4°下进行，参数化方法选择和设置与5.1节单点优化案例相同，其它条件具体为：

Multi11：设计速度域［12m／s，22m／s］，跨度10m／s，设计点12m／s、15.33m／s、18.67m／s、22m／s共四个，对应权重系数为0.25、0.25、0.25、0.25；优化约束条件为12个设计变量的几何约束和性能约束－0.09（i＝1，2，3，4）；直接目标为权阻力系数最小。

Multi12：设计速度域、设计点、约束条件与Multi11相同，权重系数为0.15、0.35、0.35、0.15。

Multi21：设计速度域［7m／s，22m／s］，跨度15m／s，设计点7m／s、12m／s、17m／s、22m／s共四个，权重系数和Multi11相同，约束条件为12个设计变量的几何约束和性能约束4）以及力矩系数约束条件＝1，2，3，4）；直接目标为权阻力系数最小。

Multi22：设计速度域、速度点、约束条件与Multi21相同，权重系数与Multi12相同。

多点优化得到的四个优化翼型在4°迎角下各自速度域内的气动性能，与Sd7032翼型的对比情况展示于图6和图7中，单点优化翼型的性能也一并列于图中。

5.3 分析比较

图6和图7显示了Sd7032翼型的单点和多点优化性能变化。表3和表4列出了对基准翼型、单点优化翼型和多点优化翼型在对应设计速度域内性能均值和方差的分析结果，表3对应的速度域为［12m／s，22m／s］，表4对应的速度域为［7m／s，22m／s］，各速度域取7个均分点研究。

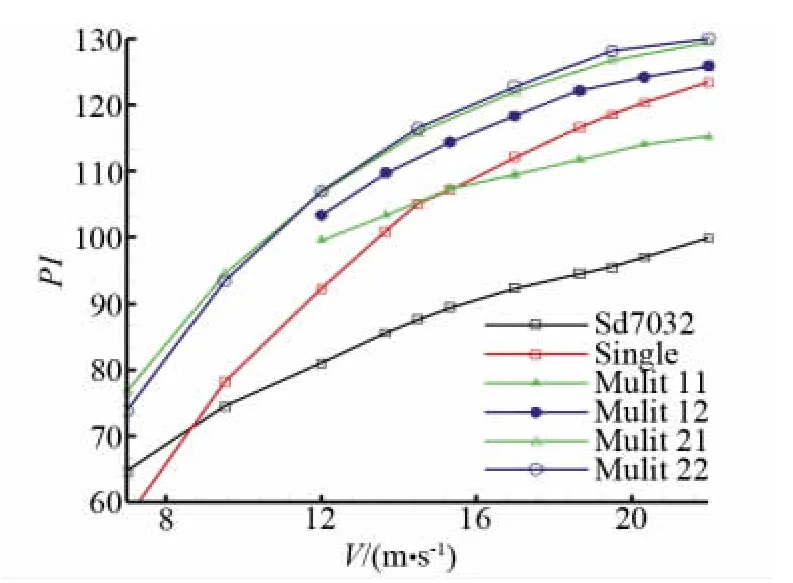
图6 翼型的功率因子变化对比图Fig.6 Curves of power index change with speed

图7 翼型的力矩系数变化对比图Fig.7 Curves of moment coefficient change with speed

表3 速度域［12m／s，22m／s］内各翼型性能变化Table 3 Aerodynamic performances change in speed range［12m／s，22m／s］for each foil

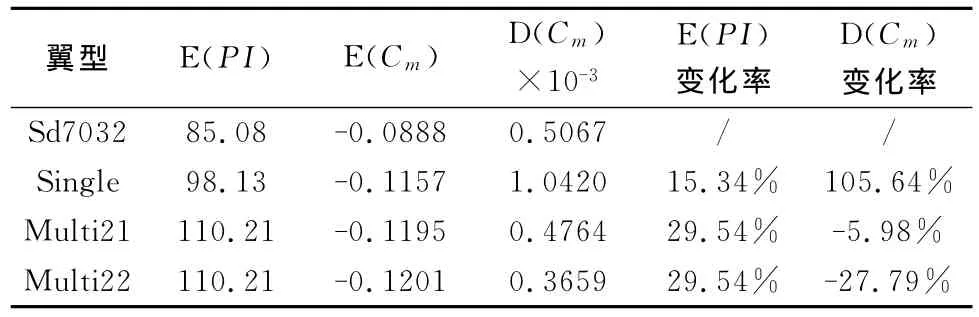
表4 速度域［7m／s，22m／s］内各翼型性能变化Table 4 Aerodynamic performances change in speed range［7m／s，22m／s］for each foil

分析可知，单点和多点优化均实现了翼型功率因子性能的提高，多点优化提高幅度较大，最高达到29.54%；单点优化在设计点17m／s处使功率因子提高21.37%，但图6显示其在速度约9m／s以前，功率因子小于基准翼型。说明在低雷诺数范围内，多点优化可以实现连续设计域内翼型性能的提高，而单点优化则不能保证在非设计点处始终处于优化状态。图7显示了力矩系数的变化，整体上看优化后的翼型力矩系数发生较大变化；个体上看，基准翼型力矩系数的绝对值｜Cm｜随速度的增大而增大，而多点优化翼型｜Cm｜则出现缓慢减小趋势，变化紧凑，单点优化翼型｜Cm｜的变化幅度较大，该情况在表3和表4中有精确体现，多点优化翼型力矩系数方差优于基准翼型，而单点优化翼型力矩系数方差高于基准翼型，增大一倍以上。说明低雷诺数范围内，多点优化可以控制翼型在设计区域内的力矩系数变化，实现平稳飞行，而单点优化不能保证此效果的完全实现。图7中，相对基准翼型，优化翼型力矩系数变化较大是优化过程中损失力矩性能换取功率因子最大化的结果，气动优化中可以对｜Cm｜施加更小的约束保证力矩性能与基准翼型相当，但会对间接的优化目标产生较大影响，限制翼型功率因子的优化幅度。此外，｜Cm｜的约束值需要根据翼型参数化过程中设计变量的取值范围而合理设置，也要考虑工程中对翼型力矩系数的控制能力。在本文的多点优化案例中，进行了两种不同权系数的优化，权系数的功能是通过权值大小控制翼型优化性能在设计点处的表现，权值越大，翼型性能在该点的表现越突出。从图6的曲线分析，权系数对本文优化效果的改变表现微弱，在权系数值不均等的Multi12和Multi22曲线上，权系数值为0.35的设计点处的功率因子点有较小突起。

本文以Sd7032翼型为基准翼型，实现了单点和多点优化翼型性能的提高，其中Multi22多点优化翼型功率因子均值提高29.54%，力矩系数方差降幅27.79%，力矩系数变化更稳定，可以用于低雷诺数飞行器，实现降低功耗而延长航时的目的，并具备提高平稳飞行的能力。图8显示了多点优化Multi22翼型和基准翼型Sd7032在速度17m／s、迎角4°时的压力系数分布图，以及两个翼型的外形对比图，图9显示的是可以在工程中应用Multi22翼型的某大展弦比长航时低速太阳能无人机的气动布局图。

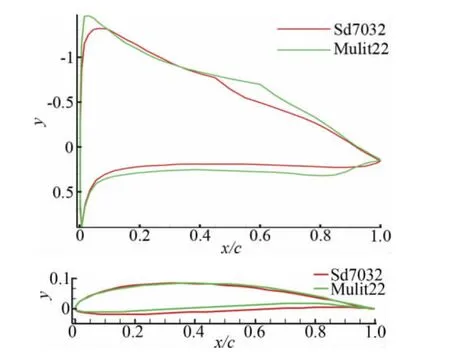
图8 优化翼型和初始翼型压力分布及外形对比图Fig.8 Pressure distribution and shape comparation of initial and optimized airfoils

图9 太阳能无人机气动布局图Fig.9 Aerodynamic layout of a solar UAV

6 结 论

本文通过数值计算的正优化方法对低雷诺数翼型进行了气动外形优化设计研究，对翼型参数化方法进行了比较分析，并进行了单点优化和不同速度域不同加权系数的多点优化研究，获得了低雷诺翼型气动外形优化设计的普遍性参考方法和结论。

（1）参数化方法Parsec不适宜模拟相对弦线开度较小的曲线构型翼型；改进的Hicks－Henne型函数是低雷诺数翼型参数化的可靠办法，能有效提高质量和效率。

（2）传统高雷诺数翼型的单点和多点气动优化结论在低雷诺数翼型优化中有相似结果。本文单点优化翼型在某些非设计点处性能低于基准翼型，且力矩系数随雷诺数变化的不稳定性增加；多点优化翼型在设计范围内性能均处于良好的优化状态，力矩系数方差优于基准翼型，利于提高翼型飞行的稳定性。

（3）增加力矩系数约束的多点优化可以作为设计域跨度较大的低雷诺数翼型的气动优化选择，有较好的工程应用价值。

（4）本文全套优化方法具备良好的全局稳定性，效率较高，可为低雷诺数翼型气动优化提供良好平台。

［1］LIU Z，ZHU Z Q，FU H Y，et al.Design of airfoil with high ratio of lift over drag［J］.ACTA Aerodynamica Sinica，2004，22（4）：410－414.（in Chinese）刘周，朱自强，付鸿雁，等.高升阻比翼型的设计［J］.空气动力学学报，2004，22（4）：410－414.

［2］BAI J Q，WANG B，SUN Z W，et al.The research of robust supercritical airfoil design optimization［J］.ACTA Aerodynamica Sinica，2011，29（4）：460－461（in Chinese）白俊强，王波，孙智伟，等.超临界翼型稳健型优化设计研究［J］.空气动力学学报，2011，29（4）：460－461.

［3］ZUO L X，WANG J J.Airfoil design optimization at low Reynolds number［J］.ACTA Armamentarii，2009，30（8）：1073－1077.（in Chinese）左林玄，王晋军.低雷诺数翼型的优化设计［J］.兵工学报，2009，30（8）：1073－1077.

［4］HE F，SONG W P.Improving the aerodynamic performance of low Reynolds number airfoils in oscillating freestream with forced transition method［J］.ACTA Aerodynamica Sinica，2007，25（4）：495－498.（in Chinese）何飞，宋文萍.固定转捩在改善振荡来流下低雷诺数翼型气动性能中的应用［J］.空气动力学学报，2007，25（4）：495－498.

［5］FOCH R J，AILINGER K G.Low Reynolds number，long endurance aircraft design［R］.AIAA，1992.

［6］LEVIN O，WEI S.Optimization of a flexible low Reynolds number airfoil［R］.AIAA，2001.

［7］LI J P，WANG H P，GE W J.Low speed reflexed airfoil robust optimization design for flying wing configuration［J］.Flight Dynamics，2011，29（1）：17－20.（in Chinese）李军鹏，王和平，葛文杰.飞翼布局低速反弯翼型稳健优化设计［J］.飞行力学，2011，29（1）：17－20.

［8］ZHANG Y F，SONG B F，LI Z K.Aerodynamic optimization design and experiment study for a high lift airfoil［J］.Flight Dynamics，2006，24（4）：70－71.（in Chinese）张亚锋，宋笔锋，李占科.高升力翼型的气动优化设计和实验研究［J］.飞行力学，2006，24（4）：70－71.

［9］LI J Z，GAO Z H.The application of multi－objective evolutionary algorithm and surrogate model to aerodynamic robust optimization design［J］.ACTA Aerodynamica Sinica，2012，30（1）：47－50.（in Chinese）李焦赞，高正红.多目标进化算法和代理模型技术在气动稳健优化设计中的应用［J］.空气动力学学报.2012.30（1）.47－50.

［10］JEONG S，MURAYAMA M，YAMAMOTO K.Efficient optimization design method using kriging model［A］.AIAA Aerospace Sciences Meeting and Exhibit［C］.Reno，Nevada，2004：1－10.

［11］WANG J J，GAO Z H.Analysis and improvement of HicksH－enne airfoil parameterization method［J］.Aeronautical Computing Technique，2010，40（4）：47－49.（in Chinese）王建军，高正红.HicksHenne翼型参数化方法分析及改进［J］.航空计算技术.2010.40（4）：47－49.

［12］FAN L Q.Flight dynamics－computation of aircraft flight performance［M］.Xi′an：Northwestern Polytechnical University Press，2005：49－50.（in Chinese）范立钦.飞行动力学－飞机飞行性能计算［M］.西安：西北工业大学出版社，2005：49－50.

［13］MARTIN S.Model aircraft aerodynamics［M］.London：Special interest model books Ltd.，1999.

［14］SHENG Y H.A study of low Reynolds number performance over a two－dimensional airfoil for micro－air vehilce［D］.Nanjing：Nanjing University of Aeronautics and Astronautics，2003.（in Chinese）盛英华.微型飞行器低雷诺数二元翼型的气动特性研究［D］.南京：南京航空航天大学，2003.

［15］DRELA M.Xfoil：an analysis and design system for low Reynolds number airfoils，low Reynolds number aerodynamics［M］.New York：Springer Verlag，1989.

［16］ALEXANDRE P A，AZEVEDO L F，SILVA R G.A framework for aerodynamic optimization based on genetic algorithms［A］.47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition［C］.Orlando，Florida，2009.

［17］MICHAEL S S，GRANAHAN B D.Wind tunnel testing airfoils at low Reynolds numbers［A］.49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition［C］.Orlando，Florida，2011：986－1000.

［18］HICKS R M，HENNE P A.Wing design by numerical optimization［J］.Journal of Aircraft，1978，15（7）：408－412.

［19］HELMUT S.Parametric airfoils and wings［J］.Notes on Numerical Fluid Mechanics，1998，68：71－88.

［20］SRIPAWADKUL V，PADULO M，GUENOV M.A comparison of airfoil shape parameterization techniques for early design optimization［A］.AIAA／ISSMO Multidisciplinary Analysis Optimization Conference［C］.Fort Worth，Texas，2010：1－8.

［21］HUYSE L，PADULA S L，LEWIS R M，et al.Probabilistic approach to free－form airfoil shape optimization under uncertainty［J］.AIAA Journal，2002，40（9）：1764－1771.

［22］LEE S W，KWON O J.Robust airfoil shape optimization using design for six sigma［J］.Journal of Aircraft，2006，43（3）：843－845.

［23］LIU Y，QIU Z P.Airfoil robust design with uncertainty parameters［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37（1）：41－44.（in Chinese）柳杨，邱志平.翼型气动性能鲁棒性优化设计［J］.北京航空航天大学学报.2011.37（1）.41－44.

［24］PADULA S L，LI W.Options for robust airfoil optimization under uncertainty［A］.9th AIAA／ISSMO Symposium on Multidisciplinary Analysis and Optimization［C］.Atlanta Georgia，2002：1－2.

［25］FANG K T，MA C X.Orthogonal and uniform experimental design［M］.Beijing：Science Press，2001.（in Chinese）方开泰，马长兴.正交与均匀试验设计［M］.北京：科学出版社，2001.