RBF径向基函数与Delaunay图映射技术在飞行器型架外形设计中应用研究
黄江涛,高正红,白俊强,周 铸,赵 轲
(1.西北工业大学 翼型叶栅空气动力学国防科技重点实验室,西安 710072;2.中国空气动力研究与发展中心,绵阳 621000)
0 引 言
飞机气动弹性特性研究传统上划为静气动弹性和颤振特性研究两个独立部分[1-2]。静气动弹性特性计算求解过程往往采用静变形和定常气动力的交替迭代计算,最后得出发散速度或特定飞行条件下的机翼静变形。传统的飞行器设计主要是针对型架外形设计。然而在飞行器经过气动弹性变形之后,巡航状态气动性能与设计性能存在一定的区别。而对于民用客机来讲首先进行巡航外形设计,通过静气动弹性计算、修正得到型架外形,从而保证型架外形在巡航状态飞行时,在气动弹性作用下气动外形与性能能够恢复到巡航设计状态。在型架修正及分析计算方面国内外采用不同的方法进行了不同程度的研究。例如国内杨国伟采用稀疏背景网格进行动网格变形、RBF进行流固耦合,从而实现型架修正以及静气弹分析研究[3],詹浩等采用反设计以及简化结构模型方法进行了机翼型架设计及分析计算[4],国外C B Allen等采用RBF结合TFI技术进行了气动弹性的分析计算[5],取得了合理的计算结果。然而对于气动弹性计算来讲,变形网格的工作效率一定程度上决定了气动弹性分析计算效率,尤其在非定常动气动弹性计算中需要不断的调用变形网格技术,这时网格变形工作效率更为重要。
对于静气动弹性来说,其关键技术为空间网格变形技术以及CFD/CSD数据交换技术。其中变形网格技术效率决定着静气动弹性计算效率、精度,其稳健性决定了能否进行飞行器大运动量下网格变形且能否保持较高网格质量,以及所求气动弹性变形外形的光滑程度;CFD/CSD数据交换技术决定着空气动力学模型与结构模型的数据能否进行高效合理的交换。
本文基于径向基函数与图映射技术建立了高效的网格变形技术,与相关文献不同的是,本文在合理提取飞行器表面稀疏点序列前提下,有效的利用多块网格的块顶点进行Delaunay图映射单元的构建(网格分块尽量均匀),避免了传统Delaunay图单元构建时,相关点输入的复杂操作,并通过RBF技术对网格顶点进行高效操作,实现映射单元变形;通过建立共用的“映射曲面”,实现了CFD/CSD数据高效高精度交换,构建了稳健性强的静气动弹性计算平台;利用该技术对某型支线客机进行了型架外形设计、修正,进一步通过静气动弹性分析计算,验证本文所建立方法的正确性。
1 Delaunay图映射技术
本文建立了基于Delaunay图映射的网格变形技术。Dirichlet图是由一组连接两相邻点直线的垂直平分线组成的连续多边形,而Delaunay三角网是由与相邻Dirichlet多边形共享一条边的相关点连接而成的三角形,换句话说Dirichlet三角网是Delaunay图的偶图。
基于Delaunay图映射的网格变形技术基本依据为:在平面或空间给定包括流场边界点在内的一组点,即可以进行唯一的Delaunay图三角化。在Delaunay图四面体单元构建时,依据球面准则进行交换测试形式的优化,根据插入点坐标定位点所在格网,如果该格网记录有三角形编号,则从该编号开始在相邻三角形中定位插入点所在三角形;由近及远遍历格网的相邻网格,若存在三角编号则遍历结束;在最新生成三角形中定位插入点。从而可以完成计算区域的三角化图覆盖,进一步对空间计算域任意点进行四面体映射单元定位。
计算域网格节点定位完毕后,需建立映射关系[6],对于平面Delaunay三角化背景网格,建立如图1的计算网格与平面Delaunay三角单元关系,对于任意网格节点O处于三角形MNQ中,由O和三角形顶点构造的三角形MON、QOM以及NOQ的面积分别为S1、S2、S3,令:
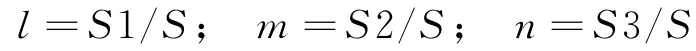
则可以建立Delaunay三角单元节点与计算网格节点如下关系式:
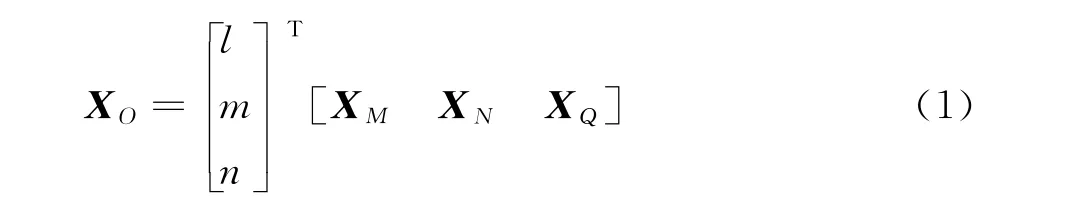
飞行器气动外形变形时,相当于Delaunay图背景网格三角单元变化,即 [XMXNXQ]更新为[X′MX′NX′Q],对于三维网格变形方法与二维原理一致,如图2所示。依据建立的Delaunay图映射关系式,计算网格节点更新为:
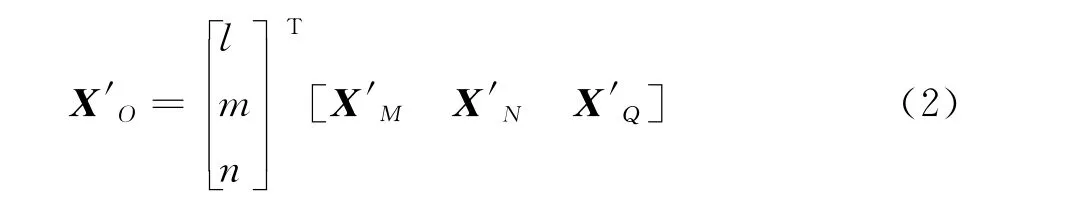
以气动弹性变形后飞行器表面区域顶点位移量为输入量,建立RBF径向基函数插值系统,进行空间区域顶点位移量插值,操作空间网格区域顶点运动,从而进行Delaunay图四面体映射单元的变形,利用式(2)进行计算网格的变形,完成网格更新。而Delaunay映射变换之前首先要完成空间区域顶点的更新,即采用RBF径向基函数技术,其工作示意图见图3。
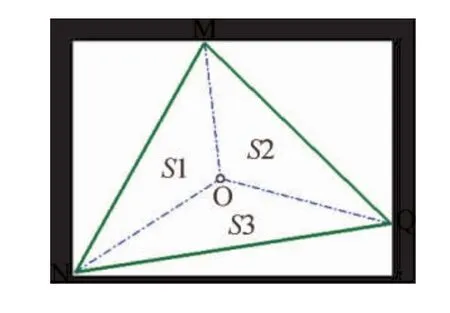
图1 网格节点与Delaunay三角形Fig.1 Grid points and Delaunay triangle
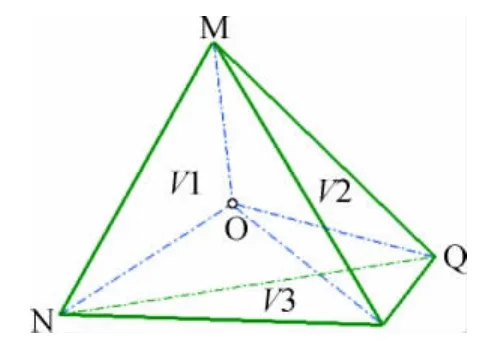
图2 网格节点与Delaunay四面体Fig.2 Grid points and Delaunay tetrahedron
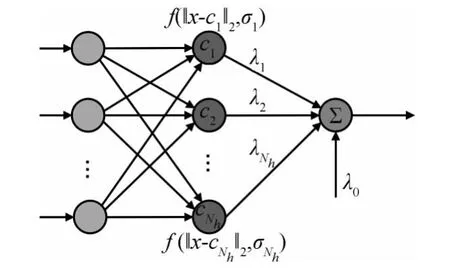
图3 RBF工作示意图Fig.3 RBF work map
2 RBF径向基函数
RBF径向基函数基本概念由Buhmann和Wendland提出[7-8],该技术在精确插值、神经网络构建、数据预测等方面获取了广泛的应用[9-13]。基于RBF方法的插值数学模型可以表示为:
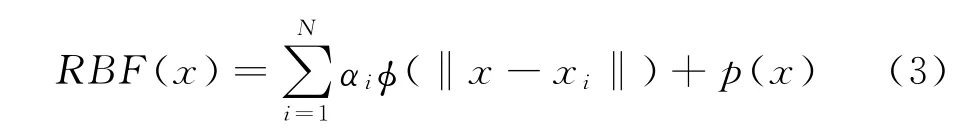
本文对p(x)的选取采用多项式方法:
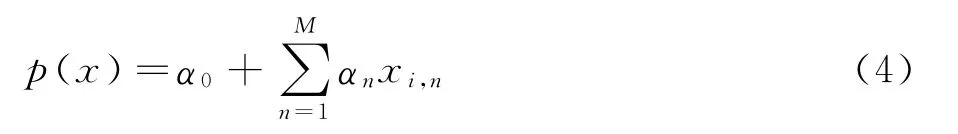
其中M 为径向基中心矢量的维数。p(x)的建立不仅能够精确的描述物体或网格的平移以及旋转运动方式,且进行径向基插值时能够保证输入点系统“力平衡”及“力矩平衡”[14]。其中,xi为径向基中心,相当于图3中ci;αi为插值系数,相当于图3中λi。‖x-xi‖为x到中心xi的径向欧氏距离。且径向基函数φ具有以下性质:
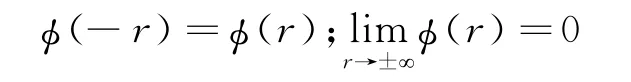
以输入数据为RBF技术构建基础,可以写为如下矩阵形式:
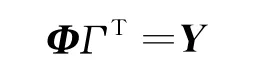
其中:Φ =[φij],φij=φ(‖xi-xj‖),(i,j=1,2,…,N );Φ 为插值矩阵,ΓT=Φ-1Y,Γ = [λ1,λ2,…,λN]。从而实现RBF径向基函数框架构建,RBF(x)则为通过所有输入点的连续可微函数。
3 CFD/CSD数据耦合技术与静力学方程求解
在CFD/CSD数据交换时,本文采用构建空气动力模型与结构模型的共用“映射曲面”[15],根据机翼形状建立一曲面,该曲面由两个方向逻辑参数进行描述,网格中第i行,第j列处的节点坐标为(x,y),且该点处的参数化坐标定义为(u ,v),u =i,v =j。将映射网格控制点参数化后得到参数空间。
对于CFD/CSD网格交界面上节点的参数化就是要计算该点在参数空间中的坐标,首先利用面积坐标方法[15]定位源/目标学科节点所处映射曲面单元(i,j),进一步通过双线性曲面插值计算该点在其所在的结构化映射网格单元内的位置(i0,j0),则该节点在参数空间的位置为(i+i0,j+j0)。
本文采用双三次Bezier曲面[15-16]进行源学科节点与目标学科节点变量插值:
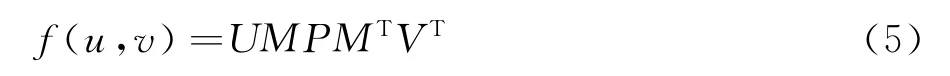
其中,U、V为目标学科参数空间逻辑坐标,P为源学科节点矩阵,M 为Bezier基函数系数矩阵。
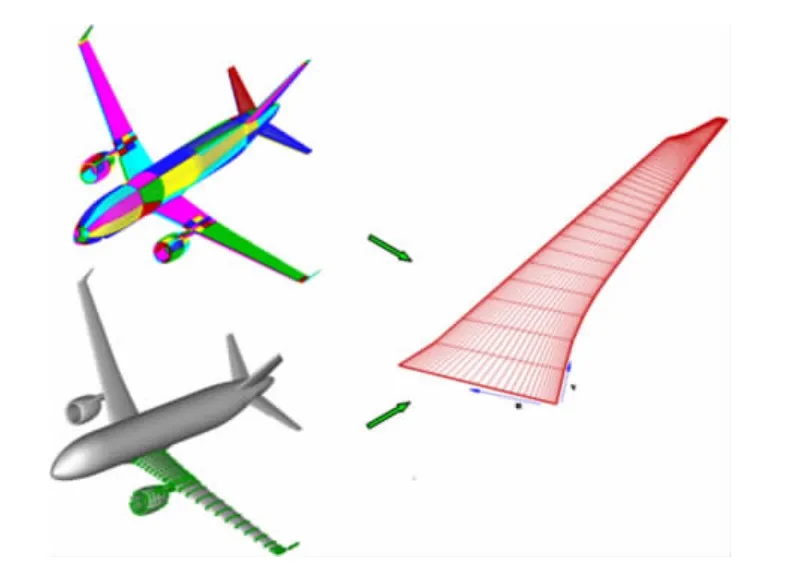
图4 “映射曲面”工作示意图Fig.4 Mapping surface work map
采用柔度系数矩阵方法[17-18]求解结构静力学方程时,仅考虑飞机机翼的弹性变形,发动机及其挂架运动与机翼连接处保持一致。
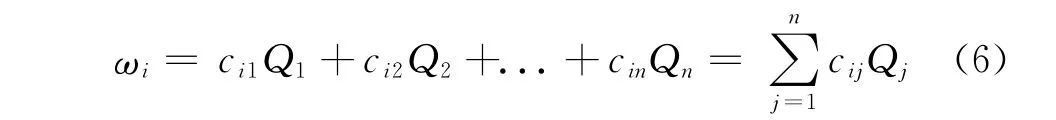
其中,i=(1,2,…,n),常数cij为柔度影响系数矩阵。则结构静力学方程为:
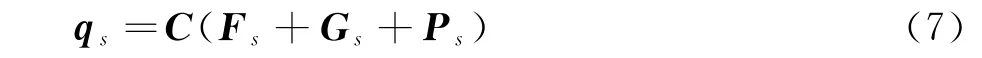
qs为结构节点在三个方向的变形位移矩阵;C为结构柔度矩阵;Fs为作用在节点上的气动力矩阵。对于型架构型逆计算来讲,只需将式(7)中力方向反向。综上所述,本文建立的静气动弹性数值模拟流程见图5。
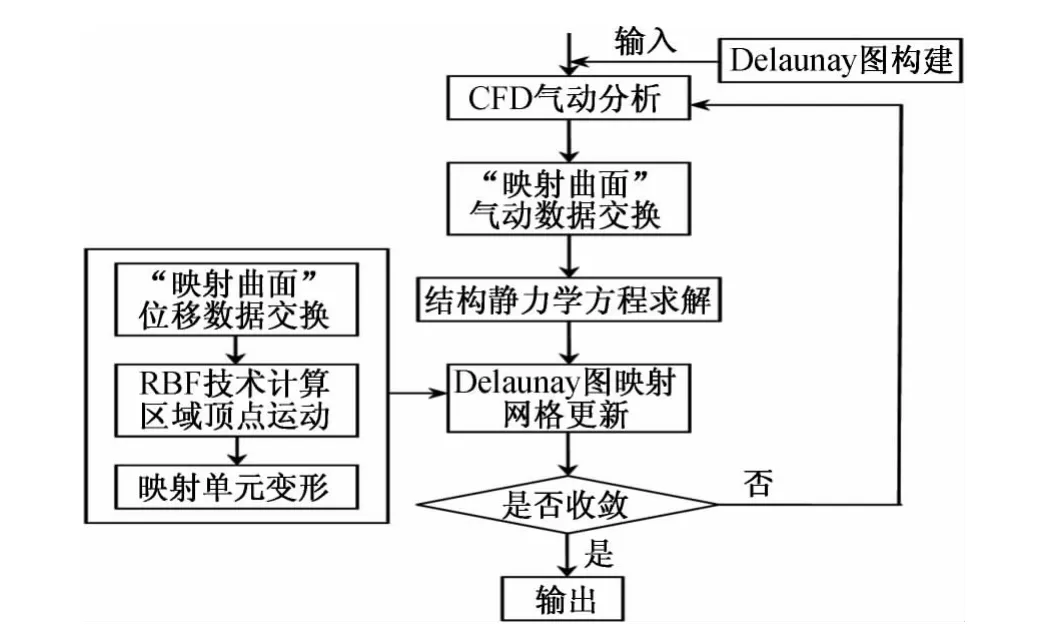
图5 静气动弹性计算流程Fig.5 Static aeroelastic work flow chart
4 某型支线客机型架外形修正与静气弹计算
以某型支线客机为型架外形为计算算例,进行型架设计后修型,进一步进行静气动弹性计算,验证所求型架构型正确性以及本文相关技术的效率、可靠性。
该型客机设计巡航状态为:
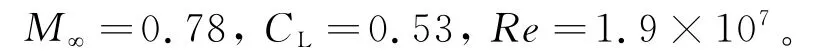
该型客机结构有限元采用杆梁单元,建立双梁单块式结构模型,主要结构元素包括前梁、后梁、翼肋等。利用有限元分析计算了该结构模型的刚度矩阵。空气动力学模型采用多区域点对接结构网格进行空间离散,空间流场流场共分为330个区域,表面划分为160个区域,共1300万个网格单元(半模)。图6给出了该支线客机的表面网格分布示意图。气动分析主控方程为Navier-Stokes方程;空间离散方法为二阶Roe格式;湍流模型采用一方程SA模型;采用LU-SGS隐式时间推进。通过线性插值的方法求出设计升力系数下所对应的巡航攻角α=1.95°。图7为巡航状态下飞机表面压力云图。
根据CFD数值模拟结果,采用文中建立的CFD/CSD共用的“映射曲面”技术进行气动载荷向结构载荷的映射,通过求解静力学方程,求出结构节点位移,再一次通过“映射曲面”技术将结构位移映射到气动网格上,从而完成型架构型的逆向计算,如图所示,绿色外形为型架构型,浅色为巡航设计外形,可以看出机翼展向下弯较为明显,表1给出了展向10个站位型架外形机翼与巡航外形的相对扭角。
对于生产与装配工艺来讲,要求机翼前缘为一直线且与巡航设计外形重合,因此在保持型架构型不变的情况下对机翼做前缘一致性修正,以满足装配工艺要求。
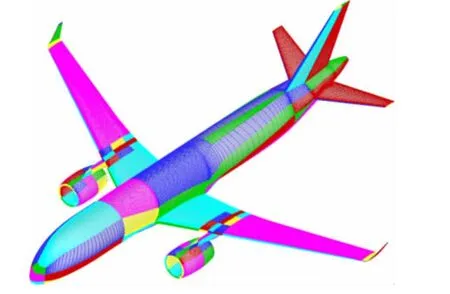
图6 CFD表面网格Fig.6 CFD surface grid

图7 巡航状态表面压力云图Fig.7 Pressure contour of cruise shape

表1 不同展向位置的机翼相对扭角Table 1 Relative torsional angles of the wing at different spanwise sections
利用文中建立的相关技术对型架外形进行静气弹计算,本文主要验证了型架构型在巡航状态下气动特性。在利用稀疏表面网格节点与空间网格顶点构建Delaunay图时,Delaunay单元数为6090个,计算时间为30s,之后由稀疏表面网格节点与空间网格顶点进行映射单元变形。本文采用以上方法既避免了Delaunay单元构建输入点的复杂操作,又从很大程度上降低了RBF大型矩阵的求解量,从而大幅度提高网格变形效率。表2给出了相同网格条件下(以DLR-F6翼身组合体为对象),不同变形网格技术与本文方法工作效率的对比,可以看出本文提出的新型变形网格方法具备较高的网格更新速度。图10给出了经过静气动弹性计算后不同网格区域顶点位置在RBF径向基函数技术操作下的更新。图11进一步给出了空间顶点更新后对应Delaunay图空间截面。在该计算模型静气弹计算过程中,RBF径向基函数技术对330个不同网格区域1000个顶点的操作仅需要0.05s时间,而对于顶点更新后Delaunay图单元变形进行的空间1300万网格节点变形仅需要1.5s,可见本文构建的径向基函数与Delaunay图映射网格变形技术效率较高,比较适用于大型工程静气动弹性计算中。整个静气动弹性经过10次迭代基本收敛。图12给出了型架构型巡航外形与巡航设计外形的对比,可以看出两者基本完全重合,验证了修正方法的正确性与静气动弹性分析的可靠性与较高效率。表3给出了两者在气动特性方面的对比,两者气动特性接近,误差较小。图13~图16给出了展向典型站位压力分布对比,压力分布形态相同基本重合。
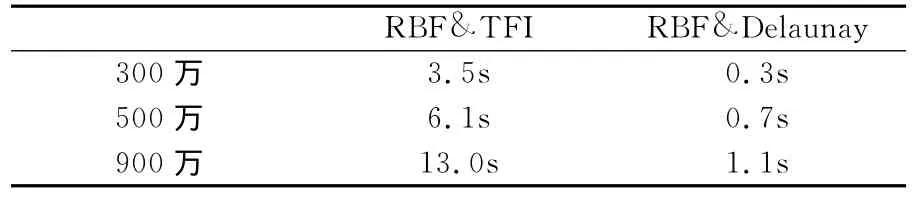
表2 不同变形网格技术效率对比Table 2 Efficient comparison between different grid deformation methods

图8 型架外形与巡航外形对比Fig.8 Jig shape and cruise shape

图9 型架外形与巡航外形局部视图Fig.9 Local view of jig shape and cruise shape
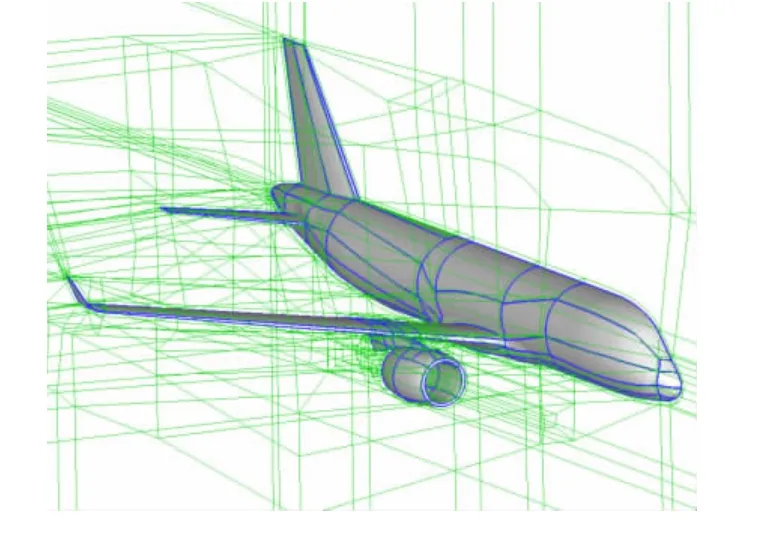
图10 RBF操作下区域顶点分布Fig.10 Block vertexs distribution under RBF operation

图11 Delaunay四面体空间截面Fig.11 Delaunay space section

图12 巡航设计外形与型架巡航外形对比Fig.12 Comparision of cruise designed shape and jig cruise shape
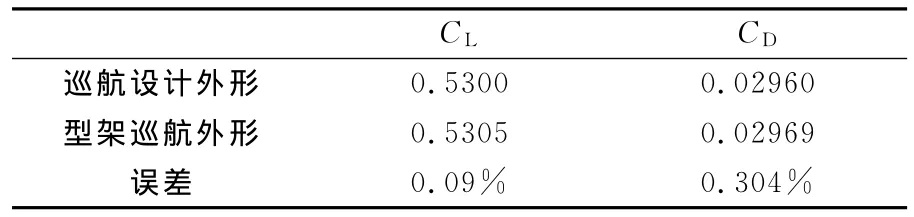
表3 巡航设计外形与型架巡航外形气动特性对比Table 3 Comparison of aerodynamic performance between cruise design shape and jig shape at cruise condition
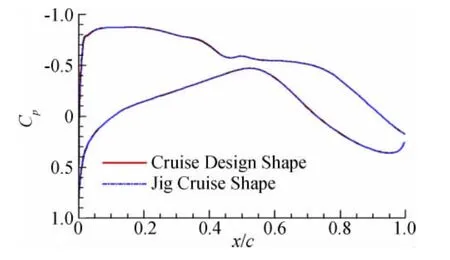
图13 y/b=0.19展向位置压力分布Fig.13 Pressure distribution of y/b=0.19spanwise section
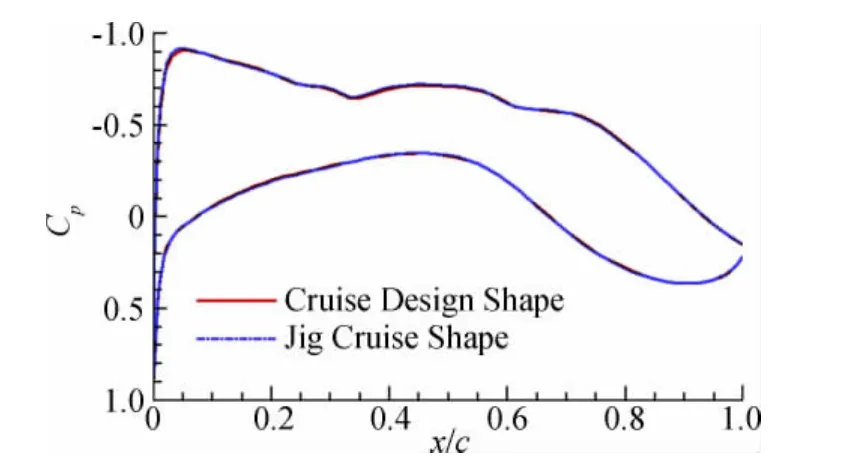
图14 y/b=0.3展向位置压力分布Fig.14 Pressure distribution of y/b=0.3spanwise section
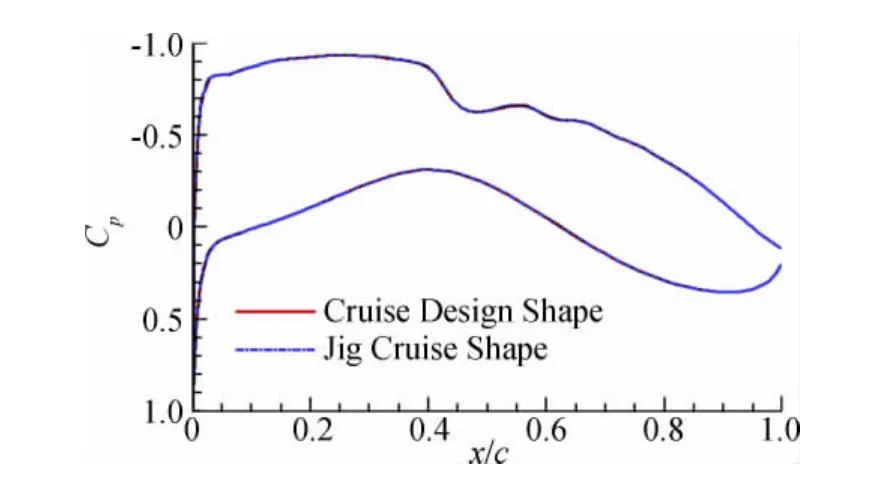
图15 y/b=0.5展向位置压力分布Fig.15 Pressure distribution of y/b=0.5spanwise section
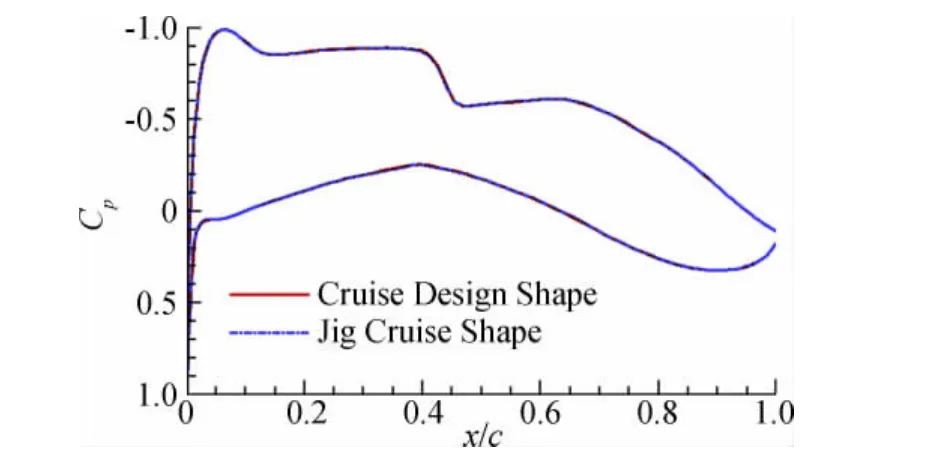
图16 y/b=0.8展向位置压力分布Fig.16 Pressure distribution of y/b=0.8spanwise section
5 结束语
本文研究了采用RBF径向基函数、Delaunay图映射技术的网格变形方法。研究建立了基于静气动弹性计算的飞行器型架外形修正设计、验证方法。对某型支线客机进行了型架外形逆推、修正及静气动弹性验证,得出如下结论:
(1)基于RBF径向基函数、Delaunay图映射的网格变形技术充分利用多块网格顶点,在避免Delaunay图单元构建时输入点的复杂操作的同时充分利用RBF对网格顶点的高效操作,与传统变形网格技术相比,计算效率较高,适应大幅度网格变形,适合于大型工程静气动弹性计算。
(2)逆推的飞行器型架构型表面光滑,变形合理,说明所采用“映射曲面”CFD/CSD数据交换技术插值精度高。
(3)通过对型架外形的气动弹性计算,验证了文中型架构型修正的正确性以及静气动弹性分析方法的可靠性、高效性。
[1]XIE C C,WU Z G,YANG C.Aeroelastic analysis of flexible large aspect ratio wing[J].Journal of Beijing University of Aeronautics and Astronautics,2003,29(12):1087-1090.(in Chinese)谢长川,吴志刚,杨超.大展弦比柔性机翼的气动弹性分析[J].北京航空航天大学学报,2003,29(12):1087-1090.
[2]GUAN D.Aeroelastic experiment[M].Beijing Aeronautics College press,1986.(in Chinese)管德.气动弹性试验[M].北京航空学院出版社,1986.
[3]YANG G W,ZHENG G N.Aircraft jig shape correction method based on static aeroelastic analyses[J].Advances in Aeronautical Science and Engineering,2011,2(2):113-150.(in Chinese)杨国伟,等.基于静气动弹性效应的飞机型架外形修正方法研究[J].航空工程进展,2011,2(2):113-150.
[4]ZHAN H,CHENG S X,ZHU J.An effective aerodynamic and aeroelastic coupled design method for complicated wing shape[J].Journal of Northwestern Polytechnical University,2009,27(1):100-104.(in Chinese)詹浩,等.考虑气动弹性影响的机翼复杂气动外形设计研究[J].西北工业大学学报,2009,27(1):100-104.
[5]ALLEN C B.Unified approach to CFD-CSD interpolation and mesh motion using radial basis functions[R].AIAA Paper 2007-3084,2007.
[6]LIU X Q,QIN N.Fast dynamic grid deformation based on Delaunay graph mapping[J].Journal of Computational Physics,2006,211:405-423.
[7]BUHMANN M.Radial basis functions[M].Cambridge University Press,2005.
[8]CIZMAS P,GARGOLOFF J.Mesh generation and deformation algorithm for aeroelasticity simulations[R].AIAA 2007-556.45th Aerospace Sciences Meeting[C].Reno,NV,2007.
[9]PARK J,SANDBERG I W.Universal approximation using radialbasis-function networks[J].Neural Computation,1991.
[10]LIGHT W A.Some aspects of radial basis function approximation.approximation theory,spline functions and applications[J].NATO ASI Series,1992,356:163-190.
[11]KARIM A,ADELI H.Radial basis function neural network for work zone capacity and queue estimation[J].J.Transp.Eng.,2003,129(5):494-503.
[12]ZHANG X,SONG K Z,LU M W,et al.Meshless methods based on collocation with radial basis functions[J].Computational Mechanics,26(4):333-343.
[13]SARLER B.A radial basis function collocation approach in computational fluid dynamics[J].CMES,2005,7(2):185-193.
[14]WENDLAND H.Fast evaluation of radial basis functions:Methods based on partition of Unity[M]//Approximation Theory X:Wavelets,Splines,and Applications.Nashville,Texas,USA:Vanderbilt University Press,2002:473-483.
[15]LI L Z.Turbine blade temperature transfer using the load surface method[J].Computer Aided Design,2007,39:494-505.
[16]ZHU X X.Free curves and surfaces modeling technology[M].Science Press,2000.(in Chinese)朱心雄.自由曲线曲面造型技术[M].科学出版社,2000.
[17]ZHAO Y H.Aeroelastic dynamics and control[M].Science Press,2007.(in Chinese)赵永辉.气动弹性力学与控制[M].科学出版社,2007.
[18]SHEN K Y,GUAN D.The principle of elastic mechanics[M].Shanghai science and Technology Press,1982.(in Chinese)沈克扬,管德.弹性力学原理[M].上海科学技术文献出版社,1982.

