开缝圆柱近场尾流的大涡模拟和实验测量

杨锦文，何 意，鲍 锋

（厦门大学 航空系，厦门 361005）

0 引 言

流体流经圆柱时可能会产生流动分离、旋涡的生成和脱落以及涡对之间的相互干扰等复杂的流动现象，虽然人们对其进行了大量的研究，但是对于该流动现象物理本质的理解仍不完整，圆柱绕流仍然是流体力学中有挑战的课题［1－2］。圆柱绕流作为流体力学研究中的经典问题之一，在化工、土木建筑、航空、水利和海洋等众多的工程领域都有非常重大的研究意义，例如化工工程中的气流经过冷凝器排管、风掠过建筑物、航空工程中的气流绕经空中加油机油管、河水对桥墩的冲击、海水流过海底输油管道等都属于典型的圆柱绕流问题。对基础圆柱进行如下图1所示的开缝修形，由于缝隙的存在会对圆柱体前后压力差产生影响，从而影响圆柱绕流的阻力和旋涡脱落涡分离频率等，对开缝圆柱的基础研究在流动减阻和流量测量等实际问题中具有广泛的应用前景。

国内外学者通过实验和数值模拟的方法对圆柱绕流进行了大量的研究，然而对经过开缝修形圆柱的研究相对较少。日本横须贺国防研究院Tamotsu Igarashi教授利用直径为34mm、缝宽比s／d为0.08和0.185的开缝圆柱，在1.38×104≤Re≤5.2×104雷诺数情况下进行了实验研究，探讨了在不同的缝隙、倾斜角β情况下开缝圆柱的流动形态，并发现在当80°≤β≤90°时，开缝圆柱阻力大于基准圆柱［3］。在后续的实验研究中进一步探讨了β＝90°时在不同的缝宽比条件下，开缝圆柱雷诺数对斯特劳哈尔数的影响［4］，发现在4.4×103≤Re≤6.5×104情况下，s／d≥0.076时，开缝圆柱的斯特劳哈尔数高于基准圆柱。J F Olsen［5］利用7种外形的圆柱进行试验比较，明确指出β＝90°时，开缝圆柱在60＜Re＜1000范围内脱体分离涡频率高于基准圆柱。鲍锋、苗君易［6］等人在水洞和风洞中，对β＝90°、s／d在0～0.3之间的开缝圆柱进行了大量的实验研究，实验结果表明当s／d在0.1～0.15之间时开缝圆柱旋涡脱落信号强于基准圆柱，而且斯特劳哈尔数随雷诺数增加的线性误差最小，利用这一原理可以提高涡街流量计的测量精度。黄咏梅、王慧［7］在管道中对开缝圆柱和梯形涡街发生体的涡街流量计进行了测量，结果表明开缝圆柱作为涡街发生体信号更强、信噪比高、测量范围广，而且斯特劳哈尔数线性度更好。Izutsu［8］和王晋军、李秋胜等［9］的实验研究表明，开缝圆柱缝隙倾斜角在一定范围时，开缝能够起到减小流动阻力的作用。

图1 开缝圆柱图形和相关参数符号Fig.1 Relative parameter symbols and sketch of circular cylinder with slit

上述工作中主要通过实验测量的手段对开缝圆柱进行研究，随着计算机性能的不断提高和计算流体力学的发展，数值模拟的方法得到了越来越广泛的运用。国内外学者对经典的圆柱绕流问题进行了大量的数值模拟，研究表明，采用大涡模拟（Large eddy simulation）的方式进行三维数值模拟的结果与实验结果符合得比较好，而且能够对高雷诺数下的圆柱绕流进行非常方便和准确的研究［10－12］。然而对开缝圆柱绕流数值模拟方面的基础研究比较少，文献［13］中利用Fluent软件模拟了开缝圆柱的二维尾流特性，并且与实验数据符合得较好。杨智春、党会学［14］对带开缝旋转圆筒固定小翼构成的飞机颤振激励器的气动特性进行了数值模拟；申春赟、杨茉［15］等采用SIMPLE方法对开缝圆柱不同开缝角度的对流换热进了数值模拟。但对于开缝圆柱绕流流场细节及其对周期性影响的三维数值模拟研究少有报导。

本文中基于Fluent软件平台采用LES的方法模拟了缝隙宽度s＝6mm、直径d＝40mm的开缝圆柱在5组雷诺数（Re＝1500、3000、4400、5837、7200）工况下旋涡脱落分离频率的变化，并对开缝圆柱后卡门涡街的形成过程以及缝隙内部流动情况进行了细致的研究。通过与厦门大学航空流体＆PIV实验室（FMPL）的定向流动显示和定量PIV实验研究［16］以及国内外相关实验数据相比较，计算的结果与实验符合得很好。对开缝圆柱内部缝隙流动和尾迹结构的精细研究和定量测量揭示了开缝对圆柱绕流流场和卡门涡街周期性的影响。开缝圆柱相对于基准圆柱其尾迹结构和周期性均有较大的变化，利用这一特性在流量测量、震颤激励、对流换热等多个工程领域有较高的应用价值。

1 数值模拟模型

1.1 大涡模拟控制方程及亚格子模型

目前，对湍流的数值模拟方法主要有：直接数值模拟（DNS），大涡数值模拟（LES）和雷诺平均模拟（RANS）。结合已有的硬件条件和研究的精度要求，以及参考近期圆柱绕流数值模拟的相关研究，大涡模拟能够在相对于DNS较小计算量的情况下较为准确的模拟整个流动的动态特性，因此选择大涡模拟。

将N－S方程无量纲化并进行过滤运算，可以得到如下的大涡模拟方程：

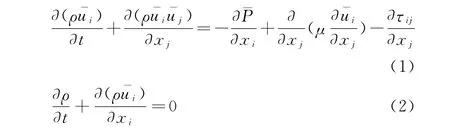
其中τij为亚格子尺度应力，其具体的数学表达如下：

亚格子应力是可解尺度脉动和过滤掉的小尺度脉动间的动量输运，需要用模型予以封闭［17］。Fluent中常用的大涡模拟封闭模式包括Smagorinsky－Lilly 模 式、Kinetic－Energy Transport动 力 模 式、WALE模式和Smagorinsky－Lilly动力模式。根据文献［18－20］中关于圆柱绕流大涡模拟的经验以及文献［17］中的相关理论表明Smagorinsky－Lilly动力模式相对于其他模式能更为准确的模拟圆柱绕流，但计算量较经典Smagorinsky－Lilly模型大30%左右。本文中采用Smagorinsky－Lilly动力模式进行计算，具体的数学表达式可见Fluent帮助文档。在数值离散格式方面，选取中心差分格式，其离散精度为二阶精度，由于网格量比较大，压力计算采用Standard模式。

1.2 几何模型及边界条件

三维开缝圆柱模型的直径d＝40mm，缝隙宽度s＝6mm。几何模型中坐标原点为圆柱圆心位置，坐标轴X方向与来流方向一致，Y方向与圆柱截面平行，Z方向是圆柱轴向，计算域上下截面关于圆柱对称，距离圆柱轴心5d，前端面距离轴心5d，后端面距离轴心15d，圆柱轴向长度为4d，具体X－Y截面尺寸如图2所示。

图2 计算模型X－Y截面尺寸示意图Fig.2 Computational model in X－Y plane

计算中采用Gambit作为网格划分工具，采取分块的六面体结构化网格划分方式，由于需要对缝隙内部流动进行观察研究，对模型进行网格划分时，进行了局部网格加密，划分的网格总数为261.6万，具体的三维网格情况如图3所示。

图3 三维模型的分块网格Fig.3 Blocked grid of the 3－D model

对于边界条件的设置，取入口为速度入口，速度大小和方向与实验来流情况相同，湍流度取1%，出口边界条件为流出出口，对应的出口压力为标准大气压，上下面和左右面为滑移壁面，滑移的速度的大小和方向与来流速度相同，开缝圆柱边界则为无滑移的壁面边界。选取的流动介质为液态水，基本参数为密ρ＝998.2kg／m3，动力粘性系数μ＝0.001003Pa·s。

2 实验模型

本文实验研究在厦门大学航空流体＆PIV实验室（FMPL）的多功能流体力学实验平台上进行，该实验平台试验段矩形截面为500mm×585mm，试验段长度为3000mm，实验设备如图4所示。经过实验前对水槽的标定和测量，循环水槽的湍流度小于1%，能够较为精密的进行开缝圆柱实验研究。

本段文字，结论句是上文的一种小结，显然，这样的结论句是水到渠成的小结，而不是可有可无的“蛇足”。第二句是论据句，举了鲍叔牙式朋友的例子，第三句至第五句分析了“真正的朋友”应当是怎样的状态，第六句（结论句）则在此基础上分析“真正的朋友”对于你的重要意义。

图4 多功能精密循环水槽Fig.4 Multifunctional precise circulating water channel

文中选取了直径d＝40mm，开缝宽度s＝6mm，s／d＝0.15的开缝圆柱和直径d＝40mm的基准圆柱进行了定性的流动显示和定量的PIV（Particle Image Velocimetry）实验研究，开缝圆柱和基准圆柱模型见图5，开缝圆柱具体尺寸参数见表1。

PIV技术是一种非侵入式的光学速度测量技术，主要通过在流体中散布大量跟随流体的示踪粒子，当示踪粒子跟随流体流经被激光片光源照亮的流场平面时被连续曝光两次，通过高速相机将被照亮的粒子记录起来，并通过图像相关性或者数位分析处理得到整个流场平面的速度矢量图。PIV技术就是通过测量示踪粒子的瞬时平均速度实现对二维流场的测量［21］。文中PIV系统的示踪粒子、高速相机和分析软件均由Dantec公司提供，示踪粒子采用聚酰胺示踪粒子PSP（Polyamid Seeding Particles），粒子直径为20μm，比较适合于水槽中的PIV测量；相机方面采用分辨率为200万像素的CMOS高速相机，可在1～1000Hz范围内调节曝光频率；软件方面采用DynamicStudio软件进行互相关分析；整套PIV系统的测量误差为1%左右，能够较为准确的计算速度场、涡量云图、流线图等。

图5 开缝圆柱及基准圆柱实验模型Fig.5 Experimental models of the slotted circular cylinder and baseline circular cylinder

表1 开缝圆柱尺寸参数Table 1 Geometrical parameters of slotted circular cylinder

3 结果与分析

3.1 开缝圆柱内部缝隙流动

对于s／d＝0.15的开缝圆柱绕流，既进行了大涡数值模拟又进行了相同尺寸情况下的流动显示和精确的PIV测量实验，下面将结合实验和数值模拟的数据，对Re＝5837的情况下开缝圆柱内部缝隙流动进行细致的研究，具体的开缝圆柱缝隙内流动的周期性演化过程如图6所示。

图6是开缝圆柱近壁面和缝隙流动一个周期的演化过程，左侧为Re＝5837情况下用PIV实测的速度矢量图，右侧为相同雷诺数情况下用大涡模拟计算的速度矢量图。经PIV试验测得此情况下开缝圆柱旋涡脱落分离频率为0.8678Hz，而数值模拟的相应值为0.8889Hz。由上述速度矢量图和脱体涡分离频率的比较可见大涡数值模拟与PIV实验符合得非常好，这充分说明了大涡模拟的准确性。

图6 PIV与数值模拟速度矢量图Fig.6 PIV experiments and computational simulations velocity vector diagrams

通过对整个流动周期进行分析可知，在t＝0或者t＝T时刻，开缝圆柱上方的水流被“吸进”缝隙，缝隙下方的流体被“吹出”缝隙，靠近圆柱后壁面下部有逆时针旋转的小涡；当t＝1／4T 时，上方流体不断进入缝隙后，在缝隙上半部分形成两个小涡，其旋转方向由上至下依次为顺时针和逆时针，紧贴壁面的小涡经发展积累变强并向下游脱落；当t＝2／4T时，缝隙内下方的流体速度降至最低值后，经过短暂的“过渡阶段”开始进入下半周期，此时水流从下方缝隙被“吸进”缝隙，并从上方“吹出”，紧靠圆柱后壁面上部有小涡；在t＝3／4T时，则水流从下方不断进入缝隙后，在下方形成两个不同方向旋转的小涡，方向由下往上依次为逆时针和顺时针，紧靠圆柱后壁面上部的小涡动态的增强发展成为大涡后脱落；上述流动演化过程依次往复周期性的进行，在圆柱缝隙内部形成了周期性上下震荡［22］。缝隙中流体周期性的震荡导致了开缝圆柱近壁面区边界层的“吸入”和“吹出”效应，根本上改变了近区尾流的结构。

3.2 开缝圆柱缝近壁面流动及卡门涡街研究

当圆柱体以一定的速度在静止的水中运动或者圆柱静止不动，流体以一定速度流向圆柱时，在一定雷诺数下会产生交替的卡门涡街。本文中大涡数值模拟与PIV实验研究的数据符合得比较好，且数值模拟的速度矢量图能够更加明确的显示流动细节，文中以雷诺数Re＝5837、缝宽比s／d＝0.15的数值模拟情况对开缝圆柱近壁面流动情况和卡门涡街的形成过程进行阐述，其具体的近壁面速度矢量图和二维涡量图如图7、图8所示。

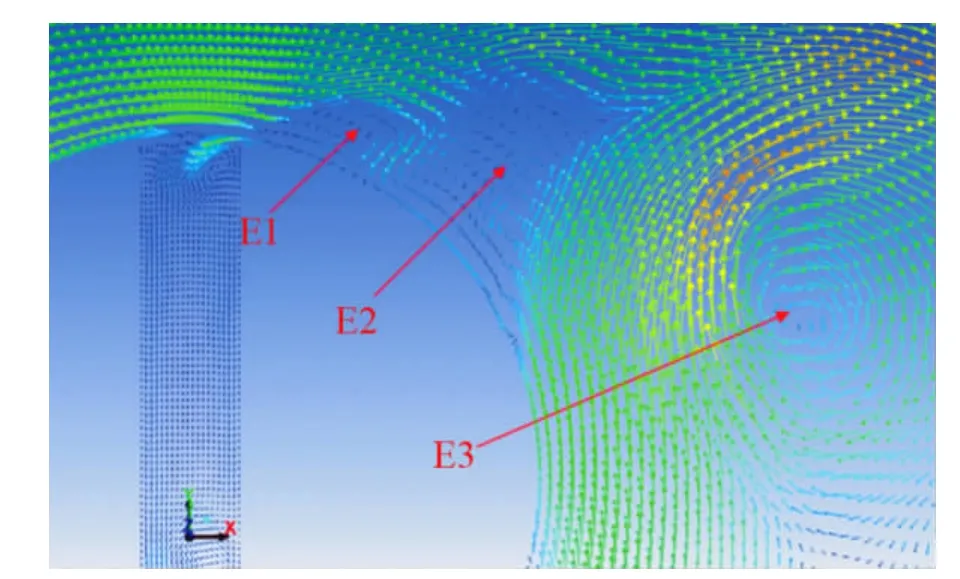
图7 开缝圆柱壁面附近速度矢量图Fig.7 Velocity vector diagram near the wall of the slotted circular cylinder

图8 Z＝2d平面涡量云图Fig.8 Vorticity contour for section Z＝2d

当流体流经圆柱表面时，圆柱后部上表面由于逆压梯度，边界层发生分离，并伴随着流体流动的作用生成主涡E3，由于流体质点的相互作用诱导临近部分生成的二次涡E2将主涡分割成E3和E1两部分，随着E2的发展，E1逐渐增强，并将E3排至下游区域，随后E2开始萎缩变形，然后E1重新与主涡相连接。随着时间的推移，涡E1部分地耗散，二次涡E2重新增大，至此完成一个周期的涡街形成与脱落。一个周期后，E1又将逐渐增大，并且附着于圆柱后壁面，E2则处于剪切层的上方，随着E1的增强和发展，主涡E3在自身诱导作用和背景流场的作用下向下游脱落，形成尾迹边界。整个过程中二次涡交替的与主尾迹和外流相互作用，当二次涡与外流联通时，将引起主涡的分割和脱落，如此往复，形成不稳定的涡街。

3.3 开缝圆柱三维特性分析

对开缝圆柱进行三维数值模拟，导出的涡量云图如下图9所示，从中可以清楚的看到开缝圆柱尾部产生了很多扭曲的涡管，其运动远比二维旋涡运动复杂，其主要原因是三维曲线涡上的每一点都受到该涡线自身的诱导作用即自诱导作用，在自诱导作用下，涡管形状随时间不断变化。开缝圆柱近壁面区域存在较大的剪切力，涡管远离壁面部分比靠近壁面部分传递得快，近壁面涡管在强剪切力的作用下很快被拉伸且伸长，形成了平行于来流方向的涡对，由于圆柱壁面是无滑移的速度边界条件，圆柱壁面附近在逆压梯度和背景流场的作用下发生了扰动，形成复杂的次生流动现象。

开缝圆柱尾流区存在着各种大小不同的旋涡结构，整个流场的特性都取决于这些旋涡的不断产生、发展和消散，同时，这些旋涡之间又不断发生着复杂的相互作用。整个过程中，在涡丝和涡管自诱导和背景流场的相互作用下，沿着涡丝的微小扰动随时间的推移得到了持续的放大，并且使得涡量在空间重新分布，出现了复杂的三维流向涡结构。

图9 开缝圆柱涡量云图Fig.9 Vorticity contour of slotted cylinder

3.4 圆柱开缝的影响探讨

3.4.1 开缝与基准圆柱近场尾迹的比较

本文同时选取了直径d＝40mm的基准圆柱和直径d＝40mm，s／d＝0.15的开缝圆柱在0＜Re≤7200范围内进行定性的流动显示实验和定量的PIV测量，探讨了β＝90°情况下开缝圆柱和基准圆柱尾迹以及脱体涡频率的不同。下面仅取Re＝5837情况下，开缝圆柱和基准圆柱的尾迹情况进行分析，其一个周期内的尾迹发展情况如下图10所示。

图10中左侧蓝色圆柱和右侧红色圆柱分别为基准圆柱和开缝圆柱近场尾迹演化图。由此可见在实验雷诺数0＜Re≤7200和缝隙倾斜角β＝90°情况下，开缝圆柱与基准圆柱尾迹的结构特征基本相似，圆柱后都呈现出周期性的“卡门涡街”现象，但是对于基准圆柱，其近场尾流区域速度分布较为凌乱，卡门涡街主涡分离点距离圆柱较远，而开缝圆柱的近场尾迹较为规整，卡门涡街主涡分离点距离圆柱更近，卡门涡街现象更加明显。上述现象说明在β＝90°情况下开缝圆柱缝隙内部流体周期性的震荡加强了圆柱绕流的尾流脉动，使得圆柱绕流近场尾迹增强，周期性的“卡门涡街”现象更加明显。

3.4.2 开缝与基准圆柱周期性研究

本文的实验从定量角度出发，测量比较了开缝圆柱与基准圆柱在不同雷诺数下的脱体涡频率，并将大涡模拟监测计算的脱体涡频率与之对比，发现计算与实验值符合得很好，两者的误差在5%以内。实验和计算的结果表明，基准圆柱和开缝圆柱的旋涡脱落频率都随雷诺数的增大而呈现出近似线性的增大，但是在文中的缝宽比和雷诺数范围内，开缝圆柱的旋涡脱落频率高于相同雷诺数情况下的基准圆柱，在3700≤Re≤7200范围之内，开缝圆柱脱体涡频率较基准圆柱高15%左右。具体的基准圆柱与开缝圆柱的脱体涡频率比较如图11所示。

斯特劳哈尔数St是当地惯性力与迁移惯性力的比值，它反映流动非定常运动的相似性，对于周期性的非定常运动就反映其周期性相似，所以和周期性相关的非定常流动由St决定［23］。文中实验和数值模拟采用式（4）计算斯特劳哈尔数，其中f为旋涡脱落频率，d为圆柱直径，V0为来流速度。

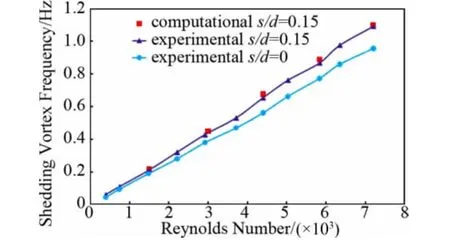
图11 开缝圆柱与基准圆柱旋涡脱落分离频率Fig.11 Vortex shedding frequency of baseline circular cylinder and slotted one

Roshko［24］在对圆柱绕流进行了大量实验研究的基础上提出了Re＞300的St计算经验公式（5），文中Roshko数据采用公式（5）进行计算。

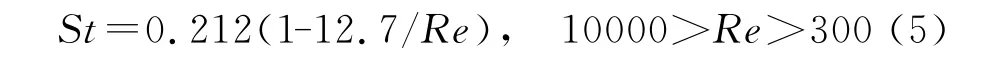
将本文中PIV实验和数值模拟结果计算的St数与Roshko的经验公式计算数据以及文献［6］中的PIV实验测量值相对比，具体如图12、图13所示，两者符合得较好。

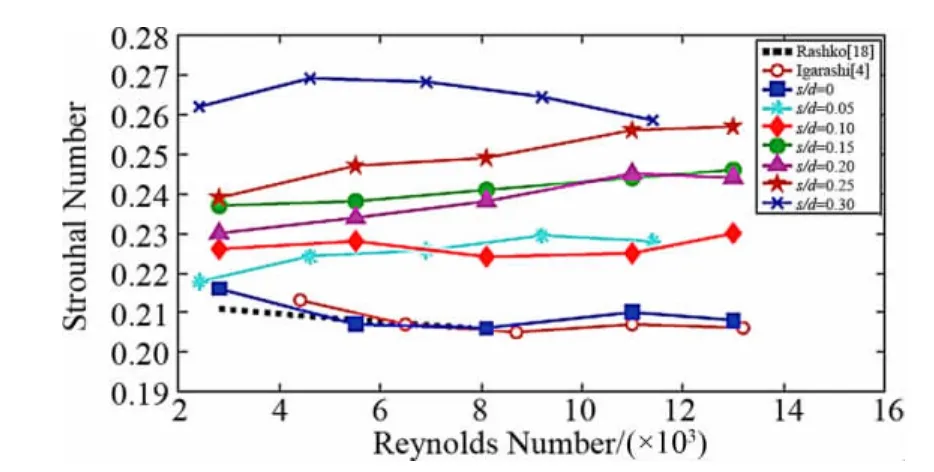
图12 实测的斯特劳哈尔数［6］Fig.12 Experimental results of Stouhal number［6］

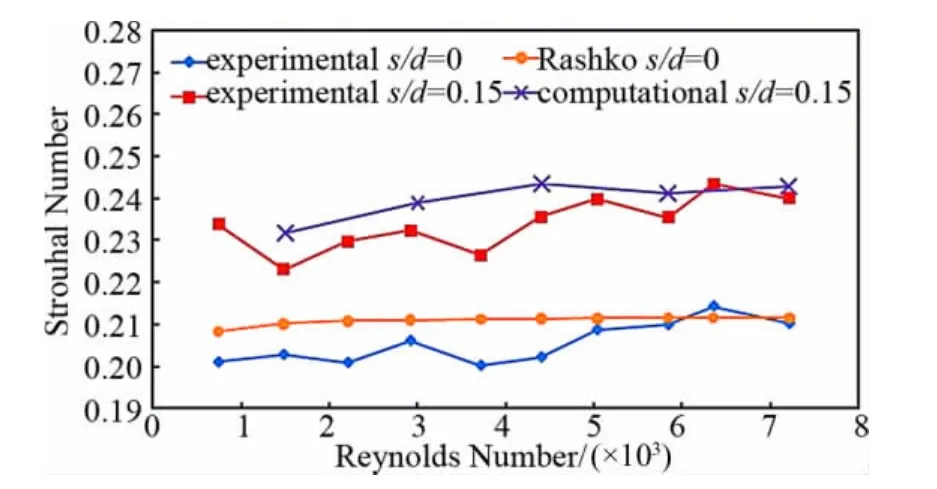
图13 实验和计算的斯特劳哈尔数Fig.13 Experimental and computational results of Stouhal number

实验和计算结果表明，在1500≤Re≤7200范围内，基准圆柱的St数稳定在0.2～0.21之间，而开缝圆柱的St数要明显的高于基准圆柱，其实验值在0.223～0.245之间。文献［6］中的测量数据表明在2400≤Re≤11400范围内，s／d＝0.15的开缝圆柱实时的斯特劳哈尔数频率谱特性较s／d＝0的基准圆柱更好，其St数与Re数的线性相关性在0≤s／d≤0.3范围内最好，利用这一现象可以提高涡街流量计的测量精度。

4 结 论

本文采用大涡模拟（LES）的方法对直径d＝40mm、缝宽比s／d＝0.15的开缝圆柱在五种不同雷诺数（Re＝1500、3000、4400、5837、7200）情况下的近场尾迹进行了研究，并结合基准圆柱与相同缝宽比时的开缝圆柱实验研究得出以下结论：

（1）缝隙倾斜角β＝90°时，实验和计算的雷诺数范围内，流体流经开缝圆柱时，在圆柱缝隙内部形成了类似于“活塞”的流动现象，即流体上下周期性地震荡，这种震荡导致了近壁面区边界层的“吸入”和“吹出”效应，从根本上改变了圆柱绕流近区尾流的结构。

（2）对开缝圆柱卡门涡街的形成过程和涡量图的分析表明开缝圆柱涡管呈现出复杂的运动，整个尾迹流动呈现出明显的三维流动特点。

（3）对开缝圆柱与基准圆柱近场尾迹研究比较表明，圆柱缝隙内部周期性的震荡增强了圆柱后尾迹的脉动，开缝圆柱近场尾迹的“卡门涡街”现象更加明显和规整。

（4）在缝隙倾斜角β＝90°、s／d＝0.15情况下，开缝圆柱的旋涡脱落分离频率和斯特劳哈尔数高于相同雷诺数情况下的基准圆柱，在3700≤Re≤7200范围内，开缝圆柱的旋涡脱落分离频率高于基准圆柱15%左右，缝隙对开缝圆柱表面的压力和表面作用力分布产生了重要影响。

［1］WILLIAMSON C H K.Vortex dynamics in the cylinder wake［J］.Annual Review of Fluid Mechanics，1996，28：477－539.

［2］ROUSHAN P，WU X L.Universal wake stuctures of Kármán vortex steets in two－dimensional flows［J］.Physics of Fluids，2005，17：073601.

［3］TAMOTSU IGARASHI.Flow characteristics around a circular cylinder with a slit：1st report，flow control and flow patterns［J］.Bulletin of the JSME，1978，21（154）：656－664.

［4］TAMOTSU IGARASHI.Flow characteristics around a circular cylinder with a slit：2nd report，effect of boundary layer flow［J］.Bulletin of the JSME，1982，25（207）：1389－1397.

［5］OLSEN J F，RAJAGOPALAN S.Vortex shedding behind modified circular cylinders［J］.Journal of Wind Engineering ＆ InduS－tial Aerodynamics，2000：55－63.

［6］PENG B H，MIAU J J，BAO F，et al.Performance of vortex shedding from a circular cylinder with a slit normal to the Steam［J］.Flow Measurement and Instumentation，2012，25：54－62.

［7］WANG H，HUANG Y M.Study of flow rate measurement characteristics of a circular cylinder with a slit［J］.Chinese Journal of Sensors and Actuators，2013（12）：1661－1665.（in Chinese）王慧，黄咏梅.带狭缝圆柱钝体流量测量特性研究［J］.传感技术学报，2013（12）：1661－1665.

［8］IZUT Su N.Fluid force measurements for a circular cylinder with a slit［J］.Nagare，1993，12：293－301.

［9］TAN G K，WANG J J，LI Q S.Drag reduction technique of cylinder and mechanism research［J］.Journal of Beijing University of Aeronautics and Astronautics，2001，27（6）：658－661.（in Chinese）谭广琨，王晋军，李秋胜.圆柱体减阻技术及其机理初步研究［J］.北京航空航天大学学报，2001，27（6）：658－661.

［10］HAO P，LI G D，YANG L，et al.Large eddy simulation of the circular cylinder flow in different regimes［J］.Chinese Journal of Applied Mechanics，2012，29（4）：437－443.（in Chinese）郝鹏，李国栋，杨兰，等.圆柱绕流流场结构的大涡模拟研究［J］.应用力学学报，2012，29（004）：437－443.

［11］BREUER M.A challenging test case for large eddy simulation：high Reynolds number circular cylinder flow［J］.International Journal of Heat and Fluid Flow，2000，21（5）：648－654.

［12］SARKAR S，SARKAR S.Large－eddy simulation of wake and boundary layer interactions behind a circular cylinder［J］.Journal of Fluids Engineering，2009，131（9）：091201－14.

［13］BAO F，MIAU J J，LIU Z R，et al.Near－wake flow characteristics of modified cylinder with slit［C］／／The 2th Asian Symposium on Visualization.Niigata，Japan，2011：5－9.

［14］YANG Z C，DANG H X，SUN Y J，et al.Numerical simulation of the aerodynamic characteristics of a fixed wing with trailing edge rotating slotted cylinder［J］.Engineering Mechanics，2009，（011）：222－227.（in Chinese）杨智春，党会学，孙勇军，等.带开缝旋转圆筒固定小翼气动特性的数值模拟［J］.工程力学，2009，（011）：222－227.

［15］SHEN C Y，YANG M，WANG J，et al.Natural convection heat transfer characteristics of a circle with an internal concentric round slotted in different direction［J］.Journal of University of Shanghai for Science and Technology，2013，35（5）：425－429.（in Chinese）申春赟，杨茉，王津，等.圆内开缝圆不同开缝方向自然对流换热［J］.上海理工大学学报，2013，35（5）：425－429.

［16］JUNWEI W，JINWEN Y，YI H，et al.Experimental study of slit cylinder vortex shedding in circulating water channel［R］／／Measurement，Information and Control（MIC）［A］.2012International Conference on IEEE［C］.2012，1：225－229.

［17］CUI G X，XU C X，ZHANG Z S.Progress in large eddy simulation of turbulent flows［J］.ACTA Aerodynamica Sinica，2004，22（2）：121－129.（in Chinese）崔桂香，许春晓，张兆顺.湍流大涡数值模拟进展［J］.空气动力学学报，2004，22（2）：121－123

［18］JIA X H.Large eddy simulation of flow aroundone and two circular cylinders［D］.Shanghai：Shanghai Jiao Tong University，2008.（in Chinese）贾晓荷.单圆柱及双圆柱绕流的大涡模拟［D］.上海：上海交通大学，2008.

［19］JIA X H，LIU H.Large eddy simulation of flow around two circular cylinders［J］.Chinese Journal of Hydrodynamics：A，2008，23（6）：625－632.（in Chinese）贾晓荷，刘桦.双圆柱绕流的大涡模拟［J］.水动力学研究与进展：A 辑，2008，23（6）：625－632.

［20］KRAVCHENKO A G，MOIN P.Numerical studies of flow over a circular cylinder at Re＝3900［J］.Physics of Fluids，2000，12：403.

［21］LIU Y，LIANG Z S，BAO F.Particle image velocimetry－a whole fields technology with out disturbs the flow［J］.Chinese Science and Technology Information，2010，13（11）：37－40.（in Chinese）刘玥，梁忠生，鲍锋.粒子成像测速——非介入式全场技术［J］.中国科技信息，2010，13（11）：37－40.

［22］BAO F，MIAU J J，et al.Complex near－wake flow of limited and ventilated cylinders［A］.The 9th Asian Symposium on Visualization［C］.2007.

［23］WANG J M，ZHANG Z H，MA Q C.Fluid dynamics［M］.Dalian：Dalian Maritime University Press，2002.（in Chinese）王家楣，张志宏，马乾初编著.流体力学［M］.大连：大连海事大学出版社，2002.

［24］ROSHKO A.On the development of turbulent wakes from vortex steets［R］.NACA Report 1191.Washing D.C.：National Advisory Committee for Aeronautics，1954.