修正的基于广义Gamma语音模型语音增强算法
赵改华,周 彬,张雄伟
ZHAO Gaihua,ZHOU Bin,ZHANG Xiongwei
解放军理工大学 指挥信息系统学院,南京 210007
College of Command Information Systems,PLA University of Science and Technology,Nanjing 210007,China
1 引言
在语音通信过程中,语音信号不可避免地会受到噪声的干扰,影响通信质量和语音信号的后续处理,语音增强技术是从含噪语音中尽可能提取原始纯净语音的重要手段,在提高语音可懂度、改善语音通信质量等方面有重要的应用。在众多的增强技术中基于统计模型的短时谱估计法以其复杂度低和相对有效的特点,长期以来受到了广大研究者的广泛关注。
基于统计模型的短时谱估计语音增强算法,主要是在不同的语音和噪声先验分布模型假设下,依据一定的准则(如MMSE、MAP等)对语音信号的短时谱进行最优估计[1-3]。早期的算法通常假设语音信号服从高斯分布,例如,文献[1]首先提出了基于高斯模型的最小均方误差短时幅度谱估计算法(MMSE-STSA)。文献[2]考虑人耳的听觉感知机理,进一步提出了基于高斯模型的最小均方误差对数幅度谱估计算法(MMSE-LSA)。近年来对语音信号统计模型的深入研究表明,超高斯分布更符合实际的语音分布[4]。因此,文献[5-7]提出了基于超高斯语音模型的短时谱估计算法,包括基于超高斯模型的复频谱MMSE估计算法、基于超高斯模型的幅度谱最大后验概率估计算法和基于Gamma模型的DCT域MMSE估计算法,相对于传统的基于高斯模型的增强算法进一步抑制噪声并降低了语音失真度。在此基础上,研究者将上述模型进行一般化推广,提出了语音信号的广义Gamma分布模型,据此文献[8]首先将广义Gamma模型应用于语音短时谱估计,提出了基于广义Gamma语音模型的复频谱MMSE估计算法,在此基础上,文献[9]提出了基于广义Gamma语音模型的对数幅度谱估计算法,文献[10]进一步将广义Gamma语音模型与语音信号的动态特性相结合,增强效果有较大的提高。此外,考虑语音信号在各时间帧和各频带存在的不确定性,文献[3]在基于高斯模型的对数谱最小均方误差估计算法的基础上,提出了以语音存在概率作为修正因子的改进短时谱估计算法,文献[5]进而将这一方法应用于超高斯语音模型,推导了在Laplacian和Gamma模型假设下的语音存在概率,实验结果表明,语音存在概率的引入能够进一步抑制残留噪声,改进增强效果。但是这些算法仍然采用传统的高斯或超高斯语音模型,因而增强效果有限。
针对上述算法的不足,本文提出一种新的基于广义Gamma语音模型的短时谱估计算法。在假设语音和噪声的幅度谱分别服从广义Gamma分布和Gaussian分布的基础上,推导了语音信号对数谱的MMSE估计式。另外,考虑到语音信号是否存在的不确定性,进一步推导了在广义Gamma语音模型下的语音存在概率,以此对MMSE估计进行修正。实验结果表明,本文提出的算法不仅能进一步提高增强语音的信噪比,而且可以有效地抑制残留噪声,提高增强语音的感知质量。
2 传统短时谱估计算法
假设s(n)表示纯净语音信号,x(n)表示加性噪声信号,那么时域带噪语音信号可表示为 y(n)=s(n)+x(n),对时域带噪语音信号进行分帧、加窗和STFT变换,可以得到带噪语音信号在频域内的表示:

l(l=0,1,…)表示帧序号,k(k=0,1,…,k-1)表示频带序号,用幅度和相位表示:
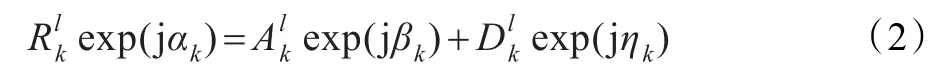
一般地,假设噪声复频域系数的实部和虚部分别服从高斯分布,则噪声幅度谱系数服从瑞利分布[3]:


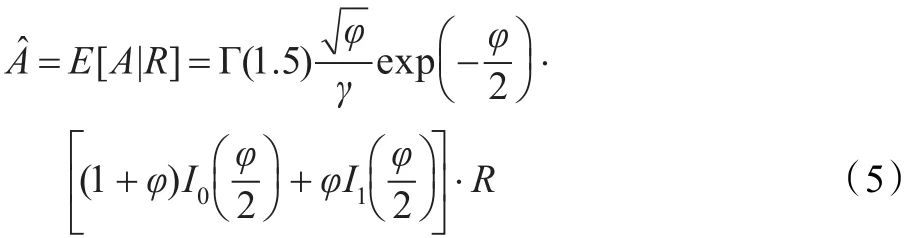
对语音信号统计模型的深入研究表明,超高斯分布更符合语音信号的统计特性,因此,许多研究者提出了基于超高斯模型的短时谱估计算法,包括基于Gamma语音模型[7]和基于Laplacian语音模型[5]的语音增强算法等。
3 基于广义Gamma模型的对数谱MMSE估计
广义Gamma模型是近年来新提出的一种语音分布模型,其相对于传统的高斯或超高斯模型具有更好的普适性和灵活性。本章在假设语音和噪声的对数谱分别服从广义Gamma分布和Gaussian分布的基础上,推导语音对数谱的MMSE估计。
在广义Gamma语音模型下,纯净语音的先验概率密度函数为[8]:
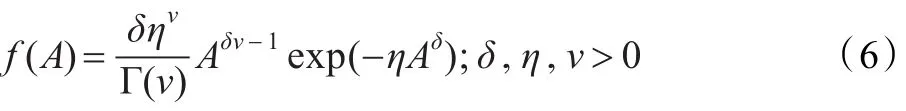
其中Γ(·)表示Gamma函数。假设噪声仍服从高斯分布,如式(3)。语音信号的对数谱估计式为[2]:
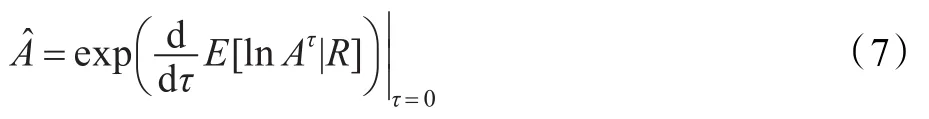
公式(7)可近似表示为:
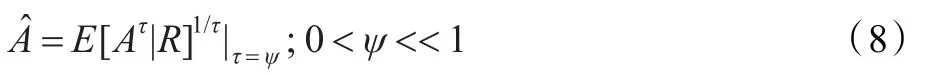
研究表明,广义Gamma分布的参数选取0<ν≤1,δ=1较为符合语音的先验分布特性[9]。取δ=1,则:
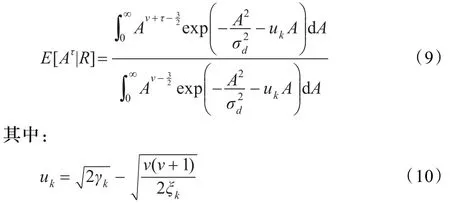
利用ν阶抛物柱面函数Dv对式(9)进行积分化简[11]:
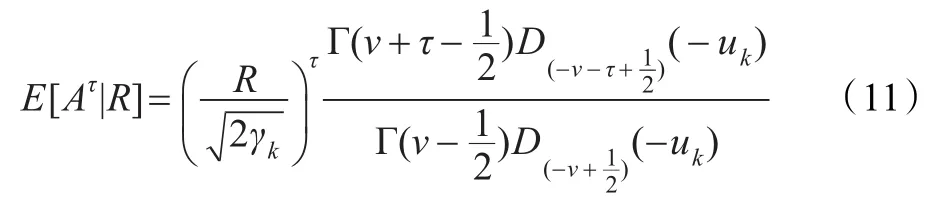
将式(11)代入式(8)即得到纯净语音的MMSE短时谱估计式:
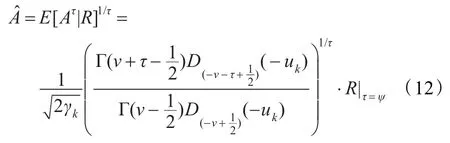
用增益函数的形式表示为:
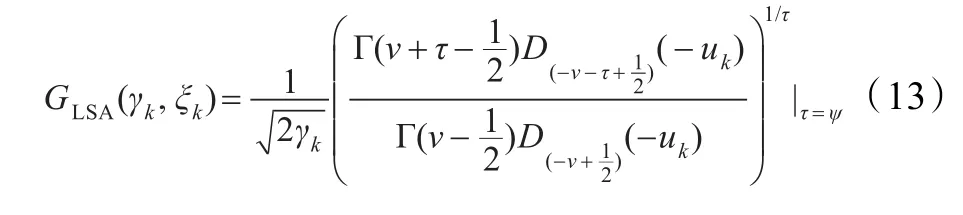
4 基于语音存在概率的谱估计修正
由于语音信号存在无语音帧,并且语音信号的能量主要集中在基音频带及其谐波频带上,因此语音信号在各时间帧和各频带的存在具有不确定性,以语音存在概率作为修正因子的改进短时谱估计算法有效地提高了增强效果[3,5]。本章在广义Gamma语音模型和Gaussian噪声模型下,推导出语音存在概率,对第3章MMSE估计进行修正。
假设H0表示不存在语音信号,H1表示存在语音信号,相应的P(H1|R)表示在给定R条件下语音存在的概率,P(H0|R)表示在给定R条件下语音不存在的概率,利用贝叶斯准则得到[3]:

则修正后的增益函数表示为[1]:
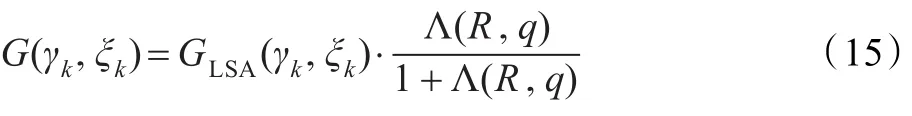
其中Λ(R,q)表示广义似然比:
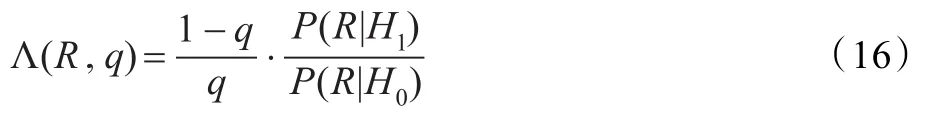
其中q表示先验语音不存在概率,P(R|H0)表示语音不存在条件下R的概率密度函数,在高斯噪声模型下有:
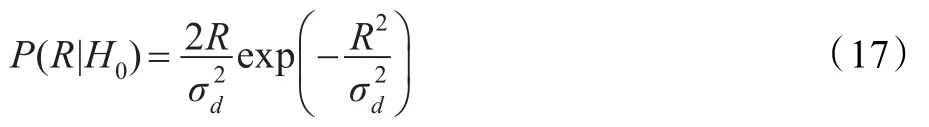
P(R|H1)表示在语音存在条件下R的概率密度函数,表示为:
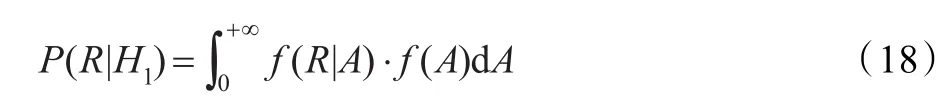
其中 f(A)表示语音信号 A的概率密度函数,f(R|A)表示在已知语音信号A的条件下带噪语音R的条件概率密度函数,在广义Gamma语音模型和Gaussian噪声模型下有:
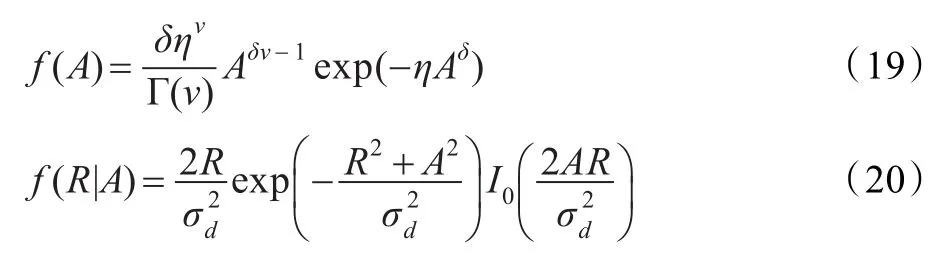

根据文献[11]中的公式,将近似式式(22)代入式(21)积分化简后即可求得语音存在条件下R的概率密度函数:
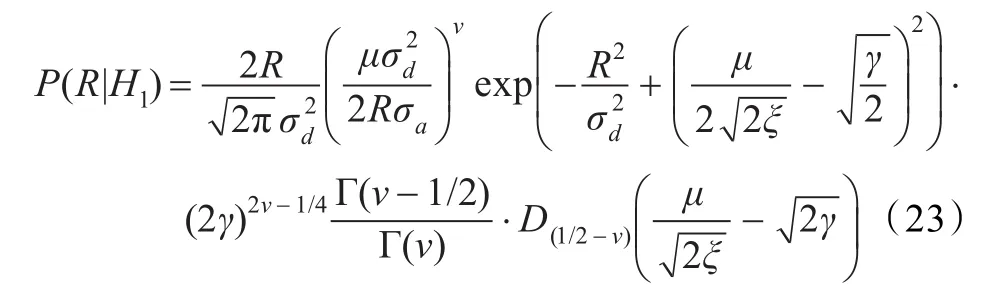
将所求得的P(R|H0)和P(R|H1)代入式(16)得广义似然比:
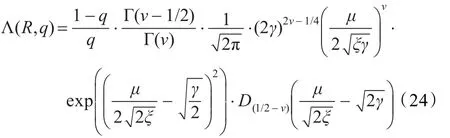
将广义似然比式(24)代入式(15)即可求得修正后的基于广义Gamma语音模型的纯净语音的对数谱MMSE估计,则语音信号的幅度谱估计为:
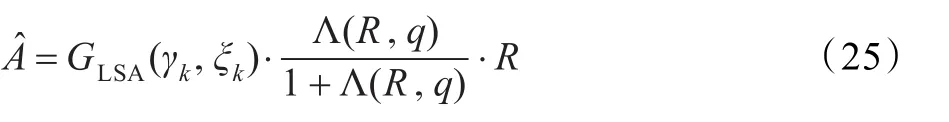
5 仿真结果
在MATLAB环境下进行仿真实验,研究表明ν=0.75能在低信噪比时更好地抑制噪声,高信噪比时保留语音信号,本文中选择ν=0.75[8-9];语音的不存在先验概率q=0.2;ψ=10-4;噪声估计采用文献[12]提出的统计最小量跟踪算法。原始噪声信号从标准噪声库Noisex92中选取,包括白噪声、M109坦克噪声以及F16飞机噪声,并下采样为8 kHz。纯净语音信号为标准汉语语音信号,采用8 kHz采样,时间长度约为8 s,男女声各8句。利用MATLAB对噪声信号和纯净语音进行混和,信噪比分别定为−5 dB、0 dB、5 dB和10 dB。
在仿真中,将本文提出的增强算法与以下三种算法进行比较,包括:文献[1]提出的基于高斯模型的MMSE短时幅度谱估计法;文献[3]提出的语音存在概率修正的对数谱MMSE估计法;文献[9]提出的基于广义Gamma语音模型的对数谱MMSE谱估计法。为简化表示,这三种算法分别表示为Gau、Gau-SPP、GGD。本文提出的算法表示为:GGD-SPP。
采用分段信噪比SegSNR(segmental SNR)、对数谱距离LSD(log spectral distance)、客观质量评估方法PESQ(Perceptual Evaluation of Speech Quality)对语音增强算法性能进行客观衡量。分段信噪比SegSNR和对数频谱距离LSD计算公式分别表示为:
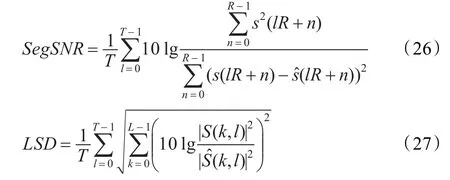
采用增强后和增强前语音分段信噪比提高量来衡量不同短时谱估计算法的噪声抑制性能。表1给出了在不同噪声和信噪比条件下分段信噪比的提高量。从表中可以看出,相较于其他三种短时谱估计算法,在给出的三种环境噪声下,本文算法增强语音的分段信噪比提高量均有所提升,说明其具有更好的噪声抑制效果。
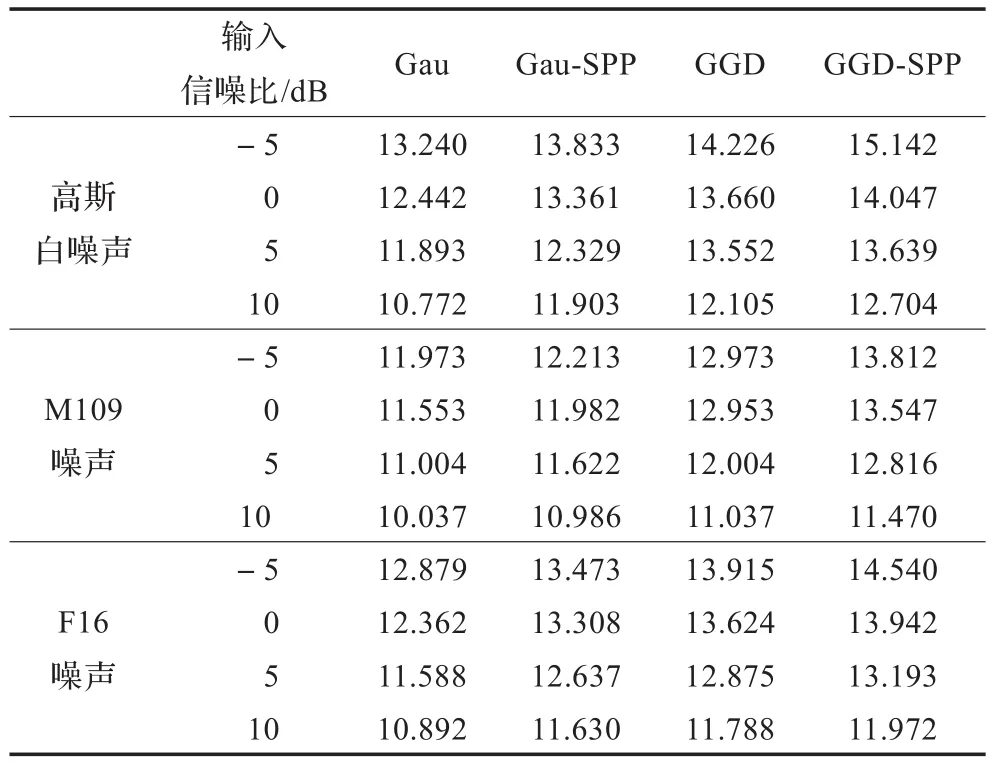
表1 四种算法的分段信噪比提高量
采用对数频谱距离LSD衡量增强语音的失真度。图1给出了在不同噪声和信噪比条件下的LSD改进曲线,从图中可以看出,相较于其他三种谱估计算法,本文提出算法的增强语音的失真度更小。比较GGD和GGD-SPP的LSD改进曲线,可以明显看出,由于语音存在概率修正的引入,本文提出算法的增强语音具有更小的失真度,增强效果有所提高。
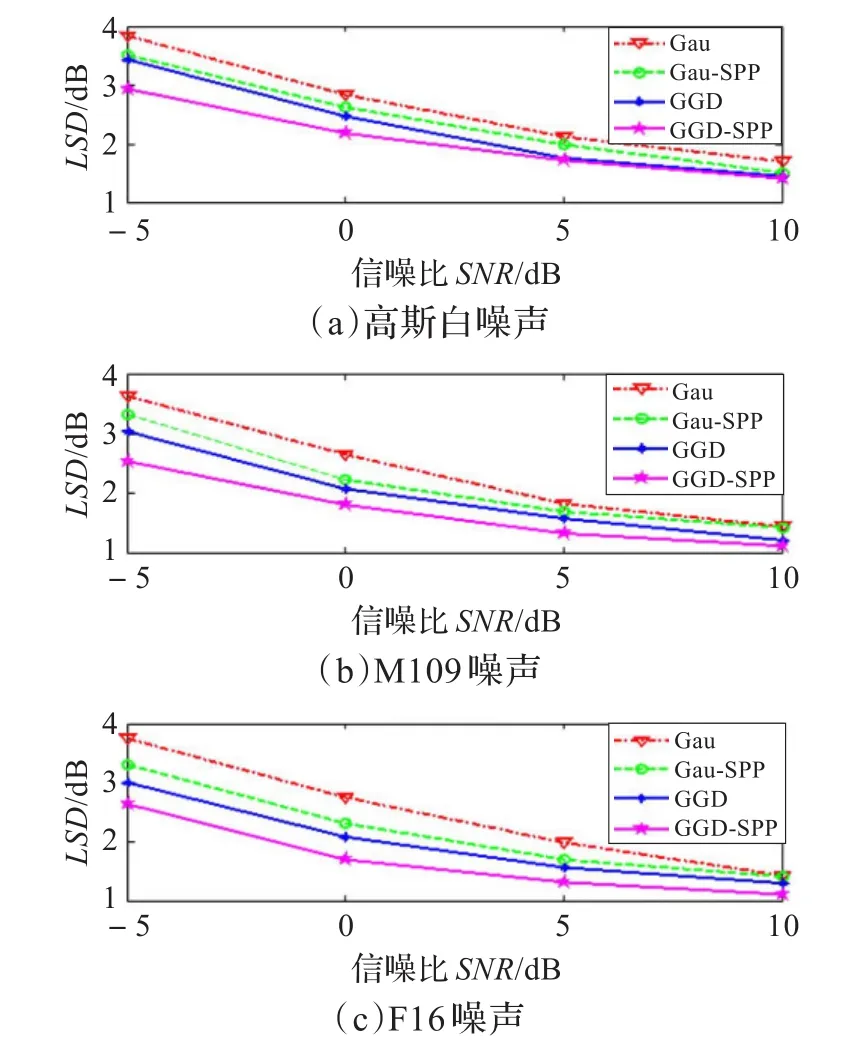
图1 对数频谱距离改进曲线
采用客观质量评估方法PESQ衡量增强语音的质量。表2给出了在不同噪声和信噪比条件下的PESQ评估结果,从表2中可以看出,在给出的三种环境噪声下,本文算法增强语音的PESQ得分都明显高于其他三种谱估计算法,说明其具有更好的感知质量。另外,比较Gau-SPP和GGD-SPP两种谱估计算法,从实验结果可以看出,虽然Gau-SPP也引入了语音存在概率修正因子,但是仍基于高斯模型,增强效果有所限制,本文提出的GGD-SPP由于采用了与语音的分布特性更为贴合的广义Gamma模型,PESQ得分要高于前者,具有更好的增强效果。
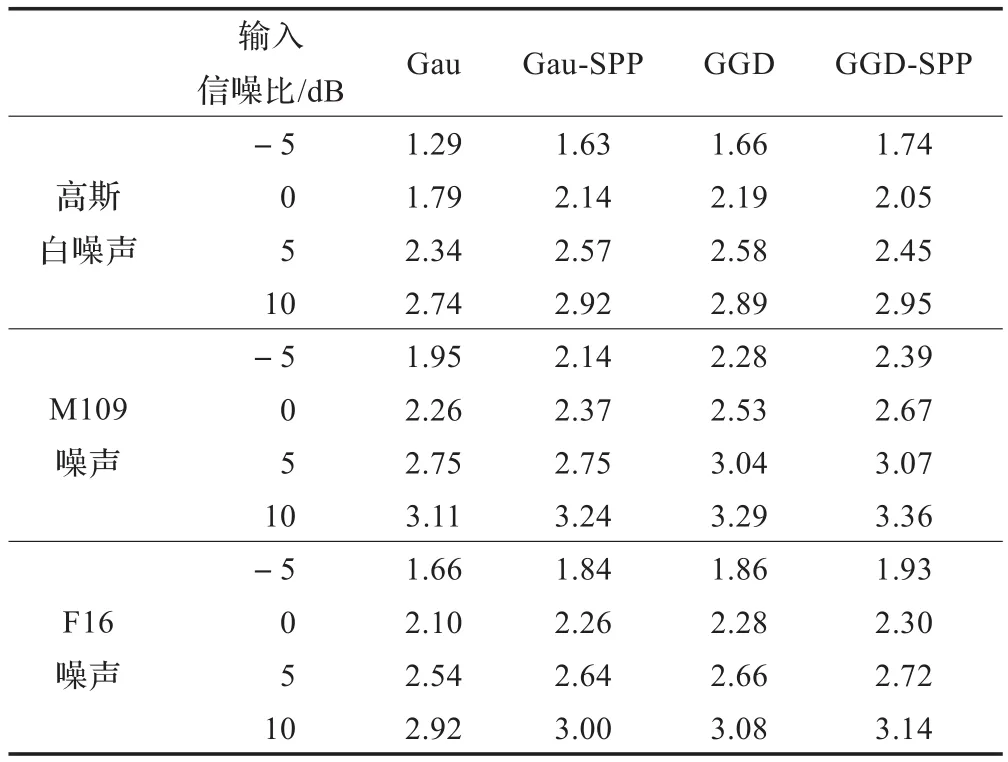
表2 四种算法PESQ评估得分
采用平均意见得分(Mean Opinion Score,MOS)对本文提出算法的增强语音的主观感知质量进行评估,语音的失真级别,质量等级与对应的MOS打分情况如表3所示。
选取实验室内的12名研究生学员作为参评人员,对本文提出算法的增强语音进行评估,在接听者听完被测语音后,从表3中的5个等级中选取一项作为对测听语音的评价,然后,对全部参选人员的评估结果取平均值,得到测试语音的最终MOS得分。如表4。

表3 MOS打分等级
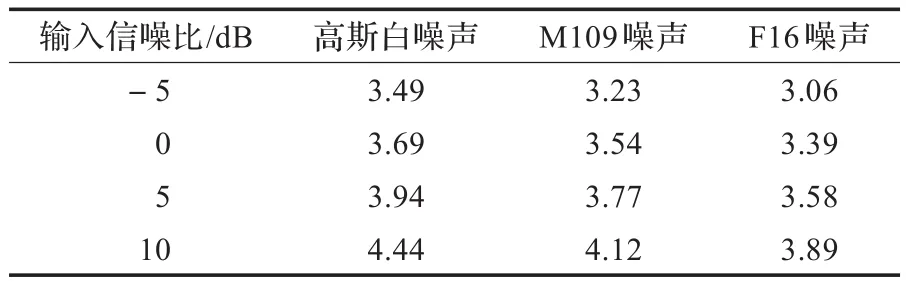
表4 本文算法的MOS得分
从表4可以看出本文提出算法的增强语音在三种环境噪声下,信噪比较高时增强语音的主观感知质量比较好,几乎没有不适感;信噪比较低时增强语音的主观感知质量虽有所下降,但其仍具有较高可懂度。主观评估结果与客观评估结果基本一致,达到了预期的增强效果。
图2分别给出了原始语音,以及信噪比为0 dB的F16战斗机噪声环境下的带噪语音和四种增强算法的(Gau、Gau-SPP、GGD、GGD-SPP)增强语音的时域波形图和语谱图。从图中可以看出,与其他三种算法相较,本文提出的新的基于广义Gamma语音模型的短时谱估计算法的增强语音的残留噪声较少,并且谱失真度较小,并且能够更好地抑制音乐噪声,提高增强语音质量。
6 结束语
本文提出了一种新的基于广义Gamma语音模型的对数谱估计语音增强算法。在假设语音信号幅度谱服从广义Gamma分布的基础上,不仅推导了语音对数谱的MMSE估计式,而且进一步推导了在该模型假设下的语音存在概率对MMSE估计进行修正。与传统的短时谱估计语音增强算法相比,本文提出的算法不仅能进一步提高增强语音的信噪比,而且可以有效地提高增强语音的感知质量,抑制残留噪声。另外,本文引入语音存在概率修正因子,实际上相当于对语音信号短时谱估计的一种二状态扩展,考虑到不同语音信号频谱分布特性的差异,可以将其进一步扩展至多种状态[13],将在下一步的工作中对此展开研究。
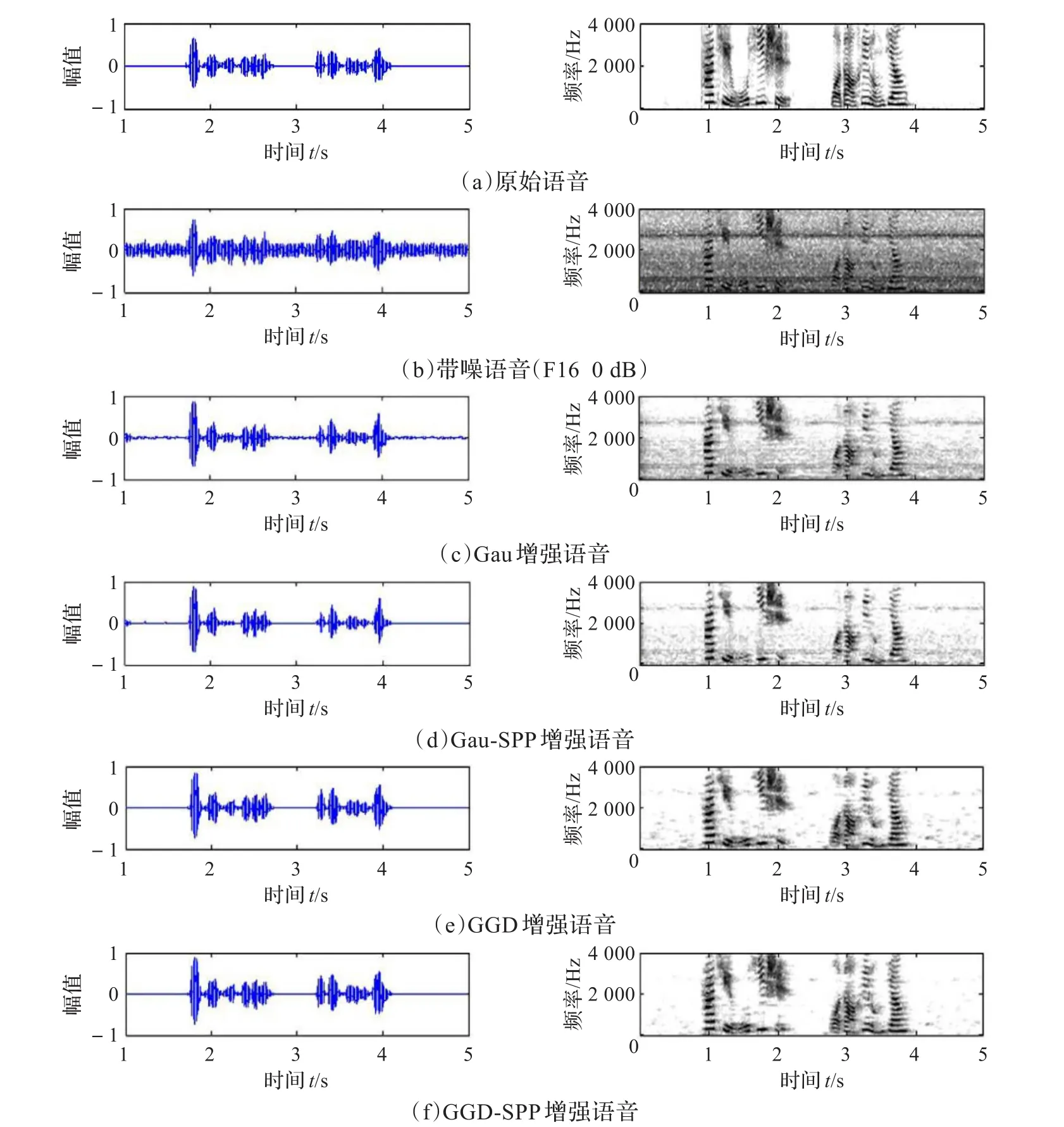
图2 语谱图和时域波形图
[1]Ephraim Y,Malah D.Speech enhancement using a minimum mean-square error short-time spectral amplitude estimator[J].IEEE Trans on Acoust Speech,Signal Process,1984,32(6):1109-1121.
[2]Ephraim Y,Malah D.Speech enhancement using a minimum mean-square error log-spectral amplitude estimator[J].IEEE Trans on Acoust Speech,Signal Process,1985,33(2):443-445.
[3]Cohen I.Optimal speech enhancement under signal presence uncertainty using log-spectral amplitude estimator[J].IEEE Signal Process Lett,2002,9(4).
[4]Gazor S,Zhang W.Speech probability distribution[J].IEEE Signal Process Lett,2003,10(7).
[5]Martin R.Speech enhancement based on minimum meansquare error estimation and super gaussian priors[J].IEEE Trans on Speech Audio Process,2005,13(5):845-856.
[6]Lotter T,Vary P.Speech enhancement by MAP spectral amplitude estimation using a super-Gaussian speech model[J].Eurasip J Signal Process,2005(7):1110-1126.
[7]邹霞,陈亮,张雄伟.一种基于Gamma语音模型的语音增强算法[J].通信学报,2006,27(10):118-123.
[8]Erkelens J S,Hendriks R C,Heusdens R,et al.Minimum mean-square error estimation of discrete flourier coefficients with generalized Gamma priors[J].IEEE Trans on Audio,Speech,Language Process,2007,15(6):1741-1752.
[9]Borgstrom B J,Alwan A.Log-spectral amplitude estimation with generalized Gamma distributions for speech enhancement[C]//IEEE Int Conf Acoustic,Speech,Signal Process(ICASSP),Prague,Czech,2011:4756-4759.
[10]Thomas E,Peter V.Model-based speech enhancement using SNR dependent MMSE estimation[C]//IEEE Int Conf Acoustic,Speech,Signal Process(ICASSP),Prague,Czech,2011:4652-4655.
[11]Gradshteyn I S,Ryzhik Z M.Table of integrals,series,and products[M].New York:Academic Press,1980.
[12]Martin R.Noise power spectral density estimation based on optimal smoothing and minimum statistics[J].IEEE Transactions on Speech and Audio Processing,2001,9(5).
[13]Ephraim Y.A Bayesian estimation approach for speech enhancement using Hidden Markov Models[J].IEEE Transactions on Signal Processing,1992,40(4).

