基于单演同相幅值模式的人脸识别方法

刘机福，王炼红，汤春龙

LIU Jifu,WANG Lianhong,TANG Chunlong

湖南大学 电气与信息工程学院，长沙 410082

College of Electrical and Information Engineering,Hunan University,Changsha 410082,China

1 引言

近年来，人脸识别逐渐成为模式识别和计算机视觉领域的研究热点，在视频监控及数字安防等方面有着十分广泛的应用前景。Gabor小波由于对外界变化具有鲁棒性的特征，在人脸识别中得到了广泛的应用[1]，但是Gabor小波特征的维数往往较高，这使得基于Gabor变换的方法往往具有较大的复杂度[2]。针对这一问题，Yang[3]等人将单演信号理论引入到人脸识别中，运用图像的单演幅度和方向信息进行人脸识别并获得了极好的效果。实验表明基于单演滤波的方法的识别性能与基于Gabor变换的方法基本相当甚至超过了基于Gabor的方法。同时基于单演滤波的方法能够极大地降低算法的时间复杂度和空间复杂度。但是文献[3]中的编码方式却未对单演滤波产生的相位信息加以利用，单演信号具有稳定的局部几何特征和局部相位定位能力，基于单演相位的边缘识别精度甚至能达到亚像素级别。因此，文献[4-5]中利用单演相位进行光流估计。而本文提出了一种新颖的特征提取方法——单演同相幅值模式。考虑到提取的高维特征中往往包含较多的冗余信息，本文进一步采用基于分块的线性判别方法对提取的特征（Block-based Fisher Linear Discrimination，BFLD）[6]进行降维，以获得最具判别能力的特征。该算法先用PMMSP算子提取图像的特征，再运用BFLD对特征进行降维，充分利用了相位和幅值信息，提高了系统的识别性能。

2 基于单演同相幅值模式的人脸表示

2.1 单演信号理论

单演信号[7]是一维解析信号的2D扩展。单演图像表述法通过使用单演滤波器对图像进行滤波，获取图像局部幅值、相位和方向信息来得出给定图像结构信息的二维解析表述。近年来，单演信号分析在纹理分析、图像降噪以及立体匹配等图像处理领域得到了广泛的应用。

设图像为 f(x，y)，x、y表示二维图像域的坐标。在单演信号里2D带通信号可以通过Log-Gabor滤波器g(x，y)产生。然后通过Riesz变换来获取图像的单演信号表述。Riesz变换在频域内表达式为[Hu(u,v)，Hv(u,v)]，hx(x，y)，i=x，y为对应的空间域表示。则单演信号可以表示为：

fM(x，y)=g(x，y)*f(x，y)*[1，hx(x，y)，hy(x，y)] （1）

其中“ *”表示卷积运算。 g(x，y)=F-1(G(ω))，F-1表示傅里叶逆变换。G(ω)为Log-Gabor滤波器的频域表示。其表达式如式（2）所示：

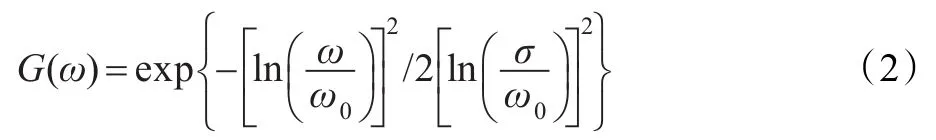
其中δ为带宽比例因子，ω0为中心频率。

则图像 f(x，y)的单演幅值 M 、单演方向θ和单演相位P可以分别表示为：

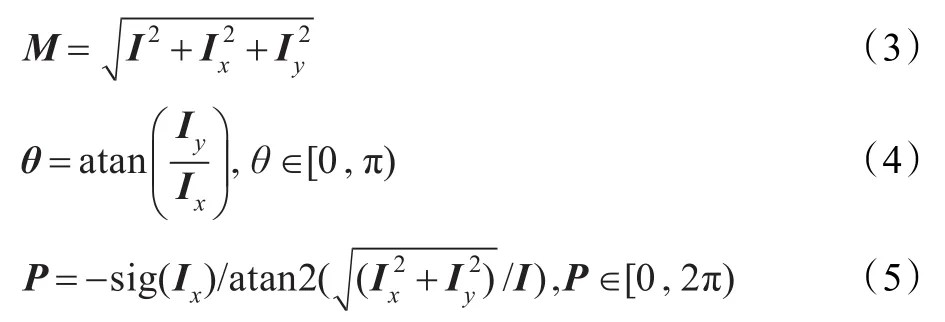
其中

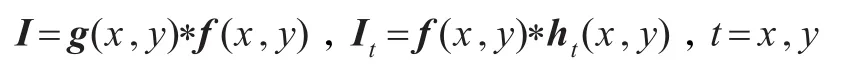
单演滤波的尺度空间由Log-Gabor滤波器的尺度因子S来定义。

其中：λmin为最小波长，μ为波长的倍增系数。

2.2 单演同相幅值模式

不同于边缘轮廓信息，单演相位特征包含了图像的绝大部分重要特征信息，只需知道单演相位信息就能重建原图像[8]。而且单演相位特征最大的优点是完全独立于亮度信息，不受光照变化的影响，而且该特征具有很好的抗噪声性能。单演幅度则包含着图像的能量信息，因而从图像的单演幅度和相位图中可以获得有效的识别信息。

文献[9-10]中提出了一种针对梯度方向和幅度的方向边缘幅值方法并且取得了很好的效果。受其启发，本文对单演特征中的幅度和相位信息进行与之相似的处理，从而获得单演同相幅值模式。

首先，由于相位对图像的局部位置变化极为敏感，因此为了增强编码的鲁棒性，本文并不关心具体的相位角度，而是关注每个像素点的相位所处的区间。与文献[11]类似，本文算法中也将相位根据其角度大小划分为4个区间，即[0°，90°），[90°，180°），[180°，270°），[270°，360°）。然后，对于图像中的任一像素点 pc，以 pc为中心在一个矩形区域（本文称为“单元”）内对相位处于同一区间的像素点的幅值进行累加。最后再以 pc为中心在一个圆形区域（本文称为“块”）内对处于同一相位区间的累加后的幅值进行二值编码。所以，单演同相幅值模式编码的数学表达式为：

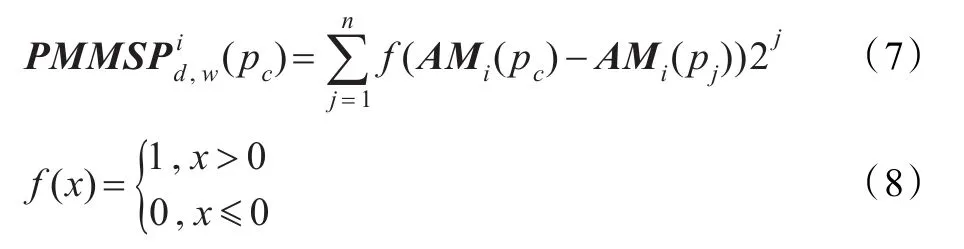
其中，i(i=1、2、3、4)表示第i个相位区间。 d表示二值编码圆形采样“块”的直径，w表示“单元”大小。AMi(pc)表示像素点 pc在第i个相位区间内的幅度累加值。ΑΜi(pj)表示第i个区间内的像素点 pc的第 j个邻域（即像素点 pj在以自己为中心的一个单元内的幅度累加值）。n表示中心像素点 pc的邻域采样点个数。则在 pc点的PMMSP特征可表示为4个相位区间相对应的PMMSP集合，如式（9）所示：

图1以6点采样(n=6)为例说明了PMMSP算子对pc点进行特征提取的过程。图1中的每一个方块即为一个“单元”，以 pc为中心的环形区域即为一个“块”。

将图像的每一个像素点按照上述方式编码为4个不同相位区间的PMMSP编码值，然后分别按照不同相位区间将每个像素点的PMMSP值分解，则可以得到4张对应于不同相位区间的PMMSP模式图。然后将每张PMMSP图分块并分别统计每一块的直方图。最后将同一张图片的所有PMMSP模式图的直方图串联得到最终的特征向量。本文固定采用3种尺度的单演滤波器，则一张人脸图像可以分解为12张PMMSP模式图。

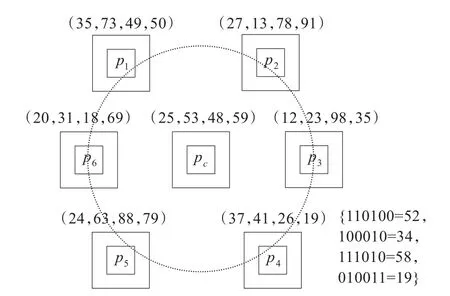
图1 PMMSP算子示意图

3 基于分块的线性判别分析（BFLD）

FLD主要是通过最小化类内散度最大化类间散度来达到最佳的分类效果[12-13]。在线性假设的前提下，FLD通过最大化样本类间散布矩阵和类内散布矩阵的比值达到求解最佳投影矩阵的目的，即

其中，x为训练样本，mi是Ci类的均值，m是所有样本的均值。对于式（10），可通过求解广义特征值问题SBW=SWWΛ来获得最优的解空间。

传统的FLD都是抽取图像的全局特征，而实际上在光照、表情尤其是遮挡环境中往往出现人脸部分区域变化较大而其他部分变化不大的情况，而此时若直接对整体特征运用FLD投影将造成较大的误差。文献[14]指出：全局非线性数据结构可以被看成是局部线性的，且局部结构可以被线性拟合。因而可以将图像分为若干个块，分别对每个块的特征独立进行FLD投影，然后将每个块的投影特征重新组合成全局特征进行目标匹配。这样通过对每个局部块进行线性判别分析，尽可能地逼近人脸图像的真实分布，减小图像局部变化对算法整体性能的影响。同时，采用分块策略可以有效地避免因样本特征维数过高导致的“小样本问题”，可谓一举多得。

4 结合PMMSP和BFLD的人脸识别

首先利用PMMSP方法获得人脸图像的有效特征，然后用BFLD进行特征映射，这样不仅可以有效地降低特征维数，而且显著提高PMMSP特征的识别能力。具体的BFLD降维过程如下：

（1）将由式（7）得到的编码图像分为 K块（下文称之为母块），然后将每个母块分为N个子块，并求取各子块的直方图特征，最后按照一定的规律串接成表示该母块特征的特征向量。

（3）如果直接应用Fisher线性判别求取最佳投影矩阵，由于特征维度过高，往往会出现小样本问题。尽管本文采用了分块方式能够适当降低特征维度，但是为了避免在Fisher中出现小样本问题，拟应先用PCA对特征进行降维。因此，在训练集中，对步骤2得到的Hi应用PCA进行降维，在PCA降维后的特征空间中，求解公式（10），即计算使得类间散度和类内散度比值最大的投影向量（Fisher最佳投影向量），从而形成最佳投影向量矩阵Wi。

（4）对于注册集和测试集，由步骤1，2得到原始低维特征集合和，并通过步骤3得到的Wi线性投影到低维判别空间中，形成低维特征和，即Fi=

本文用余弦距离来衡量两个母块间的相似度，并将M个母块的相似度累加作为最终两张图片间的相似度。其计算公式如下所示：

其中S(IG，IP)表示注册图像 IG和测试图像IP之间的相似度。

5 实验结果及分析

本实验在Windows XP，Matlab7.0平台下实现，运行环境是Intel双核处理器，2 GB内存，人脸库采用中科院CAS-PEAL人脸库和AR人脸库。

5.1 在CAS-PEAL人脸数据库上的实验

CAS-PEAL人脸数据库中包含1 040名中国人共99 450幅头肩部图像。所有图像在专门的采集环境中采集，涵盖了姿态、表情、饰物、背景、时间和光照6种主要变化条件。本文实验主要在表情、饰物和光照3个子库上进行，由于库中原图像较大，实验中将所有图片均以其眼睛坐标为基准按照一定的规格裁剪为100×100大小。

首先探讨本文方法中参数对识别率的影响，其中对识别率影响较大的两个参数是PMMSP算子中的“单元”和“块”的大小。因而从CAS-PEAL的表情、饰物和光照3个子集中分别随机选200张共计600张图片组成测试集。在固定图像分块方式为8×8（64块）的情况下，令PMMSP算子中w（即单元大小为w像素×w像素）分别取3、4、5、6、7、8、9、10、11以及 d（PMMSP算子中圆形块的直径）分别取3、4、5、6、7、8、9、10、11时测试了每种参数组合的识别率，并绘制了识别率的三维柱形图，各种组合下的识别率如图2所示。其中单演滤波器的参数设置为：S=3，λmin=4，μ=1.8，δ/ω0=0.64。

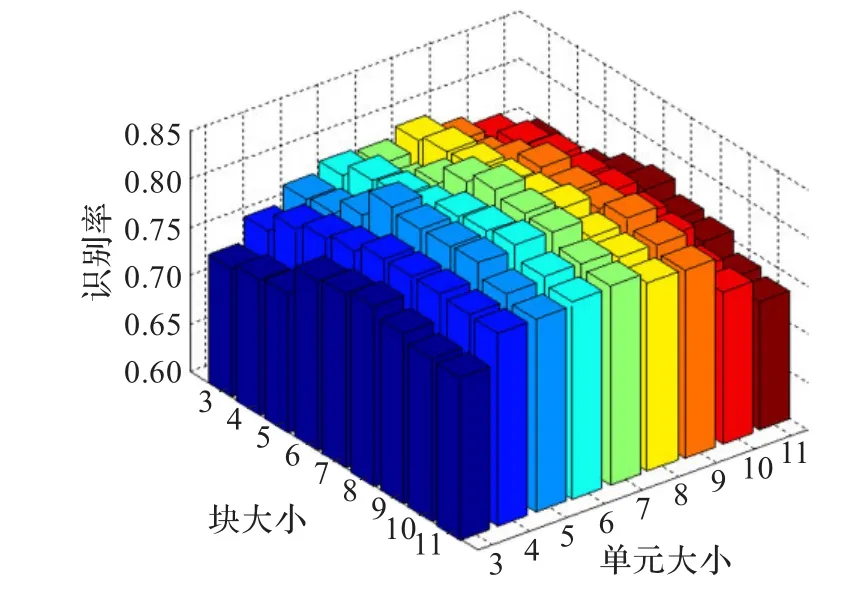
图2 不同块和单元大小时的识别率

由图2可知，PMMSP算子中的块和单元过大或者过小对识别率都会造成一定的影响。当单元大小w和块的直径d均取7的时候取得最佳识别效果，这主要是因为，当w和d取值过大的时候，虽能把握区域的变化趋势，但会导致微小局部信息的丢失，不能准确把握微小局部相位信息的变化。而当w和d取值过小，虽然能够准确提取相位的微小局部变化信息，但是却导致对更大的区域相位信息的把握不足，不能有效提取区域性的区域信息。而当w，d分别取值7的时候，该算法恰好能够同时兼顾微小局部信息和区域变化信息。图2的实验数据也充分表明，只有当w和d都取值恰当的时候，本文算法才能达到最好的性能。因此本文余下实验中均固定参数w=7，d=7。

为了测试本文算法的识别性能，在CAS-PEAL表情、饰物及光照3个子集上分别进行了实验。实验中单演滤波器参数与前文设置相同。为了进行对比，本文同时测试了MBP算法在3个子集上的识别率和几种算法的综合识别率（MBP中单演滤波器参数与PMMSP中设置完全相同，MBP算子中对幅值采样时采用半径为3的8点采样）。另外文中列举了文献[15]中运用LBP和LGBP算法在这3个子集上所取得的最佳识别率。其中PMMSP+BFLD（下文中以PMMSP_F表示）和MBP+BFLD（下文中以MBP_F表示）算法中，每幅图片分成4×4个母块，每个母块分成2×2个小块。本文BFLD方法中每个块的直方图特征经过PCA降维后均保留C-1维（C为训练样本类别数）。各种方法在CAS-PEAL人脸数据库表情、饰物以及光照三个子集上识别率及相应的特征长度如表1所示。

表1 不同算法在CAS-PEAL人脸库识别率

在CAS-PEAL人脸库上的实验结果表明：本文所提出的PMMSP特征提取算法在不经过BFLD训练的情况下，已经取得了较好的识别率。在表情和饰物两个子集上的识别率与MBP持平，甚至优于MBP，说明了本文提出的PMMSP算法能够有效提取图像的判别特征。而在光照子集上的识别率则明显高于MBP，说明本文算法对图像光照变化具有较好的鲁棒性。在经过BFLD训练之后，各个子集上的识别率均有了不同程度的提升，这主要得益于BFLD能够有效提取判别特征，压缩冗余信息，逼近人脸的真实分布，克服了全局特征不能有效描述局部人脸变化的缺点。而且由表中各种算法的综合识别率可以看出，本文算法的综合识别率是几种算法中最高的，说明了本文提出的将PMMSP与BFLD相结合的方法的有效性。

同时，为了对比各种算法的复杂度，以CAS-PEAL光照子集作为测试集，在每种方法均采取8×8分块的策略下，测试了每种方法对光照子集完成一次测试每幅样本所耗费的平均时间。各种方法在8×8分块时的特征长度以及每幅图片所需的平均时间如表2所示。

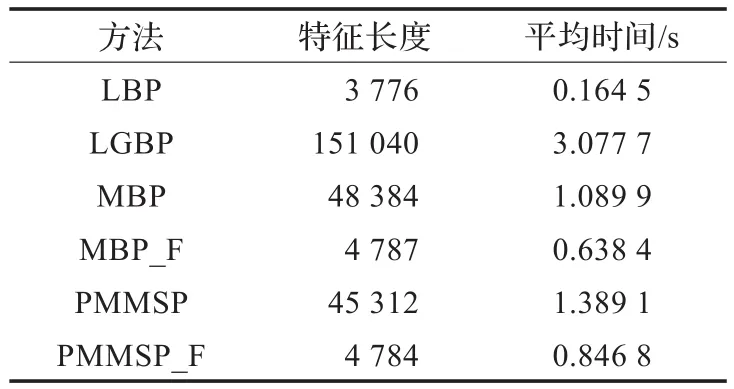
表2 相同分块方式下各算法特征长度及平均时间

由表2可以看出，在分块方式相同的情况下，本文算法的特征长度不仅远小于LGBP而且也小于MBP方法，同时由各种算法所耗费的平均时间可以看出，本文方法虽然比MBP相比所耗费时间稍多，但由上述分析知道，本文方法在识别率上是有较大优势的。根据文献[11]，在进行单演滤波时，只需要3次卷积运算和6次Riesz变换，相对于LGBP的40次卷积运算可大大降低算法的时间复杂度，而且本文方法最终仅产生12幅模式图，同样远远小于LGBP算法的40幅模式图。与传统的LGBP相比，PMMSP的空间复杂度仅为LGBP的1/4，时间复杂度仅为其的1/3。相对MBP而言，虽然PMMSP算法最终产生的模式图数目比MBP多，但是由于PMMSP模式数目远小于MBP模式数目，因而最终提取的PMMSP特征长度仍小于MBP算法，这样将有效降低算法运算过程中所需的存储空间，降低空间复杂度。PMMSP_F在PMMSP上进一步采用BFLD降维，虽然BFLD需要进行额外的训练获取最佳投影矩阵，而且训练复杂度也较大，但是，本文所述的BFLD采用的是离线训练的方式，其对在线识别的影响仅仅是多做了若干次线性映射，因此在时空复杂度方面，其对算法识别的影响是十分有限的。从表2的实验数据可以看出，PMMSP_P特征长度仅为PMMSP的1/9，同时相对MBP，LGBP等都大为降低，同时表2的经验时间表明PMMSP_F的时间复杂度也较MBP，LGBP，PMMSP小。所以可以看出，本文提出的PMMSP和PMMSP_F方法不单在识别率上具有优势，而且能够有效降低时间和空间的消耗。

5.2 在AR人脸数据库上的实验

AR人脸库共包括来自126人分两批次采集的超过4 000幅正面人脸图像。该人脸库包含了光照、表情和遮挡的变化子集。在本文实验中，在126人中选出50个男性对象和50个女性对象共100人的2 600张图片组成数据库子集进行测试，且实验前所有图像均裁剪到165像素×120像素大小。测试集共分为四种，第一种是无遮挡情况下的识别率，第二种遮挡物为墨镜，第三种遮挡为围巾，第四种为总的识别率。对于无遮挡的情况，取第一批次下的每人无遮挡的7张图片共计700张作为注册集，第二批次下的每个人无遮挡的7张图片作为测试集合。对于有遮挡的测试，只选用第一批次下每个对象的第一张图片作为注册集，两个批次下所有墨镜遮挡的图片和两个批次下所有有围巾遮挡的图片分别组成两个测试集。在BFLD训练阶段，取第一批次下无遮挡的7张图片作为训练集。文献[3]中在AR人脸库上的测试与本文实验设置完全相同，因而本文列举了文献[3]中LBP和LGBP两种算法在AR人脸库上的识别率。对于MBP和PMMSP则采用完全相同的单演滤波器参数，且分块方式与文献[3]中相同均为8×8分块。BFLD训练阶段每张图分为4×4个母块，每个母块进一步分为2×2个子块。各种算法识别率如表3所示。

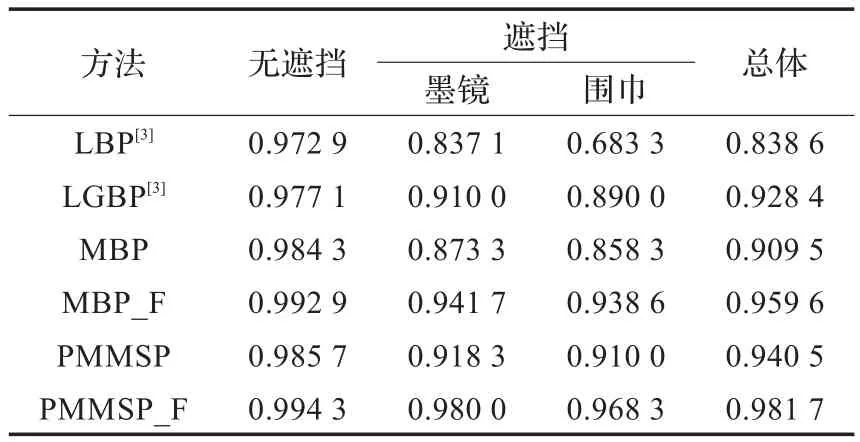
表3 各种算法在AR人脸库的识别率

由表3可以看出，本文方法在AR人脸库上表现出了极好的识别性能，本文算法在墨镜遮挡和围巾遮挡的情况下识别率均高于MBP算法，同时也高于LGBP方法，说明本文提出的PMMSP算子对于遮挡也具有一定的鲁棒性。另外，PMMSP特征经过BFLD方法投影后进一步提高了识别率，即便是在遮挡面积较大的两个测试集合上同样取得了较高的识别率，PMMSP_F算法在AR人脸库上的综合识别率仍然是所列算法里最高的，充分说明了本文算法的有效性。

6 结束语

本文研究了单演信号理论在人脸识别中的应用。为了提取图像的有效分类特征，提出了一种新的算子-单演同相幅值模式来提取图像单演滤波后产生的单演幅度和单眼相位图中的信息。同时为了降低算法的复杂度，本文进一步提出了将PMMSP与BFLD相结合的人脸识别方法。在CAS-PEAL和AR人脸库上的实验证明了本文算法的有效性。如何从图像单演滤波后产生的多模式单演特征中获得更具有分辨力的特征是下一步的研究重点。

[1]Zhang Wenchao，Shan Shiguang.Local Gabor Binary Pattern Histogram Sequence（LGBPHS）：a novel non-statistical model for face representation and recognition[C]//Proceedings of 5th International Conference on Computer Vision，Beijing，China，2005：786-791.

[2]徐永红，侯景，赵艳茹，等.Gabor小波幅值和相位特征人脸识别方法比较[J].计算机工程与应用，2012，48（15）：195-200.

[3]Yang Meng，Zhang Lei，Zhang Lin，et al.Monogenic Binary Pattern（MBP）：a novel feature extraction and representation model for face recognition[C]//20th IEEE International Conference on Pattern Recognition，2010：2680-2683.

[4]Felsberg M.Optical flow estimation from monogenic phase[C]//Complex Motion.Berlin Heidelberg：Springer，2007：1-13.

[5]Alessandrini M，Bernard O，Basarab A，et al.Multiscale optical flow computation from the monogenic signal[J].IRBM，2013，34（1）：33-37.

[6]Xie Shufu，Shan Shiguang，Chen Xilin，et al.Fusing local patterns of gabor magnitude and phase for face recognition[J].IEEE Transactions on Image Processing，2010，19（5）：1349-1361.

[7]Felsber G M，Sommer G.The monogenic signal[J].IEEE Transactions on Signal Processing，2001，49（12）：3136-3144.

[8]Zang D，Sommer G.Phase based image reconstruction in the monogenic scale space[C]//Pattern Recognition.Berlin Heidelberg：Springer，2004：171-178.

[9]Vu N S，Caplier A.Face recognition with patterns of oriented edge magnitudes[C]//Computer Vision-ECCV 2010.Berlin Heidelberg：Springer，2010：313-326.

[10]Vu N S.Exploring patterns of gradient orientations and magnitudes for face recognition[J].IEEE Transactions on Information Forensics and Security，2013，8（2）：295-304.

[11]Yang Meng，Zhang Lei.Monogenic binary coding：an efficient local feature extraction approach to face recognition[J].IEEE Transactions on Information and Security，2012，7（6）：1738-1751.

[12]Sanguansat P，Adornwised W，Jitaponkul S，et al.Two-dimensional linear discriminant analysis of principle component vectors for face recognition[C]//IEEE Int Conf on ICASSP.Washington DC：IEEE Computer Society，2006：345-348.

[13]戴文战，周昌亮.一种改进Fisher准则的线性判别分析方法[J].计算机工程与应用，2013，49（3）：210-212.

[14]Roweis S T，Saul L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science，2000，290（5500）：2323-2326.

[15]张文超.局部Gabor二值模式人脸表示与识别方法研究[D].哈尔滨：哈尔滨工业大学，2007.